تستعرض هذه المقالة أربعةً من خوارزميات الأشجار والمخططات، وهي خوارزمية البحث بالعرض أولا BFS، وخوارزمية البحث بالعمق أولا DFS، والبائع المتجول، وخوارزمية كثيرة الحدود للعثور على أصغر غطاء رأسي في مخطط ما.
البحث بالعرض أولا Breadth-First Search
سنحاول استعمال هذه الخوارزمية في عدة تطبيقات عمليات بحث.
البحث عن أقصر مسار من المصدر إلى العقد الأخرى
خوارزمية البحث بالعرض أولا BFS هي خوارزمية لتسلق مخطط أو البحث فيها. تبدأ الخوارزمية من جذر الشجرة (أو أيّ عقدة من المخطط، ويُشار إليها أحيانًا باسم "مفتاح البحث" - search key)، ثمّ تستكشف العقد المجاورة أولاً قبل الانتقال إلى المستوى التالي من العقد.
اكتُشفت خوارزمية BFS في أواخر الخمسينيات من قبل إدوارد فورست مور Edward Forrest Moore، الذي استخدمها للعثور على أقصر مسار للخروج من متاهة، وقد اكتُشفت أيضًا بشكل مستقل من قبل CY Lee الذي استخدمها في مجال التوجيه السلكي في عام 1961.
تفترض خوارزمية BFS الأمور التالية:
- لن نجتاز أي عقدة أكثر من مرة.
- تقع العقدة المصدرية (أي العقدة التي نبدأ منها) في المستوى 0.
- العقد التي يمكننا الوصول إليها مباشرة من العقدة المصدرية ستكون في المستوى 1، والعقد التي يمكننا الوصول إليها مباشرة من عقد المستوى 1 ستكون في المستوى 2 وهكذا دواليك.
- يشير مستوى عقدة ما إلى أقصر مسار يصل إلى تلك العقدة انطلاقًا من المصدر.
انظر المثال التالي:
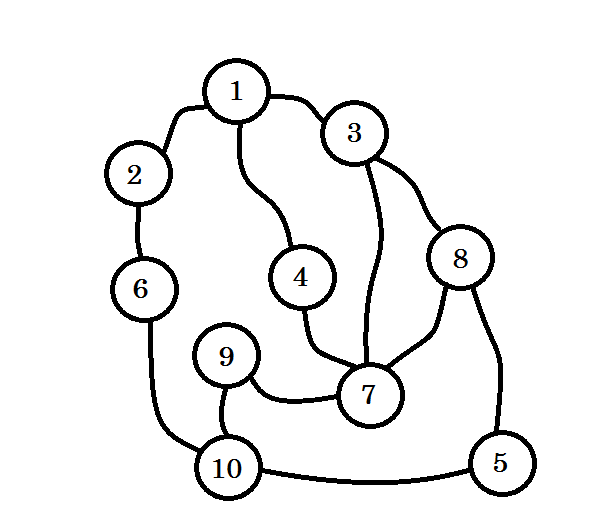
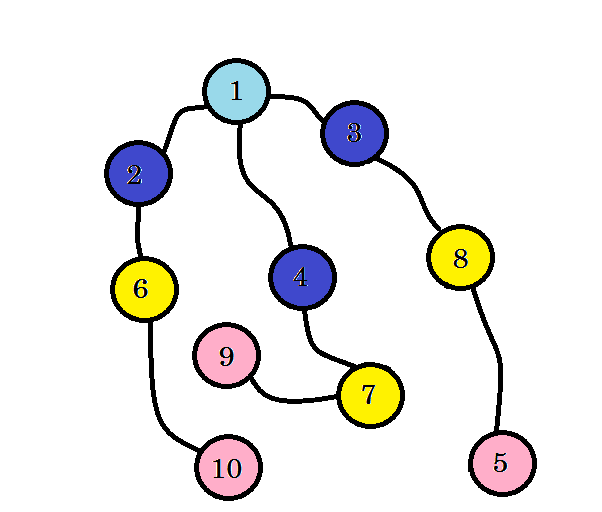
لنفترض أنّ هذا المخطط يمثل طرقا بين عدة مدن حيث تمثل كل عقدة مدينة واحدة، فيما يشير كل ضلع بين عقدتين إلى طريق يربط بينهما، ونحن نريد الانتقال من العقدة 1 إلى العقدة 10. ستكون العقدة 1 هي المصدر، وهذا يجعلها في المستوى 0. نحدد (نلوّن) العقدة 1 لنشير إلى أننا زرناها.
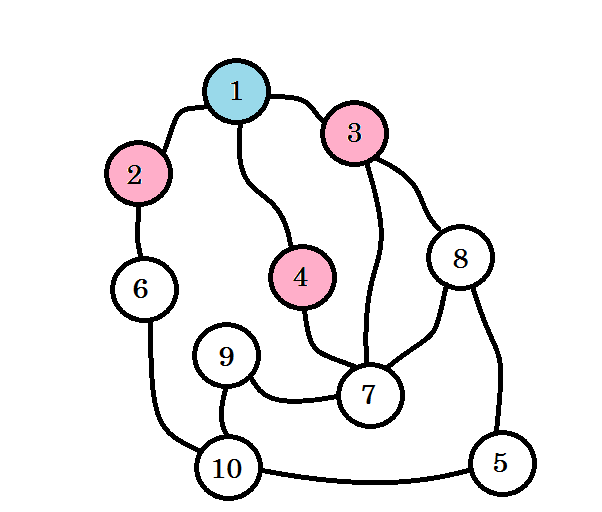
يمكننا الذهاب إلى العقدة 2 أو العقدة 3 أو العقدة 4 من العقدة المصدر، أي العقدة 1، لذلك ستكون هناك 3 عقد من المستوى 1. نحدد هذه العقد لنبيّن أنّها مُزارة، ثمّ نعمل عليها.
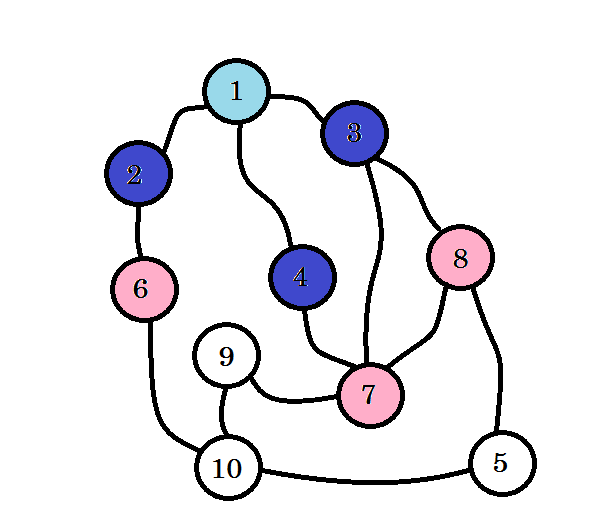
نلوّن العقد المُزارة، حيث نلوّن العقد التي نعمل عليها حاليًا باللون الوردي، تذكّر أنّنا لن نزور العقدة نفسها مرتين. يمكننا الذهاب إلى العقد 6 و 7 و 8 عبر كل من العقدة 2 والعقدة 3 والعقدة 4، وسنحددهذه العقد لنبيّن أنّها مُزارة. مستوى هذه العقد سيساوي (1 +1) = 2.
يشير مستوى العقد إلى أقصر مسافة بينها وبين المصدر. على سبيل المثال: بما أن العقدة 8 موجودة في المستوى 2، فهذا يعني أنّ المسافة من المصدر إلى العقدة 8 هي 2.
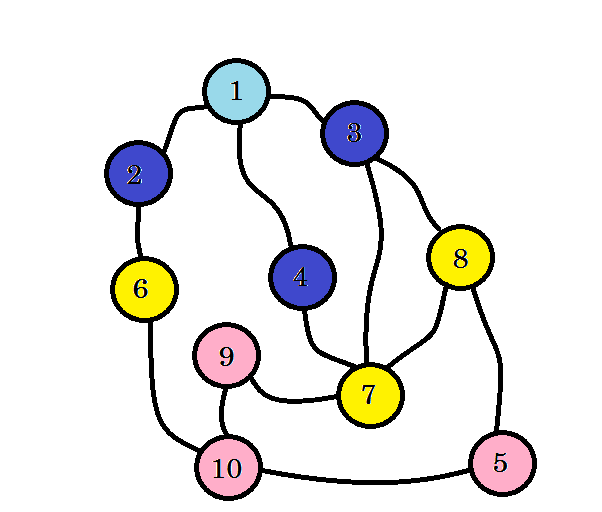
لم نصل بعدُ إلى العقدة المستهدفة وهي العقدة 10، لذا ننتقل إلى العقد التالية. نستطيع الانطلاق من أيّ من عقد المستوى 2، وهي العقدة 6 والعقدة 7 والعقدة 8.
ها قد وجدنا العقدة 10 عند المستوى 3، هذا يعني أنّ أقصر مسار من المصدر إلى العقدة 10 هو 3، وقد بحثنا في كل مستوى من مستويات المخطط إلى أن وجدنا أقصر مسار، وإذ ذاك سنمسح الأضلاع التي لم نستخدمها:
بعد إزالة تلك الأضلاع التي لم نستخدمها نحصل على شجرة تُسمى شجرة البحث بالعرض أولًا BFS. تُظهر هذه الشجرة أقصر مسار من المصدر إلى جميع العقد الأخرى.
مهمتنا الآن هي الانتقال من العقدة المصدر إلى العقد الموجودة في المستوى 1، ثم من عقد المستوى 1 إلى عقد المستوى 2، وهكذا حتى نصل إلى وجهتنا. يمكننا استخدام الطوابير Queues لتخزين العقد التي سنعالجها. لكل عقدة نعمل عليها فإننا ندفع (نضيف) إلى الطابور جميع العُقد الأخرى التي من الممكن اجتيَازها مباشرة لكنّنا لم نفعل بعد.
هذه محاكاة للمثال:
أولاً، ندفع العقدة المصدر إلى الطابور، فيبدو هكذا:
front +-----+ | 1 | +-----+
مستوى العقدة 1 يساوي 0، أي level[1] = 0، نبدأ الآن البحث بالعرض أولا BFS.
في البداية، ننزع عقدة من الطابور فنحصل على العقدة 1، يمكننا -انطلاقًا من هذه العقدة- أن نذهب إلى العقدة 4 أو 3 أو 2، لهذا فهذه العقد الثلاث من المستوى الأول، أي level[4] = level[3] = level[2] = level[1] + 1 = 1. سنحددالآن هذه العقد لنبيّن أنّها مُزارَة، ثمّ ندفعها إلى الطابور.
front +-----+ +-----+ +-----+ | 2 | | 3 | | 4 | +-----+ +-----+ +-----+
ننزع الآن العقدة 4 من الطابور ونعالجها، نستطيع الذهاب منها إلى العقدة 7، لهذا يكون لدينا: level[7] = level[4] + 1 = 2. والآن نحددالعقدة 7، ثمّ ندفعها إلى الطابور.
front
+-----+ +-----+ +-----+
| 7 | | 2 | | 3 |
+-----+ +-----+ +-----+
من العقدة 3، يمكننا الذهاب إلى العقدة 7 أو العقدة 8، وبما أن العقدة 7 محددة من قبل (أي مُزارة سابقًا)، فإننا نحدد العقدة 8، ونضع level[8] = level[3] + 1 = 2. والآن ندفع العقدة 8 إلى الطابور.
front +-----+ +-----+ +-----+ | 6 | | 7 | | 2 | +-----+ +-----+ +-----+
ستستمر هذه العملية حتى نصل إلى وجهتنا أو نُفرِغ الطابور، وتزوّدنا مصفوفة المستويات level بطول أقصر مسار من المصدر. نستطيع تهيئة عناصر مصفوفة المستويات بقيمة اللانهاية، كناية إلى أنّ العقد لم تُزر بعد.
انظر المثال التوضيحي لهذا:
Procedure BFS(Graph, source): Q = queue(); level[] = infinity level[source] := 0 Q.push(source) while Q is not empty u -> Q.pop() for all edges from u to v in Adjacency list if level[v] == infinity level[v] := level[u] + 1 Q.push(v) end if end for end while Return level
يمكننا معرفة المسافة التي تفصل كل عقدة عن المصدر من خلال التكرار عبر مصفوفة المستويات، على سبيل المثال: المسافة إلى العقدة 10 من المصدر مخزّنة في level[10].
قد نريد أحيانًا أن نعرف المسارات الأخرى التي يمكن أن تُوصلنا إلى العقدة انطلاقًا من المصدر، وذلك إلى جانب المسار الأقصر. لفعل هذا نحتاج إلى مصفوفة جديدة نسميها parent، قيمة parent[source] (source هنا تعني العقدة المصدر) ستكون معدومة NULL. نضيف التعليمة parent[v] := u إلى المثال الوهمي عند كل تحديث لمصفوفة المستويات level في حلقة for.
لكي تعثر على المسار بعد انتهاء خوارزمية البحث العرضي أولًا، يكفي أن تجتاز المصفوفة parent خلفيًا إلى أن تصل إلى المصدر، والذي يحمل القيمة NULL في هذه المصفوفة.
هذا مثال توضيحي يستخدم العودية recursion:
Procedure PrintPath(u): if parent[u] is not equal to null PrintPath(parent[u]) end if print -> u
وهذا مثال لا يستخدمها وإنما يستخدم التكرارية فقط iteration:
Procedure PrintPath(u): S = Stack() while parent[u] is not equal to null S.push(u) u := parent[u] end while while S is not empty print -> S.pop end while
تعقيد الخوارزمية: سوف نزور كل عقدة وكل ضلع مرّة واحدة بالضبط، لذا سيكون تعقيد الخوارزمية الزمني O (V + E)، حيث يمثل V عدد العقد، ويمثّل E عدد الأضلاع.
البحث عن أقصر مسار ينطلق من المصدر في مخطط ثنائية الأبعاد
قد نحتاج أحيانًا إلى العثور على أقصر مسار من مصدر معيّن إلى جميع العقد الأخرى، أو إلى عقدة محدّدة في مخطط ثنائية الأبعاد.
على سبيل المثال: نريد أن نعرف عدد التحركات المطلوبة للفارس للوصول إلى مربع معين في رقعة الشطرنج، وهذه حالة خاصة من مشكلة أكبر، حيث تكون لدينا رقعة بعض مربعاتها محظورة (الفارس لا يمكنه الانتقال لبعض المربعات على الرقعة)، وعلينا العثور على أقصر مسار من مربع إلى آخر لا يمر عبر المربعات المحظورة.
في مثل هذه الحالات، يمكننا تحويل المربعات أو الخلايا إلى عقد، ونحل هذه المشكلة بسهولة باستخدام خوارزمية البحث بالعرض أولًا BFS. ستكون المصفوفات visited و parent و level جميعها مصفوفات ثنائية الأبعاد.
نأخذ جميع التحركات الممكنة لكل عقدة، ونحسب المسافة إلى العقد الأخرى عبر تحليل مسارات التحرك، ثم نضيف مصفوفة أخرى نسميها direction، والتي ستخزّن جميع التركيبات الممكنة للاتجاهات التي يمكننا الذهاب إليها. مثلا، هذه مصفوفة الاتجاهات الخاصة بالتحركات الأفقية والعمودية:
+----+-----+-----+-----+-----+ | dx | 1 | -1 | 0 | 0 | +----+-----+-----+-----+-----+ | dy | 0 | 0 | 1 | -1 | +----+-----+-----+-----+-----+
تمثل dx الحركة على المحور الأفقي x بينما تمثل dy الحركة على المحور العمودي y، ولا شك أن هناك طرق أخرى لتمثيل اتجاهات الحركة لكن يُفضل استخدام مصفوفة الاتجاهات لأنها أسهل وأبسط. كذلك هناك الكثير من التركيبات الممكنة للحركة، إذ يمكن أن تكون التحركات قُطرية أو قد تكون أكثر تعقيدًا مثل تحركات الحصان على رقعة الشطرنج.
وينبغي أن نضع في حسباننا الأمور التالية:
- إذا كانت أيّ من الخلايا محظورة فسيكون علينا أن نتحقق في كل حركة محتملة مما إذا كانت الخلية الحالية محظورة أم لا.
- علينا أن نتحقق أيضًا ممّا إذا كنا قد تجاوزنا الحدودَ، أي حدودَ المصفوفة.
- سنُعطى عدد الصفوف والأعمدة.
انظر المثال التوضيحي التالي:
Procedure BFS2D(Graph, blocksign, row, column): for i from 1 to row for j from 1 to column visited[i][j] := false end for end for visited[source.x][source.y] := true level[source.x][source.y] := 0 Q = queue() Q.push(source) m := dx.size while Q is not empty top := Q.pop for i from 1 to m temp.x := top.x + dx[i] temp.y := top.y + dy[i] if temp is inside the row and column and top doesn't equal to blocksign visited[temp.x][temp.y] := true level[temp.x][temp.y] := level[top.x][top.y] + 1 Q.push(temp) end if end for end while Return level
ناقشنا سابقًا أن خوارزمية البحث بالعرض أولا BFS لا تصلح إلا للمخططات غير الموزونة unweighted graphs، أما بالنسبة للمخططات الموزونة فسنحتاج إلى خوارزمية ديكسترا. وبالنسبة لدورات الأضلاع السلبية negative edge cycles فسنحتاج إلى خوارزمية بِِلمان - فورد. هناك مسألة أخرى ينبغي الانتباه إليها، وهي أنّ هذه الخوارزمية مخصّصة لإيجاد أقصر مسار من مصدر واحد، فإذا أردت العثور على المسافة من كل عقدة إلى جميع العقد الأخرى ستحتاج إلى استخدام خوارزمية بِلمان - فورد كذلك.
البحث عن المكونات المتصلة لمخطط غير موجهة باستخدام خوارزمية BFS
يمكن استخدام خوارزمية BFS للعثور على المكونات المتصلة connected components في مخطط غير موجه، ويمكن استخدامها أيضًا للتحقق مما إذا كان المخطط متصلًا أم لا، وسنفترض فيما يلي أنّنا نتعامل مع مخططات غير موجهة.
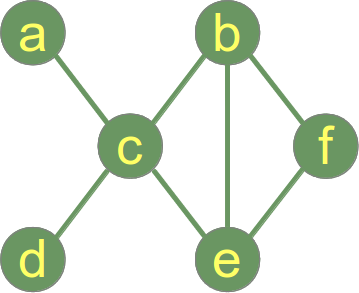
تعريف: يكون المخطط متصلًا connected إذا كان هناك مسار بين كل زوج من الحروف في المخطط. هذا مثال على مخطط متصل:
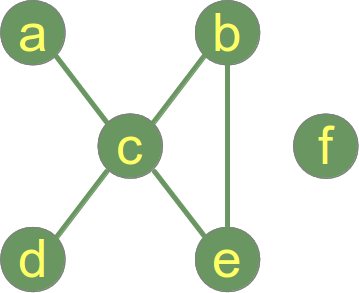
المخطط التالي غير متصل، ولكن يحتوي على مكوّنتين متصلتين:
- المكونة المتصل الأولى: {a، b، c، d، e} .
- المكون المتصلة الثانية: {f}
خوارزمية BFS هي خوارزمية لاجتياز المخططات، لذا إن بدأت الخوارزمية من عقدة مصدرية ما وانتقلت من عقدة إلى أخرى، ولم تترك عقدة إلا زارتها قبل انتهائها، فيكون المخطط في هذه الحالة متصلًا، أما إن بقيت بعض بعض العقد غير مُزارة، فسيكون المخطط غير متصل. انظر المثال التوضيحي التالي للخوارزمية:
boolean isConnected(Graph g) { BFS(v) // هي عقدة مصدرية v if(allVisited(g)) { return true; } else return false; }
وهذا تطبيق بلغة C للتحقق مما إذا كان مخططًا متصلًأ غير موجّه أم لا:
#include<stdio.h> #include<stdlib.h> #define MAXVERTICES 100 void enqueue(int); int deque(); int isConnected(char **graph,int noOfVertices); void BFS(char **graph,int vertex,int noOfVertices); int count = 0; struct node { int v; struct node *next; }; typedef struct node Node; typedef struct node *Nodeptr; Nodeptr Qfront = NULL; Nodeptr Qrear = NULL; char *visited;// مصفوفة لتتبع العقد المُزارة int main() { int n,e;// يمثل n عدد الحروف، ويمثل e عدد الأضلاع int i,j; char **graph;//adjacency matrix printf("Enter number of vertices:"); scanf("%d",&n); if(n < 0 || n > MAXVERTICES) { fprintf(stderr, "Please enter a valid positive integer from 1 to %d",MAXVERTICES); return -1; } graph = malloc(n * sizeof(char *)); visited = malloc(n*sizeof(char)); for(i = 0;i < n;++i) { graph[i] = malloc(n*sizeof(int)); visited[i] = 'N';// في البداية، تكون جميع العقد غير مزارة for(j = 0;j < n;++j) graph[i][j] = 0; } printf("enter number of edges and then enter them in pairs:"); scanf("%d",&e); for(i = 0;i < e;++i) { int u,v; scanf("%d%d",&u,&v); graph[u-1][v-1] = 1; graph[v-1][u-1] = 1; } if(isConnected(graph,n)) printf("The graph is connected"); else printf("The graph is NOT connected\n"); } void enqueue(int vertex) { if(Qfront == NULL) { Qfront = malloc(sizeof(Node)); Qfront->v = vertex; Qfront->next = NULL; Qrear = Qfront; } else { Nodeptr newNode = malloc(sizeof(Node)); newNode->v = vertex; newNode->next = NULL; Qrear->next = newNode; Qrear = newNode; } } int deque() { if(Qfront == NULL) { printf("Q is empty , returning -1\n"); return -1; } else { int v = Qfront->v; Nodeptr temp= Qfront; if(Qfront == Qrear) { Qfront = Qfront->next; Qrear = NULL; } else Qfront = Qfront->next; free(temp); return v; } } int isConnected(char **graph,int noOfVertices) { int i; // نختار العقدة 0 لتكون عقدة مصدرية BFS(graph,0,noOfVertices); for(i = 0;i < noOfVertices;++i) if(visited[i] == 'N') return 0;//0 implies false; return 1;//1 implies true; } void BFS(char **graph,int v,int noOfVertices) { int i,vertex; visited[v] = 'Y'; enqueue(v); while((vertex = deque()) != -1) { for(i = 0;i < noOfVertices;++i) if(graph[vertex][i] == 1 && visited[i] == 'N') { enqueue(i); visited[i] = 'Y'; } } }
للعثور على جميع المكونات المتصلة لمخطط غير موجه، يكفي أن نضيف سطرين إلى شيفرة الدالة BFS. الفكرة هي أن نستدعي الدالة BFS إلى أن تُزار جميع الحروف.
هذا هو السطر الأول، المتغير count هو متغير عام مهيء على القيمة 0، وهذا السطر يوضع في بداية دالة BFS:
printf("\nConnected component %d\n",++count);
وهذا هو السطر الثاني، اجعله في بداية حلقة while في دالة BFS:
printf("%d ",vertex+1);
نعرّف الآن الدالة التالية:
void listConnectedComponents(char **graph,int noOfVertices) { int i; for(i = 0;i < noOfVertices;++i) { if(visited[i] == 'N') BFS(graph,i,noOfVertices); } }
خوارزمية البحث بالعمق أولا Depth First Search
خوارزمية البحث بالعمق أولًا DFS هي خوارزمية لتسلق مخطط أو البحث فيها، وتبدأ من الجذر وتستكشف العقد على طول كل فرع وتتعمق فيه إلى آخر حدّ قبل أن ترتد backtrack، وقد استُخدِمت نسخة أولية من هذه الخوارزمية من قبل عالم الرياضيات الفرنسي تشارلز بيير Trémaux في القرن التاسع عشر لإيجاد حلول للمتاهات.
البحث بالعمق أولًا هي طريقة تحاول العثور على جميع العقد التي يمكن الوصول إليها من العقدة المصدر، وتجتاز خوارزمية DFS عقد مُكوّنة متصلة connected component ما من مخطط خوارزمية البحث بالعرض أولًا، ثم تعرّف شجرة ممتدة spanning tree. كذلك تستكشف خوارزمية البحث بالعمق أولا كل الأضلاع بطريقة منهجية. إذ تبدأ من العقدة المصدرية، وبمجرد الوصول إلى عقدة من المخطط تبدأ خوارزمية DFS في الاستكشاف انطلاقًا منها (على عكس خوارزمية BFS، التي تضعها في طابور لأجل استكشافها لاحقًا).
انظر المثال التالي:
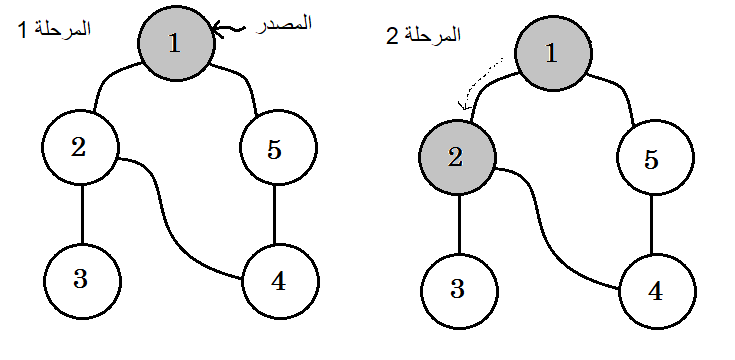
نجتاز المخطط باستخدام القواعد التالية:
- نبدأ من المصدر.
- لن نزور أيّ عقدة مرتين.
- نلوّن العقد التي لم نزرها بعد باللون الأبيض.
- نلوّن بالرمادي العقد التي زرناها ولكن لم نزر بعد جميع العقد المتفرّعة منها.
- نلوّن بالأسود العقد التي اجتزناها بالكامل هي والعقد المتفرعة منها.
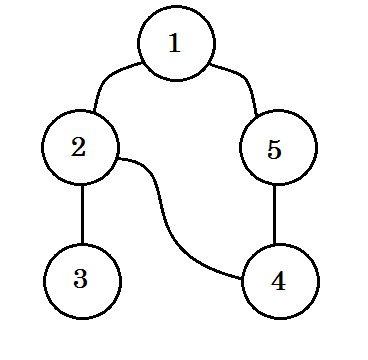
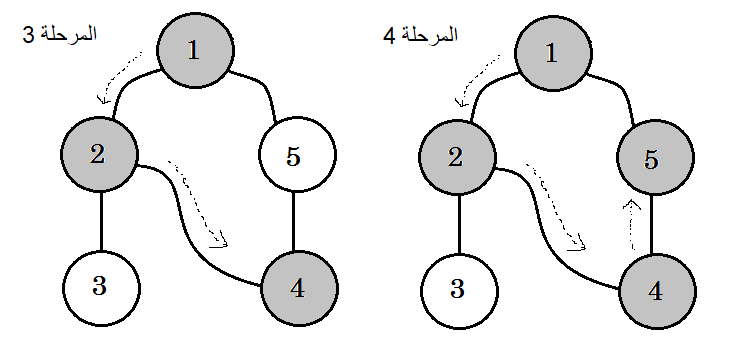
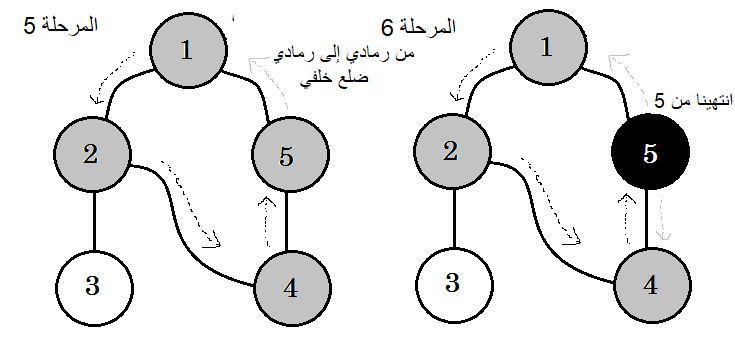
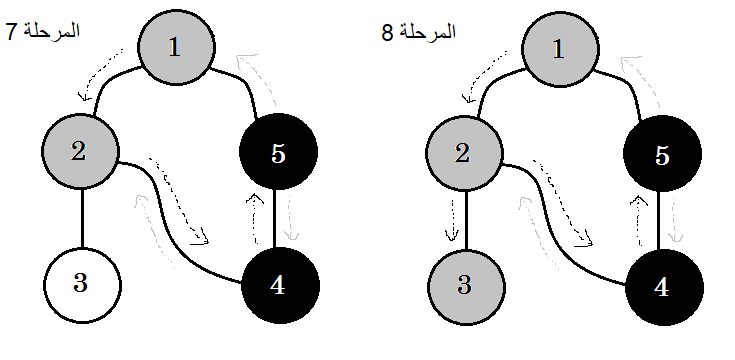
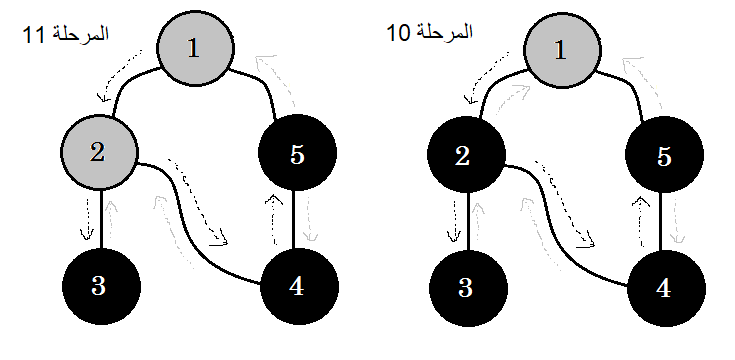
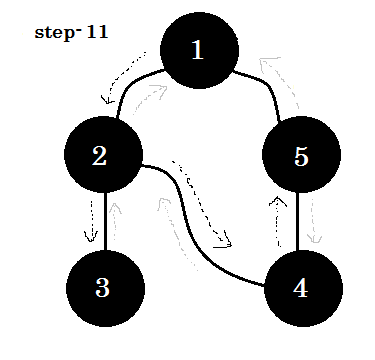
تبيّن الرسوم التالية هذه الخطوات:
الكلمة المفتاحية التي تهمنا والتي نراها فيما سبق هي الضلع الخلفي backedge، فالضلع 5-1 هو ضلع خلفي backedge، لأننا لم ننته بعد من العقدة 1، فالعودة إلى العقدة المصدرية 1 يعني وجود دورة في المخطط. إذا كنا نستطيع الانتقال من عقدة رمادية إلى أخرى في خوارزمية البحث بالعمق أولا، فذلك دليل على أنّ المخطط يحتوي على دورة، وهذه إحدى طرق رصد الدورات في المخططات.
يمكننا أن نجعل أيّ ضلع في الدورة كضلع خلفي اعتمادًا على العقدة المصدرية، وترتيب زيارة العقد. على سبيل المثال: لو انتقلنا إلى العقد 5 من العقدة 1 أولا، لوجدنا أنّ الضلع 2-1 أصبح ضلعًا خلفيًا.
تسمى الأضلاع التي تنتقل من عقدة رمادية إلى عقدة بيضاء أضلاع الشجرة أو أضلاعًا شجرية tree edge، وإذا أبقينا على أضلاع الشجرة وحذفنا الأضلاع الأخرى، فسوف نحصل على شجرة البحث بالعمق أولا DFS.
إذا استطعنا زيارة عقدة مزارة سابقًا في مخطط غير موجه فذلك يعني وجود ضلع خلفي، أمّا بالنسبة للمخططات الموجّهة فسيكون علينا أن نتحقق من الألوان، حيث يكون الضلع خلفيًا فقط إذا كان بمقدورنا الانتقال من عقدة رمادية إلى عقدة رمادية أخرى.
أيضًا، في خوارزمية البحث بالعمق أولا، نستطيع تخزين علامات زمنية timestamps لكل عقدة، تخزن هذه العلامات الزمنية معلومات عما حدث للعقد أثناء المعالجة، ونخزّنها في مصفوفتين، مصفوفة f لتخزين أوقات الانتهاء، ومصفوفة d لتخزين أوقات استكشاف العقد:
- عندما يتغيّر لون العقدة v من الأبيض إلى الرمادي نسجّل الوقت في الموضع d[v].
- عند يتغيّر لون عقدة v من الرمادي إلى الأسود، نسجّل الوقت في f [v].
سيبدو المثال التوضيحي لتخزين العلامات الزمنية كما يلي:
Procedure DFS(G): for each node u in V[G] color[u] := white parent[u] := NULL end for time := 0 for each node u in V[G] if color[u] == white DFS-Visit(u) end if end for Procedure DFS-Visit(u): color[u] := gray time := time + 1 d[u] := time for each node v adjacent to u if color[v] == white parent[v] := u DFS-Visit(v) end if end for color[u] := black time := time + 1 f[u] := time
التعقيد: تُزار كل عقدة وكل ضلع مرة واحدة، لذا فإن تعقيد خوارزمية DFS هو O (V + E)، حيث يمثّل V عدد العقد في المخطط، ويمثل E عدد الأضلاع.
التطبيقات على خوارزمية البحث بالعمق أولًا كثيرة، منها على سبيل المثال لا الحصر:
- العثور على أقصر مسار بين كل زوج من العقد في مخطط غير موجه.
- رصد الدورات في المخططات.
- العثور على المسارات.
- الترتيب التخطيطي (الطوبولوجي).
- التحقق ممّا إذا كان المخطط ثنائي التجزئة.
- العثور على المكونات شديدة الاتصال Strongly Connected Component.
- حل الألغاز التي لها حل واحد.
خوارزمية البائع المتجول
إن إنشاء مسار يمر عبر كل رأس من رؤوس المخطط مرة واحدة يكافئ ترتيبًا يرتّب حروف ذلك المخطط، ويمكننا استغلال هذه الخاصية لحساب التكلفة الدنيا لعبور كل رأس مرة واحدة بالضبط عبر تجريب كل التبديلات لمجموعة الأعداد من 1 إلى N، وعددها N!. انظر الشيفرة العامة لهذا:
minimum = INF for all permutations P // كل التبديلات current = 0 for i from 0 to N-2 // أضف تكلفة الانتقال من عقدة إلى إلى أخرى current = current + cost[P[i]][P[i+1]] // أضف تكلفة الانتقال من العقدة الأخيرة إلى إلى العقدة الأولى current = current + cost[P[N-1]][P[0]] if current < minimum // إن كان ذلك ضروريا minimum حدِّث minimum = current output minimum
التعقيد الزمني: هناك N! تبديلة ينبغي معالجتها، وحساب تكلفة كل مسار تستغرق O(N)، من ثم فإنّ هذه الخوارزمية تستغرق مدة O (N * N!).
استخدام البرمجة الديناميكية
انظر المسار:
(1,2,3,4,6,0,5,7)
والمسار
(1,2,3,5,0,6,7,4)
تبقى تكلفة الانتقال من العقدة 1 إلى العقدة 2 ثمّ إلى العقدة 3 كما هي، لذا ليس علينا إعادة حسابها، إذ يمكن أن نحفظ هذه النتيجة لاستخدامها لاحقًا.
لنفترض أنّ dp[bitmask][vertex] تمثل الحد الأدنى لتكلفة المسارات التي تعبر جميع الحروف التي قيمة البتّات المقابلة لها فيها bitmask تساوي 1، والتي تنتهي عند الحرف vertex. على سبيل المثال:
dp[12][2] 12 = 1 1 0 0 ^ ^ vertices: 3 2 1 0
نظرًا لأنّ 1100 هي التمثيل الثنائي لـ 12، فإنّ dp[12][2] تمثل الانتقال عبر الحرفين 2 و 3 في المخطط عبر مسار ينتهي عند الحرف 2.
هذا تطبيق على الخوارزمية بلغة C++:
int cost[N][N]; // إن كان ذلك ضروريا N تعديل قيمة int memo[1 << N][N]; // -1 تهيئة كل العناصر بالقيمة int TSP(int bitmask, int pos){ int cost = INF; if (bitmask == ((1 << N) - 1)){ // استكشاف كل العقد return cost[pos][0]; // تكلفة الرجوع } if (memo[bitmask][pos] != -1){ // إن كنا قد حسبنا هذه القيمة سابقا return memo[bitmask][pos]; // فسنعيد القيمة السابقة، فلا داعي لإعادة حسابها } for (int i = 0; i < N; ++i){ if ((bitmask & (1 << i)) == 0){ //إن لم تُكن العقدة مُزارة بعد cost = min(cost,TSP(bitmask | (1 << i) , i) + cost[pos][i]); // زيارة العقدة } } memo[bitmask][pos] = cost; // حفظ النتيجة return cost; } //Call TSP(1,0)
قد يكون هذا السطر مبهمًا، لذا سنفصِّله من أجل التوضيح:
cost = min(cost,TSP(bitmask | (1 << i) , i) + cost[pos][i]);
هنا، تعيّن العبارة bitmask | (1 << i) البتة رقم i في bitmask وتعطيها القيمة 1 دلالة على أنّ الحرف رقم i قد تمت زيارته.
تمثّل i الموضوعة بعد الفاصلة قيمة الموضع pos الجديد في هذا الاستدعاء، والذي يمثل الحرف الأخير الجديد. وتضيف العبارةcost[pos][i] تكلفة الانتقال من الحرف الموجود في الموضع pos إلى الحرف i.
يُحدّث هذا السطر قيمة cost، ويعطيها أدنى قيمة ممكنة للمرور عبر كل الحروف الأخرى التي لم تُزر بعد.
التعقيد الزمني: هناك 2^N قيمة ممكنة لـ bitmask و N قيمة ممكنة لـ pos في الدالة TSP(bitmask,pos). ويستغرق تنفيذ كل دالة O(N) (الحلقة for). وبالتالي يستغرق هذا التطبيق إجمالا مدة O(N^2 * 2^N) لإيجاد الحل النهائي.
خوارزمية كثيرة الحدود ومقيدة زمنيًا للعثور على أصغر غطاء رأسي
تعريف: ليكن G مخطط، و C مجموعة من حروفها، فنقول أنّ C غطاء رأسي للمخطط G إن كانت تحتوي طرفًا واحدًا على الأقل من كل ضلع من أضلاع المخطط. وفي هذه الفقرة نستعرض خوارزمية كثيرة الحدود للحصول على أصغر غطاء رأسي vertex cover لمخطط متصل غير موجّه.
التعقيد الزمني لهذه الخوارزمية يساوي O (n2).
هذا مثال توضيحي لخوارزمية أصغر غطاء رأسي، إذ نُدخل إليها مخططًا متصلًا G لتعيد لنا مجموعة C تمثّل أصغر غطاء رأسي لهذا المخطط.
Set C <- new Set<Vertex>() Set X <- new Set<Vertex>() X <- G.getAllVerticiesArrangedDescendinglyByDegree() for v in X do List<Vertex> adjacentVertices1 <- G.getAdjacent(v) if !C contains any of adjacentVertices1 then C.add(v) for vertex in C do List<vertex> adjacentVertices2 <- G.adjacentVertecies(vertex) if C contains any of adjacentVertices2 then C.remove(vertex) return C
يمكنك استخدام ترتيب الدلو لترتيب الحروف بحسب درجاتها، وبما أن القيمة القصوى للدرجات تساوي (n-1)، حيث يمثّل n عدد الحروف، فستستغرق عمليات الترتيب O(n).
ترجمة -بتصرّف- للفصول 41 و 42 و 44 و 53 من كتاب Algorithms Notes for Professionals.










أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.