تستعرض هذه المقالة مفهوم التعقيد Complexity، وهو أحد المفاهيم الأساسية في علم الخوارزميات، مع ذكر بعض أهم أصناف التعقيد وبعض الترميزات المستخدمة في ذلك.
ترميز Big-Omega
تُستخدم ترميز Ω -notation لتمثيل المقارِب الأدنى asymptotic lower bound.
التعريف الرسمي
لتكن fn) و g(n) دالتين مُعرّفتين على مجموعة الأعداد الحقيقية الموجبة، فنقول أنّ f(n) = Ω(g(n)) في حال وُجِدت ثابتان موجبان c و n0 يحققان الآتي لكل n أكبر من أو تساوي n0:
0 ≤ c g(n) ≤ f(n)
اقتباسملاحظة: المعادلة
f(n) = Ω(g(n))تعني أنّf(n)لا يمكن أن تنمو تقاربيًا asymptotically بشكل أبطأ منg(n)، كذلك يمكن كتابةΩ( g( n ))عندما لا يؤكّد تحليل الخوارزمية أنّΘ(g(n))أو /O(g(n)).
نظرية
بالنسبة لدالتين f(n) و g(n)، نقول أنّ f(n) = Ө(g(n)) فقط إذا كان الآتي محققًا:
-
f(n) = O(g(n)). -
f(n) = Ω(g(n)).
يمكن تمثيل ترميز Ω بيانيًا على النحو التالي:
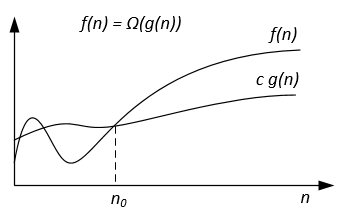
على سبيل المثال، إذا كانت
f(n) = 3n^2 + 5n - 4
فستكون f(n) = Ω(n^2)، كما ستكون f(n) = Ω(n) أو حتى f(n) = Ω(1) صحيحة.
لدينا مثال آخر يحل خوارزمية التطابق التام matching algorithm، حيث إذا كان عدد الرؤوس vertices فرديًا، فسنحصل على الخرج "No Matching Matching"، وإلا فينبغي تجربة جميع التطابقات الممكنة.
وكنا نودّ القول أنّ الخوارزمية تتطلب وقتًا أسيًا exponential time، لكن الواقع أنه لا يمكنك إثبات وجود حدّ أدنى Ω(n^2) باستخدام التعريف المعتاد لـ Ω نظرًا لأنّ الخوارزمية تُجرى في وقت خطي linear time لقيم n الفردية.
وبدلًا من هذا فيجب علينا تعريف f(n)=Ω(g(n)) على نحو أنه بالنسبة لثابت c قيمته أكبر من الصفر، فهناك عدد لا نهائي من قيم n التي تحقّق الآتي:
f(n)≥ c g(n)
يوفّق هذا التعريف بين الحدّين الأعلى والأدنى إذ يحقّق التكافؤ الآتي:
f(n)=Ω(g(n))
فقط إن كان
f(n) != o(g(n))
ترميز Big-Theta
على خلاف ترميز Big-O الذي يمثل الحد الأعلى upper bound فقط من وقت تشغيل الخوارزميات، فإنّ ترميز Big-Theta هو رابط محصور Tight bound يشمل الحدّ العلوي والسفلي معًا، وهو أكثر دقة لكنه صعب الحساب.
وترميز Big-Theta متماثلة، أي تحقق المعادلة:
f(x) = Ө(g(x)) <=> g(x) = Ө(f(x))
ولتفهم ذلك بسهولة، اعلم أن المعادلة الآتية
f(x) = Ө(g(x)) <=> g(x) = Ө(f(x))f(x) = Ө(g(x))
تعني أنّ الرسمين البيانيين للدالتين f و g ينمُوان بنفس المعدّل، أو أنّ الرسمين البيانيين "يتصرّفان" بشكل متماثل عند قيم x الكبيرة.
والتعبير الرياضي الكامل لترميز Big-Theta هو كما يلي:
Ө(f(x)) = {g: N0 -> R and c1, c2, n0 > 0}
حيث تكون
c1 < abs(g(n) / f(n))
لكل n أكبر من n0، وتمثل abs القيمة المطلقة.
ﻣﺜــــﺎل
إذا كانت الخوارزمية تأخذ العدد الآتي عمليةً للانتهاء مقابل مُدخل n، فنقول أنّ تعقيدها يساوي O(n^2) ، كما يساوي أيضًا O(n^3) وO(n^100).
42n^2 + 25n + 4
أمّا في حال ترميز Big-Theta، فنقول أنّ التعقيد يساوي Ө(n^2)، لكن لا يساوي Ө(n^3) أو Ө(n^4)، إلخ… . كذلك، فإن كانت الخوارزمية من نوع Ө(f(n))، فستكون أيضًا من النوع O(f(n))، ولكن ليس العكس.
التعريف الرياضي
تُعرّف Ө(g(x)) على أنها مجموعة من الدوال، أما تعريفها الرياضي الرسمي Formal mathematical definition فهو:
Ө(g(x)) = f(x)}
وإذا كانت هناك ثوابت موجبة N وc1 و c2، بحيث يكون
0 <= c1*g(x) <= f(x) <= c2g*(x)
لكل x أكبر من N}.
وهذا يعني أنّ Ө(g(x)) هي مجموعةٌ تحتوي كلّ دالة f مُحاصَرة من قبل الدالة g، بمعنى أنّه توجد 3 ثوابت موجبة هي c1 و c2 وN، بحيث يكون لدينا: 0 <= c1*g(x) <= f(x) <= c2*g(x) لكل عدد x أكبر من N.
وبما أن Ө(g(x)) مجموعةً فيمكننا كتابة الآتي للإشارة إلى أنّ f(x) تنتمي إلى Ө(g(x)).
f(x) ∈ Ө(g(x))
غير أن الشائع هو كتابة الآتي للتعبير عن نفس الترميز:
f(x) = Ө(g(x))
ويمكن تفسير Ө(g(x)) عندما تظهر في ترميز ما على أنّها كناية عن دالة مجهولة لا تهمّنا تسميتها، فمثلًا، المعادلة الآتية:
T(n) = T(n/2) + Ө(n)
تكافئ
T(n) = T(n/2) + f(n)
حيث تمثّل f(n) دالةً ما من المجموعة Ө(n)ا
وإن كانت f و g دالتين مُعرَّفتين على نفس النطاق من مجموعة الأعداد الحقيقية real numbers، فإننا نكتب الآتي:
f(x) = Ө(g(x))
عندما تؤول x إلى ما لا نهاية x->infinity، وذلك فقط في حالة وجود ثابتْين موجبيْن K و L وعدد حقيقي x0 يحققون
K|g(x)| <= f(x) <= L|g(x)|
لكل x أكبر من أو تساوي x0.
يكون التعريف مكافئًا للعبارة التالية:
f(x) = O(g(x))
والعبارة:
f(x) = Ω(g(x))
استخدام مفهوم النهايات limits
إذا كان لدينا
limit(x->infinity) f(x)/g(x) = c ∈ ( 0,∞)
أي أنّ النهاية موجودة وموجبة، أي:
f(x) = Ө(g(x))
وفيما يلي بعض أصناف التعقيد الشائعة:
| الاسم | الترميز | n = 10 | n = 100 |
|---|---|---|---|
| Constant - ثابت | Ө(1) | 1 | 1 |
| Logarithmic - لوغارتمي | Ө(log(n)) | 3 | 7 |
| Linear - خطي | Ө(n) | 10 | 100 |
| Linearithmic - لوغارتمي-خطي | Ө(n*log(n)) | 30 | 700 |
| Quadratic - تربيعي | Ө(n^2) | 100 | 10000 |
| Exponential - أسّي | Ө(2^n) | 1024 | 1.267650e+ 30 |
| Factorial - مُعاملي | Ө(n!) | 3 628 800 | 9.332622e+157 |
موازنة الصيغ المقاربة asymptotic notations
لتكن f(n) و g(n) دالتين مُعرّفتين على مجموعة الأعداد الحقيقية الموجبة، ولتكن c, c1, c2, n0 ثوابت حقيقية موجبة.
يوضّح الجدول التالي الفروق بين مختلف الصيغ:
| الترميز | f(n) = O(g(n)) | f(n) = Ω(g(n)) | f(n) = Θ(g(n)) | f(n) = o(g(n)) | f(n) = ω(g(n)) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| التعريف الرسمي | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) ≤ c g(n) | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) ≤ f(n) | ∃ c1, c2 > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) < c g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) < f(n) | ||||||||
| التشابه مع الموازنة بين عددين a وb | a ≤ b | a ≥ b | a = b | a < b | a > b | ||||||||
| أمثلة | 7n + 10 = O(n^2 + n - 9) | n^3 - 34 = Ω(10n^2 - 7n + 1) | 1/2 n^2 - 7n = Θ(n^2) | 5n^2 = o(n^3) | 7n^2 = ω(n) | ||||||||
|
|
|
|
يمكن تمثيل الصيغ المُقارِبة بواسطة مخطّط فِن كما يلي:
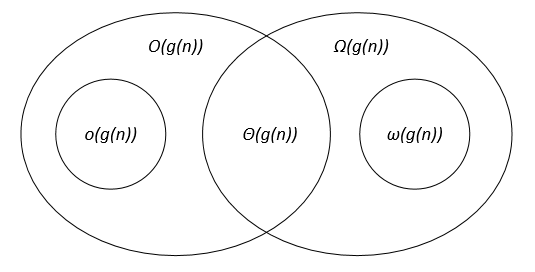
ترجمة -بتصرّف- للفصل الثاني من كتاب Algorithms Notes for Professionals










أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.