سنوضح في هذا المقال الأدوات الرياضية المُستخدَمة في الرسوميات الحاسوبية ثلاثية الأبعاد Three Dimensional Computer Graphics -أو 3D Graphics اختصارًا، إذ يبني برنامج الرسوميات ثلاثية الأبعاد مشهدًا مكونًا من كائنات ثلاثية الأبعاد في فضاء ثلاثي الأبعاد، ثم تُنتَج صور ثنائية الأبعاد من المشهد ثلاثي الأبعاد، ويُمثَّل المشهد بوصفه هيكل بيانات في ذاكرة الحاسوب، وتُعَد الصورة ثنائية الأبعاد عادةً هي الصورة الموجودة على واجهة شاشة الحاسوب.
تتكون الكائنات ثلاثية الأبعاد من نقاط وخطوط ومضلعات، إذ لا بد أنك تعرف ماهية هذه المفاهيم، ولكننا سنوضح في هذا المقال هذه المفاهيم ونقدم بعض المفردات الخاصة بالرسوميات الحاسوبية حتى نبدأ من أرضية مشتركة، إذ سنتعرّف على المواضيع التالية:
- النقاط.
- الخطوط.
- المثلثات.
- تمثيل النقاط والخطوط.
- إطارات الإحداثيات.
- تحديد الإحداثيات.
- تأثير تغيير الإطارات على الإحداثيات.
- الأشعة.
- تمثيل الأشعة.
هناك شيئان أساسيان في الهندسة هما النقاط والخطوط، إذًا لنتعرف على هذين المفهومين، ولكن لنبدأ بالإجابة على سؤال "ما هي النقطة؟".
النقطة
ما هي النقطة؟ النقطة هي موقع في الفضاء.
النقطة الهندسية هي موقع في الفضاء بدون أيّ خصائص أخرى، إذ لا تملك طولًا أو عرضًا أو سماكة، وتعَد موقعًا مجردًا. لن يساعدك هذا التعريف لمفهوم النقطة إن لم يكن لديك فهمٌ مسبق له، إذ تشير عبارة "موقع في الفضاء" إلى مفهوم كلمة "نقطة" نفسه، ولا يمكن للتعريف أن ينقل لك مفهومًا لا تملكه مسبقًا.
لا يوجد تعريف لكلمة نقطة في الهندسة، فالنقطة هي إحدى المفاهيم الأولية غير المُعرَّفة التي تُستخدَم لتعريف الكائنات الأخرى، إذ تعطي الكتب أمثلةً عنها وتأمل أن تبني بنفسك مفهومًا منها بطريقةٍ ما بدلًا من إعطائك تعريفًا لها.
تُظهر الصورة التالية قبتين على أحد المباني، وتُعَد هذه الصورة ثنائية الأبعاد، لكن فكّر في المبنى الفعلي ثلاثيّ الأبعاد، وركّز على القضيب المعدني (النهائي) الموجود أعلى القبة الأقرب.
إذًا، تحدّد النهايةُ الحادة للقضيب المعدني موقعًا دقيقًا بحسب مقياس المبنى، إذ يمكننا تصور هذا الموقع بوصفه نقطة.
ما هي النقاط فيزيائيا؟
لنفترض أن هذا القضيب المعدني أمامك على مكتبك، فهل تُعَد نهايته نقطة؟ غالبًا لا، إذ تكون النهاية غير حادة جدًا بحسب هذا المقياس، بحيث لا يمكن عدّها نقطة.
تعبّر النقطة عن المثالية، إذ تكون نهاية القضيب المعدني بحسب مقياس المبنى صغيرةً بما يكفي لعَدّها موقعًا محددًا، وبالتالي يمكن عدّها نقطة، ولكن تكون نهايته غير حادة جدًا بحسب مقياس مكتبك بحيث لا يمكنها تحديد موقع واحد فعلًا. يجب أن يتناقص حجم هذا القضيب المعدني إلى حجم الدبوس بحسب مقياس المكتب، وبالتالي يمكنك أن تحدّد نهايته نقطةً ما.
لكن إذا وضعت الدبوس تحت المجهر، فستكون نهايته غير حادة جدًا بالنسبة لهذا المقياس مرة أخرى، وبالتالي يجب أن تتقلص أكثر إلى حجم البكتيريا مثلًا قبل أن تتمكن النهاية من تحديد نقطة ما، لكن أصبحت نهاية القضيب المعدني مرةً أخرى سميكةً جدًا بحسب مقياس البكتيريا بحيث لا يمكنها تحديد الموقع بدقة.
إذًا تعبّر النقاط في الفضاء ثلاثي الأبعاد عن المثالية، إذ تكون النهاية الحادة للقضيب المعدني دقيقةً بما يكفي لتكون نقطة بالنسبة لنموذج المبنى الحاسوبي، ولا يلزم تحديد الحواف والمستويات والأشكال الأخرى التي يتكون منها المبنى بدقة أكبر.
النقاط في الفضاء
ما هو موقع نهاية القضيب المعدني الأبعد في الفضاء؟ انظر إلى الصورة مرةً أخرى وتخيل العلاقة بين نقطتي نهايتي القضيبين المعدنيين، إذ لا توجد إجابة فعلية ضرورية حاليًا.
تكون نقاط النهاية للقضيبين المعدنيين في مواقع محدّدة من العالم الحقيقي real world، وسنحدّد هذه المواقع باستخدام إطار إحداثي لاحقًا، ولكن لنفكر الآن فقط في النقاط الموجودة في الفضاء. تضع في برامج الرسوميات ثلاثية الأبعاد نقاطًا وخطوطًا وأشياءً أخرى في الفضاء، ثم تسقطها على صورة ثنائية الأبعاد، ويحاكي ذلك ما حدث عند إنتاج الصورة باستخدام الكاميرا، إذ تكون نهايات القضيبين المعدنيين فيزيائيًا نقاطًا في الفضاء ثلاثي الأبعاد. تسقط العدسة كامل المشهد على مستشعر الصور ثنائية الأبعاد، وتحدد نهايات القضبان المعدنية في الصورة ثنائية الأبعاد نقطتين ثنائيتي الأبعاد.
الخطوط
ما المسافة بين النقطتين عند طرفي القضيبين المعدنيين؟ يمكن أن نخمن أن المسافة حوالي 30 مترًا.
يكون الحكم على العمق صعبًا في الصورة ثنائية الأبعاد في أغلب الأحيان، إذ تُفقَد معلومات العمق عند إنتاج صورة ثنائية الأبعاد من مشهد ثلاثي الأبعاد (إما مشهد حقيقي أو مشهد في الحاسوب). فكر الآن في القطعة المستقيمة Line Segment الواقعة بين النقطتين، والتي هي المسار المستقيم بين نقطتين بدون سماكة، ولا توجد سوى قطعة مستقيمة واحدة بين النقطتين.
إن لم يكن لديك مفهوم مسبق عن "الخط"، فلن يكون التعريف السابق كافيًا لتعلمه، إذ تشير عبارة "المسار المستقيم" إلى مفهوم الخط الذي عرّفناه. تتعامل غالبًا مع القطع المستقيمة في الرسوميات ثلاثية الأبعاد، بينما تستمر الخطوط بلا نهاية في الهندسة، إذ تكون القطعة المستقيمة جزءًا من الخط بين نقطتين.
لا يُعرَّف الخط العالمي في كتب الهندسة عادةً، وهو -مثل النقطة- مفهوم غير مُعرَّف يستخدم لتعريف كائنات أخرى، إذ تقدّم الكتب صورًا وأمثلة عن الخطوط، وتأمل أن تفهم بطريقة أو بأخرى ما هو الخط من خلال النظر إليها. يستخدم بعض الأشخاص مصطلح "خط" بينما يجب عليهم استخدام مصطلح "قطعة مستقيمة" الذي سنستخدمه في هذا المقال، نظرًا لأن القطع المستقيمة شائعة جدًا.
القطع المستقيمة
هل يمكنك تمديد stretch طول السلك بين النقطتين؟ نعم، من الناحية المفاهيمية على الأقل.
يوجد سلك رفيع ممتد بين القضيبين المعدنيين بحسب مقياس المبنى، والذي يعبر عن تقريبٍ لقطعة مستقيمة، وكما تعلم يتعلق هذا الأمر بالمقياس، إذ يُرجَّح أن يكون السلك أسمك من الخط المرسوم بقلم رصاص، فالسلك الموجود على مكتبك سميك جدًا بحيث لا يمكن عدّه قطعة مستقيمة. بينما يكون الخط المرسوم بقلم الرصاص الرفيع والمستقيم رفيعًا بدرجة كافية لعدّه خطًا هندسيًا، وإذا كان سميكًا جدًا، فيمكن أن يكون طول خيط العنكبوت الممتد بين نقطتين مناسبًا.
لكن يمكن عَدّ الأسلاك المدروسة على المستوى المعماري بمثابة قطع مستقيمة، ويمكنك بناء نموذج هندسي للمبنى باستخدام القطع المستقيمة لتمثيل الحواف.
المثلثات
جرّب رسم مثلث يربط بين القضيبين المعدنيين والزاوية العلوية اليسرى من السور الأبيض كما في الصورة التالية:
يمكن إنشاء المثلث من خلال ربط ثلاث نقاط في فضاء ثلاثي الأبعاد بقطع مستقيمة، فإذا لم تقع النقاط الثلاث جميعها على الخط نفسه، فستحدّد ثلاث نقاط في الفضاء مثلثًا فريدًا. تُعَد المثلثات الموجودة في الفضاء مهمةً في الرسوميات ثلاثية الأبعاد، إذ تُنشَأ الكائنات ثلاثية الأبعاد التي تشكّل المشهد من المثلثات والمضلعات المسطحة الأخرى. المثلث الموجود في الصورة ثنائية الأبعاد هو إسقاط للمثلث ثلاثي الأبعاد في المشهد، ولكن يشوه الإسقاطُ المثلثَ ثلاثيّ الأبعاد، فالمثلث ثلاثي الأبعاد أكبر بكثير من المثلث ثنائي الأبعاد، وتكون الزوايا مختلفة.
لنفترض أن الكائن ثلاثي الأبعاد في المشهد مكونٌ من عدة مثلثات، ولنسقط كل مثلث على صورة ثنائية الأبعاد، والنتيجة هي النسخة المُسقَطة من الكائن ثلاثي الأبعاد. يتكون السور الشبكي الأبيض في المبنى من العديد من المثلثات، وتُظهِر نسخة السور الشبكي الموجودة في الصورة جميع هذه المثلثات التي تسقطها عدسة الكاميرا.
التمثيل باستخدام إطار إحداثيات
هل تحتاج إلى إطار إحداثي -أي نظام مع تسمية النقاط بالإحداثيات x و y و z- للحديث عن النقاط والخطوط والأشكال المستوية؟ في الحقيقة لا حاجة لذلك.
يمكنك التفكير في النقاط والخطوط والأشكال المستوية التي تشكّل المشهد ثلاثي الأبعاد دون استخدام نظام إحداثي، وهذا ما كنا نفعله في الحقيقة، ولكن يجب تمثيل هذه الكائنات بطريقة أو بأخرى والتعامل معها في رسوميات الحاسوب، ولذلك نحتاج إلى طريقة لتمثيلها.
اختر نقطةً مناسبة في المشهد ثلاثي الأبعاد وأطلِق عليها اسم نقطة الأصل Origin، وحدد ثلاثة خطوط تسمى X و Y و Z والتي تمر عبر نقطة الأصل، وتكون الخطوط الثلاثة عادةً متعامدة على بعضها بعضًا، ويسمى كل خط محورًا Axis. اختر اتجاهًا إيجابيًا لكل خط، فهناك عدة خيارات لذلك، ولكن لنستخدم الخيار الموضّح في الصورة السابقة. تمثل كل نقطة من المحور X مسافةً فريدةً (موجبة أو سالبة أو صفر) من نقطة الأصل، فمثلًا تقع زاوية المبنى الموجودة على المحور X على مسافة 2.4 متر (8 أقدام) تقريبًا من نقطة الأصل.
الإحداثيات
تقع نقطة الأصل على ارتفاع صفر، ولكن على أي ارتفاع تقع نقطة نهاية القضيب المعدني الأقرب تقريبًا؟ يمكن القول أن ارتفاعها حوالي 3.6 مترًا (10 أقدام).
أو يمكنك القول أن y=3.6 بالنسبة لنقطة نهاية القضيب المعدني، إذ يمكن إسناد تمثيل لأيّ نقطة في مشهدنا ثلاثيّ الأبعاد من خلال قياس المسافة على طول المحاور الثلاثة، إذ سنضع هذه المسافات الثلاث في مصفوفة عمودية على النحو التالي في هذا المقال (وفي العديد من كتب الرسوميات الحاسوبية):
قد تكون معتادًا على وضع الإحداثيات الثلاثة في صف ثلاثي مثل (x, y, z)، ولكن سيتبين أنه من الملائم أكثر وضعها في مصفوفة عمودية كما ذكرنا بالنسبة للرسوميات الحاسوبية، فمثلًا إحداثيات زاوية المبنى التي تقع على طول المحور X هي تقريبًا:
تحديد الإحداثيات
ما هي إحداثيات نقطة زاوية الشبكة البيضاء على طول الحافة العلوية (المسمَّاة P0)؟ يمكن القول أنها تقريبًا:
احسب عند تحديد الإحداثيات قياس المسافة على طول الخطوط الموازية لمحاور الإحداثيات، إذ ستشكّل الخطوط التي تستخدمها مستطيلًا أو أوجه صندوق.
تشكّل الخطوط السوداء المنقطة المستخدمة للنقطة Q0 مستطيلًا، ويعطي قياس أضلاع المستطيل الإحداثيات التالية:
من الصعب معرفة إحداثيات النقطة Q1، فالصورة ثنائية الأبعاد، ولكن المشهد الذي تظهره ثلاثي الأبعاد، وبالتالي فإن المحور Z مشوه، ولكن تشكل الخطوط المنقطة في المشهد ثلاثي الأبعاد صندوقًا، فقياس جميع الزوايا 90 درجة.
مزيد من النقاط
يمكن تقدير إحداثيات النقطة Q1 بالقيم التالية:
لنعُد الآن إلى مشهدنا الواقعي، إذ يبلغ طول الشبكة البيضاء تقريبًا حوالي 2.4 متر (8 أقدام) من كل جانب.
النقطة وتمثيلها
يمكن تخمين إحداثيات طرف القضيب المعدني الأقرب بالقيم التالية:
تُعَد المصفوفة العمودية كائنًا رياضيًا يمثل النقطة باستخدام إطار الإحداثيات الذي اخترناه، ولكن ليست هذه المصفوفة العمودية هي النقطة بحد ذاتها، فالمصفوفة العمودية والنقطة شيئان مختلفان، إذ يُستخدَم أحدهما لتمثيل الآخر مثل استخدام اسمك لتمثيلك.

نأمل أن يكون ذلك واضحًا، ولكنه سيكون غامضًا بالنسبة للطلاب الذين يحاولون تخطي مواضيع رياضيات الرسوميات الحاسوبية بسرعة، مما يؤدي إلى ندمهم في نهاية المطاف، إذ يمكن أن يمثل كتاب الرسوميات الحاسوبية النقطة نفسها بعدة طرق مختلفة، لذا من الضروري الفصل بين أفكار النقطة الهندسية والطرق المتعددة التي يمكن تمثيلها باستخدامها.
ملاحظة: يتحدث الأشخاص في أغلب الأحيان عرضيًا ويقولون أشياء مثل "النقطة (4, 12, -4)"، كما لو كان هذا الصف الثلاثي من الأرقام متطابقًا مع النقطة، ولكن يُستخدَم ذلك للراحة فقط، إذ ينبغي عليهم أن يقولوا: "النقطة المُمثَّلة في نظام الإحداثيات الذي اخترناه بالتمثيل (4, 12, -4)."
تأثير تغيير الإطارات على الإحداثيات
هل تقاس المسافات على طول محاور الإحداثيات بوحدة القدم أم بالأمتار؟ لا يهم، طالما أنك تستخدمها بصورة متناسقة.
لا تُوضَع إطارات الإحداثيات المستخدمة في كتب الرياضيات في مشهد من العالم الحقيقي عادةً، لذلك لا يُعبَّر عن المسافات بأيّ وحدة معينة، ولكن يتعين عليك تحديد الوحدات التي تستخدمها عندما تنشئ عالمًا ثلاثي الأبعاد في الحاسوب. تُظهر الصورة التالية عالمًا ثلاثيّ الأبعاد مع وضع إطارٍ إحداثي مختلف فيه، إذ تبقى النقاط في العالم نفسها كما كانت سابقًا، ولكن سيكون لديها تمثيلات مختلفة مع إطار إحداثي مختلف:
مثلنا النقطة المسمَّاة P1 بما يلي في الإطار السابق:
ستكون الآن المسافات على طول المحاور في الإطار الجديد (الأخضر) مختلفة، فالمصفوفة العمودية التي تمثل النقطة P1 في الإطار الجديد هي تقريبًا:
لم نمارس الرياضيات بصورة دقيقة هنا، بل نظرنا إلى الصورة وخمّنا المسافات فقط، لذا حاول أن تفعل الشيء نفسه، فالهدف ليس حساب أي شيء، بل التفكير في النقاط في الفضاء. للنقطة نفسها تمثيلات مختلفة في كل إطار، لذا يجب أن تعرف الإطار المُستخدَم عندما تمثل نقطةً بمصفوفة عمودية.
ضوء الشمس
يمكن تقدير إحداثيات النقطة P0 على الحافة العلوية للشبكة المبينة في الصورة أعلاه بالمصفوفة العمودية التالية:
ولكن هذه القيم مجرد تقدير فقط.
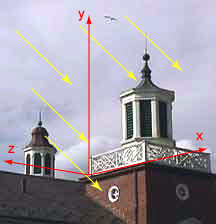
انظر إلى صورة المبنى مرةً أخرى، إذ تضيء الشمسُ المشهد، ولكنها ليست موجودة في الصورة، إذ يأتي ضوء الشمس في المشهد قطريًا من خارج المشهد إلى يساره.
الأشعة Vector
ارسم ذهنيًا بعض الخطوط في الصورة التي تظهر ضوء الشمس كما في الشكل التالي:
يتدفق الضوء من أعلى اليسار عندما تنظر إلى المبنى، إذ تمثل الصورة ضوء الشمس بأسهم. حاول التفكير في المشهد ثلاثي الأبعاد بالرغم من أن الصورة ثنائية الأبعاد، فالاتجاه الذي يتحرك فيه الضوء موضَّح بالسهم، ويمثل طول السهم مثلًا شدة الضوء. توجد عدة أسهم في الصورة، إلا أنّ أيّ سهمٍ يكفي لتمثيل الضوء وشدته.
يمكن تمثيل اتجاه الضوء وشدته بشعاع، والذي هو كائن هندسي له خاصيتان هما: الطول والاتجاه. للضوء الصادر من الشمس خاصيتان، هما: السطوع والاتجاه (مع تجاهل معلومات اللون)، ويتناسب طول الشعاع مع سطوع الضوء. يمكن تمثيل الرياح أيضًا بشعاع، فالرياح لها اتجاه وسرعة، إذ تنتقل ذرة من الغبار مع اتجاه الريح، ويتناسب طول الشعاع مع سرعة ذرة الغبار.
ليس للشعاع موضع، إذ تُظهِر الصورة السابقة عدة أسهم تمثل تدفق الضوء القادم من الشمس، ولكن يمكن رسم الأسهم في أيّ مكان طالما أن اتجاهها وطولها هو نفسه.
تمثيل الأشعة
هل تفترض أن برنامج الرسوميات الحاسوبية يحتاج إلى تمثيل شدة الضوء واتجاهه؟ نعم، في الحقيقة هناك حاجة لذلك.
تُستخدَم الأشعة لعدة أغراض في رسوميات الحاسوب ثلاثية الأبعاد، لذلك يجب أن تُمثَّل بطريقة يمكن للبرامج التعامل معها، ويحدث ذلك باستخدام الأرقام. لاحظ أن الصورة التالية تتضمن الآن إطار إحداثياتنا:
يُمثَّل الشعاع بمصفوفة عمودية كما هو الحال مع النقاط، ويمكن أن يكون من المربك إلى حدٍ ما أن تُمثَّل النقاط والأشعة باستخدام الشيء نفسه، ولكن ذلك سيثبت أنه هذه الطريقة مناسبة ليتعامل معها الحاسوب.
يمكن تمثيل الشعاع بمصفوفة عمودية باتباع الخطوات التالية:
- اختر إطارًا إحداثيًا.
- احسب طول X (موجب أو سالب) من ذيل الشعاع إلى رأسه. 3.احسب طول Y (موجب أو سالب) من ذيل الشعاع إلى رأسه.
- احسب طول Z (موجب أو سالب) من ذيل الشعاع إلى رأسه.
- ضع هذه الأرقام الثلاثة في عمود.
إحدى الطرق الملائمة لذلك هي وضع ذيل الشعاع عند نقطة الأصل، ثم قراءة قيم x و y و z عند رأسه.
الأشعة والإطارات
كم مترًا في الاتجاه X للمسافة بين رأس الأسهم عن ذيلها في الصورة؟ يمكن أن نخمنها بمقدار حوالي 0.9 متر (3 أقدام). كم مترًا في الاتجاه Y يبعد الرأس عن الذيل؟ يمكن أن نخمنها بمقدار 1.2- متر (-4 أقدام). كم مترًا في الاتجاه Z يبعد الرأس من الذيل؟ يمكن أن نخمنها بمقدار 0.9- متر (-3 أقدام).
إذًا، الشعاع الذي يعطي شدة واتجاه ضوء الشمس في الصورة هو:
تمثل المصفوفة العمودية السابقة الشعاع باستخدام إطار الإحداثيات الذي اخترناه، ولكنها ليست الشعاع نفسه. إذا اخترنا إطارًا إحداثيًا مختلفًا، فسيكون الشعاع في المشهد الحقيقي هو نفسه، ولكن سيتغير تمثيله باستخدام الإطار الجديد، وسنواصل في المقال التالي هذه المناقشة.
مراجعة سريعة:
- للنقطة خاصية واحدة فقط هي: الموقع.
- للشعاع خاصيتان، هما: الطول والاتجاه ولكن ليس له موقع.
ترجمة -وبتصرُّف- للفصل Points and Lines من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.








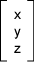
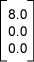
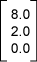
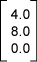
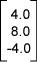

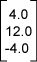


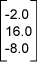




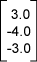











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.