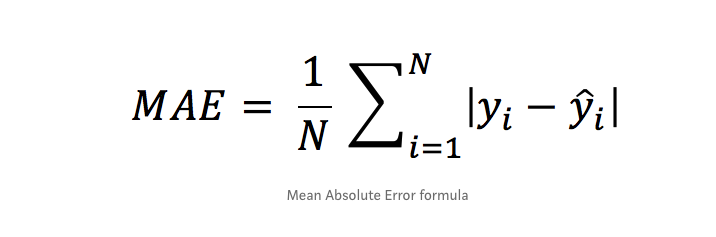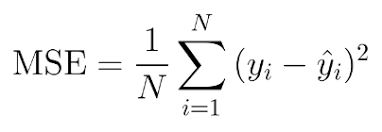لوحة المتصدرين
المحتوى الأكثر حصولًا على سمعة جيدة
المحتوى الأعلى تقييمًا في 06/09/21 في كل الموقع
-
لا يُنظر في عالم الحاسوب إلى شيء سوى إلى البيانات، حيث يمكنك أن تقرأ البيانات، وتُعدّلها، وتُنشِئ الجديد منها، بينما يُغفَل ذكر ما سواها، وهي متشابهة في جوهرها، إذ أنها تُخزَّن في سلاسل طويلة من البِتَّات Bits. ويُعبَّر عن البِتَّات بأي زوج من القيم، وتُكتَب عادةً بصورة الصفر والواحد، وتأخذ داخل الحاسوب أشكالًا أخرى، مثل: شحنة كهربائية عالية أو منخفضة، أو إشارة قوية أو ضعيفة، أو ربما نقطة لامعة أو باهتة على سطح قرص مدمج CD. لذلك توصَّف أيّ معلومة فريدة، في سلسلة من الأصفار والواحدات، ومن ثم تُمثَّل في بِتَّات. فمثلًا: نمثِّل العدد 13 بالبِتَّات، بالطريقة المعتمَدة في النظام العشري، إلا أنه يوجد لكل بِتّ، قيمتان فقط بدلًا من عشر قيم مختلفة، بحيث يزداد وزن كل بِتّ، ابتداءًا من اليمين إلى اليسار بمعامل العدد 2. ونحصل على البِتَّات المقابلة للعدد 13 مع بيان وزن كل بِتّ أسفل منها، كما يأتي: | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | وبذلك، مُثِّل العدد 13 بالعدد الثنائي 00001101، والذي نحصل عليه بجمع أوزان البِتّات الغير صفرية، أي بجمع: 8، و4، و1. القيم تخيّل أنّ ذاكرة الحاسوب بحر تتكوّن ذراته من بِتَّات صغيرة جدًا بدلًا من ذرّات الماء، حتى أنها أشبه بمحيط كبير يتكون من 30 مليار بِتّ في ذاكرته المتطايرة volatile فقط، وأكثر من هذا بكثير في ذاكرته الدائمة (الأقراص الصلبة وما شابهها). ولكي نستطيع العمل مع هذه الأعداد الهائلة من البِتّات دون التيه في متاهة منها، فإننا نقسّمها إلى قطع كبيرة تُمثِّل أجزاءً من معلومات، وتسمّى تلك القطع في لغة جافاسكربت، بالقيم Values، ورغم أن تلك القيم تتكوّن من بِتّات، إلا أنها تختلف في وظائفها اختلافًا كبيرًا، فكل قيمة لها نوع يُحدِّد وظيفتها ودورها، فقد تكون بعض تلك القيم أعدادًا، كما قد تكون نصًّا، أو دوالًا، وهكذا. وما عليك إلا استدعاء اسم القيمة لإنشائها، دون الحاجة إلى جمع مواد لها أو شرائها، بل بمجرّد استدعاء القيمة يجعلها بين يديك. وتُخزَّن تلك القيم في الذاكرة طبعًا، إذ يجب أن تكون في مكان ما، وقد تَنفد ذاكرة الحاسوب إذا استدعيت قيمًا كثيرة، وتحدث هذه المشكلة إذا احتجت جميع القيم التي لديك دفعةً واحدة. وتتبدّد القيم، بمجرّد انتهائك من استخدامها، تاركةً خلفها البِتّات التي شغلَتها، وذلك من أجل الأجيال المستقبلية من القيم. وسنشرح في هذا الفصل، العناصر الصغيرة جدًا في برامج جافاسكربت، وهي: أنواع القيم البسيطة، والعوامل Operators التي تعمل وفقًا لهذه القيم. الأعداد تُكتب القيم من النوع العددي في جافاسكربت على هيئة أعداد، أي على النحو التالي: 13 وإذا استخدمت القيمة أعلاه في برنامج ما، فسيُنشِئ النمط البِتّي لها في ذاكرة الحاسوب، وتستخدم جافاسكربت، لتخزين قيمة عددية واحدة، عددًا ثابتًا من البِتّات، ومقداره تحديدًا 64 بِتّ، مما يجعل عدد الأنماط التي يمكن إنشاؤها بأربع وستين بِتِّ، محدودًا نوعًا ما، وعدد الأعداد المختلفة التي يمكن تمثيلها، محدودًا أيضًا، إذ يمكنك تمثيل 10N عدد باستخدام رقم N من الأرقام العشرية، كما يمكنك تمثيل 264 عدد مختلِف باستخدام 64 رقم ثنائي أيضًا، ويُترجم هذا إلى نحو 18 كوينتليون (18 أمامها 18 صفرًا) عدد. ويُعَدّ حجم ذواكر الحاسوب قديمًا، موازنَةً بالأحجام والسعات الحالية، صغيرًا للغاية، حيث استخدم الناس، لتمثيل الأعداد، مجموعات من 8-بِتّ، أو 16-بِتّ، فكان من السهل جدًا تجاوز الحد المسموح به للأعداد التي يمكن تمثيلها فيها، لينتهي الأمر بعدد لا يمكن تمثيله ضمن العدد المعطى من البِتّات. أما الآن، فتملك الحواسيب التي تضعها في جيبك، ذواكرًا كبيرةً، مما يتيح لك استخدام مجموعات من 64-بت، ولا تقلق بشأن تجاوز ذلك الحد إلا إذا تعاملت مع أعداد كبيرة جدًا. ولكن رغم ما سبق، لا يمكن تمثيل كل الأعداد الأقل من 18 كوينتليون بعدد في جافاسكربت، حيث تُخزِّن البِتّات أيضًا أعدادًا سالبة، مما يعني أنه سيُخصَّص أحد البِتّات لتمثيل إشارة العدد، والمشكلة الأكبر هنا أنه يجب أيضًا تمثيل الأعداد الكسرية، وبالتالي سيُخصَّص بِتّ آخر لموضع الفاصلة العشرية، وذلك سيقلل عدد الأعداد التي يمكن تمثيلها بجافاسكربت، إلى 9 كوادريليون عدد (15 صفرًا هذه المرة)، وتُكتب الأعداد الكسرية fractional numbers على الصورة التالية: 9.81 وتستطيع استخدام الترميز العلمي لكتابة الأعداد الكبيرة جدًا أو الصغيرة جدًا، وذلك بإضافة e (للإشارة إلى وجود أس)، متبوعةً بأس العدد، حيث يُكتَب العدد 2.998 × 108 والمساوي لـ 299,800,000، بالشكل الآتي: 2.998e8 وتُضمَن الدقة في العمليات الحسابية المستَخدَمة مع الأعداد الصحيحة integers والأصغر من العدد المذكور آنفًا -9 كوادريليون-، على عكس العمليات الحسابية المستخدَمة مع الأعداد الكسرية، فكما أنه لا يمكن تمثيل الثابت باي π بعدد محدود من الأرقام العشرية decimal digits بعد الفاصلة، فإن كثيرًا من الأعداد تفقد دقتها عند تمثيلها بأربع وستين بِتّ فقط. ولكن لا يُمثِّل هذا مشكلةً إلا في حالات محددة. ومن المهم أن تكون على دراية بهذا، وتُعامِل الأعداد الكسرية معاملةً تقريبية، وليس على أنها قيم دقيقة. العمليات الحسابية العملية الحسابية هي العملية الأساسية المستَخدَمة مع الأعداد، وتأخذ المعاملات الحسابية arithmetic operations عددان، وتُنتِج عددًا جديدًا، مثل: الجمع، والضرب؛ وتُمثَّل هذه المعاملات في جافاسكربت، كما يأتي: 100 + 4 * 11 وتُسمّى الرموز + و* بالعوامل operators، فالعامل الأول هو عامل الجمع، والعامل الثاني هو عامل الضرب، ولدينا - للطرح، و / للقسمة، وبمجرّد وضع العامل بين قيمتين، تُنفَّذ العملية الحسابية وتَنتُج قيمة جديدة، ولكن هل يعني المثال السابق أن نضيف 4 إلى 100 ونضرب النتيجة في 11، أم أن الأولوية للضرب أولًا؟ لعلّك خمّنت أن الضرب أولًا، وهذا صحيح، لكن يمكنك تغيير هذا الترتيب مثل الرياضيات، وذلك بوضع عملية الجمع بين قوسين، مما يرفع من أولوية تنفيذها، كما يأتي: (100 + 4) * 11 ويُحدَّد ترتيب تنفيذ العوامل، عند ظهورها بدون أقواس، بأولوية تلك العوامل، فكما أن الضرب في المثال السابق له أولوية على الجمع، فللقسمة أولوية الضرب ذاتها، في حين يملك الجمع والطرح أولوية بعضهما، وتُنفَّذ العوامل بالترتيب من اليسار إلى اليمين، إذا كانت في رتبة التنفيذ نفسها، فمثلًا: إذا جاء الجمع والطرح معًا، فستكون الأولوية في التنفيذ لمن يبدأ من اليسار أولًا، أي كما في المثال التالي: 1 - 2 + 1 حيث تُنفَّذ العمليات من اليسار إلى اليمين، مثل عملية الطرح بين أقواس، أي هكذا: (1 - 2) + 1 ولا تقلق كثيرًا بشأن هذه الأولويات، فلو حدث ونسيت أولويةً ما، أو أردت تحقيق ترتيب معيّن، فضعه داخل أقواس وانتهى الأمر. لدينا عامل حسابي آخر قد لا تميّزه للوهلة الأولى، وهو الرمز %، والذي يُستخدَم لتمثيل عملية الباقي remainder، فيكون X % Y هو باقي قسمة X على Y، فمثلًا: نتيجة 314 % 100 هي 14، أما نتيجة 144 % 12 فتساوي 0. وأولوية عامل الباقي هي الأولوية ذاتها للضرب والقسمة، ويُشار عادةً إلى هذا العامل باسم modulo. الأعداد الخاصة لدينا ثلاثة قيم خاصة في جافاسكربت، ننظر إليها على أنها أعداد، ولكنها لا تُعَدّ أعدادًا طبيعية. وأول قيمتين هما: infinity، و-infinity، وتُمثِّلان اللانهاية بموجبها وسالبها، وبالمثل، فإن infinity -1 لا تزال تشير إلى اللانهاية. ولا تثق كثيرًا بالحسابات المبنيَّة على اللانهاية، لأنها ليست منطقيةً رياضيًا، وستقود إلى القيمة الخاصة التالية، وهي: NaN، والتي تُشير إلى "ليس عددًا" Not A Number، رغم كونه قيمةً من نوع عددي بذاته، وستحصل عليه مثلًا: إذا حاولت قسمة صفر على صفر، أو طرح لانهايتين، أو أيّ عدد من العمليات العددية التي لا تُنتِج قيمةً مفيدة. السلاسل النصية السلسلة النصية String هي النوع التالي من أنواع البيانات الأساسية، ويُستخدم هذا النوع لتمثيل النصوص، ويُمثَّل هذا النوع في جافاسكربت، بنص محاط بعلامات اقتباس، أي كالتالي: `Down on the sea` "Lie on the ocean" 'Float on the ocean' وتستطيع استخدام العلامة الخلفية `، أو علامات الاقتباس المفردة '، أو المزدوجة ''، لتحديد السلاسل النصية، طالما أن العلامة التي وضعتها في بداية السلسلة هي ذاتها الموجودة في نهايتها. وتُوضع تقريبًا جميع أنواع البيانات داخل علامات الاقتباس تلك، وستعاملها جافاسكربت على أنها سلسلة نصية، ولكن ستجد صعوبةً في التعامل مع بعض المحارف، فمثلًا: كيف تضع علامات اقتباس داخل علامات الاقتباس المحدِّدة للسلسلة النصية؟ وكذلك محرف السطر الجديد Newlines، وهو ما تحصل عليه حين تضغط زرّ الإدخال؟ ولكتابة هذه المحارف داخل سلسلة نصية، يُنفَّذ الترميز التالي: إذا وجدت شَرطةً مائلةً خلفيةً \ داخل نص مُقتَبس، فهذه تشير إلى أن المحرف الذي يليها، له معنى خاص، ويسمّى هذا تهريب المحرف Escaping the character؛ إذ لن تنتهي السلسلة النصية عند احتوائها على علامات الاقتباس المسبوقة بشرطة مائلة خلفية، بل ستكون جزءًا منها؛ وحين يقع محرف n بعد شرطة مائلة خلفية فإنه يُفسَّر على أنه سطر جديد، وبالمِثل، فإذا جاء محرف t بعد شرطة مائلة خلفية، فإنه يعني محرف الجدولة tab، وtd مثال على ذلك، لدينا السلسلة النصية التالية: "هذا سطر\nوهذا سطر جديد" حيث سيبدو النص بعد تفسيره، كما يأتي: هذا سطر وهذا سطر جديد كما ستحتاج في بعض المواقف إلى وضع شرطة مائلة خلفية داخل السلسلة النصية، لتكون مجرّد شرطة مائلة \، وليست مِحرفًا خاصًّا، فإذا جاءت شرطتان مائلتان خلفيتان متتابعتان، فستلغيان بعضهما، بحيث تظهر واحدة منهما فقط في القيمة الناتجة عن السلسلة النصية. فمثلًا، تُكتَب السلسلة النصية التالية: "يُكتَب محرف السطر الجديد هكذا "\n"." في جافاسكربت، كما يأتي: "يُكتب محرف السطر الجديد هكذا \"\\n\"." وينطبق هنا ما ذكرناه سابقًا في شأن البِتّات وتخزين الأعداد، حيث يجب تخزين السلاسل النصية على هيئة بِتّات داخل الحاسوب. تُخزِّن جافاسكربت السلاسل النصية بناءً على معيار يونيكود Unicode، الذي يُعيِِّن عددًا لكل محرف تقريبًا قد تحتاجه ، بما في ذلك المحارف التي في اللغة العربية، واليونانية، واليابانية، والأرمنية، وغيرها. وتُمثَّل السلسلة النصية بمجموعة من الأعداد، بما أنه لدينا عدد لكل محرف، وهذا ما تفعله جافاسكربت تحديدًا، لكن لدينا مشكلة، فتمثيل جافاسكربت يستخدِم 16بت لكل عنصر من عناصر السلسلة النصية، ما يعني أنه لدينا 216 محرفًا مختلفًا، ولكن يُعرِّف اليونيكود أكثر من ذلك، أي بمقدار الضعف تقريبًا هنا، لذا تشغل بعض المحارف مثل الصور الرمزية emoji، موقعين من مواقع المحارف في سلاسل جافاسكربت النصية، وسنعود لهذا مرةً أخرى في الفصل الخامس. ولا يمكن تقسيم السلسلة النصية أو ضربها أو الطرح منها، لكن يمكن استخدام عامل + عليها، حيث لا يضيف بعضها إلى بعض كما تتوقّع من +، وإنما يجمعها إلى بعضها ويسلسلها معًا، أو يلصق إن صحّ التعبير بعضها ببعض، فمثلًا، سينتج السطر التالي، كلمة "concatenate": "con" + "cat" + "e" + "nate" تملك القيم النصية عددًا من الدوال المصاحبة لها -التوابع methods- التي تُستخدَم لإجراء عمليات أخرى عليها، وسنذكُر هذا بمزيد من التفصيل في الفصل الرابع. حيث تتصرّف السلاسل النصية المحاطة بعلامات اقتباس مفردة أو مزدوجة تصرّفًا متشابهًا تقريبًا، والاختلاف الوحيد بينهما هو نوع الاقتباس الذي تحتاج تهريبه داخلها. أما السلاسل المحاطة بعلامة خلفية (`)، والتي تُسمّى عادةً بالقوالب المجرّدة template literals، فيمكن تنفيذ عمليات إضافية عليها، مثل الأسطر الجديدة التي ذكرناها، أو تضمين قيم أخرى، كما في المثال التالي: `half of 100 is ${100 / 2}` حين تكتب شيئًا داخل {}$ في قالب مجرّد، ستُحسب نتيجته، ثم تُحوَّل هذه النتيجة إلى سلسلة نصية وتُدمَج في ذلك الموضع، وعليه يخرج المثال السابق "half of 100 is 50". العوامل الأحادية تُكتَب بعض العوامل على هيئة كلمات، فليست كلها رموزًا، وأحد الأمثلة على ذلك هو عامل typeof، والذي يُنتِج قيمةً نصيةً تُمثِّل اسم نوع القيمة الممررة إليه. انظر الشيفرة التالية، تستطيع تعديلها وتشغيلها في طرفية المتصفِّح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. console.log(typeof 4.5) // → number console.log(typeof "x") // → string استخدمنا console.log في المثال التوضيحي السابق، لبيان أننا نريد أن نرى نتيجة تقييم شيء ما، وسنبيُّن ذلك لاحقًا في الفصل التالي. وتُنفَّذ العوامل التي بيّناها في هذا الفصل اعتمادًا على قيمتين، لكن العامل typeof يأخذ قيمةً واحدةً فقط، وتُسمّى العوامل التي تستخدم قيمتين، بالعوامل الثنائية binary operators، أما تلك التي تأخذ عاملًا واحدًا فقط، فتسمى العوامل الأحادية unary operators، مع ملاحظة أن عامل الطرح - يمكن استخدامه كعامل أحادي أو ثنائي، كما في المثال التالي: console.log(- (10 - 2)) // → -8 القيم البوليانية حين يكون لدينا احتمالان، فمن المفيد إيجاد قيمة تفرّق بين الاحتمالين، مثل: "yes" و "no"، أو "on" و "off"، وتِستخدِم جافاسكربت النوع البولياني Boolean لهذا الغرض، ويتكون هذا النوع من قيمتين فقط، هما: القيمة true والقيمة false، وتُكتبان بهاتين الكلمتين فقط. الموازنة انظر الطريقة التالية لإنتاج قيم بوليانية: console.log(3 > 2) // → true console.log(3 < 2) // → false علامتي <، و> هما اللتان تعرفهما من الرياضيات للإشارة إلى الموازنة "أصغر من"، أو "أكبر من"، وكلاهما عاملان ثنائيّان، ويُنتِجان قيمةً بوليانيةً تُوضِّح هل الشرط مُتحقِق أم لا، ويمكن موازنة السلاسل النصية بالطريقة نفسها، كما في المثال التالي: console.log("Aardvark" < "Zoroaster") // → true تُعَدّ الطريقة التي تُرتَّب بها السلاسل النصية أبجدية في الغالب، لكن على خلاف ما قد تراه في القاموس، تكون الحروف الكبيرة أقل من الحروف الصغيرة، فمثلًا، Z أقل من a، والمحارف غير الأبجدية (!، -، …إلخ) مدمجة أيضًا في الترتيب، وتمر جافاسكربت على المحارف من اليسار إلى اليمين موازِنةً محارف يونيكود واحدًا تلو الآخر. والعوامل الأخرى التي تُستخدَم في الموازنة هي: <= (أقل من أو يساوي)، و =< (أكبر من أو يساوي)، و == (يساوي)، و=! (لا يساوي). console.log("Itchy" != "Scratchy") // → true console.log("Apple" == "Orange") // → false وتوجد قيمة واحدة في جافاسكربت لا تساوي نفسها، وهي NaN بمعنى "ليس عددًا"، أي كما يأتي: console.log(NaN == NaN) // → false وبما أن NaN تشير إلى نتيجة عملية حسابية غير منطقية، فهي لن تساوي أيّ نتيجة أخرى لحساب غير منطقي. العوامل المنطقية كذلك لدينا في جافاسكربت بعض العوامل التي قد تُطبَّق على القيم البوليانية نفسها، وتدعم جافاسكربت ثلاثةً منها، وهي: and، وor، وnot، ويمكن استخدامها في منطق القيم البوليانية. ويُمثَّل عامل "and" بالرمز &&، وهو عامل ثنائي نتيجته صحيحة true إن كانت القيمتان المعطتان صحيحتان معًا. console.log(true && false) // → false console.log(true && true) // → true أما عامل الاختيار "or"، فيُمثَّل بالرمز ||، ويُخرِج true إذا تحققت صحة إحدى القيمتين أو كليهما، كما في المثال التالي: console.log(false || true) // → true console.log(false || false) // → false أما "Not" فتُكتب على صورة تعجب !، وهي عامل أحادي يقلب القيمة المعطاة له، فالصحيح المتحقِّق منه true! يَخرج لنا خطأً غير متحقِّق false، والعكس بالعكس. وعند دمج هذه العوامل البوليانية مع العوامل الحسابية والعوامل الأخرى، فلن نستطيع تَبيُّن متى نضع الأقواس في كل حالة أو متى نحتاج إليها، والحل هنا يكون بالعلم بحال العوامل التي ذكرناها حتى الآن لشق طريقك في البرامج التي تكتبها، والشيفرات التي تقرؤها، إذ أن عامل الاختيار || هو أقل العوامل أولوية، ثم يليه عامل &&، ثم عوامل الموازنة (<، ==، …إلخ)، ثم بقية العوامل، واختيرت هذه الأسبقية أو الأولوية، كي يقل استخدام الأقواس إلى أدنى حد ممكن، انظر المثال التالي: 1 + 1 == 2 && 10 * 10 > 50 والعامل الأخير الذي لدينا ليس أحاديًّا ولا ثنائيًّا، بل i; عامل ثلاثي يعمل على ثلاث قيم، ويُكتب على صورة علامة استفهام ?، ثم نقطتين رأسيّتين :، أي على الصورة التالية: console.log(true ? 1 : 2); // → 1 console.log(false ? 1 : 2); // → 2 ويُسمّى هذا العامل بالعامل الشرطي، أو العامل الثلاثي بما أنه الثلاثيُّ الوحيد في جافاسكربت، وتُحدِّد القيمة التي على يسار علامة الاستفهام، نتيجة أو خرْج هذا العامل، لتكون النتيجة هي إحدى القيمتين الأخرتين، فإذا كانت هذه القيمة true فالخرج هو القيمة الوسطى، وإن كانت false فالنتيجة هي القيمة الأخيرة التي على يمين النقطتين الرأسيّتين. القيم الفارغة يوجد في جافاسكربت قيمتان خاصتان تُكتبان على الصيغة null، وundefined، وتُستخدمان للإشارة إلى قيمة لا معنى لها، أو غير مفيدة، وهما قيمتان في حد ذاتهما، لكنهما لا تحملان أيّ بيانات، وستجد عمليات عدّة في هذه اللغة لا تُنتِج قيمةً ذات معنى كما سترى لاحقًا، لكنها ستُخرج القيمة undefined لأنها يجب أن تُخرِج أيّ قيمة. ولا تشغل نفسك بالاختلاف بين undefined، وnull، فهما نتيجة أمر عارض أثناء تصميم جافاسكربت، ولا يهم غالبًا أيّ واحدة ستختار منهما، لذا عاملهما على أنهما قيمتان متماثلتان. التحويل التلقائي للنوع ذكرنا في المقدمة أن جافاسكربت تقبل أيَّ برنامج تعطيه إياها، حتى البرامج التي تُنفِّذ أمورًا غريبة، وتوضح التعبيرات التالية هذا المفهوم: console.log(8 * null) // → 0 console.log("5" - 1) // → 4 console.log("5" + 1) // → 51 console.log("five" * 2) // → NaN console.log(false == 0) // → true وحين يُطبَّق عامل ما على النوع الخطأ من القيم، فستُحوِّل جافاسكربت تلك القيمة إلى النوع المطلوب باستخدام مجموعة قواعد قد لا تريدها أو تتوقعها، ويسمّى ذلك تصحيح النوع القسري type coercion. إذ تُحوِّل null في التعبير الأول من المثال السابق إلى 0، وتُحوَّل "5" إلى 5 أي من سلسلة نصية إلى عدد، أما في التعبير الثالث الذي يحوي عامل الجمع + بين نص وعدد، فنفّذت جافاسكربت الربط Concatenation قبل الإضافة العددية، وحوّلت 1 إلى "1" أي من عدد إلى نص. أما عند تحويل قيمة لا تُعبِّر بوضوح على أنها عدد إلى عدد، مثل:"five" أو undefined، فسنحصل على NaN، ولذا فإن حصلت على هذه القيمة في مثل هذا الموقف، فابحث عن تحويلات نوعية من هذا القبيل. كذلك حين نوازن قيمتين من النوع نفسه باستخدام ==، فسيسهل توقّع الناتج، إذ يجب أن تحصل على true عند تطابق القيمتين إلا في حالة NaN، أما حين تختلف القيم، فتَستخدِم جافاسكربت مجموعة معقدّة من القواعد لتحديد الإجراء الذي يجب تنفيذه، وتحاول في أغلب الحالات أن تحوّل قيمةً أو أكثر إلى نوع القيمة الأخرى. لكن حين تكون إحدى القيمتين null، أو undefined، فستكون النتيجة تكون صحيحةً فقط إذا كان كل من الجانبين null أو undefined. كما في المثال التالي: console.log(null == undefined); // → true console.log(null == 0); // → false وهذا السلوك مفيد حين تريد اختبار أيُّ القيم فيها قيمةً حقيقيةً بدلًا من null أو undefined، فتوازنهما بعامل == أو =!. لكن إن أردت اختبار شيئ يشير إلى قيمة بعينها مثل false، فإن التعبيرات مثل 0 == false و" " == false تكون صحيحةً أيضًا، وذلك بسبب التحويل التلقائي للنوع، أما إذا كنت لا تريد حدوث أيّ تحويل نوعي، فاستخدم هذين العاملَيْن: ===، و ==!. حيث يَنظر أول هذين العاملَين هل القيمة مطابقة للقيمة الثانية المقابلة أم لا، والعامل الثاني ينظر أهي غير مطابقة أم لا، وعليه يكون التعبير " " === false خطأ كما توقعت. وإني أنصح باستخدام العامل ذي المحارف الثلاثة تلقائيًّا، وذلك لتجنُّب حدوث أي تحويل نوعي يعطِّل عملك، لكن إن كنت واثقًا من الأنواع التي على جانبي العامل، فليس هناك ثمة مشكلة في استخدام العوامل الأقصر. قصر العوامل المنطقية يعالج العاملان && و|| القيم التي من أنواع مختلفة، معالجةً غريبة، إذ يحوِّلان القيمة التي على يسارهما إلى نوع بولياني لتحديد ما يجب فعله، لكنهما يعيدان إما القيمة الأصلية للجانب الأيسر أو قيمة الجانب الأيمن، وذلك وفقًا لنوع العامل، ونتيجة التحويل للقيمة اليسرى، سيُعيد عامل || مثلًا قيمة جانبه الأيسر إذا أمكن تحويله إلى true، وإلا فسيعيد قيمة جانبه الأيمن. يُحدِث هذا النتيجةَ المتوقّعة إن كانت القيم بوليانية، ونتيجةً مشابهةً إن كانت القيم من نوع آخر. كما في المثال الآتي: console.log(null || "user") // → user console.log("Agnes" || "user") // → Agnes نستطيع استخدام هذا السلوك على أنه طريقة للرجوع إلى القيمة الافتراضية، فإن كانت لديك قيمة قد تكون فارغةً، فيمكنك وضع || بعدها مع قيمة بدل، حيث إذا كان من الممكن تحويل القيمة الابتدائية إلى false فستحصل على البدل. وتنص قواعد تحويل النصوص والأعداد، إلى قيم بوليانية، على أن 0، وNaN، والنص الفارغ " "، جميعها خطأً false، بينما تُعَدّ القيم الأخرى true، لذا فإن 0 || -1 تخرج 1-، و " " || "!?" تخرج "?!". ويتصرّف عامل && تصرّفًا قريبًا من ذلك، ولكن بطريقة أخرى، فإذا كان من الممكن تحويل القيمة اليسرى إلى false فسعيد تلك القيمة، وإلا سيعيد القيمة التي على يمينه. وهذان العاملان لهما خاصيّةً أخرى مُهمة، وهي أن الجزء الذي على يمينهما يُقيَّم عند الحاجة فقط، ففي حالة true || x ستكون النتيجة القيمة true مهما كانت قيمة x، حتى لو كانت جزءًا من برنامج يُنفِّذ شيئًا مستَهجنًا، بحيث لا تُقيَّم x عندها، ويمكن قول الشيء نفسه فيما يخص false && x والتي ستعيد القيمة false دومًا وتتجاهل x. ويسمّى هذا بالتقييم المقصور Short-circuit Evaluation. إذ يتصرَّف العامل الشرطي تصرّفًا قريبًا من ذلك، فالقيمة المختارة من بين القيم الثلاثة هي التي تُقيَّم فقط. خاتمة اطلعنا في هذا الفصل على أربعة أنواع من قيم جافاسكربت، وهي: الأرقام، والسلاسل النصية، والقيم البوليانية، والغير معرَّفة، حيث تُنشَأ هذه القيم بكتابة اسمها، كما في: true، و null، أو قيمتها، كما في: 13، و"abc"، وتُحوَّل وتُجمَع هذه القيم باستخدام عوامل أحادية، أو ثنائية، أو ثلاثية. كما رأينا عوامل حسابية، مثل: +، و-، و*، و/، و%، وعامل الضم النصي +، وعوامل الموازنة، وهي: ==، و =!، و===، و==!، و>، و<، و=>، و=<، والعوامل المنطقية، وهي:&&، و||، إلى جانب تعرُّفنا على عدّة عوامل أحادية، مثل: -، الذي يجعل العدد سالبًا، أو !، المُستخدَم في النفي المنطقي، وtypeof لإيجاد نوع القيمة، وكذلك العامل الثلاثي :? الذي يختار إحدى القيمتين وفقًا لقيمة ثالثة. ويعطيك ما سبق ذكره بيانات كافيةً لتستخدم جافاسكربت على أساس حاسبة جيب صغيرة، وفي الفصل التالي، سنبدأ بربط هذه التعبيرات لنكتب برامج بسيطة بها. ترجمة -بتصرف- للفصل الأول من كتاب Elequent Javascript لصاحبه Marijn Haverbeke. اقرأ أيضًا المقال التالي: هيكل البرنامج في جافاسكريبت الدوال العليا في جافاسكريبت1 نقطة
-
يقول دونالد كنوث Donald Knuth لا غنى عن الدوال في لغة جافاسكربت، إذ نستخدمها في هيكلة البرامج الكبيرة لتقليل التكرار، ولربط البرامج الفرعية بأسماء، وكذا لعزل تلك البرامج الفرعية عن بعضها، ولعل أبرز تطبيق على الدوال هو إدخال مصطلحات جديدة في اللغة. حيث يمكن إدخال أيّ مصطلح إلى لغة البرمجة من أيّ مبرمج يعمل بها، وذلك على عكس لغات البشر المنطوقة التي يصعب إدخال مصطلحات إليها، إلا بعد مراجعات واعتمادات من مجامع اللغة. وفي الواقع المشاهد، يُعَدّ إدخال المصطلحات إلى اللغة على أساس دوال، ضرورةً حتميةً لاستخدامها في البرمجة وإنشاء برامج للسوق. فمثلًا، تحتوي اللغة الإنجليزية -وهي المكتوب بحروفها أوامر لغات البرمجة-، على نصف مليون كلمة تقريبًا، وقد لا يعلم المتحدث الأصلي لها إلا بـ 20 ألف كلمة منها فقط، وقَلَّ ما تجد لغةً من لغات البرمجة التي يصل عدد أوامرها إلى عشرين ألفًا. وعليه، ستكون المصطلحات المتوفرة فيها دقيقة المعنى للغاية، وبالتالي فهي جامدة وغير مرنة، ولهذا نحتاج إلى إدخال مصطلحات جديدة على هيئة دوال، وذلك بحسب حاجة كل مشروع أو برنامج. تعريف الدالة الدالة هي رابطة منتظمة، حيث تكون قيمة هذه الرابطة هي الدالة نفسها، إذ تُعرِّف الشيفرة التالية مثلًا، الثابت square لتشير إلى دالة تنتج مربع أي عدد مُعطَى: const square = function(x) { return x * x; }; console.log(square(12)); // → 144 وتُنشأ الدالة بتعبير يبدأ بكلمة function المفتاحية، كما يكون للدوال مجموعة معامِلات parameters -معامِل وحيد هو x حسب المثال السابق-، ومتن body لاحتواء التعليمات التي يجب تنفيذها عند استدعاء الدالة، كما يُغلَّف متن الدالة بقوسين معقوصين حتى ولو لم يكن فيه إلا تعليمة واحدة. كذلك يجوز للدالة أن يكون لها عدة معامِلات، أو لا يكون لها أيّ معامِل، ففي المثال التالي، لا تحتوي دالة makenoise على أيّ معاملات، بينما تحتوي power على معاملين اثنين: const makeNoise = function() { console.log("Pling!"); }; makeNoise(); // → Pling! const power = function(base, exponent) { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; }; console.log(power(2, 10)); // → 1024 وتنتج بعض الدوال قيمًا، مثل: دالتي power، وsquare، ولكن هذا ليس قاعدة، إذ لا تعطي بعض الدوال الأخرى قيمةً، مثل دالة makenoise، ونتيجتها الوحيدة هي أثر جانبي side effect. تحدِّد تعليمة return القيمة التي تعيدها الدالة، فحين تمر بُنية تحكُّم control -مثل التعليمات الشرطية- على تعليمة مشابهة لهذه، فستقفز مباشرةً من الدالة الحالية، وتعطي القيمة المعادة إلى الشيفرة التي استدعت الدالة. وإن لم يتبع كلمة return المفتاحية أيّ تعبير، فستعيد الدالة قيمة غير معرفة undefined، كما تعيد الدوال التي ليس فيها تعليمة return قيمة غير معرفة undefined، مثل دالة makenoise. تتصرف معامِلات الدالة على أساس الرابطات المنتظمة regular bindings، غير أنّه يحدِّد مستدعي الدالة قيمتها الأولية، وليس الشيفرة التي بداخل الدالة. الرابطات Bindings والنطاقات Scopes نطاق الرابطة في البرنامج هو الجزء الذي تكون الرابطة ظاهرةً فيه، حيث كل رابطة لها نطاق. وإذا عرَّفنا الرابطة خارج دالة أو كتلة شيفرات، فيكون نطاق هذه الرابطة البرنامج كاملًا، ويمكنك الإشارة إلى مثل تلك الرابطات أينما تشاء، وتسمى رابطات عامة Global Bindings؛ أما الرابطات المنشأة لمعامِلات الدالة، أو المصرح عنها داخل دالة ما، فيمكن الإشارة إليها داخل تلك الدالة فقط، وعليه تسمّى رابطات محلية Local bindings، وتُنشأ نسخ جديدة من تلك الرابطات في كل مرة تُستدعَى الدالة فيها، وذلك يوفر نوعًا من العزل بين الدوال بما أنّ كل دالة تتصرف في عالمها الخاص -بيئتها المحلية-، وييسّر فهم المراد منها دون الحاجة إلى العلم بكل ما في البيئة العامة. كما تكون الرابطات المصرح عنها باستخدام let، وconst رابطات محلية لكتلة الشيفرة التي صُرح عن تلك الرابطات فيها، فإن أنشأت أحد تلك الرابطات داخل حلقة تكرارية، فلن تتمكن الشيفرات الموجودة قبل هذه الحلقة وبعدها، من رؤية تلك الرابطة. ولم يُسمح إنشاء نطاقات جديدة لغير الدوال في إصدارات جافاسكربت قبل 2015، لذا كانت الرابطات التي أُنشِئت باستخدام كلمة var المفتاحية، مرئيةً في كل الدالة التي تظهر فيها هذه الرابطات، أو في النطاق العام إن لم تكن داخل دالة ما. كما في المثال التالي: let x = 10; if (true) { let y = 20; var z = 30; console.log(x + y + z); // → 60 } // y is not visible here console.log(x + z); // → 40 يستطيع كل نطاق البحث في النطاق الذي يحيط به، لذا تكون x ظاهرة داخل كتلة الشيفرة في المثال السابق مع استثناء وجود عدة رابطات بالاسم نفسه، ففي تلك الحالة لا تستطيع الشيفرة إلا رؤية الأقرب لها، كما في المثال التالي، حيث تشير الشيفرة داخل دالة halve إلى n الخاصة بها وليس إلى n العامة: const halve = function(n) { return n / 2; }; let n = 10; console.log(halve(100)); // → 50 console.log(n); // → 10 النطاق المتشعب نستطيع إنشاء كتل شيفرات ودوال داخل كتل ودوال أخرى ليصبح لدينا عدة مستويات من المحلية، فمثلًا، تخرج الدالة التالية المكونات المطلوبة لصنع مقدار من الحمُّص، وتحتوي على دالة أخرى داخلها، أي كما يأتي: const hummus = function(factor) { const ingredient = function(amount, unit, name) { let ingredientAmount = amount * factor; if (ingredientAmount > 1) { unit += "s"; } console.log(`${ingredientAmount} ${unit} ${name}`); }; ingredient(1, "can", "chickpeas"); ingredient(0.25, "cup", "tahini"); ingredient(0.25, "cup", "lemon juice"); ingredient(1, "clove", "garlic"); ingredient(2, "tablespoon", "olive oil"); ingredient(0.5, "teaspoon", "cumin"); }; تستطيع شيفرة الدالة ingredient أن ترى رابطة factor من الدالة الخارجية، على عكس رابطتيها المحليتين الغير مرئيتين من الدالة الخارجية، وهما: unit، وingredientAmount. ويُحدِّد مكان كتلة الشيفرة في البرنامج الرابطات التي ستكون مرئيةً داخل تلك الكتلة، حيث يستطيع النطاق المحلي رؤية جميع النطاقات المحلية التي تحتويه، كما تستطيع جميع النطاقات رؤية النطاق العام، ويُسمّى هذا المنظور لمرئية الرابطات، المراقبة المُعجَمية Lexical Scoping. الدوال على أساس قيم تتصرف رابطة الدالة عادةً على أساس اسم لجزء بعينه من البرنامج، وتُعرَّف هذه الرابطة مرةً واحدةً ولا تتغير بعدها، ويسهّل علينا هذا، الوقوع في الخلط بين اسم الدالة والدالة نفسها، غير أنّ الاثنين مختلفان عن بعضهما، إذ تستطيع قيمة الدالة فعل كل ما يمكن للقيم الأخرى فعله، كما تستطيع استخدامها في تعبيرات عشوائية، وتخزينها في رابطة جديدة، وتمريرها كوسيط لدالة، وهكذا. وذلك إضافةً إلى إمكانية استدعاء تلك القيمة بلا شك. وبالمثل، لا تزال الرابطة التي تحمل الدالة مجرد رابطة منتظمة regular bindung، كما يمكن تعيين قيمة جديدة لها إذا لم تكن ثابتة constant، كما في المثال الآتي: let launchMissiles = function() { missileSystem.launch("now"); }; if (safeMode) { launchMissiles = function() {/* لا تفعل شيئًا */}; } وسنناقش في المقال الخامس بعض الأمور الشيقة التي يمكن فعلها بتمرير قيم الدالة إلى دوال أخرى. مفهوم التصريح توجد طريقة أقصر لإنشاء رابطة للدالة، حيث تُستخدم كلمة function المفتاحية في بداية التعليمة، أي كما يلي: function square(x) { return x * x; } ويسمى هذا بتصريح الدالة function declaration، فتعرِّف التعليمة الرابطة "square" وتوجهها إلى الدالة المعطاة، وذلك أسهل قليلًا في الكتابة، ولا يتطلب فاصلة منقوطة بعد الدالة، لكن قد يكون هذا الأسلوب من التصريح عن الدوال خدّاعًا: console.log("يقول لنا المستقبل", future()); function future() { return "لن تكون هناك سيارات تطير"; } وعلى الرغم من أن الدالة معرَّفة أسفل الشيفرة التي تستخدمها، إلا أنها صالحة وتعمل بكفاءة، وذلك لأن تصريح الدوال ليس جزءًا من مخطط السير العادي من الأعلى إلى الأسفل، بل يتحرك إلى قمة نطاقه، ويكون متاحًا للاستخدام من قِبَل جميع الشيفرات الموجودة في ذلك النطاق، ويفيدنا هذا أمر أحيانًا لأنه يوفر حرية ترتيب الشيفرة ترتيبًا منطقيًا ومفيدًا، دون القلق بشأن الحاجة إلى تعريف كل الدوال قبل استخدامها. الدوال السهمية Arrow Functions لدينا مفهوم ثالث للتصريح عن الدوال، وقد يبدو مختلفًا عن البقية، حيث يستخدِم سهمًا مكتوبًا في صورة إشارة التساوي ومحرف "أكبر من"، أي على الصورة (=>)، لهذا انتبه من الخلط بينها وبين محرف "أكبر من أو يساوي"، الذي يُكتب على الصورة (>=)، ويوضح المثال التالي هذا المفهوم: const power = (base, exponent) => { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; }; يأتي السهم بعد قائمة المعامِلات ويُتبع بمتن الدالة، ويكون على صورة: "هذا الدخل (المعامِلات) يُنتِج هذا الخرج (المتن)"، وحين يكون لدينا اسم معامِل واحد، فيمكنك إهمال الأقواس المحيطة بقائمة المعامِلات، وإن كان المتن تعبيرًا واحدًا بدلًا من كتلة بين قوسين، فستعيد الدالة ذلك التعبير، وعليه ينفذ التعريفين التاليين لـ square، الشيء نفسه: const square1 = (x) => { return x * x; }; const square2 = x => x * x; وعندما تكون الدالة السهمية بدون معامِلات على الإطلاق، فستكون قائمة معامِلاتها مجرد قوسين فارغين، أي كما في المثال التالي: const horn = () => { console.log("Toot"); }; ليس ثمة سبب لوجود الدوال السهمية وتعبيرات function معًا في اللغة، إذ يملكان الوظيفة نفسها بصرف النظر عن التفاصيل الصغيرة، وسنتحدث عن ذلك في المقال السادس، كما لم تُضَف الدوال السهمية إلا في عام 2015، وذلك من أجل السماح بكتابة تعبيرات دوال صغيرة بأسلوب قليل الصياغة، حيث سنستخدمها كثيرًا في المقال الخامس. مكدس الاستدعاء The call stack قد تبدو طريقة تدفُق التحكم خلال الدوال متداخلة قليلا، انظر المثال التالي للتوضيح، حيث ينفذ بعض الاستدعاءات من الدوال المعطاة: function greet(who) { console.log("Hello " + who); } greet("Harry"); console.log("Bye"); وعند تشغيل البرنامج السابق فإن مخطط سيره يكون كالتالي: عند استدعاء greet، يقفز التحكم إلى بداية تلك الدالة (السطر الثاني في الشيفرة)، وتستدَعي بدورها console.log التي ينتقل التحكم إليها لتُنفّذ مهمتها، ثم تعود إلى المكان الذي استدعاها، وهو السطر الرابع. ثم يستدعي السطر الذي يليه، أي console.log مرةً أخرى، ويصل البرنامج إلى نهايته بعد إعادة ذلك. وإذا أردنا تمثيل مخطط تدفق التحكم لفظيًا، فسيكون كالتالي: خارج الدالة في greet في console.log في greet خارج الدالة في console.log خارج الدالة ونظرًا لوجوب قفز الدالة إلى المكان الذي استدعاها، فلابد للحاسوب من تذكُّر السياق الذي حدث منه الاستدعاء، ففي إحدى الحالات أعلاه، كان على console.log العودة إلى دالة greet عند انتهاء تنفيذها، بينما تعود إلى نهاية البرنامج في الحالة الأخرى. يسمى المكان الذي يخزن فيه الحاسوب هذا السياق، بمكدس الاستدعاء call stack، ويُخزَّن السياق الحالي في قمة ذلك المكدس في كل مرة تُستدعى دالة، كما تزيل السياق الأعلى من المكدس، وتستخدمه لمتابعة التنفيذ عندما تعود الدالة.، حيث يحتاج هذا المكدس إلى مساحة في ذاكرة الحاسوب، وبما أنّ تلك المساحة محدودة، فقد يعطيك الحاسوب رسالة فشل، مثل: عدم وجود ذاكرة كافية في المكدس "out of stack space"، أو تكرارات تفوق الحد المسموح به "too much recursion". حيث لدينا المثال الآتي: function chicken() { return egg(); } function egg() { return chicken(); } console.log(chicken() + " came first."); // → ?? إذ توضح الشيفرة السابقة هذا الأمر بسؤال الحاسوب أسئلة صعبة، تجعله يتنقّل بين الدالتين ذهابًا وإيابًا إلى ما لا نهاية، وفي حالة المكدس اللانهائي هذه، فستنفذ ذاكرة الحاسوب المتاحة، أو ستطيح بالمكدس blow the stack. الوسائط الاختيارية Optional arguments انظر الشيفرة التالية: function square(x) { return x * x; } console.log(square(4, true, "hedgehog")); // → 16 تسمح لغة جافاسكربت بتنفيذ الشيفرة السابقة دون أدنى مشكلة، ورغم أننا عرَّفنا فيها square بمعامِل واحد فقط، ثم استدعيناها بثلاثة معامِلات، فقد تجاهلت الوسائط الزائدة، وحسبت مربع الوسيط الأول فقط. وتستنتج من هذا أن جافاسكربت لديها سعة -إن صح التعبير- في شأن الوسائط التي تمررها إلى الدالة، فإن مررت وسائط أكثر من اللازم، فستُتجاهل الزيادة، أما إن مرّرت وسائط أقل من المطلوب، فتُسنَد المعامِلات المفقودة إلى القيمة undefined. وسيّئة ذلك أنك قد تُمرِّر عدد خاطئ من الوسائط، ولن تعرف بذلك، ولن يخبرك أحد ولا حتى جافاسكربت نفسها، أما حسنته فيمكن استخدام هذا السلوك للسماح لدالة أن تُستدعى مع عدد مختلف من الوسائط. انظر المثال التالي حيث تحاول دالة minus محاكاة معامِل - من خلال وسيط واحد أو وسيطين: function minus(a, b) { if (b === undefined) return -a; else return a - b; } console.log(minus(10)); // → -10 console.log(minus(10, 5)); // → 5 وإذا كتبنا عامل = بعد معامِل ما، ثم أتبعنا ذلك بتعبير، فستحل قيمة التعبير محل الوسيط إذا لم يكن معطى مسبقًا، إذ تجعل دالة الأس power مثلًا، وسيطها الثاني اختياريًا، فإن لم تعطها أنت ذلك الوسيط أو تمرر قيمة undefined، فسيتغير تلقائيًا إلى 2، وستتصرف الدالة مثل دالة التربيع square بالضبط، كما يأتي: function power(base, exponent = 2) { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; } console.log(power(4)); // → 16 console.log(power(2, 6)); // → 64 سننظر في المقال التالي إلى طريقة يحصل بها متن الدالة على جميع الوسائط الممررة، ويفيدنا هذا في السماح للدالة بقبول أي عدد من الوسائط، كما في console.log، إذ تُخرج كل القيم المعطاة إليها، أي: console.log("C", "O", 2); // → C O 2 التغليف Closure إذا قلنا أننا نستطيع معاملة الدوال مثل قيم، وأنه يعاد إنشاء الرابطات المحلية في كل مرة تُستدعى فيها الدالة، فإننا نتساءل هنا عما يحدث لتلك الرابطات حين يصير الاستدعاء الذي أنشأها غير نشط؟ توضح الشيفرة التالية مثالًا على هذا، فهي تعرِّف دالة wrapValue، والتي تنشئ رابطةً محليةً، ثم تعيد دالةً تصل إلى تلك الرابطة وتعيدها. انظر: function wrapValue(n) { let local = n; return () => local; } let wrap1 = wrapValue(1); let wrap2 = wrapValue(2); console.log(wrap1()); // → 1 console.log(wrap2()); // → 2 يُعَدّ هذا الأسلوب جائزًا ومسموحًا به في جافاسكربت، ولا يزال بإمكانك الوصول إلى كلا النسختين، حيث يوضح ذلك المثال حقيقة أنّ الرابطات المحلية تُنشَأ من جديد في كل استدعاء، وأنّ الاستدعاءات المختلفة لا تدمر رابطات بعضها البعض. وتسمّى تلك الخاصية بالمغلِّف closure، أي خاصية القدرة على الإشارة إلى نسخة بعينها من رابطة محلية في نطاق محيط enclosing scope، وتسمى الدالة التي تشير إلى رابطات من نطاقات محلية حولها، بالمغلف closure. يحررك هذا السلوك من القلق بشأن دورة حياة تلك الرابطات، ويتيح لك استخدام قيم الدوال بطرق جديدة، فيمكِّننا تغيير بسيط، من قلب المثال السابق إلى طريقة لإنشاء دوال تضاعِف بقيمة عشوائية، أي كما يلي: function multiplier(factor) { return number => number * factor; } let twice = multiplier(2); console.log(twice(5)); // → 10 وبما أنّ المعامِل نفسه يُعَدّ رابطةً محليةً، فلم نعد بحاجة إلى الرابطة الصريحة local من دالة wrapValue السابقة. ويحتاج التفكير في برامج مثل هذا إلى بعض التمرس، والنموذج الذهني المعين على هذا هو التفكير في قيم الدالة على أنها تحتوي شيفرة المتن وبيئتها التي أُنشئَت فيها، وحين تُستدعى الدالة، يرى متن الدالة البيئة التي أنشئت فيها وليس البيئة التي استدعيَت فيها. وفي المثال السابق، تُستدعى الدالة multiplier، وتُنشئ بيئة يكون فيها المعامل factor مقيدًا بـ 2، وتتذكر قيمة الدالة التي تعيدها، وتكون مخزنة في twice، هذه البيئة، لذا حين تُستدعى فستضاعف وسيطها بمقدار 2. التعاود Recursion تستطيع الدالة استدعاء نفسها طالما أنها لا تكثر من ذلك إلى الحد الذي يطفح المكدس، وتسمى هذه الدالة المستدعية نفسها باسم العودية recursive، حيث يسمح التعاود لبعض الدوال بأن تُكتب في صور مختلفة كما في المثال التالي، إذ نرى استخدامًا مختلفًا لدالة الأس power: function power(base, exponent) { if (exponent == 0) { return 1; } else { return base * power(base, exponent - 1); } } console.log(power(2, 3)); // → 8 وهذا قريب من الطريقة التي يُعرَّف بها الأس عند الرياضيين، ويصف الفكرة أفضل من الصورة التكرارية looping، إذ تستدعي الدالة نفسها عدة مرات مع أسس مختلفة، لتحقيق عمليات الضرب المتكررة. ولكن ثمة مشكلة في هذا النموذج، إذ هو أبطأ بثلاث مرات من الصورة التكرارية في تطبيقات جافاسكربت، فالمرور على حلقة تكرارية أيسر، وأقل تكلفةً من استدعاء دالة عدة مرات. وهذه المسألة، أي مسألة السرعة مقابل الأناقة، لَمعضلة فريدة بين ما يناسب الإنسان وما يناسب الآلة، فلا شك أننا نستطيع زيادة سرعة البرنامج إذا زدنا حجمه وتعقيده، وإنما يقع على المبرمج تقدير كل موقف ليوازن بين هذا وذاك. وإذا عدنا إلى حالة دالة الأس السابقة power، فأسلوب التكرار looping وهو المنظور غير الأنيق هنا، هو أبسط وأيسر في القراءة، وليس من المنطق استبدال النسخة التعاودية recursive به وإحلالها محله، لكن اعلم أنّ اختيار الأسهل، والأرخص، والأقل تكلفةً في المال والموارد الأخرى، ليس القاعدة في البرمجة، ولا يجب أن يكون كذلك، فقد يُعرض لنا موقف نتخلى فيه عن هذه الكفاءة من السهولة والسرعة في سبيل جعل البرنامج بسيطًا وواضحًا، وقد يكون فرط التفكير في الكفاءة مشتتًا لك عن المطلوب من البرنامج في الأصل، فهذا عامل آخر يعطل تصميمه، وبحسب المرء تعقيد البرنامج ومطلوب العميل منه، فلا داعي لإضافة عناصر جديدة تزيد القلق إلى حد العجز عن التنفيذ وإتمام العمل. لهذا أنصحك بمباشرة أول كتابتك للبرنامج بكتابة شيفرة صحيحة عاملة وسهلة الفهم، وهذا رأيي في ما يجب عليك وضعه كهدف نصب عينيك، وإن أردت تسريع البرنامج فتستطيع ذلك لاحقًا بقياس أدائه ثم تحسين سرعته إن دعت الحاجة، وإن كان القلق بشأن بطء البرنامج غالبًا ليس في محله بما أن أغلب الشيفرات لا تُنفَّذ بالقدر الذي يجعلها تأخذ وقتًا ملحوظًا. فقد تجد أحيانًا مشكلات يكون حلها أسهل باستخدام التعاود عوضًا عن التكرار، وهي المشاكل التي تتطلب استكشاف عدة فروع أو معالجتها، إذ قد تحتوي تلك الفروع بدورها على فروع أخرى، وهكذا تجد أنّ التكرار قد يكون أقل كفاءةً من التعاود أحيانًا! يمكنك النظر إلى الأحجية التالية كمثال على هذا، فإذا بدأنا من العدد 1 وأضفنا 5 أو ضربنا في 3 باستمرار ، فسينتج لدينا مجموعة لا نهائية من الأعداد. كيف تكتب دالةً نعطيها عددًا فتحاول إيجاد تسلسل عمليات الجمع والضرب التي تنتج هذا العدد؟ إرشاد: يمكن التوصل إلى العدد 13 بضرب 1 في 3، ثم إضافة 5 مرتين، في حين أننا لن نستطيع الوصول إلى العدد 15 مطلقًا. انظر الحل الآن بأسلوب التعاود: function findSolution(target) { function find(current, history) { if (current == target) { return history; } else if (current > target) { return null; } else { return find(current + 5, `(${history} + 5)`) || find(current * 3, `(${history} * 3)`); } } return find(1, "1"); } console.log(findSolution(24)); // → (((1 * 3) + 5) * 3) لاحظ أنّ هذا البرنامج لا يزعج نفسه بالبحث عن أقصر تسلسل من العمليات، بل أي تسلسل يحقق المراد وحسب، ولأن هذا البرنامج مثال رائع على أسلوب التفكير التعاودي، فسأعيد شرحه مفصلًا إن لم تستوعب منطقه بمجرد النظر. تنفذ دالة find الداخلية التعاود الحقيقي، فتأخذ وسيطين: العدد الحالي، وسلسلة نصية string لتسجل كيف وصلنا إلى هذا العدد، فإن وجدت حلًا، فستعيد سلسلةً نصيةً توضح كيفية الوصول إلى الهدف؛ أما إن لم تجد حلا بالبدء من هذا العدد، فستعيد null. ولتحقيق ذلك، تنفِّذ الدالة أحد ثلاثة إجراءات: يُعاد العدد الحالي إن كان هو العدد الهدف، حيث يُعَد السجل الحالي طريقة للوصول إليه. تُعاد null إن كان العدد الحالي أكبر من الهدف، فليس من المنطق أن نبحث في هذا الفرع، حيث ستجعل عملية الإضافة أو الضرب، العدد أكبر مما هو عليه. تُعاد النتيجة إن كنا لا نزال أقل من العدد الهدف، فتحاول الدالة كلا الطريقتين اللتين تبدءان من العدد الحالي باستدعاء نفسها مرتين، واحدة للإضافة وأخرى للضرب، وتُعاد نتيجة الاستدعاء الأول إن كان أي شيء غير null، وإلا فيُعاد الاستدعاء الثاني بغض النظر عن إخراجها لسلسلة نصية أم null. ولفهم كيفية إخراج هذه الدالة للأثر الذي نريده، دعنا ننظر في الاستدعاءات التي تُجرى على دالة find، عند البحث عن حل للعدد 13: find(1, "1") find(6, "(1 + 5)") find(11, "((1 + 5) + 5)") find(16, "(((1 + 5) + 5) + 5)") too big find(33, "(((1 + 5) + 5) * 3)") too big find(18, "((1 + 5) * 3)") too big find(3, "(1 * 3)") find(8, "((1 * 3) + 5)") find(13, "(((1 * 3) + 5) + 5)") found! لاحظ أنّ الإزاحة في المثال السابق توضح عمق مكدس الاستدعاء. حيث تستدعي find في أول استدعاء لها باستدعاء نفسها للبحث عن حل يبدأ بـ (1+5)، وسيتعاود هذا الاستدعاء للبحث في كل حل ينتج عددًا أقل أو يساوي العدد الهدف. وتعيد null إلى الاستدعاء الأول بما أنها لن تجد ما يطابق الهدف، وهنا يتدخل عامل || ليتسبب في الاستدعاء الذي يبحث في (1*3)، ويكون هذا البحث هو أول استدعاء تعاودي داخل استدعاء تعاودي آخَر يصيب العدد الهدف. ويعيد آخر استدعاء فرعي سلسلة نصية، وتُمرر هذه السلسلة من قبل عامليْ || في الاستدعاء البيني intermediate call، مما يعيد لنا الحل في النهاية. الدوال النامية Growing Functions لدينا في البرمجة طريقتين لإدخال الدوال في البرامج، أولاهما أن تجد نفسك تكرر كتابة شيفرة بعينها عدة مرات، وهو أمر لا شك أنك لا تريد فعله، فيزيد وجود شيفرات كثيرة من احتمال ورود أخطاء أكثر في البرنامج، ومن الإرهاق المصاحب في البحث عنها، ووقتًا أطول في قراءة الشيفرة منك ومن غيرك ممن يحاول فهم برنامجك لتعديله أو للبناء عليه، لذا عليك أخذ تلك الشيفرة المتكررة وتسميها باسم يليق بها ويعجبك، ثم تضعها في دالة. أما الطريقة الثانية فهي حين تحتاج إلى بعض الوظائف التي لم تكتبها بعد، ويبدو أنها تستحق دالة خاصة بها، فتبدأ بتسمية هذه الدالة، ثم تشرع في كتابة متنها، وقد تبدأ في كتابة التعليمات البرمجية التي تستخدم الدالة قبل تعريف الدالةَ نفسها. واعلم أنّ مقياس وضوح المفهوم الذي تريد وضعه في هذه الدالة، هو مدى سهولة العثور على اسم مناسب للدالة! فكلما كان هدف الدالة واضحًا ومحددًا، سهل عليك تسميتها. ولنقل أنك تريد كتابة برنامج لطباعة عددين: عدد الأبقار، وعدد الدجاج في مزرعة، مع إتباع العدد بكلمة بقرة، وكلمة دجاجة بعده، ووضع أصفار قبل كلا العددين بحيث يكون طولهما دائمًا ثلاثة خانات، فهذا يتطلب دالةً من وسيطين، وهما: عدد الأبقار، وعدد الدجاج. 007 Cows 011 Chickens وهذا يتطلب دالة من وسيطين، هما: عدد الأبقار، وعدد الدجاج. function printFarmInventory(cows, chickens) { let cowString = String(cows); while (cowString.length < 3) { cowString = "0" + cowString; } console.log(`${cowString} Cows`); let chickenString = String(chickens); while (chickenString.length < 3) { chickenString = "0" + chickenString; } console.log(`${chickenString} Chickens`); } printFarmInventory(7, 11); إذا كتبنا length. بعد تعبير نصي، فسنحصل على طول هذا التعبير، أو هذه السلسلة النصية، وعليه ستضيف حلقات while التكرارية أصفارًا قبل سلاسل الأعداد النصية، لتكون ثلاثة محارف على الأقل. وهكذا، فقد تمت مهمتنا! ولكن لنفرض أنّ صاحبة المزرعة قد اتصلت بنا قبيل إرسال البرنامج إليها، وأخبرتنا بإضافة اسطبل إلى مزرعتها، حيث استجلبت خيولًا، وطلبت إمكانية طباعة البرنامج لبيانات الخيول أيضًا. هنا تكون الإجابة أننا نستطيع، لكن خطر لنا خاطر بينما نحن نوشك على نسخ هذه الأسطر الأربعة، ونلصقها مرةً أخرى، إذ لا بد من وجود طريقة أفضل، أي كما يأتي: function printZeroPaddedWithLabel(number, label) { let numberString = String(number); while (numberString.length < 3) { numberString = "0" + numberString; } console.log(`${numberString} ${label}`); } function printFarmInventory(cows, chickens, horses) { printZeroPaddedWithLabel(cows, "Cows"); printZeroPaddedWithLabel(chickens, "Chickens"); printZeroPaddedWithLabel(horses, "Horses"); } printFarmInventory(7, 11, 3); وهنا نجحت الشيفرة، غير أنّ اسم printZeroPaddedWithLabel محرج نوعًا ما، إذ يجمع في وظيفة واحدة، بين كل من: الطباعة، وإضافة الأصفار، وإضافة العنوان label، لذا بدلًا من إلغاء الجزء المكرر من البرنامج. دعنا نختر مفهومًا واحدًا فقط: function zeroPad(number, width) { let string = String(number); while (string.length < width) { string = "0" + string; } return string; } function printFarmInventory(cows, chickens, horses) { console.log(`${zeroPad(cows, 3)} Cows`); console.log(`${zeroPad(chickens, 3)} Chickens`); console.log(`${zeroPad(horses, 3)} Horses`); } printFarmInventory(7, 16, 3); حيث تسهل الدالة ذات الاسم الجميل والواضح مثل zeroPad، على الشخص الذي يقرأ الشيفرة معرفة ما تفعله، وهي مفيدة في مواقف أكثر من هذا البرنامج خاصة، إذ تستطيع استخدامها لطباعة جداول منسقة من الأعداد. لكن إلى أي حد يجب أن تكون الدالة التي تكتبها ذكية، بل إلى أي حد يجب أن تكون متعددة الاستخدامات؟ اعلم أنك تستطيع عمليًا كتابة أي شيء بدءًا من دالة بسيطة للغاية، حيث تحشو عددًا ليكون بطول ثلاثة محارف، إلى نظام تنسيق الأعداد المعمم والمعقد، والذي يتعامل مع الأعداد الكسرية، والأعداد السالبة، ومحاذاة الفواصل العشرية، والحشو بمحارف مختلفة، وغير ذلك. والقاعدة هنا، هي ألا تجعل الدالة تزيد في وظيفتها عن الحاجة، إلا إذا تأكدت يقينًا من حاجتك إلى تلك الوظيفة الزائدة، فقد يكون من المغري كتابة "أُطر عمل" frameworks عامة لكل جزء من الوظائف التي تصادفها، لكنا نهيب بك ألا تستجيب لهذه الرغبة، إذ لن تنجز أيّ عمل حقيقي لأيّ عميل ولا لنفسك حتى، وإنما ستكتب شيفرات لن تستخدمها أبدًا. الدوال والآثار الجانبية يمكن تقسيم الدوال إلى تلك التي تُستدعَى لآثارها الجانبية side effects، وتلك التي تُستدعَى لقيمتها المعادة -رغم أنه قد يكون للدالة آثار جانبية، وقيم معادة في الوقت نفسه-، فالدالة الأولى هي دالة مساعدة في مثال المزرعة السابق، حيث تُستدعَى printZeroPaddedWithLabel لأثرها الجانبي، فتطبع سطرًا؛ أما النسخة الثانية zeroPad، فتُستدعى لقيمتها المعادة. ولا شك أنّ الحالة الثانية مفيدة أكثر من الأولى، فتكون الدوال التي تنشئ قيمًا، أسهل في إدخالها وتشكيلها في صور جديدة عن تلك التي تنتج آثارًا جانبية مباشرة. ولدينا من ناحية أخرى، دالةً تسمى بالدالة النقية pure function، وهي نوع خاص من الدوال المنتجة للقيم، حيث لا تحتوي على آثار جانبية، كما لا تعتمد على الآثار الجانبية من شيفرة أخرى، فمثلًا، لا تقرأ هذه الدوال الرابطات العامة global bindings التي قد تتغير قيمتها. ولهذا النوع من الدوال خاصية فريدة، إذ تنتج القيمة نفسها إن استُدعيَت بالوسائط نفسها، ولا تفعل أي شيء آخر، وإضافةً إلى ما سبق، ولا يتغير معنى الشيفرة إن أزلنا استدعاء الدالة ووضعنا مكانه القيمة التي ستعيدها. وإن حدث وشككت في عمل دالة نقية، فيمكنك اختبارها ببساطة عن طريق استدعائها، واعلم أنها إذا عملت في هذا السياق، فستعمل في أي سياق آخر، إذ تحتاج الدوال غير النقية إلى دعامات أخرى لاختبارها. لكن مع هذا، فلا داعي للاستياء عند كتابة دوال غير نقية، أو تنفيذ عمليات تطهير لحذفها من شيفراتك، فقد تكون الآثار الجانبية مفيدة، وهذا يحدث في الغالب من حالات البرمجة. فمثلًا، لا توجد طريقة لكتابة نسخة نقية من console.log، ونحن نحتاج هذه الدالة أيما احتياج، كما سترى أثناء تمرسك في جافاسكربت لاحقًا، كذلك تسهل الآثار الجانبية من التعبير عن بعض العمليات بطريقة فعالة، لذا قد تكون الحاجة للسرعة سببًا لتجنب هذا النقاء في الدوال. خاتمة اطلعنا في هذا المقال على كيفية كتابة الدوال البرمجية التي تحتاجها عند تنفيذ مهمة، أو وظيفة متكررة في برامجك، وذلك باستخدام كلمة function المفتاحية التي تستطيع إنشاء قيمة دالة إذا استُخدمت على أساس تعبير؛ أما إذا استُخدمت على أساس تعليمة، فتكون للإعلان عن رابطة binding، وإعطائها دالة تكون قيمةً لها؛ كما نستطيع إنشاء الدوال أيضًا باستخدام الدوال السهمية. يُعَدّ أحد الجوانب الرئيسية في فهم الدوال هو فهم النطاقات، حيث تنشئ كل كتلة نطاقًا جديدًا، وتكون المعامِلات والرابطات المصرَّح عنها في نطاق معين محلية وغير مرئية من الخارج. كما تتصرف الرابطات المصرَّح عنها بـ var تصرفًا مختلفًا، حيث ينتهي بهم الأمر في أقرب نطاق دالي أو في النطاق العام. واعلم أنّ فصل المهام التي ينفذها برنامجك إلى دوال مختلفة يفيدك في انتفاء الحاجة إلى التكرار الزائد عن الحد، وسترى أنّ الدوال مفيدة في تنظيم البرنامج، إذ تجمع تجميع الشيفرة في أجزاء تنفذ أشياءً محددة. ترجمة -بتصرف- للفصل الثالث من كتاب Elequent Javascript لصاحبه Marijn Haverbeke.1 نقطة
-
إذا كانت المهمة مهمة توقع كما أشرت، فإنه يتم استخدام MLPRegressor و هو نموذج للتوقع باستخدام الشبكات العصبونية يتم استخدامه عبر الموديول: neural_network.MLPRegressor مثل أي نموذج في التعلم الآلي يوجد لديه العديد من المعاملات التي تلعب دورا أساسيا في عملية تعلم الموديل عبر داتا التدريب لنقوم بالمرور على أهم المعاملات التي يأخذها هذا النموذج #استدعاء المكتبة: from sklearn.neural_network import MLPRegressor في البداية قمنا باستدعاء المكتبة التي يوجد فيها هذا الموديل #الشكل العام للموديل: MLPRegressorModel = MLPRegressor(activation='tanh', solver='adam', learning_rate='constant', early_stopping= False, alpha=0.0001 ,hidden_layer_sizes=(100, 3)) البارمتر الأول activation مثلما نعرف يوجد في الشبكات العصبونية عدة أنواع لتوابع التنشيط أو activation ومن أهمها تابع sigmoid , relu,tanh لن أدخل في تفاصيل كل منها فأي دورة تعلم الآلة أو تعلم عميق تحوي هذه المفاهيم ولكن كنصيحه نقوم بجعل relu لجميع الطبقات ماعدا الأخيره أما الطبقة الأخيره نستخدم sigmod البارمتر الثاني solver هو طريقة الحل أو طريقة الوصول إلى أفضل قيم w,b الأوزران الخاصه بالشبكه العصبونية يوجد أكثر من طريقه مثل sgd ,adam ولكن ننصح باستخدام adam دوما البارمتر الثالث learning_rate هو معامل التعلم وهو يمثل مقدار الخطوه للوصول إلى الأوزران ويمكن تركه costant أي خطوات ثابتة أو adaptive متغيره أما ان تكون طويله أو قصيرة البارمتر الرابع early_stopping التوقف المبكر وهو يأخذ True بحال أردنا أيقاف معامل التعلم عند نقطه بحيث لا يدخل الموديل في مرحلة overfit أي الضبط الزائد وfalse عكس ذلك البارمتر الخامس alpha يمثل معامل التنعيم حيث التنعيم هو طريقة لكي يتخلص الموديل من الضبط الزائد overfit ويلعب alpha دورا مهما في ذلك البارمتر السادس hidden_layer_sizes وهو يمثل عدد الطبقات ماعدا طبقة الدخل والخرج لأنهما لا تعتبرا طبقات مخفيه وعدد الخلايا في كل طبقه حيث الأرقام تدل على عدد الخلايا في الطبقه أما موقع الرقم يدل على الطبقه وعدد المواقع يدل على عدد الطبقات المخفيه فمثلا (10,200,30,4) يوجد أربعة طبقات لأنه يوجد أربع أرقام وكل رقم منها يدل على عدد الخلايا في طبقته مثلا الطبقة الأولى تحوي 10 خلايا طبعا قمت بشرح الشكل العام للموديل ولكن عن طريقة استخدامه سهل جدا فقط بعد أن تقوم بتقسيم الداتا إلى X_train, y_train,X_test, y_test تسطيع كتابة الأتي لعملية التدريب. MLPRegressorModel = MLPRegressor(activation='tanh', solver='adam', learning_rate='constant', early_stopping= False, alpha=0.0001 ,hidden_layer_sizes=(100, 3)) MLPRegressorModel.fit(X_train, y_train) حيث الدالة fit يوجد ضمنها جميع العمليات الداخلية لتدريب الشبكه العصبية يوجد دالة أخرى تستخدم لغرض التنبؤ كالاتي: y_pred = MLPRegressorModel.predict(X_test) حيث قمنا بالتنبؤ بالقيم المتوقعه لداتا الاختبار نستطيع أيضا حساب دقة الموديل أو كفاءته عن طريق التابع score ويكون وفق الشكل: print('MLPRegressorModel Test Score is : ' , MLPRegressorModel.score(X_test, y_test)) حيث قمنا بطباعة قيمتها لكي نرى كفاءة الموديل على بيانات الاختبار وهل هو يعاني من الضبط الزائد overfit أو الضبط الناقص underfit #استدعاء المكتبة from sklearn.neural_network import MLPRegressor #الشكل العام للموديل MLPRegressorModel = MLPRegressor(activation='tanh', solver='adam', learning_rate='constant', early_stopping= False, alpha=0.0001 ,hidden_layer_sizes=(100, 3)) #تدريب الموديل MLPRegressorModel.fit(X_train, y_train) #حساب الدقة على الاختبار print('MLPRegressorModel Test Score is : ' , MLPRegressorModel.score(X_test, y_test)) #حساب القيم المتوقعه y_pred = MLPRegressorModel.predict(X_test)1 نقطة
-
احاول مقارنة عددين من نوع Integer ودوما يعطيني false في جافا مع ان القيمتين يكونان متساويتين؟1 نقطة
-
من الصعب مساعدتك دون روئية أي جزء من الكود. ولكن بفرض أنه يتم استخدام == في عملية المقارنة، وهذا يعني أنه سيتم مقارنة في حال كان المتغيرين يدلان على نفس المكان في الذاكرة بدلاً من اختبار القيمة الحقيقية لكل متغيّر، وبالتالي ستعيد false. أما لاختبار قيم المتغيّرات من نوع integer يتم استخدام Integer.equals بدلاً من ==، مثال: if (firstNumber.equals(secondNumber){ System.out.println("true"); }else{ System.out.println("false"); }1 نقطة
-
ربما لأنك تستخدمين المعامل ==. وهو معامل نستخدمه مع ال primitive data types أي مع أنواع البيانات البدائية مثل int و float و double .. إلخ. لكنها لاتصلح للاستخدام مع البيانات من نوع object أي مع الكائنات لأنها في هذه الحالة ستقوم بمقارنة (المرجع) وليس القيمة التي يحملها. يجب استخدام التابع equal.مثلاً: import java.math.BigInteger; public class JavaApplication19 { public static void main(String[] args) { BigInteger x = new BigInteger("15"); // object متغير من النمط BigInteger y = new BigInteger("15"); // object متغير من النمط System.out.println(x.equals(y)); // true System.out.println(x==y); // false } }1 نقطة
-
يمكنك استخدام التابع sort الذي له الشكل التالي: list.sort(key = len,reverse=False) key و reverse وسيطان اختياريان. key يمثل تابع لتنفيذ الفرز على أساسه وفي حالتنا سنمرر له التابع len وبالتالي سيتم الفرز على أساس طول كل كلمة. في حال ضبط reverse على True سيكون الترتيب تنازلي. Hsoub = ['ali', 'ml', 'python'] Hsoub.sort(key = len,reverse=True) print(Hsoub) # output: ['python', 'ali', 'ml'] كما يمكنك استخدام هذا التابع لفرز العناصر داخل ال list مهما كان نوعها.1 نقطة
-
يمكن ترتيب عناصر قائمة بناءً على طول نص كل عنصر في هذه القائمة من خلال التابع sort كالتالي: >>> lst = ['sssss', 'ss', 'saa'] >>> lst.sort(key=len) >>> lst ['ss', 'saa', 'sssss'] >>> كما يمكن إستخدام نفس التابع لعكس ترتيب عناصر القائمة كالتالي: >>> lst.sort(key=len, reverse = True) >>> lst ['sssss', 'saa', 'ss'] >>>1 نقطة
-
حاولي أن تضعي هذا السطر في الكائن module.exports target: 'node', هذا هو الملف بعد التعديل webpack.config.js ثم قومي بتشغيل الأمر npm run build1 نقطة
-
1 نقطة
-
1 نقطة
-
مرحبًا هالة, يمكنك فعل ذلك عن طريق الاستعلام التالي SELECT MIN(column_name) as minimum FROM Persons ومن ثم باستخدام حلقة تكرار و عند الوصول للتكرار المرة الرابعة ممكن تطبعي النتيجة, أو من خلال استخدام Limit, offset SELECT MIN(column_name) as minimum FROM Persons LIMIT 1 OFFSET 4 SELECT MIN(column_name) as minimum FROM Persons LIMIT 1, 41 نقطة
-
1 نقطة
-
لدي مشروع لارافل على نظام التشغيل Ubuntu، وعند رفع الملفات من خلال المشروع يظهر لدي الخطأ التالي: GD Library extension not available with this PHP installation Ubuntu Nginx نظام التشغيل لدي: ubuntu 14.04، واستخدم Nginx كخادم للويب. وقمت بالتأكد من إعطاء الصلاحيات اللازمة 777 على المجلّد public/uploads. كيف أستطيع حل المشكلة؟1 نقطة
-
عندما أقوم بإجراء اختبار الوحدة على بعض التوابع في المشروع، يظهر لدي الخطأ التالي: There was 1 failure: 1) Warning No tests found in class "UsersTest". FAILURES! Tests: 2, Assertions: 1, Failures: أي لا يتم التعرف على أي اختبار داخل الصف. وهذا هو الصف المسؤول عن الاختبار: class UsersTest extends MainTest { public function fetching_users() { $this->times(5)->makeUser(); $this->getJson('api/users'); $this->assertResponseOk(); } private function createUser($userFields=[]) { $user = array_merge([ 'status' => $this->fake->sentence, 'bio' => $this->fake->paragragraph ], $userFields); while($this->times --)User::create($user); } } كيف يمكنني حل هذه المشكلة؟1 نقطة
-
يجب أخبار phpunit ان يتعامل مع الدالة كاختبار, بغض النظر عن اسم الدالة بهذا الشكل /** * @test */ public function add_some_thing(){ ///... } يمكنك مراجعة test@ من هنا . أو يمكنك بدء الدالة بكلمة test حتى تتعرف عليها phpunit بهذا الشكل public function test_add_some_thing(){ ///... }1 نقطة
-
هي أحد طرق تقسيم الداتا هي متل KFold ولكن تختلف عنها بأنها مجموعه من Kfold، ولكن بتنويعات أكبر، ويتم استخدامها في حالة كانت البيانات قليلة جداً وأردنا أن يكون تقييم النموذج دقيق جداً (أشار لذلك فرانسوا كوليت)، لننتقل إلى الكود البرمجي لسهولة الفهم في التطبيق #استدعاء المكتبات: import numpy as np from sklearn.model_selection import RepeatedKFold قمنا باستدعاء المكتبة numpy لتشكيل الداتا، واستدعاء الوظيفه RepeatedKFold من الوحدة model_selection في مكتبة sklearn #تشكيل الداتا الدخل والخرج: X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]]) y = np.array([11, 22, 33, 44]) حيث X مصفوفة أبعادها 4 أسطر وعمودين وy عمود واحد بأربع أسطر. #RepeatedKFold rkf = RepeatedKFold(n_splits=4, n_repeats=4) البارمتر الأول n_splits عدد صحيح لتحديد عدد الأجزاء folds وهي افتراضية في sklearn من 3 إلى 5. البارمتر الثاني n_repeats وهو نقطة الاختلاف عن KFolds هو عدد صحيح يمثل عدد KFolds. نفس الأمر في Kfolds مرور حلقة حيث يتم استخدام اثنين من الاندكسات في الحلقة للمرور على التدريب والاختبار وتحوي kf.split(X) هذه الاندكسات وهنا عدد المحاولات سوف يكون في مثالنا: n_splits*n_repeats=4*4=16 أي 4 Kfolds وكل kfold يحوي 4 تقسيمات مختلفه في كل مره. نقوم بطباعة الاندكس للتدريب والاختبار في كل محاوله وبعدها تخزين التدريب والاختبار ومن ثم طباعة كل منها: for train_index, test_index in rkf.split(X): print("TRAIN:", train_index, "TEST:", test_index) X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print('X_train \n' , X_train) print('X_test \n' , X_test) print('y_train \n' ,y_train) print('y_test \n' , y_test) print('*********************') الكود كامل: #استدعاء المكتبات import numpy as np from sklearn.model_selection import RepeatedKFold #تشكيل الداتاالدخل والخرج X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]]) y = np.array([11, 22, 33, 44]) #RepeatedKFold rkf = RepeatedKFold(n_splits=2, n_repeats=4, random_state=44) for train_index, test_index in rkf.split(X): print("TRAIN:", train_index, "TEST:", test_index) X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print('X_train \n' , X_train) print('X_test \n' , X_test) print('y_train \n' ,y_train) print('y_test \n' , y_test) print('*********************')1 نقطة
-
بالنسبة لتغير إتجاه عرض الموقع (من اليمين إلى اليسار أو من اليسار إلى اليمين) فيمكن عمل ذلك من خلال خاصية direction في CSS كالتالي: /* لتغير إتجاه كامل الموقع */ html { direction: rtl; /* Right To Left */ } /* كما يمكن تغير إتجاه عنصر معين فقط كالتالي*/ .post-container { direction: rtl; } عند إستخدام الخاصية السابقة قد تواجه الكثير من المشاكل والأخطاء في الموقع، وذلك بسبب خواص مثل margin و padding و float والتي يكون لها إتجاه معين (يمين أو يسار) وعند تغير إتجاه الموقع من خلال خاصية direction فإنك يجب أن تقوم بتغير قيمة هذه الخواص وغيرها من الخواص يدويًا وسيختلف هذا الأمر بالطبع من موقع إلى آخر، إن لم يكن لديك خبرة بالأمور البرمجة فيمكنك أن تقوم بتوظيف مستقل من أحد مواقع العمل الحر ليقوم بتغير إتجاه الموقع. أما بالنسبة إلى تغير لغة الموقع (من العربية إلى الإنجليزية على سبيل المثال)، فيجب أن تقوم بعمل الكثير من التغيرات أولها أن تقوم بتجميع كل نصوص الموقع في ملف json مثلًا أو في قاعدة بيانات، وتقوم بعمل مثل هذا الملف مرة أخرى بلغة مختلفة بشرط أن يتفق الملفان في المفاتيح، كالتالي: // en.json { "website title": "Website Name", "description": "a blog about technology" } // ar.json { "website title": "اسم الموقع", "description": "مدونة تتحدث حول التكنولوجيا" } يوجد العديد من المكتبات والحزم التي تقوم بعمل هذا الأمر ويختلف الأمر حسب التقنيات المستخدمة في إنشاء الموقع (ووردبريس، Laravel، Express.js)، ومن أمثلة هذه الحزم والمكتبات: react-i18next laravel-localization multilingual1 نقطة
-
هو أحد الطرق لتقسيم البيانات بدلا من استخدام train_test_split ويستخدم في حالة كانت البيانات قليلة. import numpy as np from sklearn.model_selection import KFold قمنا باستدعاء المكتبة numpy لتشكيل داتا مزيفه واستدعاء الوظيفه KFold من الوحدة model_selection في مكتبة sklearn #تكوين داتا مزيفة مكونة من أرقام عشوائية: X = np.random.random((1,15)).reshape((5, 3)) y = np.random.random((5,1)) في السطرين السابقين تم تشكيل X ,y كداتا مزيفه (أرقام عشوائيه )حيث X أبعادها 5 أسطر مع ثلاث أعمده وتحوي أرقام عشوائيه أما y عمود واحد بخمس أسطر وتحوي أرقام عشوائية #تقسيم الداتا المزيفه إلى أجزاء : لكن بداية سنعرض الصيغة العامة للتابع: sklearn.model_selection.KFold(n_splits=5, shuffle=False, random_state=None) الوظيفة KFold تأخذ البارمترات التالية: البارمتر الأول n_splits عدد صحيح لتحديد عدد الأجزاء folds وهي افتراضية في sklearn من 3 إلى 5. البارمتر الثاني shuffle متحول بولياني يأخذ True لكي يتم خلط الداتا قبل عملية التقسيم أي جعلها عشوائية ويأخذ False عندما لا نريد خلط الداتا. randomstate: للتحكم بعملية الخلط. وقد تحدثت عنه في هذا الرابط: الأن في مثالنا تم تقسيم الداتا إلى 5 أجزاء مع خلط الداتا قبل عملية التقسيم. وللوصول إلى كل جزء وما يحوية لديك الأسطر التالية حيث يتم استخدام اثنين من الاندكسات في الحلقة للمرور على التدريب والاختبار وتحوي kf.split(X) هذه الاندكسات لكل محاولة من المحاولات يقصد بالمحاولات اي عملية التقسيم المختلفة التي ذكرناها سابقاً بعد ذلك في كل مرور على الحلقة يتم طباعة الاندكس الخاص بالتدريب والاختبار وبعد ذلك تم تخزين بيانات التدريب والاختبار وبعدها طباعة الابعاد لكل منها في كل محاولة. # المثال: #استدعاء المكتبات import numpy as np from sklearn.model_selection import KFold #تكوين داتا مزيفة مكونة من أرقام عشوائية X = np.random.random((1,15)).reshape((5, 3)) y = np.random.random((5,1)) #تقسيم الداتا المزيفه إلى أجزاء kf = KFold(n_splits=2, random_state=44, shuffle =True) #KFold Data for train_index, test_index in kf.split(X): print('Train Data is : \n', train_index) print('Test Data is : \n', test_index) print('-------------------------------') X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print('X_train Shape is ' , X_train.shape) print('X_test Shape is ' , X_test.shape) print('y_train Shape is ' ,y_train.shape) print('y_test Shape is ' , y_test.shape) print('========================================')1 نقطة
-
هو معيار لقياس كفاءة نماذج التصنيف Classification. يعتمد على حساب عدد مرات اللاتطابق بين القيم الحقيقية والقيم المتوقعة. يمكن تطبيقه باستخدام مكتبة Sklearn كالتالي: sklearn.metrics.zero_one_loss(y_true, y_pred, normalize=True) الوسيط الأول والثاني يمثلان القيم الحقيقية والمتوقعة على التوالي. الوسيط الأخير في حال ضبطه على True سيعيد عدد مرات اللاتطابق كقيمة عشرية. في حال ضبطه على False يعيد عدد مرات اللاتطابق. المثال يوضح: from sklearn.metrics import zero_one_loss y_pred = [1, 0, 2, 1] y_true = [1, 0, 3, 1] z1=zero_one_loss(y_true, y_pred,normalize=True) print(z1) # 0.25 z2=zero_one_loss(y_true, y_pred, normalize=False) # print(z2) # 1 # Machine Learning is everywhere # Written by Ali Ahmed1 نقطة
-
يحاول الانحدار الخطي LinearRegression نمذجة العلاقة بين متغيرين X وY من خلال ملاءمة معادلة خطية (خط مستقيم) للبيانات التي يتم التدريب عليها وهو من الشكل Y=WX+b. ويستخدم في مهام التنبؤ Regression (مثل توقع أسعار المنازل مثلاُ أو توقع عدد الإصابات بمرض معين). ندعو X بال features و b بال bias (وهي تكافئ الإزاحة) بينما w تمثل أوزان النموذج (وهي تكافئ ميل المستقيم). نميز نوعين للتوقع الخطي: Univariate Linear Regression : أي التوقع الخطي الذي يعتمد فيه الخرج Y على One feature أي تكون X عبارة عن متغير واحد. Multiple linear regression : أي التوقع الخطي الذي يعتمد فيه الخرج Y على أكتر من feature أي تكون X عبارة عن x1,x2,...,xn. يمكن تطبيق التوقع الخطي عن طريق مكتبة Sklearn. يتم استخدامها عبر الموديول .linear_model.LinearRegression sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None) الوسطاء: fit_intercept: لجعل المستقيم يتقاطع مع أفضل نقطة على المحور العيني y. copy_X: وسيط بولياني، في حال ضبطه على True سوف يأخذ نسخة من البيانات ، وبالتالي لاتتأثر البيانات الأصلية بالتعديل، ويفيدنا في حالة قمنا بعمل Normalize للبيانات. normalize: وسيط بولياني، في حال ضبطه على True سوف يقوم بتوحيد البيانات (تقييسها) اعتماداً على المقياس L2norm. وقد سبق وتحدثت عن هذا الموضوع في هذا الرابط: n_jobs: لتحديد عدد العمليات التي ستتم بالتوازي (Threads) أي لزيادة سرعة التنفيذ، افتراضياُ تكون قيمته None أي بدون تسريع، وبالتالي لزيادة التسريع نضع عدد صحيح وكلما زاد العدد كلما زاد التسريع (التسريع يتناسب مع قدرات جهازك)، وفي حال كان لديك GPU وأردت التدريب عليها فقم بضبطه على -1. أهم ال attributes: _coef: الأوزان التي حصلنا عليها بعد انتهاء التدريب وهي مصفوفة بأبعاد (,عدد الfeatures). أهم التوابع: fit(data, truevalue): للقيام بعملية التدريب. predict(data): دالة التوقع ونمرر لها البيانات وتعطيك التوقع لها. score(data, truevalue): لمعرفة مدي كفاءة النموذج ونمرر لها بيانات الاختبار والقيم الحقيقية لها فيقوم بعمل predict للداتا الممررة ثم يقارنها بالقيم الحقيقية ويرد الناتج حسي معيار R Squaerd . إليك التطبيق العملي: الداتاسيت هي مواصفات منازلX مع أسعارها Y في مدينة بوسطن. from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression # تحميل الداتاسيت BostonData = load_boston() x = BostonData.data y = BostonData.target # تقسيم الداتا إلى عينة تدريب وعينة اختبار X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=33, shuffle =True) #تعريف LinearRegressionModel LR = LinearRegression(fit_intercept=True,copy_X=True,n_jobs=-1) LR.fit(X_train, y_train) print('Train Score is : ' ,LR.score(X_train, y_train)) # R Squaerd on trainset print('Test Score is : ' , LR.score(X_test, y_test)) # R Squaerd on testset print('Coef is : \n' , LR.coef_) # Coefficent # حساب القيم المتوقعة y_pred = LR.predict(X_test) print(y_pred[0:10]) # عرض القيم الحقيقية print(y_test[0:10]) # Machine Learning is everywhere1 نقطة
-
وفقاً للتوثيق الرسمي في لارافل، إن جميع القيم المشفرة في لارافل يتم تشفيرها من خلال مايعرف بـ MAC - message authentication code. ولذلك لا يمكن تغيير التشفير لقيمة تم تشفيرها مسبقاً من خلال مشروع آخر. أي بمعنى آخر، قد تحدث المشكلة نتيجة لتغيير المفتاح في المشروع، ويتم ذلك عادة عند نقل المشاريع أو نسخ الأكواد بين مشروع وآخر، وبالتالي يتغيّر App Key في مشروع لارافيل وعند التعامل مع البيانات المخزّنة مسبقاً في قاعدة البيانات والتي تم تشفيرها من خلال مشروع آخر تحدث هذه المشكلة لأنه لا يمكن لقيمة App key الجديدة من فك تشفير البيانات السابقة والتي تم حفظها بشكل مشفّر مسبقاً من خلال المفتاح السابق. مما قد يؤدي أيضاً في حالتك لتشفير بعض البيانات في القاعدة بمفتاح وبيانات أخرى بمفتاح آخر وهي التي في حالتك تظهر فيها هذه المشكلة عدى عن الأخرى. لذلك يجب التأكد من قيمة App Key عند نقل المشاريع التي يتم التعامل فيها مع نفس البيانات على خوادم قواعد البيانات. ومن إحدى المشاكل التي قد تطرأ أيضاً اختلاف أنماط تخزين كلمة المرور بين قاعدة بيانات وأخرى بين نسخ لارافل من النمط varchar(191) والتي بدورها لا تستطيع تخزين كامل القيمة المشفرة لكلمة المرور بل يتم تخزين جزء منها فقط. لذلك ينصح أيضاً عند التعامل مع مشاريع مختلفة أو نسخ مختلفة تحويل حقل كلمة المرور إلى النمط longtext أو text وخاصةً عندما تكون كلمات المرور غير محددة الطول.1 نقطة
-
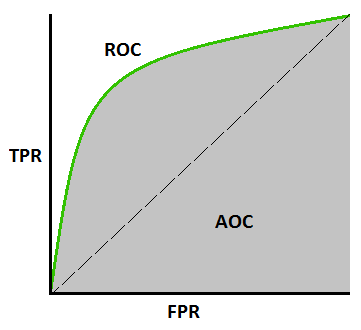
ROC&AUC Score ROC (Receiver Operating Characteristics)curve AUC (Area Under The Curve) ROC&AUC Score: هو معيار لقياس كفاءة نماذج التصنيف. للفهم جيداً يجب أن يكون لديك معرفة حول Recall(Sensitivity) و Precision(Specificity) وقد أشرت لهما سابقاً في هذا الرابط: https://academy.hsoub.com/questions/15466-حساب-ال-precision-و- recall-باستخدام-مكتبة-scikit-learn/ في الصورة المرفقة رسم بياني يعبر عن ROC&AUC ، بحيث : أولاً: <<TPR (True Positive Rate) or Recall or Sensitivity>> يمثل المحور العمودي، ويساوي إلى TP/(TP+FN) ويعبر عن ال Recall أي ال Sensitivity. ثانياً: <<FPR(False Positive Rate)>> ويساوي إلى FP/(FP+TN) أي أنه متمم ال Specificity أي : FPR=1-Specificity. ثالثاً: ROC: يمثل المنحنى الاحتمالي الذي يعبر عن العلاقة بين المحورين. رابعاً: AUC هو المساحة تحت المنحنى ويعبر عن درجة قدرة النموذج على الفصل بين الفئات Classes. ستلاحظ في الأكواد التالية أن زيادة المساحة تحت المنحني تشير إلى أداء أقوى للنموذج. مناقشة القيم أو قراءة القيم: كلما كانت درجة AUC أكبر كلما كان النموذج أفضل علماً أن أعلى قيمة لها 1 وأقل قيمة 0. في حال كانت قيمة AUC=1 فهذا يعني أن النموذج قادر على الفصل بين الClasses بنسبة 100%. الكود رقم 1 يعبر عن هذه الحالة. AUC=0.5 فهذا يعني أن النموذج غير قادر على الفصل بين ال Classes اطلاقاً وهي حالة سيئة، وفيه يكون النموذج غير قادر على إعطاء قرار، أي مثلا في مهمة تصنيف صور القطط والكلاب تشير قيمة 0.5 لل AUC إلى أن النموذج سيقف حائراً أمام أي صورة أي كأن يقول أن هذه الصورة هي 50% كلب و 50% قط. الكود رقم 2 يعبر عن هذه الحالة. AUC=0 فهذا يعني أن النموذج يتنبأ بشكل عكسي بالقيم أي يتموقع أن الأصناف الإيجابية سلبية والعكس بالعكس أي يقول عن القط كلب والكلب قط وبكل ثقة. الكود رقم 3 يعبر عن هذه الحالة. الشكل العام للتابع الذي يقوم بحساب ROC في Sklearn: sklearn.metrics.roc_curve(y_true, y_score) الوسيطين الأول والثاني يعبران عن القيم الحقيقية والمتوقعة على التوالي. يرد التابع 3 قيم fpr و tpr والعتبة وسنستخدم هذه القيم لحساب درجة AUC. الشكل العام للتابع الذي يقوم بحساب AUC في Sklearn: sklearn.metrics.auc(fpr, tpr) قم بتجريب الأكواد التالية لتحصل على الخرج وترى الفروقات: # الكود 1 ############################# Case 1 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([1 , 1 , 0 , 1, 1]) y_pred = np.array([0.99 ,0.02 ,0.01, 0.99,0.999]) #لاحظ نسبة التطابق fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) # طباعة قيم الخرج # لرسم المنحنى plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) # حساب قيمة AUC print('AUC Value : ', AUC) # طباعة القيمة #الكود 2 ############################# Case 2 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([0 ,1 ,0 ,1,0]) y_pred = np.array([0.5 ,0.5 ,0.5, 0.5, 0.5]) # لاحظ أننا غيرنا القيم fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) print('AUC Value : ', AUC) # الكود 3 ############################# Case 3 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([0 ,1 ,0 ,0,0]) y_pred = np.array([0.9 ,0.1 ,0.9, 0.9, 0.9]) fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) print('AUC Value : ', AUC)1 نقطة
-
هما معياران لقياس كفاءة نماذج التصنيف Classifications. أولاً: Precision هو نسبة (المتوقع) الإيجابي الصحيح على نسبة (((المتوقع))) الإيجابي الكلي ويعبر عنه بالعلاقة التالية: Precision = TP/(TP+FP) لاحظ أن البسط يعبر عن كل العينات التي قال عنها نموذجنا أنها P وهي بالغعل P. لاحظ أن المقام (TP+FP) يشير إلى كل العينات التي اعتبرها نموذجنا P سواءاً أكان التوقع صحيح أم لا. ويمكن أن نعبر عنه بالصيغة؟ كم هي عدد العينات التي توقع النموذج أنها + وكانت بالفعل + من بين كل التوقعات التي توقع أنها +. لتطبيقه باستخددام scikit-learn نستخدم الصيغة التالية: sklearn.metrics.precision_score(y_true, y_pred) مثال: from sklearn.metrics import precision_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج precision=precision_score(y_true, y_pred) # لطباعة الناتج كنسبة مئوية print(str(precision*100)+'%',sep='') ثانياً: Recall هي كل (التوقعات) الإيجابية الصحيحة مقسومة على العدد الكلي للحالات الإيجابية. Recall = TP/(TP+FN) البسط لم يتغير. المقام تم استبدال FP ب FN ليصبح (TP+FN) ويشير إلى عدد العينات الإيجابية كلها التي اكتشفها النموذج والتي لم يكتشفها أصلاً. sklearn.metrics.recall_score(y_true, y_pred) مثال: from sklearn.metrics import recall_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج recall=recall_score(y_true, y_pred) # لطباعة الناتج كنسبة مئوية print(str(recall*100)+'%',sep='') # 75.0% # للتنويه: الرابط التالي يحوي شرح لمفاهيم TPو TN والبقية:1 نقطة
-
يعتبر من أهم معايير قياس دقة نماذج التصنيف Classification. وهو نسبة ماتوقعناه بشكل صحيح إلى مجموع التوقعات الكلية ويستخدم بكثرة، ويمكن التعبير عنه بالصيغة التالية: Accuracy = (TP+TN)/(TP+FP+FN+TN) الصيغة العامة للتابع الذي يقوم بحساب الدقة في مكتبة scikit-learn: sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True) حيث أن أول وثاني وسيط يمثلان القيم الحقيقية والمتوقعة على التوالي. الوسيط normalize في حال تم ضبطه على true يعيد قيمة عشرية تمثل الدقة (الحالة الافتراضية)، وفي حال ضبطه على False سيقوم بحساب TP+TN أي عدد التوقعات الصحيحة للنموذج. مثال: from sklearn.metrics import accuracy_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج print(accuracy_score(y_true, y_pred, normalize=True)) # 0.8333333333333334 # لطباعة الناتج كنسبة مئوية print(accuracy_score(y_true, y_pred)*100,'%',sep='') # 83.33333333333334% # تنويه: تجد شرح المفاهيم TP,TN,FP,FN في الرابط التالي بالتفصيل.1 نقطة
-
يتم ذلك باستخدام التابع التالي: sklearn.model_selection.train_test_split(data,label, test_size=None, train_size=None, random_state=None, shuffle=True) يقوم التابع train_test_split بتقسيم البيانات إلى عينات تدريب وعينات اختبار. data: تمثل مجموعة البيانات. label: تمثل الفئات (classes). test_size: لتحديد النسبة المئوية التي سيتم اقتطاعها من البيانات لاستخدامها كعينة اختبار. لو وضعنا 0.2، سيتم تخصيص 20% من البيانات للاستخدام كعينة اختبار. train_size: لتحديد النسبة المئوية التي سيتم اقتطاعها من البيانات لاستخدامها كعينة تدريب. random_state: هذا الوسيط غامض لدى الكثيرين. إنه يتحكم بطريقة الخلط المطبقة على البيانات أي لتحديد نظام العشوائية ويأخذ قيمة من النمط integer ويمكنك وضع أي قيمة تريدها، هذا الرقم يفهمه المترجم بطريقة معينة على أنه نمط معين للتقسيم. لنفهم فائدة هذا الوسيط سأعطيك المثال التالي: لنفرض أننا نعمل في فريق على مهمة تعلم آلة معينة. في حال لم نستخدم random_state سوف يتم تقسيم البيانات على جهاز كل عضو من الفريق بطريقة مختلفة، أما إذا اخترنا جميعاً قيمة ثابتة ولتكن 44 فهذا يعني أن البيانات ستقسم بنفس الطريقة على جهاز كل عضو، ولو أعدنا التقسيم 1000 مرة سيكون نفسه. وطريقة قسم البيانات مهمة فمثلاً إذا كانت عناصر مجموعة الاختبار a تختلف عن عناصر مجموعة الاختبار b، هذا سيؤدي إلى اختلاف ال score بين المجموعتين. shuffle: لعمل خلط للبيانات قبل تقسيمها (أي بعثرة أو إعادة ترتيب العينات بشكل عشوائي). في حال وضعنا False لن تتم البعثرة (يفضل وضعها True دوماً). الكود التالي يوضح العملية: # سنقوم بتحميل الداتاسيت الخاصة بأسعار المنازل في مدينة يوسطن ونقوم بتقسيمها import numpy as np from sklearn.model_selection import train_test_split from sklearn.datasets import load_boston # تحميل الداتاسيت BostonData = load_boston() data = BostonData.data label = BostonData.target # عرض حجم الداتا print('The shape of data:',data.shape,'\n') # The shape of data: (506, 13) أي لدينا 506 عينات # تقسيم الداتا X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.2, random_state=44, shuffle =True) # لاحظ أننا حددنا 20 بالمئة كعينة اختبار وبالتالي سيتم اعتبار الباقي عينة تدريب تلقائياً # عرض حجم البيانات بعد التقسيم print('The shape of X_train:',X_train.shape) # The shape of X_train: (354, 13) print('The shape of X_test:',X_test.shape) # The shape of X_test: (152, 13) print('The shape of y_train:',y_train.shape) # The shape of y_train: (354,) print('The shape of y_test:',y_test.shape) # The shape of y_test: (152,)1 نقطة
-
error matrix أو confusion_matrix: هي مصفوفة تستخدم لتقييم أداء نماذج التصنيف، أي نستخدمها عندما تكون المهمة هي مهمة تصنيف Classification. هذه المصفوفة تقوم بحساب TP و FP و FN و TN وترد مصفوفة تعبر عنهم بأبعاد (n_classes, n_classes). سأعطي مثال لشرحهم: تجري إحدى الكليات فحصاً لمرض كورونا باستخدام التعلم الآلي على جميع طلابها. الناتج إما مصاب بكورونا + أو سليم -. وبالتالي سيكون هناك 4 حالات من أجل طالب x. إذا كانت تبدأ بـ True، فإن التنبؤ كان صحيحاً سواء كان مصاباً بمرض كورونا أم لا. إذا كانت تبدأ بـ False، فإن التنبؤ كان غير صحيح. P تدل على الفئة الإيجابية و N السلبية، وهما خرج برنامجنا. True positive (TP): النموذج يتوقع أن الطالب x حالته + والطالب x هو فعلاً مصاب (وهذا جيد). أي توقع أن الشخص مصاب وهو مصاب فعلاً. True negative (TN): النموذج يتوقع أن الطالب x حالته - والطالب سليم (وهذا جيد). أي شخص سليم و تنبأ أنه سليم بشكل صحيح. False positive (FP): النموذج يتوقع أن الطالب x حالته + والطالب غير مصاب (وهذا سيئ). أي شخص سليم وتوقع أنه مصاب. False negative (FN): النموذج يتوقع أن الطالب x حالته - والطالب مصاب (وهذا الأسوأ). أي شخص مصاب وتوقع أنه سليم. لتطبيقها باستخدام مكتبة Sklearn نستدعي التابع confusion_matrix من الموديول metrics والمثال التالي يبين كل شيء: sklearn.metrics.confusion_matrix(y_true, y_pred, normalize=None) أول وسيطين يمثلان القيم الحقيقية والقيم المتوقعة، على التوالي. أما الوسيط الأخير فهو اختياري ويستعمل لعمل normalize للقيم وهو يأخذ 3 قيم: all: بالتالي يقسم كل قيم المصفوفة على مجموع كل التوقعات (جرب بنفسك). true: يقسم كل القيم في عمود j على مجموع القيم فيه. pred: يقسم كل القيم في سطر i على مجموع القيم فيه. لاستخراج قيم tp و tn و fp و fn من المصفوفة نستخدم التابع ()ravel مع ملاحظة أنه لايمكنك استخدام هذا التابع إلى في حالة أن التصنيف ثنائي. from sklearn.metrics import confusion_matrix y_true = ["cat", "dog", "cat", "cat", "dog", "dog","cat","cat"] y_pred = ["dog", "dog", "cat", "cat", "dog", "cat","cat","cat"] # حساب المصفوفة cm=confusion_matrix(y_true, y_pred,normalize=None') # عرض نتيجة المصفوفة print(cm) # لاستخراج القيم tp,fp,fn,tn=cm.ravel() #يمكنك التعبير عن هذه القيم بالرسم import matplotlib.pyplot as plt import seaborn as sea sea.heatmap(cm, center = True) plt.show()1 نقطة
-
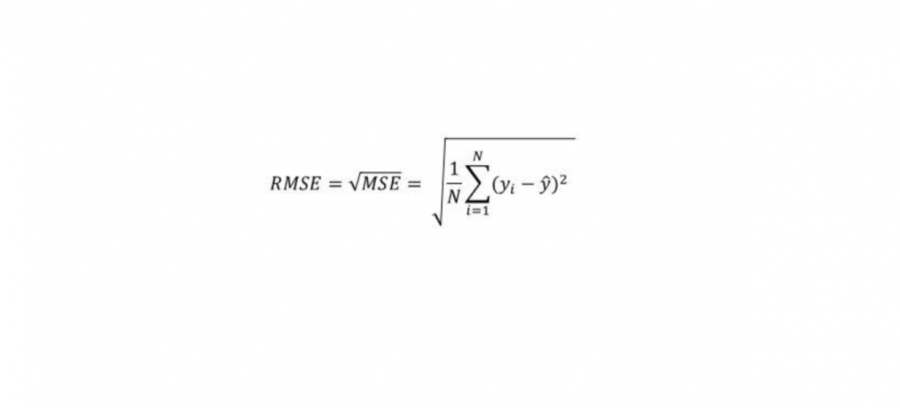
بشكل عام هناك 4 مقاييس أساسية لقياس كفاءة المودل عندما تكون المهمة من نوع Regrission (توقع): أول ورابع معيار هم الأكثر استخداماً. أولاً: Mean Absolute Error وهي متوسط الفروق بالقيمة المطلقة بين القيم الحقيقية والقيم المتوقعة في مجموعة البيانات، والصورة المرفقة في الأسفل توضح الشكل العام للمعادلة الرياضية المعبرة عنها. ثانياً: Mean Squared Error وهي متوسط مربع الفروق بين القيم الحقيقية والمتوقعة، في الأسفل تم توضيح الشكل الرياضي للمعادلة. ثالثاُ: Root Mean Squared Error وهو جذر ال Mean Squared Error، في الأسفل تم توضيح الشكل الرياضي للمعادلة. رابعاً: R Squared معايير القياس المذكورة أعلاه سيكون لها قيم مختلفة لنماذج مختلفة، أي ليس لها مجال ثابت لكي نخمن على أساسه هل النموذج جيد أم لا، فمثلاً في مشكلة توقع أسعار المنازل قد يكون مجال القيم لهما بين 100 و 400 دولار وفي مسألة توقع درجة الحرارة قد يكون المجال بين ال 1 و 4 (أي القيم الناتجة ليست سهلة القراءة)، أما في هذا المقياس فسوف يكون مجال القيم محصور بين ال 0 وال 1، بحيث 1 تعني أن النموذج خالي من الأخطاء و 0 تعني أن النموذج فاشل تماماً. في الصورة المرفقة في الأسفل تم توضيح الشكل الرياضي للمعادلة. مثال: # انتبه أن التابع mean_squared_error يقبل وسيط بولياني يسمى squared في حال ضبطه على True سيتم حساب MSE أما في حال ضبطه على False سوف يحسي MSE ثم يأخذ الجذر أي يصبح RMSE. ####################################### Example ############################################### # استيراد الدوال from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error from sklearn.metrics import r2_score y_true = [80.3, 100, -7.7] # نفرض أن القيم الحقيقية كانت y_pred = [85, 99, -0.5] # والقيم المتوقعة ####################################### MAE ################################################## print("MAE is: "+str(mean_absolute_error(y_true, y_pred))) # output: MAE is: 4.300000000000001 ####################################### MSE ################################################## print("MSE is:"+str(mean_squared_error(y_true, y_pred,squared=True))) # MSE is:24.976666666666677 ####################################### RMSE ################################################## print("RMSE is:"+str(mean_squared_error(y_true, y_pred,squared=False))) # RMSE is:4.997666121968001 ####################################### R Squaerd ################################################## print("R Squaerd is:"+str(r2_score(y_true, y_pred)))#R Squaerd is:0.9886074871600465 مثال واقعي على مهمة توقع أسعار المنازل في مدينة بوسطن، حيث أن البيانات تمثل مواصفات المنازل وأسعارها في تلك المدينة : ####################################### مثال عملي ################################################## from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error from sklearn.metrics import r2_score from sklearn.linear_model import LinearRegression # تحميل الداتاسيت BostonData = load_boston() x = BostonData.data y = BostonData.target # تقسيم الداتا إلى عينة تدريب وعينة اختبار X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=44, shuffle =True) #تعريف LinearRegressionModel LR = LinearRegression() LR.fit(X_train, y_train) # حساب القيم المتوقعة y_pred = LR.predict(X_test) # Mean Absolute Error MAE = mean_absolute_error(y_test, y_pred) print('Mean Absolute Error Value is : ', MAE) #Mean Absolute Error Value is : 3.4318693222761523 # Mean Squared Error MSE = mean_squared_error(y_test, y_pred,squared=True) print('Mean Squared Error Value is : ', MSE) #Mean Squared Error Value is : 21.439149523649792 # Root Mean Squared Error RMSE = mean_squared_error(y_test, y_pred,squared=False) print('Root Mean Squared Error Value is : ', RMSE) #Root Mean Squared Error Value is : 4.6302429227471205 # R Squaerd print("R Squaerd is: "+str(r2_score(y_test, y_pred))) # R Squaerd is: 0.7532417995961468 فرانسوا كوليت ينصح باعتماد MAE.1 نقطة