خاصية الطول Length للأشعة الهندسية في التصاميم ثلاثية الأبعاد

يناقش هذا المقال طول Length الأشعة وكيفية حساب هذا الطول باستخدام تمثيل المصفوفة العمودية للأشعة، وسنناقش في المقال التالي خاصيةً أخرى للأشعة، وهي خاصية الاتجاه Direction؛ إذ للأشعة بجميع أبعادها خاصيتان هما: الطول والاتجاه، ولكن سنستخدم أشعة في فضاء ثنائي الأبعاد للسهولة.

سنوضّح في هذا المقال المواضيع التالية:

طول الأشعة ثنائية وثلاثية الأبعاد.
صيغة فيثاغورس.
حساب طول الشعاع من خلال تمثيله بالمصفوفة العمودية.
طول الشعاع الصفري.
طول الشعاع السالب.

الأشعة المحاذية للمحورين X-Y

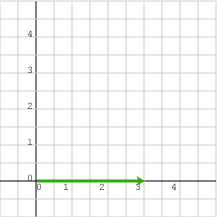
ما هو طول الشعاع التالي الذي تمثله المصفوفة العمودية ‎(3, 0)^T‎؟

يمكن القول أن الطول يساوي 3 وحدات.

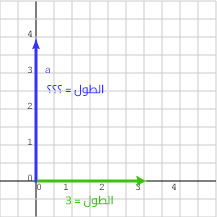
إذا كان هناك شعاع ثنائي الأبعاد يحاذي المحور x، فإن المصفوفة العمودية التي تمثله لها قيمة غير صفرية في العنصر الأول، وصفر في العنصر الثاني، إذ من السهل تحديد طول الشعاع الأخضر المُمثَّل بالمصفوفة العمودية ‎ (3, 0)^T‎في المخطط البياني التالي، فالطول هو قيمة العنصر الوحيد غير الصفري في تلك المصفوفة.

يحاذي الشعاع a (الشعاع الأزرق في المخطط البياني السابق) المحور y، ومصفوفته هي ‎(0, 4)^T‎، فما هو طول الشعاع a؟ طوله 4 وحدات، إذ يمكن قراءته من المخطط البياني، ولكن ليس للشعاع موقع ثابت طبعًا، لذلك يمكن رسم الشعاع a في أيّ مكان وسيكون له الطول نفسه.

صيغة فيثاغورس

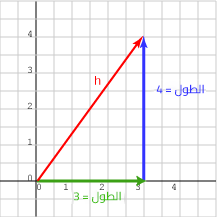
يوضح المخطط البياني التالي شعاعين بطول 3 و4 مع الشعاع الجديد h:

من الصعب معرفة طول الشعاع h، ولكنه ليس صعبًا كثيرًا؛ خاصةً إذا كنت على معرفة بقاعدة "3، 4، 5 في المثلثات قائمة الزاوية"، إذ يمكن ترتيب الأشعة الثلاثة في مثلث قائم الزاوية، بحيث يكون h هو الوتر، والضلعان الآخران هما 3 و 4؛ وبالتالي فإن طول h يساوي 5 باستخدام صيغة فيثاغورس والتي هي:

(طول الوتر)² = (طول الضلع القائمة الأولى)² + (طول الضلع القائمة الثانية)²

إذا استخدمنا صيغة فيثاغورس مع مثلث قائم الزاوية له ضلعان قائمان طولهما 3 و 4، فسنحصل على طول الوتر كما يلي:

‫(طول الوتر)² ‫= ‫3² + ‪‫4² ‫

‫(طول الوتر)² ‫=‫ ‪‫9 +‫ 16 = 25

(طول الوتر) = 5

إذًا ما هو طول الوتر في المثلث القائم الزاوية الذي طول ضلعيه 6 و 8؟ وما طول الوتر في المثلث القائم الزاوية الذي طول ضلعيه القائمين 6 و 8؟ سنستخدم للحل صيغة فيثاغورس كما يلي:

‫الطول² ‫= ‪ ‫6² + ‪‫6² ‫

‫الطول² ‫= ‪‫36 +‫ 64 = 100

الطول = 10

استخدام صيغة فيثاغورس لحساب طول الأشعة

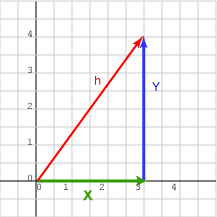
يمكن استخدام صيغة فيثاغورس لحساب طول الشعاع ثنائي الأبعاد. لنفترض أن الشعاع تمثّله المصفوفة العمودية ‎(x, y)^T‎، لذا ضع ذيل الشعاع عند نقطة الأصل، ثم أنشئ مثلثًا من خلال رسم الضلعين الآخرين كما في المخطط البياني السابق:

side_1 = (x, 0)^T

side_2 = (0, y)^T

طول الضلع الأول side_1 هو x، وطول الضلع الثاني side_2 هو y، وبالتالي ينتج لدينا أن الطول:

length (x, y)^T = √( x^T + y^T )

يمثّل الرمز √ الجذرَ التربيعي الموجب في هذه الصيغة، إذ لا نريد بالطبع أن يكون الطول سالبًا.

ما طول الشعاع الذي تمثله المصفوفة العمودية ‎(4, 3)^T‎؟ الطول يساوي 5.0، إذ يمكنك استخدام الصيغة السابقة، أو إدراك أنه مثلث قائم زاوية آخر أطول أضلاعه 3-4-5.

الرمز المستخدم لطول الشعاع

تعمل صيغة فيثاغورس مع الأشعة المحاذية للمحاور كما يلي:

length of( (8,0)^T ) = √( 8*8 + 0*0 ) = 8

لا يُعَد الاستمرار في قول "طول ( ) أو length of ( )‎" مناسبًا، لذا يوجد رمزٌ لذلك وهو:

طول ‎| a | = ( a )‎

للرمز a شريطٌ عمودي من كل جانب، وتستخدم الكتب أحيانًا شريطين عموديين على كل جانب، وبالتالي تكون الصيغة كما يلي:

‪| (x, y)^T | = √( x² + y² )

إذا كان ‎g = (1, 1)^T‎، فما هو | g | ؟

نعوّض في الصيغة كما يلي:

‪| g | = √( 1² + 1² )

‪= √2.0

‪= 1.414213562373

لاحظ أن الطول ليس 1.0 ولا 2.0، وهذا خطأ يقع فيه بعض الأشخاص.

إثبات متراجحة المثلث

تذكّر أن طول مجموع شعاعين أقل من أو يساوي مجموع طولي هذين الشعاعين:

طول ( v + u ) <= طول ( u ) + طول ( v )

وفي الصيغة الجديدة:

| u + v | <= | u | + | v |

لتكن لدينا الأشعة المُمثَّلة بالمصفوفات العمودية التالية:

u = (3, 4)^T

v = (3, -4)^T

w = u + v = (6, 0)^T

يوضّح المخطط البياني التالي كيفية عمل متراجحة المثلث في هذا المثال، إذ يكون مجموع طولي الشعاعين الأحمر والأزرق أقل من طول الشعاع الأخضر. ولكن هل يمكن تطبيق ذلك عدديًا؟ وما هي قيمة كلٍّ من | u | و | v | و | w |؟

إجابة:

‎u = (3, 4)^T‎ وبالتالي: ‎| u | = 5
‎v = (3, -4)^T‎ وبالتالي: ‎| v | = 5
‎w = u + v = (6, 0)^T‎ وبالتالي: ‎| w | = 6
طبعًا 6 < 5 + 5 مما يدل على أن: | u + v | <= | u | + | v |

تدريب عملي

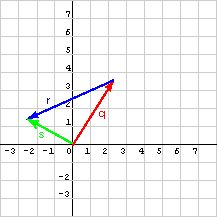
لا تكون عناصر الشعاع عادةً قيمًا صحيحةً بسيطة، ولتكن لدينا مثلًا بعض الأشعة المُمثَّلة بمصفوفات عمودية تحتوي على كسور عشرية في عناصرها كما يلي:

q = (2.2, 3.6)^T

r = (-4.8, -2.2)^T

s = q + r

يمكن طبعًا استخدام صيغة فيثاغورس، ولكنك ستحتاج إلى آلة حاسبة لاستخدامها.

‪| (x, y)^T | = √( x² + y² )

ما هي أطوال الأشعة q و r و s؟

‪| q | = √( 2.22.2 + 3.63.6 ) = √( 4.84 + 12.96 ) = √ 17.8 = 4.219

‪| r | = √( -4.8* -4.8 + -2.2 * -2.2 ) = √( 23.04 + 4.84 ) = √ 27.88 = 5.280

‪| s | = √( -2.6 * -2.6 + 1.4*1.4 ) = √( 6.76 + 1.96 ) = √ 8.72 = 2.953

يكون | s | أصغر من | q | + | r | كما هو متوقع.

حساب طول الأشعة ثلاثية الأبعاد

تكون للأشعة ثلاثية الأبعاد خاصية الطول، ويمكن استخدام الصيغة فيثاغورس نفسها لحساب الطول، إذ يكون طول الشعاع الذي تمثله مصفوفة مكونة من ثلاثة مكونات هو:

‪| (x, y, z)^T | = √( x² + y² + z²)

كما في المثال التالي:

‪| (1, 2, 3)^T | = √( 1² + 2² + 3² ) = √( 1 + 4 + 9 ) = √14 = 3.742

إذًا لنحسب طول ‎(2, -4, 4)^T‎ و ‎(-1, -2, 3)^T‎ كما يلي:

‪| (2, -4, 4)^T | = √( 2 * 2 + -4 * -4 + 4 * 4) = √( 4+ 16 + 16 ) = √36 = 6

‪| (-1, -2, 3)^T | = √( -1 * -1 + -2 * -2 + 3 * 3) = √( 1 + 4 + 9 ) = √14 = 3.742

يعطي تربيع عناصر الشعاع ناتج جمع للقيم الموجبة (أو الصفرية)، مما يضمن أن يكون الطول قيمة موجبة (أو صفرًا).

الأشعة الهندسية

ضع في بالك أن الأشعة هي كائنات هندسية، أي يُعبَّر عنها بطولٍ واتجاه في الفضاء.

تُمثَّل الأشعة بالمصفوفات العمودية، وتفترض صيغ حساب الطول في هذا المقال استخدام إطار إحداثي وأن الأشعة مُمثَّلة بمصفوفات عمودية ضمن هذا الإطار.

يمكن أن يناقش أيّ كتابٍ خاص بالرسوميات الحاسوبية كيفية استخدام الإحداثيات المتجانسة Homogeneous Coordinates لتمثيل الأشعة، إذ تستخدم هذه الطريقة مصفوفات عمودية مكونة من 4 مكونات لتمثيل الأشعة في فضاء ثلاثي الأبعاد، ويتطلب حساب طول الشعاع المُمثَّل بهذه الطريقة تعديل الصيغ، مع تجاهل المكون الرابع للمصفوفة العمودية.

لا تقلق بشأن هذه الطريقة حاليًا، إذ سنوضّح التفاصيل لاحقًا، وخذ الوقت الكافي لفهم فكرة أن المصفوفات العمودية التي نستخدمها ليست الطريقة الوحيدة لتمثيل الأشعة، وأن خاصية الطول هي خاصة بالشعاع، وليست خاصة بالمصفوفة العمودية التي تمثل هذا الشعاع، لذا قد تتساءل عن وجود أيّ أهمية لتمييز شيء ما عن تمثيله في علوم الحاسوب! حسنًا، نعم هناك أهمية طبعًا، ويُعَد ذلك من أهم الأفكار في علوم الحاسوب.

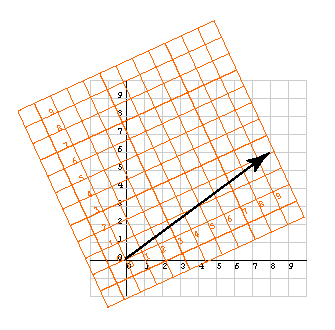
ليكن لدينًا مثلًا المخطط البياني التالي الذي يحتوي شعاعًا وإطارين للإحداثيات هما: إطار رمادي فاتح وإطار برتقالي.

نمثّل الشعاع بالمصفوفة العمودية ‎(8, 6)^T‎ في الإطار الرمادي الفاتح، ونمثّله في الإطار البرتقالي بالمصفوفة العمودية ‎(9.8, 2)^T‎، ولنفترض أن المحاور في كلا الإطارين مُدرَّجة باستخدام الوحدات نفسها (سم مثلًا).

يكون طول الشعاع باستخدام التمثيل الأول هو:

‪√( 8² + 6² ) = √( 64 + 36 )= √( 100 )= 10.0

ويكون طول الشعاع باستخدام التمثيل الثاني هو:

‪√( 9.8² + 2² ) = √( 96 + 4 ) = √( 100 ) = 10.0

ولكن هل ستنجح العملية الحسابية إذا وضعنا ذيل الشعاع في مكان آخر من الإطار؟ نعم، فليس للشعاع موضع محدّد، لذلك يمكن وضع الذيل في أيّ مكان تريده.

الطول قيمة موجبة أو صفرية

بما أن مربع الطول يساوي مجموع المربعات، وينتج عن تربيع الأعداد الحقيقية قيمة صفرية أو موجبة، فهذا يعني أنه يجب أن يكون الطول دائمًا صفرًا أو عددًا موجبًا.

‪| a | = | (a₁, a₂, a₃ )^T | = √( a₁² + a₂² + a₃² ) >= 0

يكون طول الشعاع ثلاثي الأبعاد صفرًا فقط عندما يكون هذا الشعاع هو الشعاع الصفري، إذ يُمثَّل الشعاع الصفري ثلاثي الأبعاد في جميع الإطارات الإحداثية كما يلي:

‪0 = (0, 0, 0)^T

ويكون طول الشعاع الصفري هو:

‪| 0 | = √( 0² + 0² + 0² ) = 0

يكون طول الشعاع الصفري ثنائي الأبعاد صفرًا أيضًا، وهو الشعاع ثنائي الأبعاد الوحيد الذي يكون طوله صفرًا. إذًا هل سيكون للشعاعين المتساويين الطول نفسه، وهل سيكون الشعاعان اللذان لهما الطول نفسه متساويين دائمًا؟

سيكون للشعاعين المتساويين الطول نفسه، إذ يجب أن تكون عناصرهما المتقابلة متساويةً، لذا يجب أن تكون عمليات التربيع المتقابلة متساوية أيضًا، وبالتالي يجب أن يكون المجموع متساويًا، ويجب أن يكون الطول متساويًا.
لن يكون الشعاعان اللذان لهما الطول نفسه متساويين دائمًا، إذ يمكن أن يكون مجموع مربعات العناصر متساويًا دون أن تكون العناصر نفسها متساوية.

طول الشعاع السالب

إذا كان v شعاعًا، فإن ‎-v هو شعاع يؤشّر إلى الاتجاه المعاكس، وإذا كان تمثيل v هو ‎(a, b, c)^T‎، فسيكون تمثيل ‎-v هو ‎(-a, -b, -c)^T‎، فما هي العلاقة بين طول الشعاعين v وطول ‎-v؟

العلاقة هي:

‪| v | = |-v|