الأشعة كيفية جمع الأشعة الهندسية للتصاميم ثلاثية الأبعاد

تعرّفنا في المقال السابق على جمع المصفوفات العمودية الذي يُعَد إجراءً سهلًا، وسنوضّح في هذا المقال سبب كون هذا الإجراء مفيدًا من خلال مناقشة كيفية تمثيله لعملية جمع الأشعة.

سنتعرّف في هذا المقال على المواضيع التالية:

• جمع الأشعة.
• جمع الأشعة باستخدام قاعدة الرأس إلى الذيل Head to Tail.
• قاعدة الرأس إلى الذيل في فضاء ثلاثي الأبعاد.
• الخاصية التجميعية Associative لجمع الأشعة.
• الخاصية التبديلية Commutative لجمع الأشعة.
• الإطارات الإحداثية Coordinate Frames.
• تمثيل النقاط الهندسية باستخدام إطارات الإحداثيات والمصفوفات العمودية.
• تمثيل الأشعة باستخدام المصفوفات العمودية.
• جمع الأشعة باستخدام المصفوفات العمودية.
• استخدام متوازي الأضلاع في عملية جمع الأشعة.
• متراجحة المثلث Triangle Inequality.
• الأشعة المرتبطة الخطية Collinear.
• جمع الأشعة الصفرية.
• عملية جمع شعاع ونقطة.

تذكير: اجمع المصفوفتين العموديتين التاليتين:

a = ( 3, 2 )^T

b = (-2, 1 )^T

والجواب هو:

a + b = ( 1, 3 )^T

الأشعة في الفضاء ثنائي الأبعاد

تُعَد الأشعة كائنات هندسية يمكن تمثيلها بطرق متعددة، ولكن يجب أن نفهم الفرق بين الكائن الهندسي (مثل النقطة أو الشعاع)، وطريقة تمثيله (باستخدام مصفوفة عمودية غالبًا).

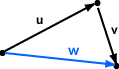
يوضّح المخطط البياني السابق النقاط A و B و C في فضاء ثنائي الأبعاد؛ حيث يُعبَّر عن الإزاحة Displacement بمسافة واتجاه، فالشعاع u هو الإزاحة من النقطة A إلى النقطة B، أما الشعاع v فهو الإزاحة من النقطة B إلى النقطة C. بينما يعبٌر الشعاع w عن الإزاحة من النقطة A إلى النقطة C؛ ويكون تأثير التحرك عبر الإزاحة u ثم عبر الإزاحة v هو تأثير التحرك عبر الإزاحة w نفسه وبالتالي يمكن القول أن:

u + v = w

عدم اعتمادية عملية جمع الأشعة على موضعها

هل تعتمد عملية جمع الأشعة على مكان وجودها؟ لا، فليس للأشعة موضع محدّد.

توضّح النقاط في المخطط البياني السابق كيفية حساب التأثير المشترك لإزاحتين من خلال جمعهما، ولكن لم يتضمّن جمعُ الإزاحات النقاط فعليًا، حيث يظهر جمع الأشعة عادةً كما في المخطط البياني السابق، الذي يوضح أن تأثير التحرك عبر الإزاحة u ثم التحرك عبر الإزاحة v هو تأثير التحرك عبر الإزاحة w نفسه.

لنفترض مثلًا أنك ترغب في نقل جميع نقاط كائن هندسي عبر الإزاحة u، ثم عبر الإزاحة v. يمكنك تطبيق ذلك من خلال تحريك كل نقطة عبر الإزاحة w.

قاعدة الرأس إلى الذيل Head-to-Tail

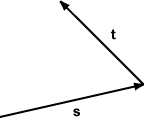
جرب رسم الخط الذي يمثل مجموع الشعاعين s و t:

والحل باستخدام قاعدة الرأس إلى الذيل هو:

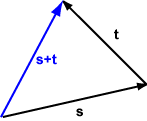
يمكن جمع الشعاعين v و u في المخطط البياني التالي من خلال تحريك الشعاع v مع الحفاظ على طوله ومنحاه Orientation حتى يلمس ذيلُ هذا الشعاع رأسَ الشعاع u، والناتج هو الشعاع المتشكّل من ذيل الشعاع u إلى رأس الشعاع v:

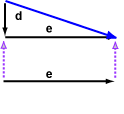
اجمع الشعاعين e و d:

والحل هو:

يوضّح المخطط البياني السابق تحريك الشعاع e للأعلى حتى يلامس ذيله رأس الشعاع d، والناتج هو الشعاع المتشكّل من ذيل الشعاع d إلى رأس الشعاع e .

جمع الأشعة في الفضاء ثلاثي الأبعاد

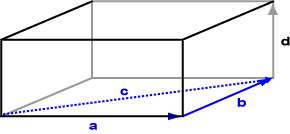
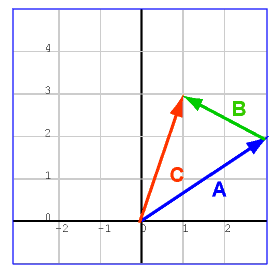
يوضّح المخطط البياني التالي جمع الشعاعين a و b ثلاثيّي الأبعاد لتشكيل الشعاع c. وضعنا الصندوق ثلاثي الأبعاد للمساعدة على تصوّر الأبعاد الثلاثية، إذ تعمل قاعدة الرأس إلى الذيل في الفضاء ثلاثي الأبعاد أيضًا.

تحدّد قاعدة الرأس إلى الذيل مثلثًا مُوجَّهًا في الفضاء ثلاثي الأبعاد عند جمع شعاعين في فضاء ثلاثي الأبعاد.

الخاصية التجميعية Associative لجمع الأشعة

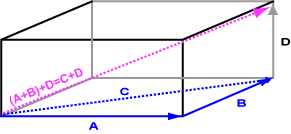
هل يمكن جمع ثلاثة أشعة مثل الأشعة a و b و d في المخطط البياني التالي؟ نعم يمكن ذلك، والنتيجة هي الإزاحة الإجمالية الناتجة عن اتباع كل شعاع بدوره.

يوضّح المخطط البياني التالي نتيجة جمع ‎(a + b) + d = c + d‎، والنتيجة هي شعاع بطول واتجاه مماثل لقطر الشكل.

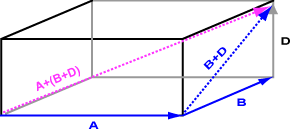
يوضّح المخطط البياني التالي نتيجة جمع ‎a + (b + d)‎، والنتيجة هي نفسها، ويُعَد ذلك دليلًا على الخاصية التجميعية لجمع الأشعة:

a + (b + c) = (a + b) + c

يمكن تطبيق هذه القاعدة في جميع الأبعاد، إذ تكون الأشعة الهندسية للرسوميات الحاسوبية غالبًا ثنائية وثلاثية الأبعاد بالرغم من إمكانية وجود أبعاد أعلى بصورة عامة.

تعني الخاصية التجميعية أنه يمكن كتابة مجموع عدة أشعة مثل: a + b + c + d + e بدون قوسين.

الخاصية التبديلية Commutative لجمع الأشعة

لنفترض أنك تمشي مسافة خمس بنايات شمالًا، ثم ثلاث بنايات شرقًا، ولكن إذا مشيت ثلاث بنايات شرقًا ثم خمس بنايات شمالًا، فهل ستصل إلى المكان نفسه؟ نعم، هذا صحيح.

يُعَد جمع الأشعة عملية تبديلية مثل جمع الأعداد الحقيقية تمامًا:

a + b = b + a

إذا بدأت من النقطة P، فسينتهي بك الأمر في المكان نفسه بغض النظر عن الإزاحة (a أو b) التي ستأخذها أولًا.

سينتج الشعاع c عن كلٍّ من عمليتي الجمع a + b و b + a عند تطبيق قاعدة الرأس إلى الذيل، ولكن هل يمكن تطبيق الخاصية التبديلية على جميع الأبعاد؟ نعم، يمكن ذلك.

تمثيل النقاط باستخدام المصفوفات العمودية

يمكن تمثيل النقاط باستخدام المصفوفات العمودية، ولكن يجب أولًا اتخاذ قرار بشأن الإطار الإحداثي Coordinate Frame الذي يُسمَّى أحيانًا بالإطار فقط. ويتكون الإطار الإحداثي من نقطة مميزة P₀‎ تسمى نقطة الأصل Origin، ومن محور لكل بُعد يُسمَّى X و Y غالبًا، فهناك محوران في الفضاء ثنائي الأبعاد، وثلاثة محاور تُسمَّى X و Y و Z في الفضاء ثلاثي الأبعاد.

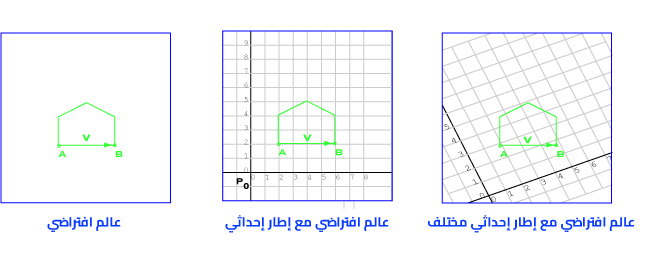
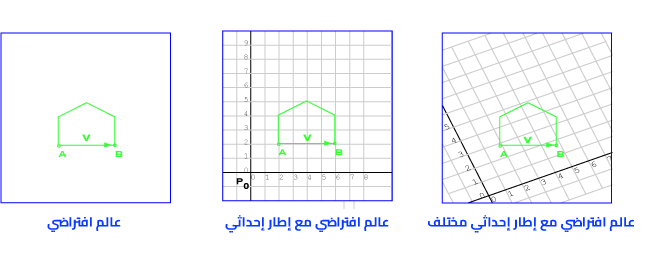
لنبدأ بالفضاء ثنائي الأبعاد، حيث يُظهِر المخطط البياني الأيسر عالمًا افتراضيًا بسيطًا إلى حدٍ ما في فضاء ثنائي الأبعاد، إذ تكون النقاط والأشعة موجودةً في الفضاء بصورة مستقلة عن أيّ إطار إحداثي، بينما يوضّح المخطط البياني الأوسط العالم الافتراضي نفسه مع إطار إحداثي يتكون من نقطة معينة P₀‎ ومحورين، وتُمثَّل النقطة A في هذا الإطار الإحداثي بالمصفوفة العمودية ‎(2, 2)^T‎. يُظهر المخطط البياني الأيمن العالم الافتراضي نفسه مع إطار إحداثي مختلف، إذ تُمثَّل النقطة A في هذا الإطار الإحداثي بالمصفوفة العمودية ‎(2, 3)^T‎.

إذًا، كيف تُمثَّل النقطة B باستخدام الإطار الإحداثي الأول، وباستخدام الإطار الإحداثي الثاني؟ تُمثَّل النقطة B باستخدام الإطار الإحداثي الأول بالمصفوفة العمودية ‎(6, 2)^T‎، وتُمثَّل باستخدام الإطار الإحداثي الثاني بالمصفوفة العمودية ‎(4.8, 1.6)^T‎.

تمثيل النقاط باستخدام إطارات إحداثية مختلفة

الفكرة الأساسية -والمربكة في كثير من الأحيان- هي أنه يوجد في برنامج الرسوميات عالم افتراضي واحد، ولكن قد يكون هناك أيّ عددٍ من الإطارات الإحداثية قيد الاستخدام، إذ لكل كائنٍ إطاره الخاص غالبًا، بحيث يُستخدَم إطار مختلف لوصف مواقع الكائنات؛ ويمكن استخدام إطارٍ آخر لمجال الرؤية، ويُعَد ذلك شيئًا تفعله فعليًا طوال الوقت مع العالم الحقيقي، ولكنه يكون الجزء الصعب في معرفة كيفية العمل مع العالم الافتراضي.

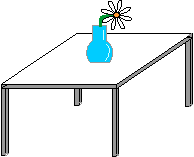
لنفترض أن لديك مزهريةً موضوعةً على طاولة مثلًا، وأنت تتحدث مع صديق عبر الهاتف وترغب في وصف المزهرية له ومكانها وكيف تبدو لك. يمكنك وصف المزهرية بأنها كرة مركزها نقطة الأصل ومتقاطعة مع أسطوانة محورها هو المحور y، ويُعَد ذلك وصفًا للمزهرية في إطارها الخاص. يمكنك وصف موقع المزهرية بأنه "يبعد 20 سم تقريبًا من الحافة الأمامية للطاولة و30 سم من الحافة اليمنى"، واستخدمنا بذلك إطارًا آخر لوصف الموقع.

يمكنك أيضًا التحدث عن كيفية مشاهدتك للطاولة من مسافة 2 متر تقريبًا وارتفاع 1.5 متر، ويستخدم ذلك إطارًا آخر لوصف مجال رؤيتك. يمكن أن تتجول أيضًا حول الطاولة معجبًا بالمزهرية الجميلة، وعندها يجب أن تستخدم إطارًا آخر لوصف مجال رؤيتك الجديد.

لنفترض أنك خرجت للمشي، واقترب منك شخص غريب وسألك عن الاتجاهات إلى مكتب البريد، فما هو إطار الإحداثيات الذي ستستخدمه؟ هل ستستخدم خط العرض وخط الطول استنادًا إلى جرينتش في إنجلترا؟ أم ستستخدم عدد مباني المدينة على يسار ويمين موقعك الحالي؟ حسنًا، إن لم يكن لدى هذا الشخص الغريب جهاز استقبال GPS، فيُرجَّح أن يكون إطار إحداثيات مباني المدينة هو الأكثر فائدة.

تمثيل الأشعة باستخدام المصفوفات العمودية

لنعُد إلى عالمنا الافتراضي، حيث تكون الإزاحة من النقطة A إلى النقطة B هي الشعاع v، ولكن لا يعتمد الشعاع على أيّ نظام إحداثي. يمكن تمثيل الإزاحة باستخدام نظام الإحداثيات الأول (المخطط البياني الأوسط) بأنها:

(الفرق في إحداثيات y, الفرق في إحداثيات x)

وبالتالي تكون الإزاحة هي: ‎(4, 0)^T‎ في هذا المخطط البياني، أي التحرّك بمقدار 4 وحدات من النقطة A باتجاه المحور x للوصول إلى النقطة B، بينما يُمثَّل الشعاع نفسه بالمصفوفة العمودية ‎(2.8, -1.4)^T‎ في نظام الإحداثيات الثاني (الرسم البياني الأيمن).

تُمثَّل كلٌّ من النقاط والأشعة باستخدام المصفوفات العمودية، فهل يُحتمَل أن يكون ذلك مربكًا؟ نعم هذا محتمل، إذ يؤدي هذا الارتباك إلى استخدام الإحداثيات المتجانسة Homogeneous Coordinates، والتي هي طريقة أخرى لتمثيل النقاط والأشعة باستخدام المصفوفات العمودية، ولكننا لن نشرحها في في هذا المقال.

تمثيل جمع الأشعة باستخدام جمع المصفوفات العمودية

إذا كانت الأشعة مُمثلَّة بالمصفوفات العمودية، فسنمثّل جمع الأشعة بجمع المصفوفات العمودية كما يلي:

a = ( 3, 2 )^T

b = ( -2, 1 )^T

a + b = c = ( 1, 3 )^T

يوضح المخطط البياني السابق قاعدة الرأس إلى الذيل المُستخدَمة لجمع الشعاعين a و b للحصول على الشعاع c، وينتج عن جمع المصفوفتين العموديتين a و b المصفوفة العمودية c التي هي التمثيل الصحيح للشعاع c.

تغيير ترتيب معاملات عملية الجمع مع الإجابة نفسها

جرب حساب c = b + a للمصفوفتين العموديتين a و b السابقتين نفسهما، وستكون الإجابة نفسها هي:

b + a = c = ( 1, 3 )^T

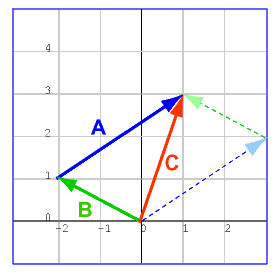
اتبع الخطوات التالية التي يكون فيها الشعاع b بمثابة شعاع البداية لإنشاء الرسم البياني التالي:

1. ارسم الشعاع الأول b على شكل سهم، بحيث يكون ذيله عند نقطة الأصل.
2. ارسم الشعاع الثاني a على شكل سهم، بحيث يكون ذيله عند نقطة رأس الشعاع الأول.
3. يكون مجموعهما هو السهم المتشكّل من نقطة الأصل إلى رأس الشعاع الثاني.

ملاحظة: تذكّر أن الأشعة ليس لها موقع محدّد، لذا يمكنك رسم مثيل للشعاع بحيث يبدأ ذيله من أيّ نقطة تريدها.

يجب أن تكون نتيجة الجمع هي نفسها بما أن جمع الأشعة عملية تبديلية.

تذكير: تُعَد عملية جمع الأشعة وجمع المصفوفات العمودية عملية تجميعية أيضًا.

تدريب عملي

ليكن لدينا الشعاعان:

R = ( 4, 3 )^T

S = ( 1, 2 )^T

أوجد ناتج عملية الجمع:

T = R + S

يمكنك إيجاد الناتج من خلال استخدام جمع المصفوفات العمودية وقاعدة الرأس إلى الذيل، وسيكون الناتج عند تطبيق القاعدة هو:

T = (5, 5)^T

ولنجمع الآن الشعاعين بترتيب معاكس كما يلي:

T = S + R

حيث يكون الشعاعان هما:

S = ( 1, 2 )^T

R = ( 4, 3 )^T

وتبقى الإجابة نفسها:

T = (5, 5)^T

استخدام متوازي الأضلاع في عملية جمع الأشعة

هناك طريقتان لتشكيل عملية الجمع:

T = S + R

T = R + S

حيث يكون الشعاعان هما:

R = ( 4, 3 )^T

S = ( 1, 2 )^T

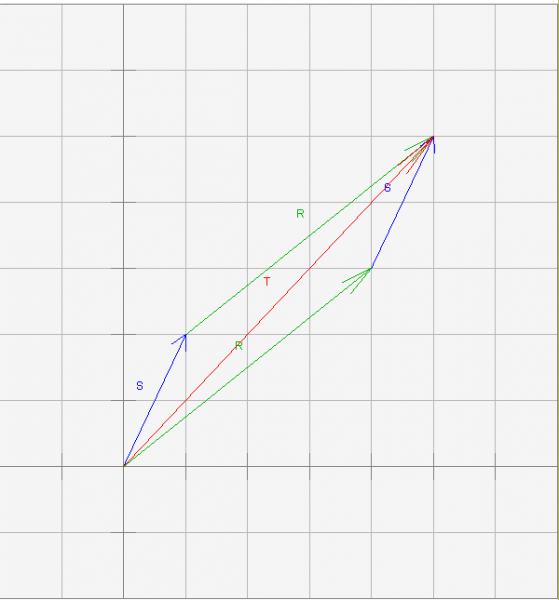
هناك طريقتان للرسم اعتمادًا على ذيل السهم الذي تضعه عند نقطة الأصل، بحيث إذا استخدمتَ كلا الطريقتين، فستحصل على متوازي أضلاع مع ناتج جمع الأشعة الذي يُمثَّل بسهم قطري يبدأ ذيله من نقطة الأصل.

قد تتساءل عن ما هو متوازي الأضلاع Parallelogram وعمّا إذا كانت مادة الهندسة التي تعلّمتها في المدرسة الثانوية غامضة قليلًا، فمتوازي الأضلاع هو شكل رباعي فيه كل ضلعين متقابلين متوازيين ومتساويين في الطول، مثل السهمين الأزرقين الممثلين للشعاع s اللذين لهما الطول والاتجاه نفسه، والسهمين الأخضرين الممثلين للشعاع r اللذين لهما الطول والاتجاه نفسه.

رحلة ثنائية الاتجاه

أوجد ناتج ما يلي:

w = u + v

إذا كان:

u = ( -3, 2 )^T

v = ( 1, -5 )^T

والجواب هو:

w = ( -2, -3 )^T

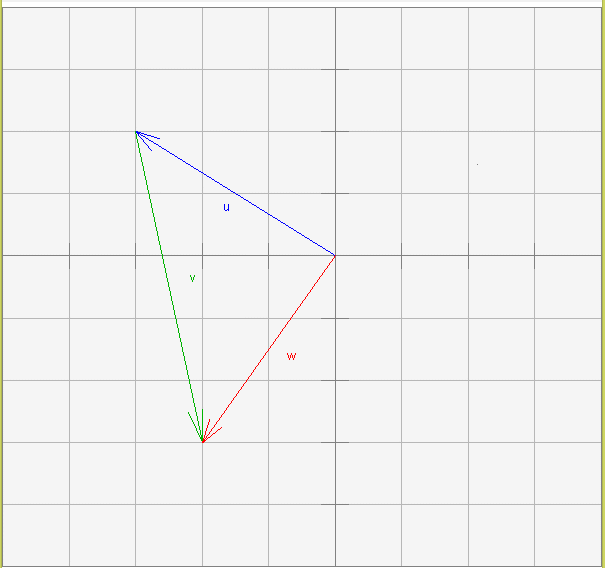
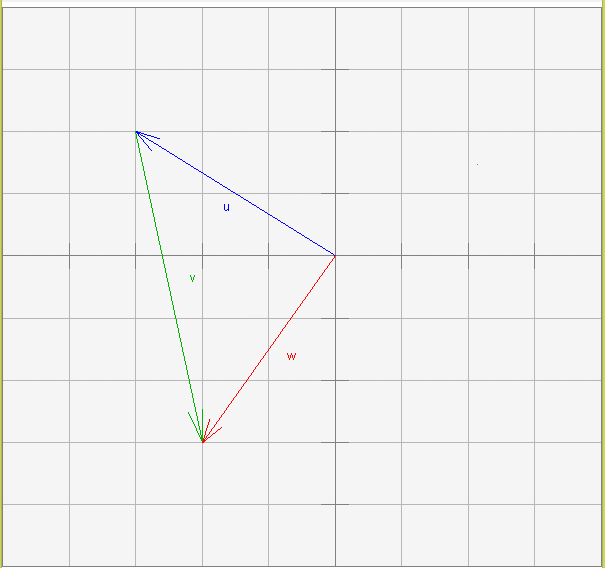
يوضح المخطط البياني السابق عملية الجمع w= u + v.

لنفترض أن نملةً ما تبدأ التحرك من نقطة الأصل وتسير على طول الشعاع u، ثم تسير على طول الشعاع v حتى تصل إلى رأس الشعاع w، وتبدأ النملة الثانية من نقطة الأصل وتسير على طول الشعاع w حتى تصل إلى نهايته، وبالتالي ستصل كلتا النملتين إلى النقطة نفسها.

جمع الإزاحات وجمع الأطوال غير متساويين

هل مشت النملتان المسافة نفسها في المثال السابق؟ في هذه الحالة، لا! فمن الواضح أن المشي في خط مستقيم إلى الوِجهة النهائية أقصر.

لا يُعَد جمع الإزاحات (أو الأشعة) مثل جمع أطوالها، إذ ينتج عن جمع الشعاعين u و v شعاع أقصر من طول الشعاع u مع طول الشعاع v في المثال السابق؛ ويمكنك ملاحظة ذلك حاليًا من خلال النظر إلى المخطط البياني السابق، وتذكّر أن "الخط المستقيم هو المسافة الأقصر بين نقطتين" (سنناقش ذلك لاحقًا باستخدام صيغة فيثاغورس).

تسمى هذه الحقيقة الرياضية بمتراجحة المثلث Triangle Inequality، وهي تنص على أن ناتج جمع أي طولين من أضلاع المثلث أكبر من طول الضلع الثالث.

طول (v + u) <= طول (u) + طول (v)

إليك حالة يكون فيها طول ناتج الجمع أقصر بكثير من مجموع الأطوال:

e = ( 5, 4 )^T

g = ( -4.9, -3.9 )^T

e + g = (0 .1, 0.1 )^T

ملاحظة: نقلنا الشعاع g قليلًا من المكان الذي ينبغي أن يكون فيه للتوضيح.

الأشعة ذات الاتجاه نفسه

هل يمكنك التفكير في حالة يكون فيها طول ناتج الجمع مساويًا لمجموع طولي شعاعي الدخل؟ نعم يمكن ذلك إذا كان لأحد الشعاعين اتجاه الشعاع الآخر.

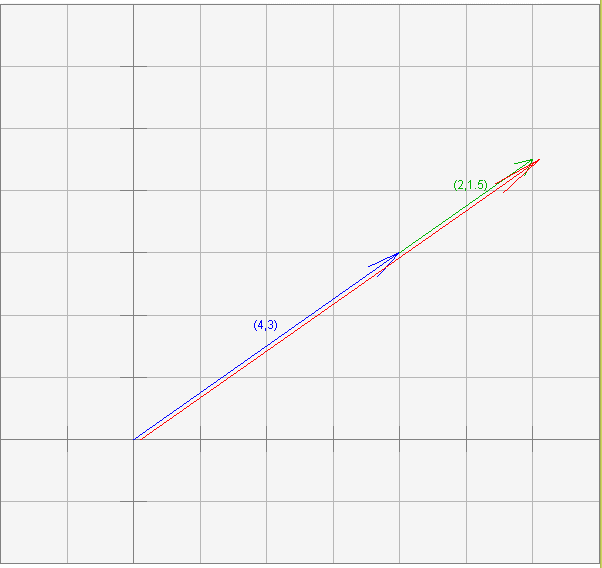
يمكن توضيح هذه الحالة في المخطط البياني التالي، إذ تُستخدَم قاعدة الرأس إلى الذيل لجمع شعاعين يؤشّران إلى الاتجاه نفسه، وتُسمَّى الأشعة ذات الاتجاه نفسه بأنها مرتبطة خطية Collinear. نقلنا شعاع ناتج الجمع قليلًا عن مكانه الصحيح حتى تتمكّن من رؤيته.

بعد ذلك جمعنا الشعاعين ‎(4, 3)^T‎ و ‎(2, 1.5)^T‎، والناتج هو ‎(6, 4.5)^T‎. يمكنك حاليًا تحديد ما إذا كان هناك شعاعان لهما الاتجاه نفسه من خلال النظر إلى الصورة أو باستخدام المفاهيم الهندسية، وستتعرّف لاحقًا على إجراءٍ لاختبار ما إذا كان هناك شعاعان يؤشّران إلى الاتجاه نفسه.

يعبِّر هذا المثال عن حالةٍ تطبِّق إشارة المساواة "=" الموجودة في الصيغة التالية:

طول (v + u) <= طول (u) + طول (v)

جمع الأشعة الصفرية

هل يمكنك التفكير في حالةٍ أخرى تطبّق إشارة المساواة "=" الموجودة في الصيغة السابقة؟ نعم، عندما يكون أحد الشعاعين شعاعًا صفريًا كما يلي:

طول ‎(0 + u)‎ <= طول (u) + طول (0)

اجمع المصفوفة الصفرية ‎( 0, 0 )^T‎ مع المصفوفة ‎( 4, 3 )^T‎، فإذا مثّلت المضفوفة ‎( 0, 0 )^T‎ شعاع إزاحة، فهذا يعني عدم تطبيق أيّ شيء لتغيير موضع الشعاع الآخر.

جمع النقاط والأشعة

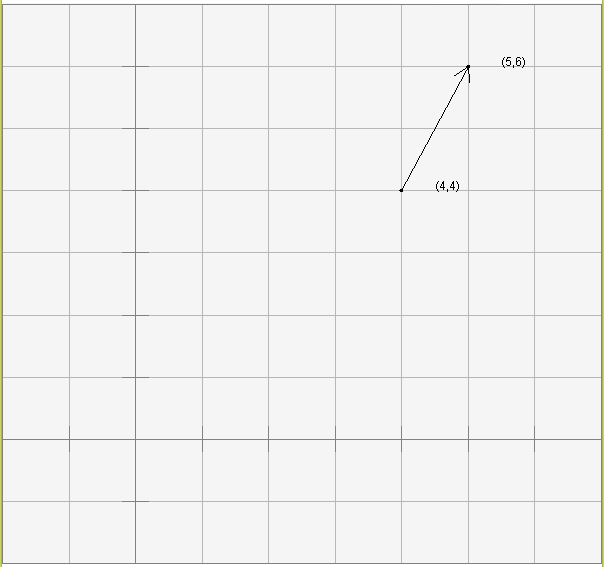
لنفترض أنك تريد جمع الشعاع ‎(1, 2)^T‎ والنقطة ‎(4, 4)^T‎. إذا كان ذلك منطقيًا، فأجرِ هذه العملية، وما هو نوع الكائن الناتج؟ يكون الناتج نقطة كما يلي:

‭‭(4, 4)^T + (1, 2)^T = ( 5, 6 )^T

إذا كان الشعاع ‎(1, 2)^T‎ إزاحة (أي مقدار يمكن تغيير قيمة x به، ومقدار يمكن تغيير قيمة y به)، فيجب أن تكون النتيجة نقطة في موقع جديد كما يلي:

‭(4, 4)^T + (1, 2)^T = ( 5, 6 )^T

هذه إحدى الحالات التي يكون فيها استخدام التمثيل (أي المصفوفات العمودية) نفسه لكل من النقاط والأشعة أمرًا مربكًا، لذا يجب عليك تتبّع نوع الكائن الذي تمثله كل مصفوفة.

تنتج نقطةٌ عن جمع شعاع إزاحة ونقطة كما في المخطط البياني التالي:

يُعَد جمع كائنين رياضيين من نوعين مختلفين غريبًا قليلًا، ولا تنسَ أن إشارة الجمع "+" إشارة قابلة للتحميل الزائد overloaded.

الانسحاب Translation

تُسمَّى عملية جمع شعاع ونقطة بالانسحاب Translation، ويُقال أحيانًا أن النقطة الأصلية مسحوبةً إلى موقع جديد.

قد تكون المصطلحات هنا مربكةً قليلًا، إذ ينتج عن جمع شعاع ونقطة من الناحية الرياضية نقطةٌ جديدة، بحيث تبقى النقطة الأولى دون تغيير، ولكن من الجيد التفكير في الصور "التي تتحرك عبر الشاشة" عند جمع أشعة الإزاحة والنقاط الخاصة بها في مصطلحات الرسوميات الحاسوبية، لذا قد تسمع أحيانًا مصطلحات مثل "تحريك نقطة" و"النقطة القديمة" و"النقطة الجديدة".

لقد رأينا تطبيق العمليات التالية:

• شعاع + شعاع.
• نقطة + شعاع.
• نقطة - نقطة.

فهل تفترض أنه يمكن إجراء العملية نقطة + نقطة؟ لا يُعَد جمع نقطتين شيئًا هندسيًا. يمكنك تشكيل مجموع شعاعين عموديين يمثلان نقاطًا ميكانيكيًا، ولكن النتيجة لا تكون ذات معنى فعلي.

لقد وصلنا إلى نهاية هذا المقال، وسنناقش في المقال التالي العمليات على الأشعة بصورة أكبر، وسنناقش لاحقًا مزيدًا من العمليات على الأشعة.

ترجمة -وبتصرُّف- للفصل Vector Addition من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.

اقرأ أيضًا

• المقال السابق: كيفية جمع وطرح المصفوفات العمودية والمصفوفات السطرية
• الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد
• التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد