سنناقش في هذا المقال كيفية جمع وطرح المصفوفات العمودية والسطرية ولكن لنتعرّف على بعض المصطلحات التي سنستخدمها:
- النقطة Point: كائن هندسي، وهو موقع في فضاء ثلاثي الأبعاد أو ثنائي الأبعاد.
- الشعاع Vector: كائن هندسي له خصائص الاتجاه والطول، ولكن ليس لديه خاصية الموقع.
- المصفوفة العمودية Column Matrix: قائمة مرتبة من الأعداد تُرتَّب ضمن عمود.
- المصفوفة السطرية Row Matrix: قائمة مرتبة من الأعداد تُرتَّب ضمن صف.
- العنصر Element: أحد الأعداد التي تشكل المصفوفة العمودية أو السطرية.
- البعد Dimension: عدد العناصر في مصفوفة عمودية أو سطرية.
- الإزاحة Displacement: هو الفرق بين موقعين، ويعبَّر عنه باستخدام شعاع.
كما سنوضّح في هذا المقال المواضيع التالية:
- منقول Transpose المصفوفة العمودية أو السطرية.
- جمع المصفوفات العمودية والمصفوفات السطرية.
- الخاصية التبديلية لجمع المصفوفات.
- الخاصية التجميعية لجمع المصفوفات.
- طرح المصفوفات العمودية والمصفوفات السطرية.
- الخاصية غير التبديلية لطرح المصفوفات.
منقول مصفوفة Transposition
ماذا تُسمَّى عملية قَلب مصفوفة العمودية، أو ماذا تُسمَّى عملية قَلب مصفوفة سطرية إلى مصفوفة عمودية؟ تسمّى عملية المنقول Transposition.
تُعَد المصفوفة السطرية والمصفوفة العمودية من نوعين مختلفين حتى لو كان لهما البعد نفسه وتحتويان على العناصر نفسها، لذا يُستخدَم الحرف العُلوي "T" عند كتابة مصفوفة عمودية مثل صفٍ من الأعداد، إذ يكون العنصر الأول في المصفوفة العمودية هو العنصر الموجود أعلى العمود، ويكون العنصر الأول في المصفوفة السطرية هو العنصر الموجود على يسار الصف.
سنوضح فيما يلي طريقتين لكتابة المصفوفة العمودية نفسها، إذ تُكتَب عناصر المصفوفة العمودية بالطريقة نفسها بغض النظر عن كيفية عرض المصفوفة العمودية.
يعني وجودُ حرف T العُلوي في المصفوفة العمودية قلبَ العمود إلى صف، وينتج عنه مصفوفة سطرية، وتستخدم بعض الكتب حرف t صغير.
ما هو : (1, 2, 3)T T؟
( 1, 2, 3 )T T = ( 1, 2, 3 )
يؤدي تطبيق المنقول مرتين إلى العودة إلى ما بدأت به. يبدو هذا واضحًا الآن، ولكن قد يكون من المفيد تذكّر ذلك لاحقًا عند تطبيق المعالجة الجبرية.
جمع المصفوفات العمودية
يمكن جمع مصفوفتين عموديتين لهما البُعد نفسه، وتنتج مصفوفة عمودية لها البعد نفسه أيضًا، وينطبق الشيء نفسه على المصفوفات السطرية.
تُطبَّق عملية الجمع من خلال جمع العناصر المتقابلة لمصفوفات الدخل لإنتاج العناصر المقابلة لمصفوفة الخرج كما يلي:
( 42, -12 )T + ( 8, 24 )T = ( 50, 12 )T
( 32.98, -24.71, 9.392 )T + ( -32.98, +24.71, -9.392 )T = (0, 0, 0)T
( 9.2, -8.6, 3.21, 48.7 ) + ( -2.1, 4.3, 1.0, 2.3 ) = ( 7.1, -4.3, 4.21, 51.0 )
( 1, 2, 3 ) + ( 10, 20, 30 ) = ( 11, 22, 33 )
إذا كان a و b مصفوفتين من النوع نفسه، فإن a + b = c يعني أن كل عنصر ci = ai + bi
أوجد ناتج ما يلي: ( 2, -2 )T + ( 8, 6 )T
الجواب:
( 2, -2 )T + ( 8, 6 )T = ( 10, 4 )T
جمع المصفوفات ثلاثية الأبعاد
يجب أن تكون المصفوفات التي تجمعها لها البُعد والنوع نفسه سواءً كانت عمودية أم سطرية. يجري التعامل مع كل بُعد بصورة مستقلة عن الأبعاد الأخرى عند جمع المصفوفات، فمثلًا سيكون لديك ثلاث عمليات جمع منفصلة باستخدام العمليات الحسابية العادية عند جمع مصفوفتين عموديتين ثلاثيتي الأبعاد، إذ تُجمَع العناصر الأولى من المصفوفات التي تمثل معاملات عملية الجمع لتكوين العنصر الأول من المصفوفة الناتجة.
أوجد ناتج ما يلي: ( 8, 4, 6 )T + ( 2, -2, 9 )T
( 2, -2, 9 )T + ( 8, 4, 6 )T
الجواب:
( 8, 4, 6 )T + ( 2, -2, 9 )T = ( 10, 2, 15 )T
( 2, -2, 9 )T + ( 8, 4, 6 )T = ( 10, 2, 15 )T
الخاصية التبديلية Commutative لجمع المصفوفات
تُعَد عملية جمع المصفوفات عملية تبديلية، أي أن: a + b = b + a، وينطبق ذلك على المصفوفات السطرية والعمودية بجميع أبعادها، إذ يمكن القول أن: a + b + c = b + c + a = c + a + b = …...
تعني الخاصية التبديلية أن ترتيب جمع المصفوفات غير مهم، إذ تعمل المصفوفات باستخدام طريقة عمل الأعداد نفسها بالنسبة للجمع: 1 + 2 = 2 + 1، فالمصفوفات والأعداد عادةً لا تعمل بالطريقة نفسها ولكنها كذلك بالنسبة لعملية الجمع.
أوجد ناتج ما يلي: ( -1, -2, 3 )T + ( 1, 2, -3 )T
الجواب:
( -1, -2, 3 )T + ( 1, 2, -3 )T = ( 0, 0, 0 )T
المصفوفة العمودية الصفرية
ليكن لدينا مثلًا مصفوفة صفرية كما يلي:
( 73.6, -41.4 )T + ( 0.0, 0.0 )T = (73.6, -41.4 )T
تُسمَّى المصفوفة التي تكون جميع عناصرها أصفارًا بالمصفوفة الصفرية Zero Matrix، ويكون ناتج جمع المصفوفة الصفرية والمصفوفة a لهما النوع نفسه
هو المصفوفة a.
نرمّز المصفوفة الصفرية بالرمز 0 (صفر بالخط العريض) الذي يختلف عن 0 (العدد الحقيقي صفر)، ويحدّد السياق الذي ترى فيه الرمز 0 ما إذا كانت مصفوفة صفرية سطرية أم عمودية وعدد العناصر التي تحتوي عليها. فإذا رأيت (73.6, -41.4 )T + 0 ، فيمكنك أن تفترض ما هو النوع الصحيح للمصفوفة 0 والمناسب للتعبير.
الخاصية التجميعية Associative لجمع المصفوفات
أوجد ناتج ما يلي: ( 2, 5, -9 ) + ( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 )
الجواب:
( 2, 5, -9 ) + ( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 ) =
( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 ) + ( 2, 5, -9 ) =
----------------------------
( -32.034, 94.79, 201.062 ) + ( 0, 0, 0) =
( -32.034, 94.79, 201.062 )
قد يفقد بعض الطلاب صبرهم عندما يجمّعون المصفوفتين الأوليتين، ثم يجمّعون الناتج مع المصفوفة الثالثة، ولكن يدرك بعضهم أنه يمكن إعادة ترتيب المصفوفات إلى ترتيب أكثر ملاءمة بما أن جمع المصفوفات يُعَد عملية تبديلية، إذ يمكنهم اختيار عملية الجمع "+" التي يريدون تطبيقها أولًا بعد أن تصبح المصفوفات في ترتيب مناسب.
يُعَدّ جمع المصفوفات عملية تجميعية، وهذا يعني أن:
( a + b ) + c = a + ( b + c )
أي يمكن جمع المصفوفتين a و b ثم جمع النتيجة مع المصفوفة c، وستكون النتيجة النهائية هي نفسها كما لو جمعت المصفوفة a إلى نتيجة جمع المصفوفتين b و c. يمكن تطبيق ذلك على المصفوفات السطرية والعمودية بجميع أبعادها.
هل يمكنك إيجاد ناتج ما يلي في الوقت المناسب؟
( 25.1, -19.6 ) + ( -5.0, 9.0 ) + ( 12.4, 8.92 ) + ( -20.1, 10.6 )
الجواب:
( 25.1, -19.6 ) + ( -5.0, 9.0 ) + ( 12.4, 8.92 ) + ( -20.1, 10.6 ) =
------------- ---------------
\ /
\ /
\ /
\ /
( 25.1, -19.6 ) + ( 12.4, 8.92 ) + ( -25.1, 19.6 )
--------------- ---------------
\ /
\ /
\ /
\ /
\ /
( 0.0, 0.0 ) + ( 12.4, 8.92 ) = ( 12.4, 8.92 )
بعض الأشياء التي لا يمكن استخدامها عند جمع المصفوفات
يعني الرمز "+" زيادة التحميل Overloaded في مصطلحات علوم الحاسوب، مما يعني أن العملية المُستدعاة تعتمد على نوع المعاملات، فمثلًا:
- يعني الرمز + هنا جمع أعداد حقيقية: 1.34 + -9.06
- يعني الرمز + هنا جمع مصفوفات عمودية: ( 84.02, 90.31 )T + ( -14.23, 10.85 )T
بينما لا تعطي الأمور التالية أيّ معنًى:
- لا يمكن جمع عدد ومصفوفة: 34.5 + ( 84.02, 90.31 )T
- لا يمكن جمع مصفوفة سطرية ومصفوفة عمودية: ( 84.02, 90.31 ) + ( -14.23, 10.85 )T * لا يمكن جمع مصفوفات ذات أبعاد مختلفة: ( 84.02, 90.31 ) + ( -14.23, 10.85, 32.75 )
تكون هذه المشاكل واضحة عند كتابة العناصر كما سبق، ولكنها تكون أقل وضوحًا عند استخدام الرموز المتغيرة كما يلي:
- لا يمكن جمع عدد ومصفوفة a + x.
- يجب التأكد من أن المعاملين x + y من النوع نفسه.
يمكن إجراء عملية الجمع: ( 4.5, x1, w ) + ( -2.3, 3, y2 ) كما يلي:
( 4.5, x1, w ) + ( -2.3, 3, y2 ) = ( 2.2, x1 +3, w+ y2 )
طرح المصفوفات
يمكن طرح مصفوفتين من النوع نفسه وتنتج مصفوفة ثالثة من ذات النوع، إذ يمكن طرح مصفوفتين من خلال طرح العناصر المتقابلة، مع الحرص على إبقاء العناصر بالترتيب نفسه كما يلي:
(10, 8, 12 ) - (2, 14, 9 ) = ( 10 - 2, 8 - 14, 12 - 9 ) = ( 8, -6, 3 )
إذا كانت a و b مصفوفتان من النوع نفسه، فإن a - b = c تعني أن كل عنصر ci = ai - bi
ليست عملية الطرح تبديلية
أوجد ناتج ما يلي:
(22, 5, -12 ) - (10, -5, 3 ) (10, -5, 3 ) - (22, 5, -12 )
الجواب:
(22, 5, -12 ) - (10, -5, 3 ) = ( 22 - 10, 5 - (-5), -12 - 3 ) = ( 12, 10, -15 )
(10, -5, 3 ) - (22, 5, -12 ) = ( 10 - 22, (-5) - 5, 3 - (-12) ) = (-12, -10, 15 )
حقيقة رياضية: لا تُعَد عملية الطرح تبديلية، وهذا يعني أنه لا يمكنك تغيير الترتيب عند طرح المصفوفتين a - b.
يمكن إيجاد معاكس مصفوفة -a من خلال إيجاد معاكس كل عنصر من عناصر هذه المصفوفة كما يلي:
-(22, 5, -12 ) = ( -22, -5, 12 )
-( 19.2, 28.6, 0.0 )T = ( -19.2, -28.6, 0.0 )T
يمكن القول أنه إذا كانت a هي ( a0, a1, …, a2) فإن -a تعني (-a0, -a1, …, -a2).
إدخال الإشارة السالبة داخل الأقواس
أوجد ناتج عملية الطرح التالية: ( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T
الجواب:
( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T =
( -7.2 -(-2.2), -98.6 -(-2.4), 0.0 - 3.0)T =
( -5.0, -96.2, - 3.0)T
ولكن قد تجد أن الطريقة التالية أسهل للحل:
( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T =
( -7.2, -98.6, 0.0 )T + ( +2.2, +2.4, -3.0 )T =
( -5.0, -96.2, - 3.0)T
اُستخدِمت الإشارة السالبة الخارجية لعكس إشارة المصفوفة الثانية، ثم تُجمَع المصفوفتان الناتجتان كما يلي:
a - b = a + (-b)
قد يكون من المفيد تذكّر ذلك، حيث يمكنك عكس إشارة المصفوفات بحيث تكون العملية هي جمع المصفوفات ثم إعادة ترتيب عملية الجمع لأن عملية الجمع تُعَد عملية تبديلية:
a - b + c - d = a + (-b) + c + (-d) = (-d) + a + c + (-b) = الجمع بأيّ ترتيب تريده
إليك بعض الحقائق الأخرى:
a + (-a) = 0 a - a = 0
لاحظ أن 0 هي المصفوفة الصفرية، ولها نوع المصفوفة a نفسه ولكن تكون جميع عناصرها صفر.
أجرِ العملية التالية:
( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) - ( 4, -5, -4.8 )
حاول إعادة الترتيب بدلًا من التسرع والحساب مباشرةً:
( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) - ( 4, -5, -4.8 ) = ( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) + ( -4, 5, 4.8 ) = ( 4, -5, 6.2 ) + ( -4, 5, 4.8 ) + ( -43.132, 13.6, 86.5 ) = ( 0, 0, 11 ) + ( -43.132, 13.6, 86.5 ) = (-43.132, 13.6, 97.5 )
وقد تتخطى بعض الخطوات إذا حاولت الحساب ذهنيًا.
تدريب عملي
أولًا، ما هو مجموع الإزاحات الثلاثة التالية:
d = ( -12.4, 14.8, 0.0 )T
e = ( 6.2, -10.2, 17.0 )T
f= ( 6.2, -4.6, -17.0 )T
والناتج هو:
(0.0, 0.0 0.0)T.
ثانيًا، أوجد قيمة x و y و z بحيث يكون ما يلي صحيحًا:
a = ( 8.6, 7.4, 3.9 )
b = ( 4.2, 2.2, -3.0 )
c = ( x, y, z )
a + b + c = 0
وبالتالي يمكن كتابة ما يلي:
a + b + c = ( 12.8, 9.6, 0.9 ) + (x, y, z) = ( 12.8+x, 9.6+y, 0.9+z ) = (0, 0, 0)
لذا يجب أن يكون:
12.8 + x = 0; x = -12.8
9.6 + y = 0; y = -9.6
0.9 + z = 0; z = -0.9
استخدام الجبر في جمع وطرح المصفوفات
كان التمرين السابق هو العثور على عناصر المصفوفة c عندما: a** + b + c = 0**، ولكن إن لم تكن على علمٍ أنها مصفوفات، فقد تميل إلى حل هذا التمرين باستخدام جبر الأعداد الحقيقية real كما يلي:
a + b + c = 0
a + b = -c + 0
(a + b) = -c
-(a + b) = c
يمكن استخدام هذه الطريقة طالما أن المصفوفات من النوع نفسه، والعمليات هي جمع "+" أو طرح "-" فقط، وبالتالي يمكنك التظاهر بأنك تطبّق عمليات جبرية عادية. لاحظ أن المعادلة الأخيرة تعني "اجمع a مع b، ثم اعكس إشارة النتيجة لتحصل على c".
لنتعمق أكثر ولننظر فقط إلى العناصر الأولى من المصفوفات:
( a0, … ) + ( b0, … ) + ( c0, … ) = ( 0, …)
( a0, … ) + ( b0, … ) = -( c0, … ) + ( 0, …)
( a0, … ) + ( b0, … ) = -(c0, … )
( a0 + b0, … ) = -( c0, … )
-( a0 + b0, … ) = ( c0, … )
-( a0 + b0) = c0
إذا كان ذلك غير منظم بالنسبة لك، فامسح ذهنيًا بعض الأشياء غير المرغوب فيها كما يلي:
a0 + b0 + c0 = 0
a0 + b0 = -c0 + 0
a0 + b0 = -c0
a0 + b0 = -c0
-( a0 + b0) = c0
وتتبع العناصر الأخرى النمط نفسه، وبالتالي تكون النتيجة صحيحة بالنسبة للمصفوفة ككل.
أوجد قيمة c1 و c0 بحيث يكون ما يلي صحيحًا:
a = ( -4, 2 )T
b = ( 8, 3 )T
c = ( c0, c1 )T
a + b + c = 0
ويكون الحل باستخدام الطريقة التالية:
a + b + c = 0
a + b = -c
( 4, 5 )T = -( c0, c1 )T
-( 4, 5 )T = ( c0, c1 )T
(-4, -5 )T = ( c0, c1 )T
وبالتالي:
c0 = -4
c1 = -5
وصلنا إلى نهاية المقال الذي تعلّمنا من خلاله كيفية جمع وطرح المصفوفات وسنوظّف هذه المعرفة في المقال التالي لتعلّم كيفية جمع [الأشعة](رابط المقال التالي).
ترجمة -وبتصرُّف- للفصل Matrix Addition من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.


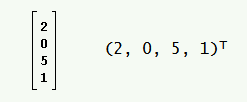












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.