تُستخدَم عملية ضرب المصفوفات في الرسومات الحاسوبية من أجل إنشاء مصفوفات التحويل Transformation التي تُطبَّق على النقاط والأشعة. وتُصمَّم المناظر في الألعاب ذات نمط منظور الشخص الأول First Person Game مثل لعبة DOOM باستخدام النقاط والأشعة أيضًا، كما ينشأ العرض المتغير الذي نراه أثناء تحرّك اللاعب عبر هذه المناظر بتحويل تلك النقاط والأشعة.
ونظرًا لأهمية المصفوفات في مجال النقاط والأشعة التي بدورها تتداخل مباشرةً مع عملية إنشاء تصاميم ثلاثية الأبعاد، فسنفصل في هذا المقال في كيفية التعامل مع المصفوفات وضربها ببعضها.
لقد تحدثنا في المقال السابق عن كيفية ضرب المصفوفات بمصفوفة عمودية، ولمعرفة كيفية التعامل مع المصفوفات أكثر، سنناقش بهذا المقال مفهوم ضرب المصفوفات وخاصيتها وكيفية حسابها لعمل تصاميم ثلاثية الأبعاد 3D؛ وسنتحدث عما يلي:
- متى نضرب المصفوفات
- ناتج ضرب المصفوفات
- نتاج كل عنصر من عناصر المصفوفة المحصل عليها بتطبيق عملية جداء نقطي
- الخاصية التجميعية لضرب المصفوفات
- الخاصية غير التبديلية لضرب المصفوفات
- توزيع ضرب المصفوفات على عملية الجمع
- الضرب بالمصفوفة الصفرية
أبعاد نتيجة ضرب المصفوفات
يمكن ضرب المصفوفتين A4×3 و B3×5 عند تطابق البعد الداخلي الذي قيمته 3؛ فإذا رتبنا مصفوفتين مستطيلتين بحيث يكون البعد الداخلي لكل منهما متساويًا، فيمكن ضرب هاتين المصفوفتين، وستكون النتيجة عمومًا عبارة عن مصفوفة مستطيلة كالآتي:
AR×N BN×C = ZR×C
تحتوي عملية الضرب AB -إذا كان تشكيلها ممكنًا- على نفس عدد صفوف المصفوفة A وعلى نفس عدد أعمدة المصفوفة B؛ وهنا إذا لم نتمكن من تجاهل البعد الداخلي، فلن نتمكن من تشكيل عملية الضرب.
فلنطّلع الآن على المثال التالي، مع تجاهل كيفية حساب العناصر مبدئيًا؛ إذ سنضرب مصفوفةً أبعادها 3×2 في مصفوفة أخرى أبعادها 2×2، والنتيجة ستكون عبارة عن مصفوفة أبعادها 3×2:
انطلاقًا مما سبق، نستطيع القول أن أبعاد نتيجة ضرب المصفوفتين A4×4 B4×2 مثلًا، ستكون:
A4×4 B4×2 = C4×2
ملاحظة: تُعَد المصفوفات العمودية والمصفوفات السطرية حالة خاصة من المصفوفات المستطيلة، لذا فإن قاعدة أبعاد نتيجة ضرب المصفوفات تسري عليها أيضًا.
لنتدرب الآن على مزيدٍ من الأمثلة في الجدول التالي؛ إذ سنحدّد أبعاد نتيجة ضرب كلّ زوج من المصفوفات:
| أبعاد المصفوفة الأولى | أبعاد المصفوفة الثانية | النتيجة |
|---|---|---|
| 4 × 3 | 3 × 2 | 4 x 2 |
| 2 × 3 | 2 × 3 | غير ممكنة |
| 3 × 5 | 5 × 1 | 3 x 1 |
| 3 × 2 | 2 × 2 | 3 x 2 |
| 4 × 3 | 3 × 1 | 4 x 1 |
| 3 × 1 | 1 × 4 | 3 x 4 |
ملاحظة: سنحتاج للتحقق دائمًا من أبعاد نتيجة ضرب المصفوفات قبل إجراء العمليات الحسابية؛ فمثلًا، عملية الضرب الأخيرة في الجدول السابق غريبة بعض الشيء، ومن السهل أن يختلط علينا الأمر دون معرفة الشكل الذي يجب أن تبدو عليه النتيجة.
يمكننا تشكيل عملية الضرب An×m Bm×p، ولكن لا يمكننا تشكيل عملية الضرب Bm×p An×m إذا كانت n ≠ p. وسيتضح لاحقًا أنه حتى لو أمكن تشكيل كلتا عمليتي الضرب، فمن النادر أن يكون AB = BA.
تشكيل عملية ضرب المصفوفات
يُحسَب حاصل ضرب مصفوفتين AB من خلال تطبيق الجداء النقطي على كل صف من المصفوفة A مع كل عمود من المصفوفة B، بحيث يكون عدد الأعمدة في المصفوفة A مساويًا لعدد الصفوف في المصفوفة B.
لنجرب قلب أحد أعمدة المصفوفة B بحيث تصبح عناصره محاذيةً لصفوف المصفوفة A، ثم نطبّق عليها الجداء النقطي؛ وهنا سينتج لدينا العنصر الموجود في الصف 1 والعمود 1 من المصفوفة الناتجة. لننتقل بعدها إلى الصف التالي مع تطبيق الجداء النقطي، لينتج لدينا العنصر الموجود في الصف 2 والعمود 1 من المصفوفة الناتجة؛ وسنستمر بهذه العملية حتى الوصول إلى الصف الأخير.
لننتقل الآن إلى العمود التالي ونقوم بنفس الشيء عند الانتهاء من العمود الأول من المصفوفة B، ونواصل تطبيق ذات الشيء على كل عمود من المصفوفة B حتى حساب جميع العناصر.
ملاحظة: العنصر ij من المصفوفة الناتجة = الجداء النقطي للصف i من المصفوفة A مع العمود j من المصفوفة B.
لنفترض أننا نشكّل عملية الضرب التالية:
A5×3 B3×2 = C5×2
سنستخدم الصف الثالث من المصفوفة A والعمود الثاني من المصفوفة B، لحساب الصف الثالث، والعمود الثاني من المصفوفة الناتجة C.
طريقة أخرى لتصور عملية ضرب المصفوفات
قد تعرض كتب الرسوميات الحاسوبية طريقةً مختلفةً لضرب المصفوفات؛ إذ أن هناك عدة طرق للتفكير في الأمر بالرغم من أن النتائج هي نفسها.
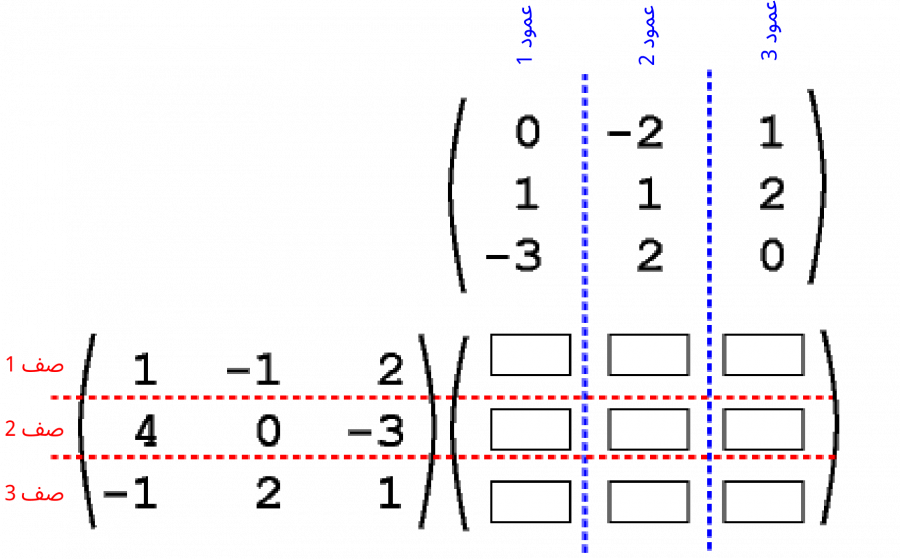
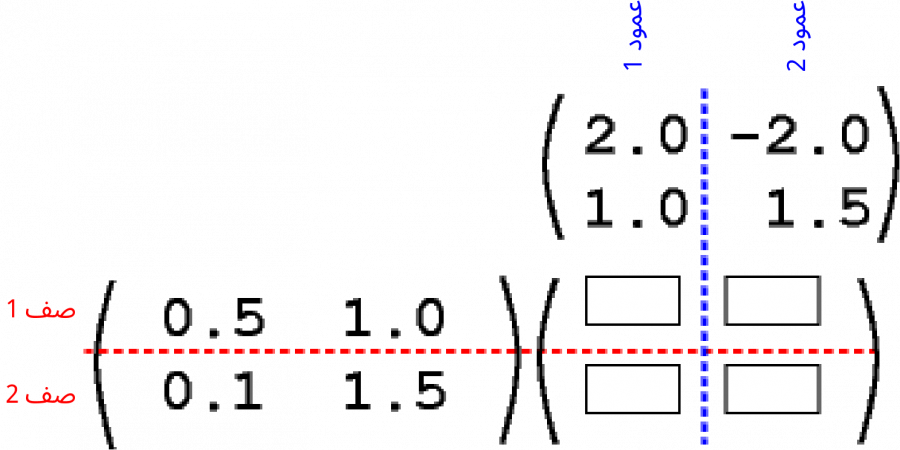
يوضّح الرسم البياني التالي مثلًا طريقةً أخرى لتصور عملية الضرب AB = C؛ إذ سنكتب المصفوفة A على يسار المصفوفة الناتجة C والمصفوفة B فوقها، ثم نرسم خطوطًا أفقية وأخرى عمودية لتقسيم المصفوفة C إلى خلايا؛ وسيؤدي ذلك تلقائيًا إلى تشكيل العدد الصحيح من الخلايا.
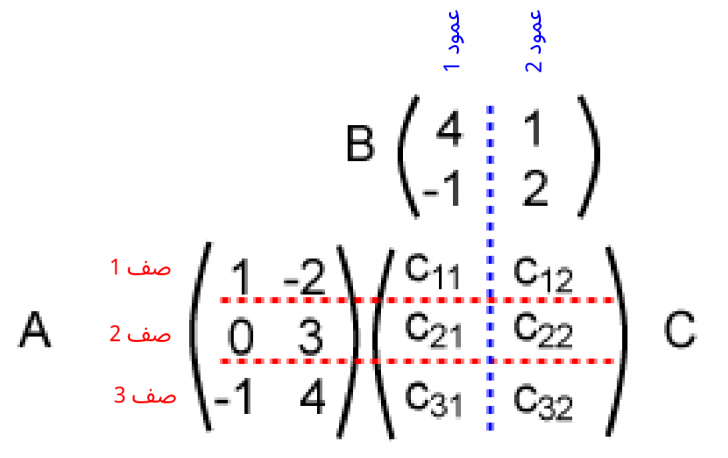
ينتج العدد الذي يجب وضعه في كل خلية من حاصل الجداء النقطي لصف المصفوفة A مع عمود المصفوفة B اللذين يتقاطعان عند هذه الخلية.
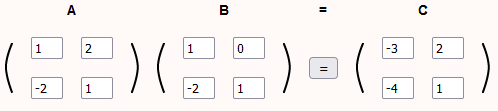
لنحسب الآن قيمة العنصرين c11 و c32 كما يلي:
c11 = 1×4 + -2×-1 = 6
c32 = -1×1 + 4×2 = 7
سنجرّب الآن حساب حاصل الجداء النقطي الخاص بكل خلية في الرسم البياني التالي:
وستكون المصفوفة الناتجة هي المصفوفة التالية:
عناصر المصفوفة هي أعداد حقيقية
يُعَد كل عنصر في المصفوفة مقدارًا سلميًا Scalar أي عددًا حقيقيًا.
لقد استخدمنا في أمثلتنا السابقة أعدادًا صحيحة حتى تكون العملية الحسابية سهلة، ولكن إليك مثال آخر مع قيم عشرية:
تشتمل معظم برامج جداول البيانات والآلات الحاسبة الإلكترونية العلمية على دالات رياضية خاصة بالمصفوفات؛ لكن من الأفضل محاولة إجراء الحسابات ذاتيًا عند التعلم من أجل استيعاب العملية.
اقتباس"من المهم التدرب على إجراء ضرب المصفوفات حتى يصبح الأمر بديهيًا لنا، كما يجب أن نكون قادرين لأجل ذلك على انتقاء صفٍ من المصفوفة A وعمودٍ من المصفوفة B مباشرةً؛ بحيث يُدمجان لإعطاء مدخل معين في المصفوفة AB". بن نوبل Ben Noble وجيمس دانيال James Daniel، من كتاب الجبر الخطي التطبيقي-النسخة الثالثة لدار النشر برنتيس هول عام 1988.
عملية ضرب المصفوفات ليست عملية تبديلية
لا تُعَد المساواة AB= BA صحيحةً دائمًا، فحتى إذا تمكنا من تشكيل هاتين العمليتين، فمن النادر أن تكون نتيجتهما متساويتين. لنحسب مثلًا عمليتي الضرب التاليتين:
| العملية | النتيجة |
|---|---|
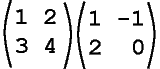
|
الناتج 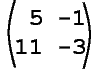
|
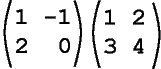
|
الناتج 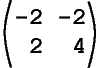
|
وهذا يوضّح أن AB ≠ BAبصورة عامة بالنسبة للمصفوفتين A و B، ولكن يمكن مثلًا:
A4×4 04×4 = 04×4 A4×4 = 04×4
المصفوفة 0 هي المصفوفة الصفرية ذات الأبعاد الصحيحة لجعل عملية الضرب ممكنة، وبالتالي يمكن أن تكون عملية الضرب عمليةً تبديليةً AB = BA بالنسبة لبعض المصفوفات؛ ولكن لا يمكننا تعميم هذه الخاصية على جميع المصفوفات.
تدريب عملي
لنوجد ناتج ضرب المصفوفتين التاليتين:
لنجرب أيضًا ضرب المصفوفتين التاليتين مثلًا:
استخراج عامل عددي من مصفوفة
ليكن c(AB) = (cA)B من أجل العدد الحقيقي c، علمًا أن أن c A يعني أن كل عنصر من عناصر المصفوفة A مضروب بالعدد c. سنوضّح هذه القاعدة في المثال التالي:
يمكننا تبسيط عملية ضرب المصفوفات في كثير من الأحيان من خلال استخراج عامل عددي من إحدى المصفوفات كما في المثال التالي:
عملية ضرب المصفوفات هي عملية تجميعية
لنضرب المصفوفتين الأوليتين، ثم نضرب النتيجة بالمصفوفة الثالثة كما يلي:
ولنبدأ الآن بالمصفوفتين الأخيرتين أولًا كما يلي:
وكما هو واضح، الإجابة النهائية هي نفسها بكلا الطريقتين، وهذا يوضّح أن عملية ضرب المصفوفات هي عملية تجميعية Associative:
(AB) C = A (BC)
يجب أن تكون الأبعاد الداخلية للمصفوفتين A و B نفسها، كما يجب أن تكون الأبعاد الداخلية للمصفوفتين B و C نفسها.
تُكتَب عملية ضرب ثلاث مصفوفات في العادة بالشكل الآتي: ABC. إذًا لنفترض مثلًا:
A5×5 B?×? C3×4 = D?×?
حيث تكون أبعاد المصفوفتين B و D كما يلي:
A5×5 B5×3 C3×4 = D5×4
خاصية توزيع ضرب المصفوفات في جمعها
تتعامل خاصية التوزيع مع تعبيرٍ يحتوي على كلٍّ من عمليتي ضرب وجمع المصفوفات؛ وسنتبع الخطوات التالية لذلك.
- أولًا، نجمع المصفوفتين كما يلي:
- ثانيًا، نضرب المصفوفتين:
- ثالثًا، نجري العملية مرةً أخرى بترتيب مختلف؛ إذ سنجري أولًا عملية ضرب المصفوفة اليسرى بكل من المصفوفتين الأخريين كما يلي:
- في الأخير، نجمع ناتج عمليتي الضرب السابقتين:
وكما نلاحظ، كلتا النتيجتين متماثلتان، مما يدل على أن ضرب المصفوفات توزيعيٌّ على جمعها:
A (B + C) = AB + AC
ويمكن القول أيضًا أن:
(X + Y) Z = XZ + YZ
ملاحظة: استخدمنا في معظم أمثلتنا أعدادًا صحيحة، ولكن لا يجب أن ننسى أن عناصر المصفوفة قد تكون أعددًا حقيقية أو متغيرات كما يلي:
ملخص بالقواعد الخاصة بعملية ضرب المصفوفات
سنذكر الآن قائمة بالقواعد الخاصة بعملية ضرب المصفوفات التي ناقشناها في هذا المقال، حيث تفترض كل قاعدة أنه يمكن ضرب المصفوفات؛ أي أن أبعادها مناسبة لعملية الضرب:
- يمكن تشكيل عملية ضرب المصفوفات في حال:
إذا كان AM×K BK×N = C، فإن C = CM×N
- ضرب المصفوفات ليس عملية تبديلية:
AB ≠ BA، إلّا في حالات ناردة
- ضرب المصفوفات هو عملية تجميعية:
A (BC) = (AB) C = ABC
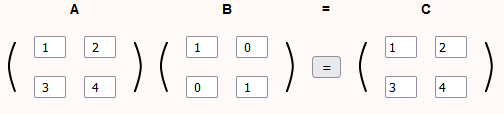
- استخراج المعامل العددي من المصفوفات:
a(AB) = (a A) B = a AB = A (a B)
- خاصية التوزيع على الجمع:
A ( B + C) = AB + AC
(A + B) C = AC + BC
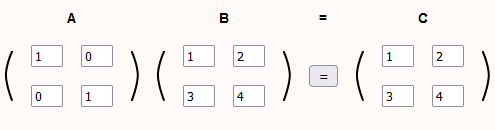
- الضرب بالمصفوفة الصفرية 0:
0A = 0
بهذا نكون قد وصلنا إلى نهاية هذا المقال التي تعرّفنا من خلاله على عملية ضرب المصفوفات وحسابها، وسنناقش في المقال التالي مزيدًا من خاصيات عملية ضرب المصفوفة بمصفوفة أخرى.
ترجمة -وبتصرُّف- للفصل Matrix-Matrix Multiplication من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.


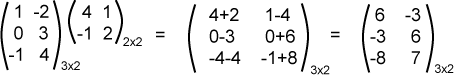
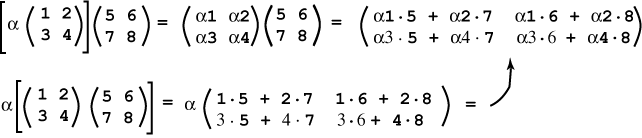
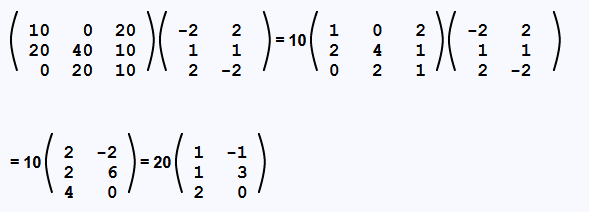




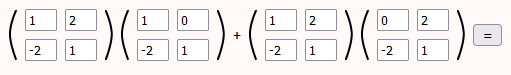

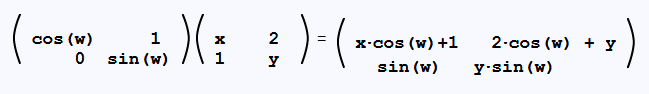








أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.