سنناقش في هذا المقال كيفية جداء الشعاع مععدد حقيقي، حيث تُسمَّى هذه العملية بتغيير الحجم Scaling، وكيفية استخدامها لبناء أشعة الوحدة Unit Vectors التي تُستخدَم لإظهار الاتجاه في الفضاء ثلاثي الأبعاد، وهي ضرورية للرسوميات الحاسوبية ثلاثية الأبعاد.
سنوضح في هذا المقال المواضيع التالية:
- تغيير حجم الشعاع Scaling وخاصياته.
- معامل تغيير الحجم Scalar.
- مساواة العناصر المتقابلة في جبر الأشعة.
- أشعة الوحدة.
- توحيد Normalizing الأشعة.
- منحى Orientation شعاع الوحدة.
- المتغيرات في المعادلات الشعاعية.
جداء الشعاع مع عدد حقيقي (تغيير حجم الشعاع Scaling)
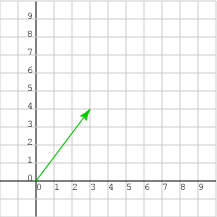
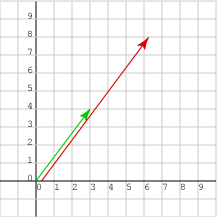
جرّب معرفة كيفية تعديل عناصر مصفوفة العمودية (3, 4)T بحيث يكون طول الشعاع الذي تمثله ضعف طوله الحالي ويبقى الشعاع يؤشّر إلى الاتجاه نفسه، إذ يمكنك التوصل إلى الإجابة الصحيحة بعناية باستخدام ما تعرفه مسبقًا، أو يمكنك التخمين ثم التحقق من صحة تخمينك كما يلي:
2 × (3, 4)T = (6, 😎T
لنرى إن كان تخمينك صحيحًا كما يلي:
- (الطول الجديد)2 = 62 + 82 = 22 32 + 22 42 = 22 (32 + 42) = 22 × (الطول القديم)2.
- إذًا بأخذ الجذر للطرفين: (الطول الجديد) = 2 × (الطول القديم)
- ويكون الاتجاه نفسه باستخدام المثلثات المتشابهة، أو يمكنك ملاحظة أن:
الاتجاه الجديد = arc tan( 8/6 ) = arc tan( 4/3 ) = الاتجاه القديم
وبالتالي يبدو تخمينك صحيحًا.
ملاحظة: يُطلَق على العدد الحقيقي أحيانًا اسم معامل تغيير الحجم (مقدار سلمي) Scalar عند الحديث عن الأشعة.
تعني عملية تغيير حجم Scaling الشعاع الهندسي إبقاءَ منحاه Orientation كما هو مع تغيير طوله باستخدام معامل تغيير حجم، إذ تشبه هذه العملية تغيير حجم الصورة، حيث تتوسّع أو تتقلّص الكائنات مع بقاء اتجاهاتها كما كانت سابقًا.
إذا كان الشعاع مُمثَّلًا بمصفوفة عمودية (x, y)T، فسيؤدي تغيير حجمه وفق عدد معين إلى جداء كل عنصر فيها بهذا العدد كما يلي:
a(x, y)T = (ax, ay)T
ينطبق ذلك أيضًا على الأشعة ثلاثية الأبعاد، فإذا مثّلنا الشعاع v بالمصفوفة العمودية (x, y, z)T، فسيكون تمثيل av بالمصفوفة العمودية (ax, ay, az)T.
أوجد ناتج 0.5×(36.4, -18.9)T:
0.5×(36.4, -18.9)T = (0.5×36.4, 0.5× -18.9)T = ( 18.2, -9.45)T
بعض خاصيات عملية تغيير حجم شعاع
هناك العديد من خاصيات تغيير حجم الشعاع التي سنوضّحها فيما يلي.
الشعاع الذي تغير حجمه هو شعاع أيضا
إذا كان v شعاعًا، فإن:
- -1 v = -v
- 0 v = 0
لاحظ أنه يجب توخي الدقة في العبارتين السابقتين، حيث:
- -1 v = -v: عدد حقيقي * شعاع = شعاع
- 0 v = 0: عدد حقيقي * شعاع = شعاع
نتيجة تغيير حجم شعاع هي شعاع أيضًا، ولاحظ أن 0 بالخط العريض هو شعاع تمثله المصفوفة العمودية (0,0,0)T، وليس العدد الحقيقي صفر.
التعابير ذات الأنواع المختلطة
أوجد ناتج 2 + 4( 3, 2, 5)T:
لا يُعَد هذا التعبير صحيحًا، إذ لا يوجد معامل جمع + يطبّق العملية: عدد حقيقي + شعاع
لذا من المفيد استخدام الأقواس لإظهار ما تعنيه بالضبط في التعابير التي تحتوي على أنواع ومعاملات مختلطة كما يلي:
(2 + 1)(3, -5)T + 4(1, 2)T
يمثّل المعامل + الأول عملية جمع لأعداد حقيقية (مقادير سلمية)، ويمثّل المعامل + الثاني عملية جمع لمصفوفات عمودية، لذا يجب تنفيذ العمليات كما يلي:
(2 + 1)(3, -5)T + 4(1, 2)T = 3(3, -5)T + 4(1, 2)T = (3×3, 3× -5)T + (4×1, 4×2)T = (9, -15)T + (4, 😎T = (13, -7)T
لا يُعَد تطبيق ذلك سيئًا كما يبدو، فما عليك إلّا تتبّع كل معامل وأنواع معامَلاته ونوع نتيجته.
لنوجد الآن ناتج -1 (1, 2, -3)T - (2 + 1)(1, 0, 1)T:
-1 (1, 2, -3)T - (2 + 1)(1, 0, 1)T = ( -1, -2, 3)T - 3(1, 0, 1)T = ( -1, -2, 3)T + (-3, 0, -3)T = (-4, -2, 0 )T
جبر الأشعة
إذا كان هناك عنصر مجهول أو اثنان في التعبير الذي يحتوي أنواع عمليات مختلطة، فيمكنك استخدام الجبر بالطريقة المعتادة للحل، ولكن كن حذرًا من أنّ كل خطوة تطبّقها تعطي تعبيرًا صالحًا. حل ما يلي مثلًا من أجل a و y:
a(1, y)T + 2(0, 5 )T = (2, 20)T
قد تقول أنه لا يمكن ذلك بسبب وجود مجهولين (a و y) مع معادلة واحدة فقط، ولكن:
a(1, y)T + 2(0, 5)T = (2, 20)T
(a, ay)T + (0, 10)T = (2, 20)T
(a, ay+10)T = (2, 20)T
يجب أن تكون العناصر المتقابلة متساوية، لذا:
a = 2
ay + 10 = 20
2y = 10
y = 5
تُعَد هذه الخدعة شائعة وتسمى مساواة العناصر المتقابلة Equating Corresponding Elements.
مساواة العناصر المتقابلة
لنوجد قيمة x و y فيما يلي:
4( -1, y)T + 2( 3x, 10)T = (8, 24)T
4( -1, y)T + 2( 3x, 10)T = (8, 24)T ( -4, 4y)T + ( 6x, 20)T = (8, 24)T (6x-4, 4y+20)T = (8, 24)T
6x-4 = 8 4y+20 = 24
6x = 12 x = 2
4y = 4 y = 1
تعني الإشارةُ "=" في المعادلة الأصلية معادلةً شعاعية، بينما تؤدي مساواة العناصر المتقابلة إلى الحصول على معادلتين، حيث تعني الإشارةُ "=" معادلة عددية أو معادلة أعداد حقيقية.
تتغير معادلة المصفوفات العمودية إلى عدة معادلات عددية باستخدام مساواة العناصر المتقابلة، حيث يكون لكل بُعد من المصفوفة العمودية معادلة واحدة، ويمكن بعد ذلك حل المعادلات العددية لإيجاد قيمة المجهول في بعض الأحيان وليس دائمًا.
إليك مثلًا حالة لا تنجح فيها هذه الطريقة:
أوجد قيمة x و y :
4(x, 5)T + 2(y, 1)T = 2(12, 11)T
قد يبدو كل شيء جيدًا، ولكن يكشف تطبيق بعض الخطوات عن وجود مشكلة كما يلي:
4( x, 5)T + 2( y, 1)T = 2(12, 11)T
(4x, 20)T + (2y, 2)T = (24, 22)T
(4x+2y, 22 )T = (24, 22)T
4x + 2y = 24
22 = 22
لا تحتوي المعادلتان العدديتان اللتان تحصل عليهما من خلال مساواة العناصر المتقابلة على معلومات كافية للمتابعة.
لنوجِد الآن قيمة a و x :
a( -1, 5 )T + 2( 3x, 10 )T = ( 8, 25 )T
يمكن أن نخمن أنه يمكننا إيجاد قيمة a و x كما يلي:
a( -1, 5 )T + 2( 3x, 10 )T = ( 8, 25 )T ( -a, 5a)T + ( 6x, 20 )T = ( 8, 25 )T ( 6x-a, 5a+20 )T = ( 8, 25 )T
ولنستخدم الآن مساواة العناصر المتقابلة:
6x-a = 8 5a+20 = 25 5a = 5 a = 1 6x-1 = 8 6x = 9 x = 9/6 x = 3/2
تغيير حجم شعاع باستخدام قيم أصغر من واحد
نعلم من تعريف عملية تغيير حجم شعاع أنه:
a( x, y )T = ( ax, ay )T
فلا بأس إن كان a أصغر من واحد، فمثلًا:
0.5( x, y )T = ( 0.5x, 0.5y )T
يمكن كتابة ذلك في بعض الأحيان على النحو التالي:
شعاع الوحدة
اقتباستذكير: ما هو طول الشعاع (1,0)T؟ طوله يساوي 1.0.
يبلغ طول الشعاع 1 لأنه محاذٍ للمحور x (في إطار الإحداثيات الحالي)، فالعنصر الوحيد غير الصفري هو 1.0 عند تمثيله بمصفوفة عمودية، ولكن يمكن أيضًا أن يساوي طول الأشعة غير المحاذية لأيّ محور واحدًا، وبالتالي فإن شعاع الوحدة Unit Vector هو شعاع طوله 1.
هل يمثل (1, 1, 1)T شعاع وحدة؟ لا، لا يمثل شعاع وحدة لأن طوله لا يساوي 1:
√( 12 + 12 + 12 ) = √3 = 1.7320508
إنشاء أشعة الوحدة
يبلغ طول أشعة الوحدة 1، وإذا كان لديك شعاع معين v، فيمكنك استخدامه لإنشاء شعاع وحدة، وتسمى هذه العملية بتوحيد الأشعة Normalizing التي تُطبَّق كما يلي:
- احسب طول الشعاع v وهو | v |.
- غيّر حجم الشعاع v من خلال تقسيمه على طوله: .v / | v |
تُكتَب هذه العملية في كثير من الأحيان بالصيغة التالية (يعني الحرف "u" المنخفض "شعاعَ وحدة Unit Vector"):
vu = v / | v |
إذا كان v = (x, y, z)T، فإن:
vu = v / | v | = ( x /| v |, y /| v |, z /| v | )T
تستخدم بعض المصادر ترميزًا مختلفًا لذلك، حيث يُستخدَم رمز "القبعة" لأشعة الوحدة î ولكنه لا يظهر جيدًا في المتصفحات، ويسمَّى شعاع الوحدة أحيانًا بالشعاع "المُوحَّد Normalized".
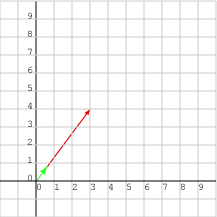
جرب توحيد الشعاع (3, 4)T كما يلي:
الشعاع هو الوتر في المثلث القائم 3-4-5، وبالتالي فإن طوله هو 5، وشعاع الوحدة هو:
1/5 × (3,4)T = (3/5, 4/5)T = (0.6, 0.8)T
اتجاه شعاع الوحدة
تؤدي عملية تغيير الحجم إلى تغيير طول الشعاع دون تغيير اتجاهه، حيث إذا كان vu هو شعاع الوحدة المقابل للشعاع v، فإن الشعاعين vu و v لهما المنحى نفسه.
قد يبدو ذلك مفهومًا، ولكن لنوضّحه أكثر:
- ابدأ بالشعاع v = (3, 4)T.
- أنشئ شعاع الوحدة vu = (3/5, 4/5)T.
- اتجاه الشعاع v هو arc tan( 4/3 ).
- اتجاه vu هو:
arc tan( (4/5) / (3/5) ) = arc tan( (4/5) × (5/3) ) = arc tan( 4/3 )
يمكننا إنشاء شعاع وحدة له اتجاه الشعاع w = (4, 6)T نفسه مثلًا كما يلي:
| w | = √(16 + 36) = √52
wu = (4, 6)T / ( √52)
ولنتأكد الآن من صحة الإجابة:
| wu |T = (4T + 6T) / ( √52)T = (16 + 36)/52 = 52/52 =1.0
| wu | = 1.0
يؤشّر شعاع الوحدة المتشكّل من شعاع ثلاثي الأبعاد إلى اتجاه الشعاع الأصلي نفسه أيضًا، إذًا لنجرّب مثلًا توحيد الشعاع g = (-3, 4, -1)T:
| g | = √(9 + 16 + 1 ) = √26
gu = (-3, 4, -1)T / (√26)
الاتجاه المعاكس
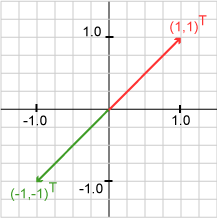
يمثل (1, 1)T / (√2) شعاعَ وحدة له منحى مقداره 45 درجة، وطوله √( 12/2 + 12/2 ) = 1، وزاويته مقدارها arctan(1/1) = 45 درجة، ولكن يمكنك إنشاء شعاع وحدة يؤشّر في الاتجاه المعاكس لهذا الشعاع من خلال أخذ معاكس كل مكوّن من مكوناته كما يلي:
-( 1, 1)T / (√2) = (-1, -1)T / (√2)
تدريب:
أنشئ شعاع وحدة يؤشّر إلى الاتجاه المعاكس للشعاع (3, 0, 2)T:
- طول الشعاع = √(9+4) = √13
- شعاع الوحدة في الاتجاه الأول = (3, 0, 2)T / ( √13)
- شعاع الوحدة في الاتجاه المعاكس = ( -3, 0, -2)T / ( √13)
بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على مفهوم تغيير حجم الأشعة وشعاع الوحدة، وسنناقش في المقال التالي الجداء النقطي Dot Product لشعاعين في التصاميم ثلاثية الأبعاد.
ترجمة -وبتصرُّف- للفصل Scaling and Unit Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.


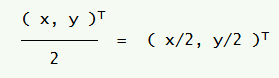











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.