الأشعة تطبيق الجداء النقطي Dot Product على الأشعة في التصاميم 3D

سنتعّرف في هذا المقال على المواضيع التالية:

• الأسماء المختلفة التي يُعرَف بها الجداء النقطي.
• تعريف الجداء النقطي للأشعة الهندسية.
• الخاصية التبديلية للجداء النقطي للأشعة.
• جيب تمام Cosine الزاوية.
• الجداء النقطي للأشعة المتعامدة.
• الجداء النقطي وطول الشعاع.
• خاصيات الجداء النقطي للأشعة.
• الجداء النقطي للمصفوفات العمودية ثنائية الأبعاد.
• الخاصية التبديلية للجداء النقطي للمصفوفات العمودية.
• الجداء النقطي للمصفوفات العمودية ثلاثية الأبعاد.
• الجداء النقطي للمصفوفة العمودية مع نفسها.
• خاصية توزيع الجداء النقطي للمصفوفات العمودية.

تعرّفنا حتى الآن على العمليات التالية:

‪| جمع شعاعين | شعاع + شعاع | = | شعاع |

| طرح شعاعين | شعاع - شعاع | = | شعاع |

| الفرق بين نقطتين | نقطة - نقطة | = | شعاع |

| تغيير حجم شعاع (ضرب شعاع بعدد حقيقي) | عدد حقيقي * شعاع | = | شعاع |

سنناقش في هذا المقال الجداء النقطي Dot Product الذي يأخذ شعاعين بوصفهما معاملَين وينتج عنه عدد حقيقي بوصفه الخرج. يسمّى الجداء النقطي في بعض الأحيان بالجداء الداخلي Inner Product، ويسمّى أحيانًا أخرى بالجداء السلمي Scalar Product، والذي لا ينبغي الخلط بينه وبين العملية التي تسمى تغيير حجم الشعاع Scaling (ضرب الشعاع بعدد حقيقي).

| الجداء النقطي | شعاع . شعاع | = | عدد حقيقي Scalar (مقدار سلمي) |

ملاحظة: يُسمى الجداء النقطي أحيانًا بالجداء السلمي، لأنه يأخذ شعاعين وينتج عنه عدد حقيقي Scalar (مقدار سلمي).

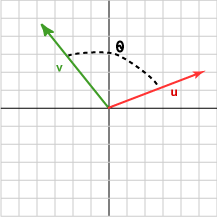
الزاوية بين شعاعين

الزاوية بين الشعاعين u و v هي الزاوية θ التي تكون:

0‪ <= θ <= 180 درجة

ويكون ذلك صحيحًا لكل من الفضاء ثنائي الأبعاد وثلاثي الأبعاد، فهذه الزاوية هي أصغر زاوية يمكن أن يدورها أحد الأشعة حتى يحاذي الشعاع الآخر. ولكن إذا كان هناك شعاعان يؤشّران إلى اتجاهين متعاكسين، فستكون الزاوية بينهما تساوي 180 درجة (أو π راديان).

الجداء النقطي

يكون الجداء النقطي للشعاعين u و v بالنسبة للأشعة الهندسية في الفضاء ثنائي أو ثلاثي الأبعاد هو:

u · v = | u | | v | cos θ‪

يُرمَز للجداء النقطي بنقطة بين الشعاعين، ولكن لا تظهِر العديد من المتصفحات النقطة بصورة واضحة لسوء الحظ، إذ قد ترى نقطة صغيرة جدًا أو شريطًا أسود صغيرًا، ويمثّل الرمز θ الزاوية بين هذين الشعاعين.

اقتباس

لا تكتب الشعاعين بجانب بعضهما بعضًا بهذه الطريقة: uv عندما تريد استخدام الجداء النقطي، بل ضع دائمًا نقطة بينهما: u · v.

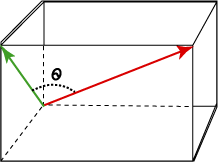
يقع الشعاعان في مستوٍ واحد في الفضاء ثنائي الأبعاد، وبالتالي من السهل تصوّر الزاوية بينهما، بينما يقع الشعاعان في الفضاء ثلاثي الأبعاد في مستوٍ مُضمَّن في هذا الفضاء إلا في الحالة التي يؤشّر فيها الشعاعان إلى الاتجاه نفسه.

تكون الزاوية بين الشعاعين صفرًا عندما يؤشّران إلى الاتجاه نفسه وبالتالي:

u · v = | u | | v | cos 0 = | u | | v | 1 = | u | | v |‪

بما أن ‎-1 <= cos θ <= +1 فستكون قيمة نتيجة الجداء النقطي بين القيمتين ‎-| u | | v |‎ و ‎+| u | | v |‎ اعتمادًا على الزاوية بين الشعاعين، بينما تكون الزاوية بين الشعاعان 180 درجة وتكون قيمة نتيجة الجداء النقطي هي ‎-| u | | v |‎ عندما يؤشّر هذان الشعاعان إلى اتجاهين متعاكسين.

الخاصية التبديلية Commutative للجداء النقطي

إذا كان ‎u · v = | u | | v | cos θ، فإن v · u:

v · u = | v | | u | cos θ = | u | | v | cos θ = u · v‪‪‪‪

تُعَد عملية الجداء النقطي عملية تبديلية، إذ لا يحدِث ترتيب المعاملات أيّ فرق:

‪u · v = v · u‪

cنوعان مختلفان من الأصفار في المعادلة التالية، إذ تكون معامَلات عملية الجداء النقطي شعاعَين، ويكون خرج العملية قيمة سلمية (عددًا حقيقيًا):

0‪ · 0 = 0‪

يمكن إيجاد a (u · v)‎ حيث "a" عدد حقيقي كما يلي:

a (u · v) = a | u | | v | cos θ‪‪

نعيد ترتيب الصيغة السابقة، فينتج:

‪= | a u | | v | cos θ = (a u) · v = u · (a v)

جيب تمام Cosine الزاوية 90 درجة

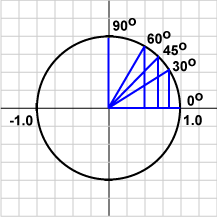
قد تكون كيفية عمل دالة جيب التمام Cosine غامضةً إلى حدٍ، لذا تخيّل دائرة الوحدة مع إسقاط نصف قطرها على المحور x كما في الشكل السابق الذي ينتج عنه ما يلي:

• جيب تمام الزاوية 0 درجة = 1.0
• جيب تمام الزاوية 30 درجة = 0.866
• جيب تمام الزاوية 45 درجة = 0.707
• جيب تمام الزاوية 60 درجة = 0.500
• جيب تمام الزاوية 90 درجة = 0.0

وتذكّر أن:

u · v = | u | | v | cos θ‪‪‪

الجداء النقطي للأشعة المتعامدة Orthogonal

لنفترض أن لدينا شعاعين بينهما زاوية مقدارها 90 درجة، أي أنهما شعاعان متعامدان. هنا يمكن إيجاد جدائهما النقطي كما يلي:

u · v = | u | | v | cos 90° = | u | | v | 0.0 = 0.0‪

وبالتالي نستنتج أن الجداء النقطي للأشعة المتعامدة هو صفر، ويمكن تطبيق هذه الحقيقة على الأشعة في جميع الأبعاد.

نعني بالشعاعين المتعامدين أن بينهما زاوية مقدارها 90 درجة، ويُعَد الشعاع الصفري متعامدًا مع جميع الأشعة الأخرى، حيث أن ‎0 · v = 0.0 لجميع الأشعة v .

كشف التعامد وحساب الطول

لنفترض أن الشعاعين s و t ناتج الجداء النقطي لهما يساوي صفر، إذًا:

• ماذا يمكنك أن تقول عن المنحى النسبي Relative Orientation للشعاعين s و t؟ الشعاعان s و t متعامدان.
• ماذا يمكنك أن تقول عن طولي الشعاعين s و t؟ لا يمكنك قول أيّ شيء ممّا تعرفه عن الجداء النقطي.

إذا كان لدينا شعاعان متعامدان فيما بينهما، فسيكون جداؤها النقطي صفرًا بغض النظر عن أطوالهما، إذ يكتشف الجداء النقطي التعامد بغض النظر عن أطوال الأشعة.

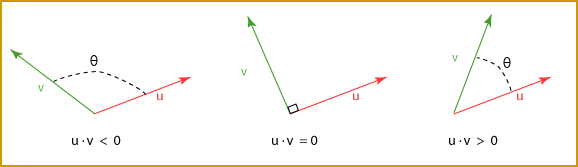
ملاحظة: تعتمد إشارة الجداء النقطي لشعاعين u و v على ما إذا كانت الزاوية بينهما حادة أم منفرجة، فإذا كانت قيمة الجداء النقطي صفرًا، فستكون الأشعة متعامدة.

لنطّلع الآن على الجداء النقطي للشعاع مع نفسه:

v · v = | v | | v | cos 0 = | v | | v | 1.0 = | v |^2‪‪

وبالتالي فإن الجداء النقطي للشعاع مع نفسه يساوي مربع طوله.

‪| ‪v | = √(v · v)‪

يحسب الجداءُ النقطي الطولَ باستخدام الصيغة السابقة، وبالتالي يُعَد الجداء النقطي مفيدًا بما أن خاصيتي الشعاع هما الطول والمنحى Orientation، ولكن يمكن أن تتساءل عن إمكانية أن يكون قيمة ‎| ‎v | = √(v · v)‎ سالبة أو صفرًا. حسنًا، لا يمكن أن تكون سالبة، لأن الطول يكون دائمًا صفرًا أو قيمة موجبة، ويكون المقدار ‎| ‎v | = √(v · v)‎ صفرًا عندما يكون الشعاع v هو الشعاع الصفري.

خاصيات الجداء النقطي

سنسرد فيما يلي قائمة بخاصيات الجداء النقطي وهي:

1. ‎u · v = | u | | v | cos θ: حاصل الجداء النقطي لشعاعين
2. u · v = v · u: الخاصية التبديلية للجداء النقطي لشعاعين
3. ‎u · v = 0 : حيث u و v شعاعين متعامدين
4. 0 · 0 = 0
5. ‎| v |² = v · v‎
6. a (u·v) = (a u) · v‎
7. ‎u . (v + w ) = (u . v) + (u . w)‎
8. (v + w ) . u = (v . u) + (w . u) = (u . v) + (u . w)
9. ‎(au + bv) · w = (au) · w + (bv) · w‎: حيث a و b قيم سلمية (أعداد حقيقية)
10. ‎0 . u = 0: حيث 0 (بالخط العريض) هو الشعاع الصفري، و 0 هو عدد‫ حقيقي (مقدار سلمي)

ما هو ناتج جداء ‎u · v · w‎؟

ليس للجداء u · v · w معنىً، فإذا كان ‎u · v = a (حيث a عدد حقيقي)، فإن a · w‎ لا معنى له، وإذا كان ‎v · w = b (حيث b عدد حقيقي)، فإن ‎u · b لا معنى له، وليس للتعبير الأصلي أيّ معنًى في كلتا الحالتين.

إذًا ما هو ناتج 0‎ · u‎؟

• إذا كان "0" (بخط عادي غير عريض) عددًا حقيقيًا، فإن هذه العملية لا معنى لها.
• إذا كان "0" (بخط عريض) شعاعًا صفريًا، فالنتيجة هي 0 (عدد حقيقي أو مقدار سلمي).

الجداء النقطي للمصفوفات العمودية

يمكن استخدام الجداء النقطي أيضًا مع المصفوفات العمودية. ليكن لدينا مثلًا المصفوفتان العموديتان التاليتان:

a = ( a₁, a₂ )^T‪

b = ( b₁, b₂ )^T

فيمكننا تعريف الجداء النقطي لهما على النحو التالي:

a · b = a₁b₁ + a₂b₂

حيث نضرب العناصر المتقابلة لكل مصفوفة عمودية، ثم نجمع النواتج، وستكون نتيجة الجداء النقطي قيمة عددية (سلمية).

ملاحظة: نكتب الجداء النقطي للمصفوفات العمودية في بعض الأحيان على النحو التالي: a^T b (مع التعريف نفسه)، وسنوضّح لاحقًا هذه الصيغة الغريبة عند مناقشة ضرب المصفوفات.

أوجد ناتج الجداء النقطي للمصفوفتين العموديتين التاليتين:

a = ( 1, 2 )^T

b = ( 3, 4 )^T

والناتج هو:

a · b = 1*3 + 2*4 = 3 + 8 = 11

ولنوجد الآن حاصل جداء b · a كما يلي:

b · a = 3*1 + 4*2 = 1*3 + 2*4 = a · b

خاصيات الجداء النقطي للمصفوفات العمودية

يمتلك الجداء النقطي للمصفوفات العمودية الخاصيات نفسها للجداء النقطي للأشعة، والتي سنوضحها في الفقرات التالية، ولكن لنأخذ أولًا مثالًا لنتعرّف من خلاله على الجداء النقطي للمصفوفات العمودية.

لنفترض أن لدينا المصفوفتين العموديتين التاليتين:

p = ( -2, 5 )^T

q = ( 3, -1 )^T

وسيكون الجداء النقطي لهما هو:

p · q = (-2)*3 + 5*( -1) = -6 + -5 = -11‪

وإليك مثال آخر أكثر واقعية:

لنفترض أن لدينا المصفوفتين العموديتين التاليتين:

s = ( 1.082, -3.224 )^T

t = ( 2.381, 7.009 )^T

وسيكون الجداء النقطي لهما هو:

s · t = 1.082*2.381 + -3.224*7.009 = 2.576242 + -22.597016 = -20.020774‪

لاحظ أن الجداء النقطي يأخذ معاملين هما مصفوفتان عموديتان وينتج عنه قيمة عددية (سلّمية) واحدة في جميع الحالات.

الخاصية التبديلية للجداء النقطي للمصفوفات العمودية

لنوجد مثلًا الجداء النقطي للمصفوفتين ‎( -1, 3)^T‎ و ‎( 2, 4 )^T‎، ثم الجداء النقطي للمصفوفتين ‎( 2, 4 )^T‎ و ‎( -1, 3)^T‎ كما يلي:

‪( -1, 3)^T · ( 2, 4 )^T = -12 + 3*4 = -2 + 12 = 10‪

‪( 2, 4 )^T · ( -1, 3)^T = 2*(-1) + 4*3 = -2 + 12 = 10

وبالتالي نستنتج أن الجداء النقطي للمصفوفات العمودية هو عملية تبديلية:

a · b = b · a

لا يشكّل ترتيب المعاملات أيّ فرق كما هو الحال مع الجداء النقطي للأشعة، حيث يمكننا كتابة تعريف الجداء النقطي للمصفوفتين a و b في كلا الترتيبين كما يلي:

a · b = ( a₁, a₂ )^T · ( b₁, b₂ )^T = a₁b₁ + a₂b_2‪

b · a = ( b₁, b₂ )^T · ( a₁, a₂ )^T = b₁a₁ + b₂a₂ = a₁b₁ + a₂b_2‪

لاحظ أن الأشياء الموجودة بعد إِشارة المساواة "=" الأخيرة هي نفسها في الحالتين.

الجداء النقطي لأنواع المعاملات المختلطة

لنفترض أننا نريد إيجاد الجداء النقطي للمصفوفات العمودية a و b و c:

a · b · c

لكن هذه العملية لا معنى له، إذ ينتج عن الجداء النقطي لشعاعين (أو مصفوفتين عموديتين) عدد حقيقي، ولا يوجد شيء اسمه الجداء النقطي لعدد حقيقي وشعاع (أو مصفوفة عمودية)، فلا معنى للعملية التالية:

a · b · c‪ = عدد حقيقي · c

أو للعملية التالية:

a · b · c = a‪ · عدد حقيقي

لذا يجب عليك أن تتابع أنواع المعاملات والنتائج عند التعامل مع الجداء النقطي.

لكن العملية التالية لها معنًى (لاحظ أنه لا توجد نقطة بين العدد 2 والشعاع الذي يليه، وهذا يمثّل عملية تغيير الحجم أو ضرب الشعاع بعدد حقيقي Scaling، وليس الجداء النقطي):

2‪( -1, 2)^T · ( 4, 1 )^T = ( -2, 4)^T · ( 4, 1 )^T = -2*4 + 4*1 = -8 + 4 = -4

الجداء النقطي في فضاء ثلاثي الأبعاد

نعرّف الجداء النقطي لمصفوفات عمودية ثلاثية الأبعاد كما يلي، حيث نضرب العناصر المتقابلة في المصفوفتين ثم نجمع النواتج.

ليكن لدينا المصفوفتان العموديتان التاليتان:

a = ( a₁, a₂, a₃ )^T

b = ( b₁, b₂, b₃ )^T

فيمكننا تعريف الجداء النقطي لهما على النحو التالي:

a · b = a₁b₁ + a₂b₂ + a₃b₃

لكن يجب أن تحتوي المصفوفتان العموديتان على عدد العناصر نفسه كما في المثالين التاليين:

‪(1, 2, 3)^T · (6, 7, 😎^T = 1*6 + 2*7 + 3*8 = 44

‪( -1, 2, -3)^T · (1, -2, 3)^T = (-1)(1) + (2)(-2) + (-3)(3) = -1 + -4 + -9 = -14‪

ولا مانع من وجود بعض المتغيرات كعناصر للأشعة كما يلي:

‪(1, 2, 3)^T · (x, y, z)^T = x + 2y + 3z‪‪

الجداء النقطي مع شعاع صفري

جرّب إيجاد ناتج الجداء النقطي للمصفوفتين ‎( 4, 0, -3)^T‎ و ‎(0, -2, 0)^T‎ كما يلي:

‪‪( 4, 0, -3)^T · (0, -2, 0)^T = 4*0 + 0*(-2) + (-3)*0 = 0+0+0 = 0

لاحظ أن قيمة طول كل شعاع في الجداء النقطي السابق أكبر من الصفر، ولكن قيمة حاصل الجداء النقطي صفر.

إليك مثال آخر:

v(0, 0, 0)^T · (-2.3, 89.22, 0)^T = 0(-2.3) + 0(89.22) + 0(0) = 0‪

ولا يُعَد ذلك مفاجأة، إذ رأينا الخاصية التالية نفسها مع الأشعة الهندسية:

0‪ · a = 0‪

لاحظ أن 0 الأول هو المصفوفة العمودية الصفرية، والصفر الأخير هو العدد الحقيقي صفر، ويمكن أيضًا كتابة ما يلي:

0‪ · 0 = ‪0

تعني المصفوفة العمودية الصفرية في كل من هذه المعادلات مصفوفة عمودية لها بُعد المصفوفة العمودية الأخرى نفسه، وكل عنصر فيها هو العدد الحقيقي صفر.

ناتج الجداء النقطي هو جميع القيم الحقيقية الممكنة

أوجد ناتج الجداء النقطي للمصفوفتين ‎(-2, 5, -6)^T‎ و ‎( 1, 2, 3)^T‎:

v(-2, 5, -6)^T · ( 1, 2, 3)^T = (-2)*1 + 5*2 + (-6)*3 = -2 + 10 -18 = -10

لاحظ أن الجواب هو عدد حقيقي سالب، إذ ينتج عن الجداء النقطي جميع أنواع القيم الحقيقية: سالبة وصفر وموجبة، ولكن هناك شيء مهم يحدث عند إجراء عملية الجداء النقطي للشعاع مع نفسه، وهذا ما سنوضّحه في الفقرة التالية.

ناتج الجداء النقطي للمصفوفة العمودية مع نفسها هو قيمة موجبة أو صفرية

لنوجد مثلًا الجداء النقطي للشعاع ‎(1, -3)^T‎ مع نفسه كما يلي:

v(1, -3)^T · (1, -3)^T = (1)(1) + (-3)(-3) = 1 + 9 = 10

يكون ناتج الجداء النقطي للمصفوفة العمودية مع نفسها موجبًا دائمًا كما هو الحال مع الأشعة.

‪(x, y, z)^T · (x, y, z)^T = x² + y² + z² = قيمة موجبة أو صفرية

سيكون مربع x و y و z صفرًا أو أكبر من الصفر بغض النظر عن قيمها، وبالتالي سيكون المجموع صفرًا أو أكبر من الصفر، ولكن المرة الوحيدة التي يكون فيها مربع العدد الحقيقي صفرًا هي عندما يكون هذا العدد الحقيقي صفرًا، لذا فالمرة الوحيدة التي يكون فيها حاصل الجداء النقطي لمصفوفة عمودية مع نفسها صفرًا هي عندما تكون المصفوفة العمودية مصفوفة صفرية.

ليكن g شعاعًا ثلاثيّ الأبعاد، فأوجد قيم عناصر هذا الشعاع من خلال حل المعادلة التالية:

g · g = 0‪‪

نلاحظ أنه يجب أن يكون كل عنصر من عناصر الشعاع g صفرًا من خلال المناقشة السابقة، لذا:

g = 0 = (0, 0, 0)^T‪

قابلية توزيع الجداء النقطي على الجمع

يمكن توزيع الجداء النقطي على عملية الجمع كما يلي:

a · (b + c) = a · b + a · c‪

يبدو هذا جيدًا، ولكن كن حذرًا في تحديد ما تعنيه إشارة "+" على جانبي إشارة المساواة "=".

1. تمثّل إشارة "+" في الجانب الأيسر من المعادلة عملية جمع الأشعة.
2. تمثّل إشارة "+" في الجانب الأيمن من المعادلة عملية جمع الأعداد الحقيقية.

من السهل إلى حدٍ ما إثبات أن خاصية التوزيع صحيحة، إذًا لنوضّح هذه الخاصية باستخدام المصفوفات العمودية ثلاثية الأبعاد، بالرغم من أنه يمكن استخدامها مع أيّ بُعد. ويمثّل كلا طرفي المعادلة عددًا حقيقيًا، لذا يجب التحقق من أن هذين الطرفين يمثلان العدد الحقيقي نفسه.

إذًا لنبرهن أن ‎a · (b + c) = a · b + a · c‎.

ليكن لدينا المصفوفات العمودية التالية:

a = (f, g, h)^T

b = (r, s, t)^T

c = (x, y, z)^T

نبدأ بالطرف الأيسر:

a · (b + c) = a · ( r+x, s+y, t+z )^T = f(r+x) + g(s+y) + h(t+z) = fr + fx + gs + gy + ht + hz‪

ثم بالطرف الأيمن:

a · b + a · c = (fr + gs + ht) + (fx + gy + hz) = fr + fx + gs + gy + ht + hz‪

ينتج لدينا أن طرفي المعادلة يمثلان العدد الحقيقي نفسه، ويمكن إجراء الشيء نفسه مع الأشعة بجميع الأبعاد، وبالتالي فإن خاصية التوزيع تكون صحيحة مع جميع الأبعاد.

تدريب عملي

أوجد ناتج الجداء النقطي التالي:

v( -2, 1, 2)^T · ( (3, -1, 4)^T + ( -2, 1, -2)^T )

قد يكون من الأسهل عدم إعادة ترتيب التعبير، بل يُفضَّل إجراء عملية جمع الأشعة أولًا كما يلي:

‪( -2, 1, 2)^T · ( (3, -1, 4)^T + ( -2, 1, -2)^T ) = ( -2, 1, 2)^T · (1, 0, 2)^T = -2*1 + 1*0 + 2*2 = -2 + 4 = 2

وتكون إعادة ترتيب التعبير أسهل في أحيان أخرى كما في المثال التالي، حيث يكون من الأسهل إجراء عملية الجداء النقطي أولًا:

‪( -2, 0, 2)^T · ( (1, -1, 1)^T + ( 3, 1, 4)^T ) = ( -2, 0, 2)^T · (1, -1, 1)^T + ( -2, 0, 2)^T · ( 3, 1, 4)^T = 0 + 2 = 2

خاتمة

وضّحنا في هذا المقال مفهوم الجداء النقطي للأشعة وخاصياته، وسنناقش في المقال التالي كيفية ارتباط الجداء النقطي بطول الشعاع.

ترجمة -وبتصرُّف- للفصل The Dot Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.

اقرأ أيضًا

• المقال السابق: تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D
• خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد
• خاصية الطول Length للأشعة الهندسية في التصاميم ثلاثية الأبعاد