لقد تعرفنا في المقالات السابقة على على كيفية ضرب المصفوفات بمصفوفة عمودية وكذلك كيفية حساب عمليات ضرب المصفوفات لعمل تصاميم ثلاثية الأبعاد 3D وغيرها، وسنتابع في هذا المقال، شرح آخر نوع من عمليات ضرب المصفوفات، إذ يوضّح هذا المقال خاصيات أخرى لعملية ضرب المصفوفات، خاصةً المصفوفة المحايدة Identity Matrix ومعكوس المصفوفة Matrix Inverse.
سنوضّح في هذا المقال المواضيع التالية:
- المصفوفة المحايدة: IA = AI = A
- المصفوفة المحايدة هي مصفوفة فريدة
- منقول Transpose المصفوفة المحايدة: IT = I
- ضرب المصفوفة المحايدة بنفسها: II = I
- المصفوفة المحايدة الموجودة في المنتصف بين مصفوفتين: AIB = AB
- معكوس مصفوفة: AA-1 = A-1A = I
- المصفوفات المفردة Singular وغير المفردة Non-singular
- معكوس المصفوفة هو مصفوفة فريدة
- معكوس ضرب مصفوفتين:
(AB)-1 = B-1 A-1
-
معكوس منقول المصفوفة:
(A-1)T = (AT)-1
-
محدِّد Determinant المصفوفة المفردة
ستكون جميع المصفوفات في هذا المقال مصفوفات مربعة؛ فالمصفوفة المربعة هي المصفوفة التي يكون فيها عدد الصفوف مساويًا لعدد الأعمدة.
الضرب الملحق Post-multiplication للمصفوفات في المصفوفة المحايدة
تستخدم الرسوميات الحاسوبية المصفوفات المربعة لأغراض متعددة؛ إذ تُطبَّق معظم عمليات التحويل Transformations، مثل تغيير مجال الرؤية في العالم ثلاثي الأبعاد أو عرضها على صورة ثنائية الأبعاد، باستخدام المصفوفات المربعة.
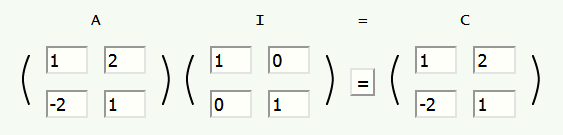
وكما هو معروف، للمصفوفات المربعة خاصيات لا تتشارك فيها مع المصفوفات الأخرى، لذا سنتعرف أولًا على إحدى هذه الخاصيات من خلال إجراء عملية الضرب التالية:
وبالتالي نلاحظ أن الضرب الملحق لمصفوفةٍ ما بالمصفوفة المحايدة يعطي المصفوفة نفسها:
AI = A
الضرب المسبق Pre-multiplication للمصفوفات بالمصفوفة المحايدة
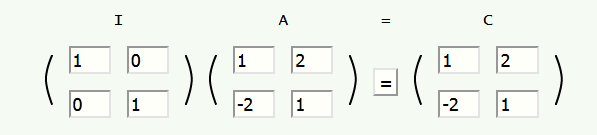
لنجرِ الآن عملية الضرب التالية:
سنلاحظ أن الضرب المسبق لمصفوفةٍ ما بالمصفوفة المحايدة يعطي المصفوفة نفسها:
IA = A
المصفوفة المحايدة Identity Matrix
تُسمَّى المصفوفة I بالمصفوفة المحايدة، لأن ضرب المصفوفة بها، يعطي المصفوفة نفسها: IA = A و AI = A، وذلك مهما كانت المصفوفة A؛ وهي مشابهة للعدد الحقيقي 1 الذي يمثل العنصر المحايد لعملية ضرب الأعداد الحقيقية، لأن 1a = a و a1 = a لجميع الأعداد الحقيقية a.
لا توجد مصفوفة محايدة مُحدَّدة للمصفوفات بجميع أبعادها؛ إذ تكون المصفوفة IN×N مصفوفةًَ محايدةً للمصفوفات المربعة التي أبعادها N×N فقط، فمثلًا المصفوفة المحايدة للمصفوفات التي أبعادها 3×3 هي:
نضع العدد 1 مكان عناصر القطر الرئيسي Main Diagonal للمصفوفة المحايدة ذات N بُعد IN×N، والعدد 0 للعناصر الأخرى في المصفوفة؛ إذ يتكون القطر الرئيسي من العناصر التي يتساوى فيها رقم الصف مع رقم العمود، ويجب أن تكون الأرقام من النوع 1 على هذا القطر، وليس على القطر الآخر.
المصفوفة المحايدة هي مصفوفة فريدة
لا توجد مصفوفة أخرى أبعادها N×N تماثل في عملها المصفوفة المحايدة؛ فبما أن العدد 1 فريدٌ بالنسبة للأعداد الحقيقية، فإن المصفوفة المحايدة هي مصفوفةٌ فريدة بالنسبة للمصفوفات التي أبعادها NxN، وسنبرهن ذلك فيما يلي:
لنفترض أن جميع المصفوفات لها الأبعاد الصحيحة لعملية الضرب، وأن هناك مصفوفة Z تحقق ما يلي:
ZA = A (1)
مهما كانت المصفوفة A التي لها الأبعاد الصحيحة، فستعمل المصفوفة Z مثل عمل المصفوفة I، ولكن نأمل أن تكون مختلفةً عنها؛ أما بالنسبة للمصفوفة B فنعلم أن ضرب مصفوفة B بالمصفوفة المحايدة يعطي المصفوفة B نفسها مهما كانت المصفوفة B التي لها الأبعاد الصحيحة.
BI = B (2)
لنضع المصفوفة المصفوفة I مكان المصفوفة A في العلاقة رقم (1)، بما أن A يمكن أن تكون أي مصفوفة مناسبة.
ZI = I (3)
ولنضع الآن المصفوفة Z مكان المصفوفة B في العلاقة رقم (2):
ZI = Z (4)
لاحظ من العلاقتين (3) و(4) أن Z و I متساويين مع الشيء نفسه، لذا يجب أن يكونا متساويين.
Z = I (5)
يمكنك البدء مرةً أخرى من الخطوة رقم (1) بالترتيب الآخر AZ = A والوصول إلى النتيجة ذاتها؛ لذا إذا وجدت مصفوفةً تعمل مثل عمل المصفوفة المحايدة، فهي بالتأكيد المصفوفة المحايدة بحد ذاتها.
خاصيات أخرى للمصفوفة المحايدة
لنوضح الآن بعد الخاصيات الأخرى للمصفوفة المحايدة. على سبيل المثال، يُعَد منقول المصفوفة المحايدة هو المصفوفة المحايدة نفسها:
IT = I
وهناك خاصية أخرى مفيدة للمصفوفة المحايدة، والتي تُعَد مجرد تطبيقٍ لتعريفها؛ حيث إذا جاءت المصفوفة المحايدة بين مصفوفتين، فلن تؤثر على عملية الضرب:
AIB = AB
كما أن مربع المصفوفة المحايدة هو المصفوفة المحايدة نفسها:
I I = I
أو
I2 = I
تُعَد هذه الخاصيات واضحةً ولا حاجة لحفظها.
المصفوفة القطرية Diagonal Matrix
تُعَد المصفوفة القطرية (a I) مفيدةً أحيانًا في الرسوميات الحاسوبية. لنفترض مثلًا أننا نريد حساب الآتي، بحيث يكون a عدد حقيقي و x مصفوفة عمودية:
a Ax
هنا وبحالات كثيرة، سنجد أنه من المفيد أحيانًا التفكير على النحو التالي:
(a I) Ax
وبهذا تكون قد أصبحت جميع العمليات عبارة عن عمليات ضرب مصفوفات، ويُعَد ذلك ميزة، نظرًا لأنه يمكن إجراء عملية ضرب المصفوفات باستخدام عتاد الرسوميات الحاسوبية دون الحاجة لحسابها.
لنحاول الآن إيجاد ناتج ضرب المصفوفتين التاليتين بأبسط طريقة كما يلي:
عملية ضرب المصفوفات التي ينتج عنها المصفوفة المحايدة
من الواضح أن:
(2 I)(0.5 I) = 2 (0.5) I = 1 I = I
ولكن جرّب ضرب هاتين المصفوفتين بالطريقة العادية:
لاحظ أن الصفوف من المصفوفة الأولى تتلاءم مع أعمدة المصفوفة الثانية، بحيث يساوي حاصل الجداء النقطي لها القيمة 1 لعناصر القطر الرئيسي فقط؛ بينما تساوي جميع عمليات الجداء النقطي الأخرى القيمة 0، وبالتالي فالمصفوفة الناتجة هي المصفوفة المحايدة I.
معكوس المصفوفة
لنفترض أن ax = b للأعداد الحقيقية a و b، وأن المتغير الحقيقي هو x، ولنوجد قيمة x الآن.
إذا كان ax = b، فإن (a-1) ax = (a-1)b، أو x = (a-1)b، إلّا عندما يكون العدد a صفرًا؛ فالقيمة (a-1) هي معكوس العدد a، وجميع الأعداد الحقيقية غير الصفرية لها معكوس. توجد فكرة مماثلة خاصة بالمصفوفات المربعة، وليكن لدينا مثلًا:
Ap = q
لدينا: p و q هي أشعة عمودية، أما A فهي مصفوفة أبعادها n×n. ومع افتراض أن A و q معلومتان:
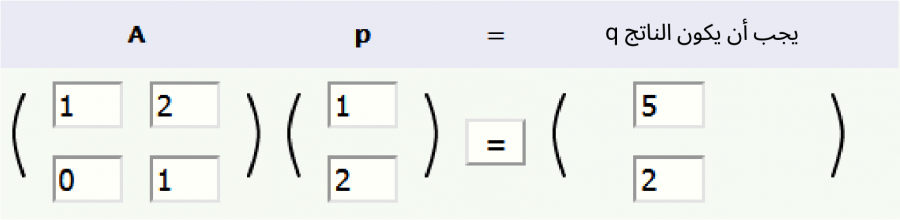
لنجرّب معرفة قيمة المصفوفة العمودية p للوصول إلى النتيجة التالية:
يُعَد إيجاد قيمة p بالتخمين أمرًا صعبًا، وسيكون الأمر أسوأ بكثير إذا كانت أبعاد المصفوفة A هي 5 × 5؛ لذا توجد طريقة أفضل لذلك، وهي باستخدام معكوس المصفوفة.
إذًا، لتكن لدينا p و q مصفوفات عمودية و A مصفوفة أبعادها N×N، حيث تكون قيمة q و A معلومتين، ونريد معرفة قيمة p:
q = Ap (1)
لنفترض وجود مصفوفة BN×N تحقق ما يلي:
p = Bq (2)
إذا وُجِدت مثل هذه المصفوفة، فيمكننا حساب ما نريده (أي المصفوفة p) من المصفوفة q، لذا عوّض ما توصلت إليه من العلاقة رقم (2) في العلاقة رقم (1):
q = A (Bq) (3)
q = (AB) q (4)
إذا كانت العلاقة رقم (4) صحيحة، فإن (AB) = I. وعلينا هنا أن نتذكّر أن المصفوفة المحايدة هي مصفوفة فريدة.
إذا كانت المصفوفة B موجودةً فعلًا، فهي تُعَد معكوسًا للمصفوفة A، وتُكتَب بالشكل: A-1؛ وبالتالي يمكننا الآن إيجاد قيمة p في العلاقة رقم (1) من خلال ضرب كل طرف منها في المعكوس A-1كما يلي:
A-1 q = A-1 Ap
A-1 q = p
المصفوفة غير المفردة Non-singular
ليس لجميع المصفوفات المربعة معكوس دائمًا، فالمصفوفة الصفرية مثلًا ليس لها معكوس؛ إذ لا توجد مصفوفة 0-1 تحقق الخاصية: 0 0-1 = I، ولكن الأمر أسوأ من ذلك، فالعديد من المصفوفات المربعة التي أبعادها N × N ليس لها معكوس.
تسمى المصفوفة التي لها معكوس: المصفوفة غير المفردة Non-singular، في حسن تسمى المصفوفة التي ليس لها معكوس: المصفوفة المفردة Singular.
إذا كانت المصفوفة A غير مفردة، فهي تحقق ما يلي:
AA-1= A-1A = I
لدينا هنا مثال عن مصفوفة لها معكوس:
وليكن لدينا مثلًا ما يلي:
بحيث يمكننا إيجاد قيمة p باستخدام المعكوس A-1 كما يلي:
معكوس المصفوفة هو مصفوفة فريدة
إذا كانت المصفوفة A غير مفردة (أي لها معكوس) وكان Ap = q، فإن p = A-1 q.
يُعَد معكوس المصفوفة المربعة غير المفردة فريدًا، وإحدى الطرق لإثبات ذلك هي وجود مصفوفة عمودية واحدة p فقط تُعَد حلًا للمعادلة Ap = q، لذلك يجب أن يكون هناك معكوس A-1 واحد فقط للمصفوفة. ويُعَد المعكوس A-1 مفيدًا في المناقشات حول المصفوفات وعمليات التحويل، ولكنه ليس مفيدًا جدًا للحسابات الفعلية، لذا لا حاجة لحسابه أبدًا.
لنفترض مثلًا أن المصفوفة العمودية p تمثل نقطةً في عالم الرسوميات الحاسوبية، وأنه في حال تغير مجال الرؤية، فستُحوَّل المصفوفة العمودية إلى العلاقة .q = Ap قد يفكر الكثيرون هنا بعكس التحويل باستخدام A-1 q، ولكن هناك دائمًا طريقة أسهل للعودة إلى مجال الرؤية الأصلي بدلًا من حساب المعكوس.
لنحاول إيجاد ناتج (AB) (B-1 A-1) كما يلي:
باستخدام خاصية التجميع:
(AB) (B-1 A-1) = A (B B-1) A-1
= A I A-1 = A A-1 = I
خاصيات معكوس المصفوفة
يساوي معكوس ضرب مصفوفتين نتيجة ضرب معكوس المصفوفة الثانية بمعكوس المصفوفة الأولى؛ فقد عكسنا ترتيب المصفوفات كما يلي:
(AB)-1 = B-1 A-1
وتوجد خاصية أخرى مفيدة وهي:
(A-1)T = (AT)-1
محدد Determinant المصفوفة المفردة
يمكن حساب محدِّد المصفوفة التي أبعادها 2 × 2 على النحو التالي:
إليك مثال لحساب محدّد مصفوفة:
يُعَد حساب محدد المصفوفات الأكبر أكثر تعقيدًا؛ إذ يندر تطبيقها، حيث يُستخدَم المحدّد عند مناقشة المصفوفات، وليس في العمليات الحسابية.
ملاحظة: يساوي محدّد المصفوفة المفردة الصفر.
رتبة Rank المصفوفة
إليك مثال آخر لحساب محدّد مصفوفة:
للمصفوفة في المثال السابق محدّد صفري، وبالتالي فهي مصفوفة مفردة، وليس لها معكوس، وتتكون من صفين متطابقين، وبالتالي يمكن القول بأن صفوفها غير مستقلة؛ فإذا كان أحد الصفوف مضاعفًا لصف آخر، فإننا نسمّيها صفوفًا غير مستقلة؛ إذ يساوي محدّد هذه المصفوفة الصفر. وبالمثل، إذا كان أحد الأعمدة مضاعفًا لعمود آخر، فسيكون هذين العمودين غير مستقلين، وبالتالي يكون محدّد هذه المصفوفة صفرًا.
رتبة المصفوفة هي الحد الأقصى لعدد الصفوف المستقلة (أو الحد الأقصى لعدد الأعمدة المستقلة)، وتكون المصفوفة المربعة An×n غير مفردة فقط إذا كانت رتبتها تساوي n.
لنجرب إيجاد رتبة المصفوفة التالية:
رتبة المصفوفة السابقة هي 3، حيث يُعَد الصف الأخير مضاعفًا للصف الأول.
خاتمة
بهذا نكون قد تعرفنا على مفهوم كل من المصفوفة المحايدة Identity Matrix ومعكوس المصفوفة وكيفية استخدامهما في عملية ضرب المصفوفات. وبهذا نكون قد وصلنا لنهاية هذه السلسلة التعليمية حول الأشعة وجبر المصفوفات من وجهة نظر رسومات الحاسوب، حيث غطينا عدة مواضيع عن الأشعة والمصفوفات وتعرفنا على عدة حالات للتعامل معها.
ترجمة -وبتصرُّف- للفصل Identity Matrix and Matrix Inverse من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.



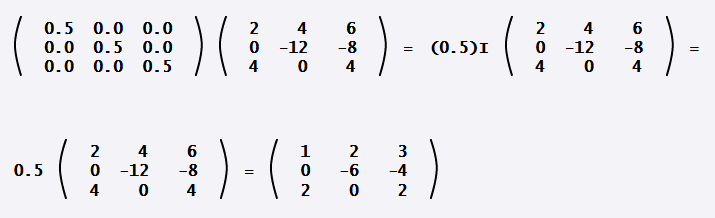
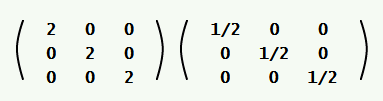
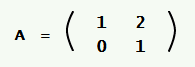
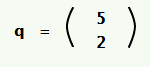

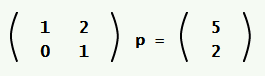
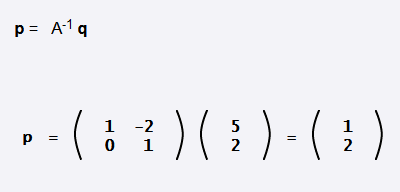
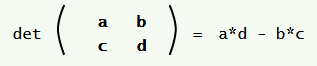
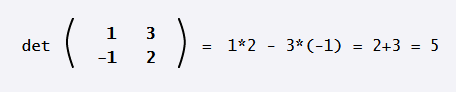
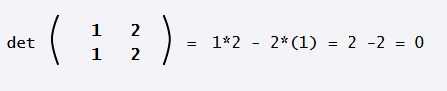











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.