إسقاط شعاع على شعاع آخر واستخداماته في الرسوميات الحاسوبية 3D

ناقشنا في مقالٍ سابق أن الرسوميات الحاسوبية ثلاثية الأبعاد تتكون من عمليتين: أولهما إنشاء عالم خيالي داخل الحاسوب، وثانيهما إنتاج صور ثنائية الأبعاد لذلك العالم من مجالات رؤية مختلفة؛ إذ يُعَد إنتاج صورة ثنائية الأبعاد من صورة ثلاثية الأبعاد مثالًا عن عملية الإسقاط Projection، وسنناقش في هذا المقال المفاهيم الأساسية فقط للإسقاط.

سنوضّح في هذا المقال المواضيع التالية:

تشكيل مستوٍ Plane واحد من شعاعين.
مفهوم الإسقاط.
إسقاط شعاعٍ على شعاع آخر.
صيغة لإسقاط الأشعة.
طريقة إسقاط الأشعة خطوةً بخطوة.
المكون العمودي لإسقاط الأشعة.
مثال لإسقاط الأشعة ثنائية الأبعاد.
مثال لإسقاط الأشعة ثلاثية الأبعاد.

المساقط ثنائية الأبعاد المتعددة

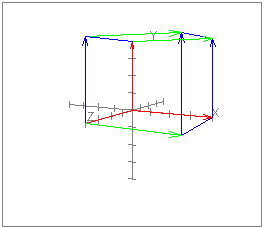
يمكن إنتاج عدد لا نهائي من الصور ثنائية الأبعاد من نموذج واحد ثلاثي الأبعاد، فمثلًا، يعرض الشكل التالي إسقاط نموذج ثلاثي الأبعاد لصندوق على عرضٍ ثنائي الأبعاد؛ إذ تنتِج المواقع المختلفة لمجال الرؤية صورًا مختلفة ثنائية الأبعاد، وتُسقَط الأشعة ثلاثية الأبعاد للنموذج على سطح العرض لتكوين أشعة الصورة ثنائية الأبعاد.

تشكيل مستوٍ واحد من شعاعين

يمكن تشكيل مستوٍ واحد باستخدام شعاعين ونقطة دائمًا، إلا في حال كان هذان الشعاعان متوازيان. لا بد أنك تتذكر من مادة الهندسة في المرحلة الثانوية أن الخطين غير المتوازيين (ليسا على استقامة واحدة) يحددان مستوٍ واحد، وبالتالي ينطبق الشيء نفسه على الأشعة. تبدأ معظم الأمثلة في هذا المقال بشعاعين ثنائي الأبعاد، ولكن ستكون النتائج صالحة لشعاعين ثلاثي الأبعاد؛ إذ يحدّد شعاعان ثلاثي الأبعاد مستوٍ واحد أيضًا.

يوضّح الشكل السابق الشعاع w والشعاع v، وجعلنا ذيل هذين الشعاعين يبدأ من النقطة نفسها لتسهيل التصور، ولكن لا تنسَ أن الأشعة ليس لها موضع محدّد، وجعلنا الشعاع v أفقيًا للسهولة أيضًا، ولكن يمكن أن يكون له أيّ منحى Orientation.

إسقاط شعاع على شعاع آخر

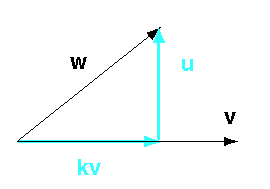
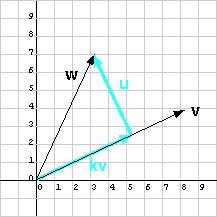
إذا ضربنا الشعاع v بعدد حقيقي Scalar (أو مقدار سلمي) k، فسيؤدي ذلك إلى تغيير طول هذا الشعاع، ولكنه لن يؤثر على منحاه، وبالتالي ليكن لدينا الشعاعان w و v كما في الشكل التالي:

يمكن أن يكون الشعاعان w و v أيّ شعاعين، ونريد شعاعًا u عموديًا على الشعاع v وعددًا حقيقيًا k مضروبًا به، بحيث:

w =‎ k v + u‎

ويسمى عندها k v‎ مسقط الشعاع w على الشعاع v.

صيغة لكيفية إسقاط الأشعة

ملاحظة: إذا كان الشعاعان u و v متعامدان، فإن الجداء النقطي لهما هو: ‎.u · v = 0

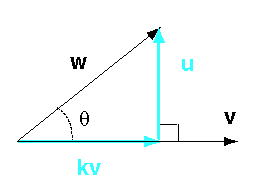
يجب أن تتحقق العلاقة: k v + u = w‎ بشرط أن يكون u عموديًا مع v، حتى يكون k v‎ مسقط الشعاع w على الشعاع v؛ إذ نعلم من علم المثلثات أن:

طول المسقط k v‎ =‫ ‎| w | cos θ.
منحى k v‎ هو شعاع الوحدة ‎v_u‎.

تذكر أن أشعة الوحدة Unit Vectors تُستخدَم لتمثيل المنحى في الفضاء ثلاثي الأبعاد، وبالتالي يكون منحى الشعاع v هو شعاع الوحدة ‎v_u‎؛ إذ يبدو المنحى أفقيًا في الشكل السابق، ولكننا استخدمنا ذلك للسهولة فقط. وبما أن cos θ يساوي ‎w_u · v_u‎، فسينتج ما يلي:

‎k v = | w | (w_u · v_u) v_u

يمثل الجزء ‎| w | (w_u · v_u)‎ عددًا حقيقيًا بحيث يُضبَط الشعاع v على الطول المطلوب، وهو طول الخط الأفقي باللون الأزرق الفاتح في الشكل السابق؛ بينما يعبّر الجزء المتبقي من الصيغة: ‎v_u‎ عن منحى الشعاع v نفسه.

طريقة إسقاط الأشعة خطوة بخطوة

تذكير: يمكنك حساب شعاع الوحدة من خلال تقسيم الشعاع على طوله.

لنتّبع طريقة خطوة بخطوة لإسقاط الشعاع w على v، بدلًا من حفظ الصيغة السابقة لتطبيق عملية الإسقاط.

أولًا، نحسب أطوال الأشعة كما يلي:

‎| w | = √(w · w)

‎| v | = √(v · v)

ثانيًا، نحسب أشعة الوحدة:

w_u = w / | w‎ |‎

v_u = | v | / | v |‎

ثالثًا، نحسب جيب تمام Cosine الزاوية بين الشعاعين:

w_u · v_u

رابعًا، نعوّض في صيغة الإسقاط التالية:

‎k v = | w | (w_u · v_u) v_u

المكون العمودي لإسقاط الأشعة

ملاحظة: لا يُعَد مسقط الشعاع w على الشعاع v مماثلًا لمسقط الشعاع v على الشعاع w، إذ يكون منحى الشعاع الناتج عن عملية الإسقاط بالاتجاه نفسه للشعاع المُسقَط عليه.

أوجدنا في الفقرة السابقة k v‎، لذا من السهل العثور على الشعاع المتعامد معه u:

‎w = k v + u‎، إذًا ‎u‎ = w - k v‎

تعبّر إشارة "+" في الصيغة السابقة عن جمع الأشعة، وتعبّر إشارة "-" عن طرح الأشعة.

تدريبات عملية

كانت الأشعة في هذا المقال جميعها أشعةً هندسيةً حتى الآن، إذ لم يكن هناك أيّ ذكرٍ للإطارات الإحداثية أو المصفوفات العمودية، ولكن ستنجح هذه النتائج عند تمثيل الأشعة بالمصفوفات العمودية كما سنرى في الأمثلة التالية.

تدريب 1:

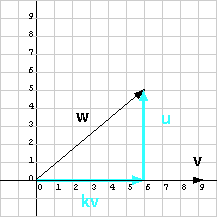
نمثّل الشعاع w بالمصفوفة العمودية ‎(6, 5)^T‎، ونمثّل الشعاع v بالمصفوفة العمودية ‎(9,0)^T‎، ولنوجد مسقط الشعاع w على الشعاع v، أي لنبحث عن الشعاعين k v‎ و u. يمكنك ببساطة قراءة الإجابة من الرسم البياني الورقي التالي، ولكن تظاهر أنك لم تلاحظ ذلك.

أولًا، نحسب الأطوال كما يلي:

‎| w | = √ ((6, 5)^T‎·(6, 5)^T‎) = 7.81‎

‎| ‎v | = √ ((9, 0)^T‎·(9, 0)^T‎) = 9

ثانيًا، نحسب أشعة الوحدة كما يلي:

‎w_u = (6, 5)^T / 7.81

‎v_u = (9, 0)^T / 9 = (1, 0)^T

ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين وهو:

‎w_u · v_u = (1/7.81) (6, 5)(1, 0)^T · (1, 0)(1, 0)^T = 6/7.81

رابعًا، نعوّض في صيغة الإسقاط التالية:

k v = | w | (w_u · v_u) v_u

‎‎k v = 7.81 (6/7.81) (1, 0)^T = 6(1, 0)^T = (6, 0)^T

خامسًا، نحسب الشعاع العمودي:

u = w - k v

‎u = (6, 5)^T - (6, 0)^T = (0, 5)^T

والنتيجة هي أن ‎u = (6,0)^T + (0,5)^T‎ كما هو متوقع. وكان هذا المثال سهلًا طبعًا.

ملاحظة: ليس عليك أن تحسب طول w، لأنه يُلغَى قبل الإجابة النهائية، لذا فكل ما تحتاج إليه هو مربع طول v، أي ‎|v|²‎؛ إذ تعرض بعض الكتب صيغًا مختلفة للإسقاط تستفيد من هذه الحقائق.

تدريب 2

إليك مثال آخر، ولكنه ليس بهذه السهولة، إذ نمثّل الشعاع w هنا بالمصفوفة العمودية ‎(3.2, 7)^T‎، ونمثّل الشعاع v بالمصفوفة العمودية ‎(8, 4)^T‎؛ ولنوجِد الآن الشعاعين k v‎ و u.

أولًا، نحسب الأطوال كما يلي:

| w | = (لا داعي لحسابه، لذا أبقيه بالرموز)

‎| v |² = (8, 4)^T ·(8, 4)^T = 80

ثانيًا، نحسب أشعة الوحدة وهي:

w_u = (3.2, 7)^T / | w |‎

v_u = (8, 4)^T / | v |‎

ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي:

‎w_u · v_u = (3.2, 7)^T / | w | · (8, 4)^T / | v | = 53.6 /( | w | | v |)‎

رابعًا، نعوّض في صيغة الإسقاط التالية:

‎k v = | w | (w_u · v_u) v_u

k v = | w | [53.6 / (| w | | v |)] (8, 4)^T / | v |‎

k v = 53.6 / (| v |) (8, 4)^T / | v |‎

‎k v = 53.6 / (| v |²) (8, 4)^T

‎k v = 53.6 / 80 (8, 4)^T

k v = ((53.6*8)/80, (53.6*4)/80)^T = ( 5.3, 2.68)^T

خامسًا، نحسب الشعاع العمودي:

u = w - k v

u = (3.2, 7)^T - (5.3, 2.68)^T = (-2.1, 4.32)^T

لنتحقّق الآن من أن: ‎w = k v + u‎ من خلال تعويض النتائج في العلاقة k v + u‎ كما يلي:

‎( 5.3, 2.68)^‎T + (-2.1, 4.32)^T = (3.2, 7.0)^T = w

فوائد عملية إسقاط الأشعة

يجب أن تفهم جيدًا ما يحدث عند إسقاط شعاع على شعاع آخر، إذ تحدث عملية الإسقاط -كما ذكرنا سابقًا- باستمرار عندما يعرض الحاسوب الرسوميات. تُنفَّذ معظم العمليات الحسابية في عتاد الرسوميات الخاصة بالحاسوب، ويجري إسقاط ملايين الأشعة في الثانية الواحدة؛ فإذا أردتَ أن تعرف ما يحدث في الرسوميات الحاسوبية، فيجب أن تعرف ما هي عملية الإسقاط.

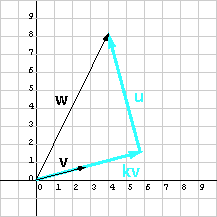
لنوجِد الآن مسقط الشعاع w على الشعاع v في الرسم البياني التالي:

حاول إجراء العمليات الحسابية المطلوبة كما فعلنا في الأمثلة السابقة، ولكن يمكن أن تحصل على الإجابات التالية مباشرةً من قراءة الرسم البياني السابق:

w = (4, 8.2)^T

v = (2.8, 1.75)^T

k v = (5.8, 1.6)^T

u = (-1.8, 6.4)^T

تبدو الإجابات السابقة جيدة، ولكن لنتحقّق منها كما يلي:

أولًا، هل ‎w = k v + u‎؟

‎(5.8, 1.6)^T + (-1.8, 6.4)^T = (4, 8.0)^T = w

(حسنًا، تقريبًا)

ثانيًا، هل ‎v · u = 0.0؟

‎(5.8, 1.6)^T · (-1.8, 6.4)^T = -10.44 + 10.24 = -0.2 = ‎0.0‎

(تقريبًا)‎

ملاحظة: لنفكر في جميع الأشعة المحتملة w و v ومسقط الشعاع w على الشعاع v، إذ يمكن أن يكون الشعاع k v‎ أطول من الشعاع v كما في المثال السابق، ولكن لا يمكن أن يكون الشعاع k v‎ أطول من الشعاع w، فأكبر طول ممكن للشعاع k v‎ هو | w | عندما يكون w و v على استقامة واحدة.

مثال آخر لعملية الإسقاط

لاحظ أن عملية إسقاط الشعاع w على v لا تعتمد على طول v، بل يؤثر اتجاه الشعاع v فقط على النتائج. يكون طول المسقط هو ‎| w | cos θ، حيث θ هي الزاوية بين الشعاعين، وبما أن دالة جيب التمام لا تزيد عن 1 أبدًا، فلن يكون طول المسقط أبدًا أطول من الشعاع المُسقَط.

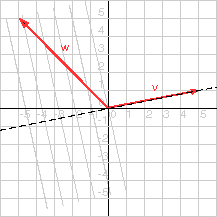
أسقِط الشعاع w على الشعاع v من خلال الاطلاع على الرسم البياني التالي:

وستحصل على الإجابات التالية:

w = (-5, 5)^T

v = (5, 1)^T

k v = (-3.8, -.8)^T

u = (-1.3, 5.6)^T

حصلنا على الإجابات السابقة من خلال قراءة الرسم البياني السابق، ولكنها ليست دقيقة بالضرورة، إذًا لنتحقّق منها.

أولًا، هل ‎w = k v + u‎؟

‎(-3.8, -0.8)^T + (-1.3, 5.6)^T = (-5.1, 4.8)^T = w

(تقريبًا)

ثانيًا، هل ‎v · u = 0.0؟

‎‎(5, 1)^T · (-1.3, 5.6)^T = -6.5 + 5.6 = -0.9 = 0.0

(ليس تمامًا)

ملاحظة: يمكن لمسقط الشعاع w على الشعاع v أن يؤشّر إلى الاتجاه المعاكس للشعاع v كما حدث في المثال السابق.

أمثلة لإسقاط الأشعة ثلاثية الأبعاد

سنستعرض هنا بعض الأمثلة حول كيفية إسقاط الأشعة ثلاثية الأبعاد

المثال الأول

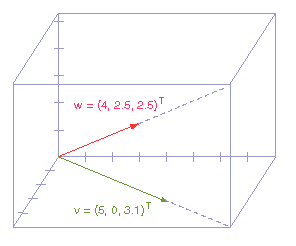
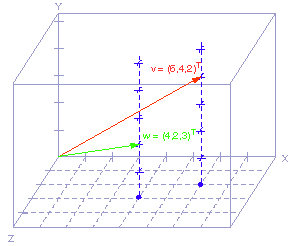
يظهر الرسم البياني السابق الشعاعين التاليين:

‎w = (4, 2.5, 2.5)^T‎ (الشعاع الأحمر)

‎v = (5, 0, 3.1)^T (الشعاع الأخضر)

أسقِط الشعاع w على الشعاع v، وتذكّر أن طول الشعاع v لا يؤثر على الإسقاط، بل يؤثر منحاه عليه فقط، لذا أنزِل رأس سهم الشعاع w على الخط المنقط.

يمكن بالنظر تقدير مسقط الشعاع ‎w = (4, 2.5, 2.5)^T‎ على الشعاع ‎v = (5, 0, 3.1)^T‎ بأنه k v = (4, 0, 2.5)^T‎.

يتضمن إسقاط الشعاع w على الشعاع v في هذه الحالة "انهيار Collapsing" البعد y للشعاع w. فلنتحقّق الآن مما إذا كانت النتيجة نفسها رياضيًا، إذ يمكن تطبيق الخطوات نفسها في الفضاء ثلاثي الأبعاد 3D.

أولًا، نحسب الأطوال وهي:

| w | = (لا داعي لحسابه، لذا أبقيه بالرموز)

‎| v |² = ((5, 0, 3.1)^T · (5, 0, 3.1)^T) = 34.61

ثانيًا، نحسب أشعة الوحدة كما يلي:

w_u = (4, 2.5, 2.5)^T / | w |‎

v_u = (5, 0, 3.1)^T / | v |‎

ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي:

‎w_u · v_u = (4, 2.5, 2.5)^T / | w | · (5, 0, 3.1)^T / | v | = 27.75 / ( | w | | v |)

رابعًا، نعوّض في صيغة الإسقاط التالية:

‎k v = | w | (w_u · v_u) v_u‎

k v = | w | (27.75 / (| w | | v |)) (5, 0, 3.1)^T / | v |‎

k v = 27.75 / (| v |) (5, 0, 3.1)^T / | v |‎

‎k v = 27.75 / (| v |²) (5, 0, 3.1)^T

k v = (27.75 / 34.61) (5, 0, 3.1)^T‎

‎k v = ((27.75*5)/34.61, 0, (27.75*3.1)/34.61)^T

‎k v = ( 4.00, 0, 2.49)^T

وبالتالي فإن التقدير بالنظر k v = (4, 0, 2.5)^T‎ يطابق النتيجة الرياضية ‎(4, 0, 2.5)^T‎، ويمكن الآن بسهولة حساب الشعاع العمودي:

u = w - k v

u = (4, 2.5, 2.5)^T - (4, 0, 2.5)^T = (0, 2.5, 0)^T

أبقِ الشعاع w كما هو في الرسم البياني السابق، وحاول تصوّر إسقاط w على شعاع مختلف v'‎ ينتج عنه المسقط k ،v'‎ الذي يؤدي إلى انهيار البعدين y و z للشعاع w؛ فمثلًا، إذا أسقطنا الشعاع ‎w = (4, 2.5, 2.5)^T‎ على الشعاع ‎v' = (1, 0, 0)^T‎، فستكون النتيجة k v = (4, 0, 0)^T‎.

المثال الثاني

إذا أسقطنا شعاعًا في فضاء ثلاثي الأبعاد على محاور إحداثية، فستحصل على أحد الأبعاد الثلاثة فقط لذلك الشعاع، لذا لنلقِ نظرة على مثال آخر أصعب.

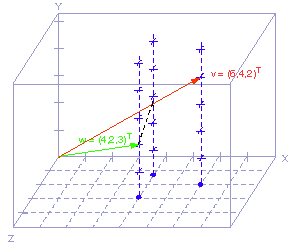
لدينا من الشكل السابق الشعاعان ‎w = (4, 2, 3)^T‎ و ‎v = (6, 4, 2)^T‎، ونريد إسقاط الشعاع w على الشعاع v.

يمكن أن نقدّر بالنظر أنه إذا "أنزلنا" رأس سهم الشعاع w عموديًا على الشعاع v، فستصل إلى الشعاع v عند حوالي 4/10 من طول v، لذا فإن k تساوي 0.4 تقريبًا و k v‎ يساوي:

k v = 0.4 (6, 4, 2)^T = (2.4, 1.6, 0.8)^T

ولكن سيتضح معنا أن هذه النتيجة التقديرية خاطئة بصورة فادحة، إذ يُعَد إيجاد الحل بالنظر في المسائل ثلاثية الأبعاد أمرًا صعبًا، إلّا إذا كانت لديك صورة ثلاثية الأبعاد فعلية أمامك. على هذا الأساس، دعنا نتحقق من الإجابة رياضيًا.

أولًا، نحسب الأطوال وهي:

| w | = (لا داعي لحسابه، لذا أبقيه بالرموز)

‎| v |² = ((6, 4, 2)^T · (6, 4, 2)^T) = 56

ثانيًا، نحسب أشعة الوحدة كما يلي:

w_u = (4, 2, 3)^T / | w |‎

v_u = (6, 4, 2)^T / | v |‎

ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي:

w_u · v_u = (4, 2, 3)^T · (6, 4, 2)^T / | w | | v | = 38 / ( | w | | v |)

رابعًا، نعوّض في صيغة الإسقاط التالية:

k v = | w | (w_u · v_u) v_u

k v = | w | {38 / (| w | | v |)} {(6, 4, 2)^T / | v |}

k v = {38 / | v |} {(6, 4, 2)^T / | v |}

k v = {38 / | v |²} (6, 4, 2)^T

k v = {38/56} (6, 4, 2)^T

k v = 0.679 (6, 4, 2)^T

k v = ( 4.07, 2.7, 1.36)^T

لنحسب الآن الشعاع u كما يلي، حيث ‎u + k v = w‎ (الشعاع u هو الشعاع الأسود المنقط في الرسم البياني السابق):

u + k v = w

u = w - k v = (4, 2, 3)^T - ( 4.07, 2.7, 1.36)^T = (-0.07, -0.7, 1.64)^T

بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية إسقاط شعاع على شعاع آخر في فضاء ثنائي وثلاثي الأبعاد، وسنتعرّف في المقال التالي على عملية الجداء الشعاعي للأشعة.

ترجمة -وبتصرُّف- للفصل Projecting one Vector onto Another من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.