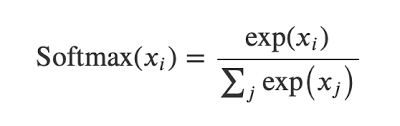Ali Haidar Ahmad

الخطأ هنا من المكان الذي تستورد فيه دالة التكلفة CategoricalCrossentropy، فهذه الدالة يمكن استخدامها كدالة تكلفة وكمعيار لقياس الدقة. ففي حالة كنت تريد استخدامها كدالة تكلفة يجب عليك استيرادها من الموديول losses أما إذا أردت استخدامها كمعيار فعيلك استيرادها من الموديول metrices أي يصبح نموذجك كالتالي: from keras import layers from keras import models model = models.Sequential() model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.Flatten()) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(10, activation='softmax')) from keras.datasets import mnist import keras from tensorflow.keras.utils import to_categorical (train_images, train_labels), (test_images, test_labels) = mnist.load_data() train_images = train_images.reshape((60000, 28, 28, 1)) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape((10000, 28, 28, 1)) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model.compile(optimizer='rmsprop', loss=keras.losses.CategoricalCrossentropy(), metrics=["acc"]) model.fit(train_images, train_labels, epochs=5, batch_size=64) test_loss, test_acc = model.evaluate(test_images, test_labels) # 99% حيث أنه أعطاك خطأ يعبر عن عدم قدرته على حساب المشتقات وذلك لأنه لم يتعرف على دالة التكلفة التي قمت بتمريرها.

يمكننا استخدام الدالة empty لإنشاء مصفوفة ثم القيام بتعبئتها بالقيمة المطلوبة من خلال التابع fill كما يلي: def fill(n): arr = np.empty(n) return arr.fill(np.nan) fill(5) # array([nan, nan, nan, nan, nan]) def fill(n): arr = np.empty(n) arr.fill(np.nan) return arr print(fill((3,2))) """ [[nan nan] [nan nan] [nan nan]] """ أو يمكنك أن تقوم يتعبئتها بشكل يدوي: def c(n): a = np.empty(n) a[:] = np.nan return a print(c((3,2))) """ [[nan nan] [nan nan] [nan nan]] """ وكطريقة سهلة يمكنك استخدام التابع full بحيث نمرر له أبعاد المصفوفة والقيمة المراد تعبئتها: def full(n): return numpy.full(n, np.nan) print(c((3,2))) """ [[nan nan] [nan nan] [nan nan]] """ أو من خلال التابع التالي حيث سنعتمد على مفهوم القوائم ثم تحويلها لمصفوفة نمباي: def list(n,row,col): return np.array(n * [np.nan]).reshape(-1,col) print(list(12,3,4)) """ [[nan nan nan nan] [nan nan nan nan] [nan nan nan nan]] """ لكن هنا نمرر عدد عناصر المصفوفة المطلوبة وعدد أسطر وأعمدة المصفوفة المطلوبة. ويمكنك أيضاً تنفيذ ماتريده بالشكل التالي: np.nan * np.zeros(shape=(3,2)) """ array([[nan, nan], [nan, nan], [nan, nan]]) """ كما ويمكنك من خلال الدالةtile حيث نمرر لها القيمة ثم الأبعاد كما في المثال التالي : np.tile(np.nan, (2, 3)) """ array([[nan, nan, nan], [nan, nan, nan]]) """ وبشكل عام فإن أسرع طريقة هي استخدام الدالة fill.

أولاً يجب أن نفهم المشكلة. ال unit vector أو متجه الوحدة هو متجه طويلته (magnitude) تساوي ال 1. وبالتالي فإن الشعاع التالي لايمثل متجه وحدة: import numpy as np # تعريف الشعاع التالي v = np.array([1,3]) # حساب الطويلة np.linalg.norm(v) #3.1622776601683795 # إذاً ليس متجه وحدة حيث أن التابع np.linalg.norm(x) يقوم بحساب الطويلة للشعاع. الآن إذا أردنا أن نقوم بتحويل هذا الشعاع إلى متجه وحدة فيجب أن نقوم بعملية normalizing. رياضياً فإنه لتحويل أي شعاع إلى شعاع وحدة يجب أن نقوم بقسمة جميع عناصره على طويلته، أي لتحويل الشعاع السابق يجب أن نقوم بقسمة قيمه على 3.16227766. import numpy as np v = np.array([1,3]) magnitude =np.linalg.norm(v) # نقسم كل عنصر على الطويلة v=v/magnitude # نختبر إذا أصبح متجه وحدة np.linalg.norm(v) # 1.0 # نجحنا حسناً إذا أردت أن لاتستخدم np.linalg.norm(v) يمكنك استخدام الصيغة التالية، فكما نعلم أن الطويلة هي الجذر التربيعي لمجموع مربعات قيم الشعاع: import numpy as np v = np.array([1,3,5,6,33]) magnitude =np.sqrt(np.sum(v**2)) # نقسم كل عنصر على الطويلة v=v/magnitude # نختبر إذا أصبح متجه وحدة np.linalg.norm(v) # 1.0 # نجحنا كما ويمكنك استخدام مكتبة Sklearn حيث تحتوي على طرق فعالة متاحة للمعالجة المسبقة للبيانات وأدوات التعلم الآلي الأخرى. عادةً ما يستخدم التابع normalize في هذه المكتبة مع المصفوفات ثنائية الأبعاد وتوفر خيار تسوية L1 و L2. سنستخدم في الكود التالي هذه التابع مع مصفوفة 1D حيث سنقوم باستخدام الدالة ravel لتسطيح المصفوفة : import numpy as np from sklearn.preprocessing import normalize v = np.array([1,3,5,6,33]) v = normalize(v[:,np.newaxis], axis=0).ravel() # نختبر إذا أصبح متجه وحدة np.linalg.norm(v) # 1.0 # نجحنا ,وأخيراً يمكنك استخدام الدالة الجاهزة لتحويل الشعاع إلى شعاع وحدة بشكل مباشر من خلال المكتبة transformations: # لتحميلها : pip install transformations import numpy as np import transformations as trafo v = np.array([1,3,5,6,33]) unit_v = trafo.unit_vector(data, axis=1) # نختبر إذا أصبح متجه وحدة np.linalg.norm(unit_v) # 1.0

.

الطريقة الوحيدة في نمباي من خلال التابع percentile : import numpy as np arr = np.array([1,2,3,4,5]) # نريد القيمة الأكبر من نصف عناصر المصفوفة per = np.percentile(arr, 50) # 3.0 # القيمة الأكبر من 90 بالمئة من عناصر المصفوفة np.percentile(arr, 90) # 4.6 np.percentile(arr, 100) # 5.0 np.percentile(arr, 0) # 1.0 حيث نمرر له المصفوفة والنسبة المئوية التي نريده أن يرد لنا القيمة الموافقة لها. وإذا أردت أن يتم تقريب قيم الخرج لأقرب قيمة. أي مثلاً بدلاً من 4.6 تريد 4 أو 5 فيمكنك القيام بذلك كالتالي: import numpy as np arr = np.array([1,2,3,4,6]) np.percentile(arr, 90, interpolation='lower') # 4 # التقريب للأعلى np.percentile(arr, 90, interpolation='higher') # 6 مثال آخر: a = np.array([[10, 7, 4], [3, 2, 1]]) """ array([[10, 7, 4], [ 3, 2, 1]]) """ np.percentile(a, 50) # 3.5 np.percentile(a, 50, axis=0) # array([6.5, 4.5, 2.5]) np.percentile(a, 50, axis=1) # array([7., 2.]) np.percentile(a, 50, axis=0, out=out) """ array([6.5, 4.5, 2.5]) """ np.percentile(a, 50, axis=1, keepdims=True) """ array([[7.], [2.]]) """ حيث أن الوسيط axis يمثل المحور أو المحاور التي سيتم حساب النسب المئوية على طولها. الافتراضي هو حساب النسب المئوية على طول نسخة مسطحة من المصفوفة. أما الوسيط out فيمثل مصفوفة إخراج بديلة لوضع النتيجة فيها. يجب أن يكون له نفس الشكل وطول المخزن المؤقت للإخراج المتوقع ، ولكن سيتم إرسال نوع (الإخراج) إذا لزم الأمر. ويمكنك من خلال التابع التالي القيام بذلك حيث سنستعين بالمكتبة الرياضية في بايثون: import numpy as np arr = np.array([1,2,3,4,5]) import math def per(data, perc: int): return sorted(data)[int(math.ceil((len(data) * perc) / 100)) - 1] per(arr,50) # 3 per(arr,90) # 5 # لاحظ أنه لم يعطي 4.6 per(arr,92) # 5 لكن هنا كما تلاحظ قام بعملية تقريب بحيث تكون القيمة ضمن المصفوفة أي لن يحتسب مجالات القيم. ويمكنك أيضاً القيام بذلك من خلال التابع التالي: import numpy as np arr = np.array([1,2,3,4,5]) def per(N, P): n = int(round(P * len(N) + 0.5)) return N[n-1] per(arr,0.5) # 3 per(arr,0.9) # 5

يجب أن تقوم بتحديد دالة لحساب التكلفة أي (loss function) فعدم تحديد دالة التكلفة يجعل نموذجك عاجزاً عن حساب ال gradients أو المشتقات، فال gradients تنتج من اشتقاق تابع التكلفة بالنسبة للأوزان التدريبية. وبالتالي يظهر الخطأ. وكون مهمتك هي مهمة تصنيف ثنائي فيمكنك استخدام ال BinaryCrossentropy كدالة تكلفة ممتازة جداً لمشكلتك ولأغلب مشاكل التصنيف الثنائي. أي قم بتعديل نموذجك بالشكل: from keras.layers import Embedding from keras.datasets import imdb from keras import preprocessing import keras max_features = 10000 maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) x_train = preprocessing.sequence.pad_sequences(x_train, maxlen=maxlen) x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) from keras.models import Sequential from keras.layers import Flatten, Dense model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) ############################## هنا ######################### model.compile(optimizer='rmsprop', loss=keras.losses.BinaryCrossentropy(), metrics=['BinaryAccuracy']) ####################################################### history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2) وفي الرابط هنا تجد توضيح كامل لهذه الدالة:

يخبرك الخطأ بأن أبعاد بيانات التدريب لديك (الدخل) هي (50000, 32, 32, 3) بينما أنت قمت بتعريف النموذج على أن تستقبل طبقة الدخل الخاصة به input_shape أبعاد من الشكل (3, 32, 32) أي input_shape=(3, 32, 32) وبالتالي ظهر الخطأ نتيجة عدم توافق الأبعاد. أي أن شكل الإدخال المتوقع والبيانات المعطاة مختلفين. ولحل المشكلة يجب أن تقوم بتعديل أبعاد طبقة الدخل في نموذجك أي input_shape=(32, 32, 3) أو أن تقوم بتغيير أبعاد الدخل يحيث يتوافق مع طبقة الدخل في نموذجك: x_train = x_train.transpose(0,3,1,2) x_test = x_test.transpose(0,3,1,2)

تقوم هذه الدالة بحساب مدى دقة النموذج، وتستخدم مع مهام التصنيف، عندما يكون الترميز الخاص بال label هو One-Hot وترد هذه الدالة قيمة عشرية بين 0 و 1 بحيث كلما اقتربت القيمة من 1 كانت دقة النموذج أعلى. وتقوم هذه الدالة بحساب عدد المرات التي قام فيها نموذجنا بتوقع القيم بشكل صحيح (عدد مرات الإصابة في التنبؤ أو بمعنى آخر عدد مرات التطابق) وتقسمها على عدد التوقعات الكلية (الصحيحة والخاطئة أي حالات التطابق وعدم التطابق). والمثال التالي سيوضح كل شيء، حيث قمت في البداية بكتابة كود بشكل يدوي لتحقيق هذا التابع ثم استخدمت كيراس: # تحميل المكتبات import numpy import tensorflow as tf #One-Hot تشكيل مصفوفتين واحدة للقيم الحقيقية مرمزة بترميز label = numpy.array([[0,0,0,1,0],[0,0,1,0,0],[0,0,1,0,0],[0,1,0,0,0]]) # الثانية تمثل القيم المتوقعة Pred = numpy.array([[0,0.2,0,1,0],[0,0.3,0,1,0],[0.12,0.2,0.6,0.7,0.1], [0.6,0.9,0,0,0]]) #argmax() استخدام تابع لامدا لتحديد الفهرس الذي يملك أعلى قيمة باستخدام التابع max = lambda x : numpy.argmax(x) # باستخدام التابع الذي قمنا بتعريفه سنقوم بتشكيل قائمتين لكل من القيم المتوقعة والحقيقية، تحوي فهارس القيم (الفهرس الذي يقابل أعلى قيمة) لكي نستخدمها في عملية المقارنة # مثال: [0,0,0,1,0]-->3 labelMax = numpy.array([max(n) for n in label]) print("labelMax: ",labelMax,sep="\n") # [3 2 2 1] PredMax = numpy.array([max(n) for n in Pred]) print("PredMax: ",PredMax,sep="\n") # [3 3 3 1] # عدد التوقعات الصحيحة print("accurately predicted: ",sum(labelMax == PredMax)) # Categorical Accuracy: عدد حالات التطابق على العدد الكلي للتوقعات CAccuracy = sum(PredMax == labelMax)/len(PredMax) print("Categorical Accuracy: ",CAccuracy) # حسابها باستخدام كيراس metric = tf.keras.metrics.CategoricalAccuracy() metric.update_state(label,Pred) metric.result().numpy() """ labelMax: [3 2 2 1] PredMax: [3 3 3 1] accurately predicted: 2 Categorical Accuracy: 0.5 <==>50% 0.5 <==>50% """ هذه الدالة لها الشكل التالي في كيراس: tf.keras.metrics.CategoricalAccuracy(name="categorical_accuracy", dtype=None) ويمكننا استخدامها في نماذجنا مع الدالة compile كالتالي: model.compile( ... metrics=[tf.keras.metrics.CategoricalAccuracy()]) # أو من واجهة كيراس مباشرةً import keras model.compile( ... metrics=[keras.metrics.CategoricalAccuracy()]) # أو بالشكل التالي model.compile( ... metrics=["CategoricalAccuracy"]) انظر للمثال التالي، حيث سأستخدمها مع مسألة تصنيف متعدد: from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=10000) import numpy as np def vectorize_sequences(sequences, dimension=10000): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) from keras.utils.np_utils import to_categorical one_hot_train_labels = to_categorical(train_labels) one_hot_test_labels = to_categorical(test_labels) x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = one_hot_train_labels[:1000] partial_y_train = one_hot_train_labels[1000:] # بناءالنموذج from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=10000) # تررميز البيانات import numpy as np def vectorize_sequences(sequences, dimension=10000): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) from keras.utils.np_utils import to_categorical one_hot_train_labels = to_categorical(train_labels) one_hot_test_labels = to_categorical(test_labels) x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = one_hot_train_labels[:1000] partial_y_train = one_hot_train_labels[1000:] # بناء النموذج from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(64, activation='relu', input_shape=(10000,))) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(46, activation='softmax')) # التجميع model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['CategoricalAccuracy']) # التدريب history = model.fit(partial_x_train, partial_y_train, epochs=6, batch_size=512, validation_data=(x_val, y_val)) """ Epoch 1/6 16/16 [==============================] - 2s 75ms/step - loss: 3.0325 - categorical_accuracy: 0.4249 - val_loss: 1.6946 - val_categorical_accuracy: 0.6590 Epoch 2/6 16/16 [==============================] - 1s 51ms/step - loss: 1.4645 - categorical_accuracy: 0.6999 - val_loss: 1.3093 - val_categorical_accuracy: 0.7150 Epoch 3/6 16/16 [==============================] - 1s 53ms/step - loss: 1.0611 - categorical_accuracy: 0.7740 - val_loss: 1.1516 - val_categorical_accuracy: 0.7480 Epoch 4/6 16/16 [==============================] - 1s 53ms/step - loss: 0.8315 - categorical_accuracy: 0.8172 - val_loss: 1.0494 - val_categorical_accuracy: 0.7790 Epoch 5/6 16/16 [==============================] - 1s 53ms/step - loss: 0.6774 - categorical_accuracy: 0.8535 - val_loss: 0.9816 - val_categorical_accuracy: 0.7860 Epoch 6/6 16/16 [==============================] - 1s 51ms/step - loss: 0.5694 - categorical_accuracy: 0.8753 - val_loss: 0.9275 - val_categorical_accuracy: 0.8000 """

الطريقة الأولى هي استخدام ()numpy.nan و ()numpy.logical_not. فلتكن لدينا المصفوفة التالية: a = numpy.array([2, 8, numpy.nan, 3, 1, numpy.nan]) ولو طبقنا عليها numpy.isnan سوف يعيد لنا نفس المصفوفة لكن بقيم بوليانية بحيث يضع true مكان القيم التي ليست nan و false مكان القيم nan: print(numpy.isnan(a)) # [False False True False False True] الآن لو استخدمنا على الناتج السابق التابع logical_not فسوف يعكس النتائج، أي بدل true سيضع false والعكس: print(numpy.logical_not(numpy.isnan(a))) # [ True True False True True False] الآن يمكننا الاستفادة من الفكرة التالية: e=(np.array([1, 0, 3,4])) e[[True, True, True,False]] # array([1, 0, 3]) لذا يكون الحل كالتالي: import numpy # إنشاؤ المصفوفة a = numpy.array([2, 8, numpy.nan, 3, 1, numpy.nan]) #numpy.logical_not و numpy.isnan(): باستخدام #nan سنقوم بحذف قيم print(numpy.isnan(a)) # [False False True False False True] print(numpy.logical_not(numpy.isnan(a))) # [ True True False True True False] b = a[numpy.logical_not(numpy.isnan(a))] print(b) # [2. 8. 3. 1.] مثال آخر على مصفوفة ثنائية: import numpy # إنشاؤ المصفوفة a = numpy.array([[6, 2, numpy.nan], [2, 6, 1], [numpy.nan, 1, numpy.nan]]) #numpy.logical_not و numpy.isnan(): باستخدام #nan سنقوم بحذف قيم print(numpy.isnan(a)) """ [[False False True] [False False False] [ True False True]] """ print(numpy.logical_not(numpy.isnan(a))) """ [[ True True False] [ True True True] [False True False]] """ b = a[numpy.logical_not(numpy.isnan(a))] print(b) # [6. 2. 2. 6. 1. 1.] أو يمكنك استخدام المعامل ~ بدلاً من logical كالتالي: import numpy a = numpy.array([[12, 5, numpy.nan, 7], [2, 61, 1, numpy.nan], [numpy.nan, 1, numpy.nan, 5]]) a = a[~(numpy.isnan(c))] a #array([12., 5., 7., 2., 61., 1., 1., 5.]) أو من خلال التابع isfinite في نمباي (بنفس المبدأ) : import numpy a = numpy.array([[12, 5, numpy.nan, 7], [2, 61, 1, numpy.nan], [numpy.nan, 1, numpy.nan, 5]]) a[np.isfinite(a)] # array([12., 5., 7., 2., 61., 1., 1., 5.])

del تستخدم مع القوائم وليس مصفوفات نمباي على ما اعتقد، لذالك يظهر الخطأ. هناك عدة طرق للحذف من نمباي، فيمكنك استخدام التابع setdiff1d من نمباي، حيث نمرر له المصفوفة الأصلية والقيم التي نريد حذفها موضوعة ضمن مصفوفة: import numpy as np arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # مصفوفة بالقيم التي نريد حذفها b = np.array([1,2,4]) arr = np.setdiff1d(arr,b) arr # array([3, 5, 6, 7, 8, 9]) أو من خلال التابع delete لكن هنا نمرر له ال index المراد حذفها وليس القيم: import numpy as np arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) b = np.delete(arr, [2,3,6]) #index هنا نمرر له ال b #array([1, 2, 5, 6, 8, 9]) # لحذف عنصر واحد من خلال الفهرس array = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] index = 2 array = np.delete(array, index) array # array([ 10, 20, 40, 50, 60, 70, 80, 90, 100]) أيضاً هنا يتم الحذف من خلال تحديد الفهرس عن طريق استخدام itertools.compress وهي الطريقة الأسرع: import numpy as np arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) import itertools index=[2,3,6] arr = np.array(list(itertools.compress(arr, [i not in index for i in range(len(arr))]))) arr # array([1, 2, 5, 6, 8, 9]) حسناً الطرق السابقة كانت من أجل مصفوفات نمباي، لكن هناك طرق أخرى خاصة بالقوائم، فمثلاً يمكنك تحويل المصفوفة إلى قائمة ثم حذف العنصر من القائمة بإحدى الطرق التالية، ثم إعادة تحويلها لمصفوفة. استخدام Remove لحذف عنصر محدد: array = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] array.remove(40) #[10, 20, 30, 50, 60, 70, 80, 90, 100] أو pop لحذف عنصر من خلال تمرير ال index: array = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] index = 2 array.pop(index) array # [10, 20, 40, 50, 60, 70, 80, 90, 100] أو من خلال del وأيضاً من خلال ال index: array = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] index = 2 del array[index] array # [10, 20, 40, 50, 60, 70, 80, 90, 100]

من كيراس باستخدام التابع to_categorical import numpy as np a = np.array([1, 0, 3]) from keras.utils.np_utils import to_categorical one_hot_train = to_categorical(a) one_hot_train """ array([[0., 1., 0., 0.], [1., 0., 0., 0.], [0., 0., 0., 1.]], dtype=float32) """ أو يمكنك القيام بذلك من خلال تشكيل تابع: import numpy as np a = np.array([1, 0, 3]) # dimension: أكبر عنصر في بياناتك+1 def vectorize_sequences(sequences, dimension=a[max(a)]+1): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results OneHOT = vectorize_sequences(a) OneHOT """ array([[0., 1., 0., 0.], [1., 0., 0., 0.], [0., 0., 0., 1.]]) """ أيضاً بشكل يدوي من خلال استخدام عدة توابع في نمباي : import numpy as np a = np.array([1, 0, 3]) b = np.zeros((a.size, a.max()+1)) b[np.arange(a.size),a] = 1 b أيضاً طريقة أخرى، عبر الاستعانة بتوابع نمباي: import numpy as np a = np.array([1, 0, 3]) def one_hot(a, dimension=a[max(a)]+1): return np.squeeze(np.eye(dimension)[a.reshape(-1)]) one_hot(a) """ array([[0., 1., 0., 0.], [1., 0., 0., 0.], [0., 0., 0., 1.]]) """ يمكنك أيضاً استخدام مكتبة باندا من خلال التابع get_dummies: import numpy as np import pandas a = np.array([1, 0, 3]) one_hot_encode=pandas.get_dummies(a) one_hot_encode """ 0 1 3 0 0 1 0 1 1 0 0 2 0 0 1 """ أو من مكتبة sklearn استخدام التابع OneHotEncoder: import numpy as np import pandas a = np.array([1, 0, 3]) from sklearn.preprocessing import OneHotEncoder enc = OneHotEncoder(handle_unknown='ignore') o=enc.fit_transform(a.reshape(-1, 1)) onehot=o.toarray() onehot """ array([[0., 1., 0.], [1., 0., 0.], [0., 0., 1.]]) """ لكن في آخر طلريقتين سيكون حجم الشعاع لكل قيمة يساوي عدد العناصر المختلفة. أي لن يقوم بعملية تمثيلهم حسب ال index انظر: import numpy as np import pandas a = np.array([1, 0, 4]) from sklearn.preprocessing import OneHotEncoder enc = OneHotEncoder() one_hot = enc.fit_transform(a.reshape(-1, 1)) one_hot.toarray() """ array([[0., 1., 0.], [1., 0., 0.], [0., 0., 1.]]) """

تقوم هذه الدالة بحساب مدى دقة النموذج، وتستخدم مع مهام التصنيف الثنائي، وتختلف عن مقياس الدقة accuracy (يمكنك الاطلاع عليها من الرابط في الأسفل) في أنها تسمح لنا بتحديد عتبة للتوقع أي ال "threshold" أي تعطينا قدرة أكبر في التحكم بعملية التوقع، وترد هذه الدالة قيمة عشرية بين 0 و 1 بحيث كلما اقتربت القيمة من 1 كانت دقة النموذج أعلى. وتماماً كما في الدالة Accuracy تقوم هذه الدالة بحساب عدد المرات التي قام فيها نموذجنا بتوقع القيم بشكل صحيح (عدد مرات الإصابة في التنبؤ أو بمعنى آخر عدد مرات التطابق) وتقسمها على عدد التوقعات الكلية (الصحيحة والخاطئة أي حالات التطابق وعدم التطابق). والمثال التالي سيوضح كل شيء، حيث قمت في البداية بكتابة كود بشكل يدوي لتحقيق هذا التابع ثم استخدمت كيراس: import numpy as np import tensorflow as tf # إنشاء مصفوفتين واحدة تمثل القيم المتوقعة والأخرى الحقيقية yTrue = np.array([[1],[0],[0],[1],[1]]) print("yTrue: ",yTrue,sep="\n") Pred = np.array([[0.6],[0.2],[0.4],[0.95],[1.0]]) print("Pred: ",Pred,sep="\n") Threshold = 0.5 # تابع لمدا لتعيين 1 في حالة كانت القيمة المتوقعة أكبر من العتبة و0 إذا كانت أقل منها pM = lambda x : 0 if x <= Threshold else 1 # تطبيق التابع السابق على كل العينات yPred = Pred.astype(int) for i in range(len(yPred)): yPred[i] = pM(Pred[i]) print("predicted values: ",yPred,sep="\n") print("accurately predicted : ",sum(yPred == yTrue),sep="\n") print("len: ",len(yPred)) # الآن نقوم بقسمة عدد العينات التي تم توقعها بشكل صحيح على العدد الكلي للعينات BinaryAccuracy = sum(yPred == yTrue)/len(yPred) # باستخدام كيراس Binary Accuracy حساب metric = tf.keras.metrics.BinaryAccuracy(threshold = Threshold) metric.update_state(yTrue,yPred) metric.result().numpy() """ yTrue: [[1] [0] [0] [1] [1]] Pred: [[0.6 ] [0.2 ] [0.4 ] [0.95] [1. ]] predicted values: [[1] [0] [0] [1] [1]] accurately predicted : [5] len: 5 1.0 # 100% """ هذه الدالة لها الشكل التالي في كيراس: tf.keras.metrics.BinaryAccuracy( name="binary_accuracy", dtype=None, threshold=0.5 ) # threshold هي العتبة ويمكننا استخدامها في نماذجنا مع الدالة compile كالتالي: model.compile(optimizer='sgd', loss='mse', metrics=[tf.keras.metrics.BinaryAccuracy()]) # أو model.compile(optimizer='sgd', loss='mse', metrics=["BinaryAccuracy"]) انظر للمثال التالي، حيث سأستخدمها مع مسألة تصنيف ثنائي: from keras.layers import Embedding from keras.datasets import imdb from keras import preprocessing max_features = 10000 maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) x_train = preprocessing.sequence.pad_sequences(x_train, maxlen=maxlen) x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) from keras.models import Sequential from keras.layers import Flatten, Dense model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['BinaryAccuracy']) model.summary() history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2)

هناك عدة طرق أولها استخدام التابع unique ثم zip كالتالي: import numpy as np a = np.array([1,1,1,2,2,2,5,25,1,1]) unique, counts = np.unique(a, return_counts=True) dict(zip(unique, counts)) # {1: 5, 2: 3, 5: 1, 25: 1} أو من خلال التابع Counter كالتالي : import numpy as np a = np.array([1,1,1,2,2,2,5,25,1,1]) import collections collections.Counter(a) # Counter({1: 5, 2: 3, 5: 1, 25: 1}) أو باستخدام bincount وهي الطريقة الأسرع، حيث تقوم هذه الطريقة بإعادة مصفوفة طولها بطول أكبر قيمة في مصفوفتك، أي إذا كانت 30 سيكون خرجها شعاع ب 30 عنصر بحيث كل index فيها يقابل تكرار الرقم الموافق له في بياناتك، أي مثلاً ال index رقم 1 في مصفوفة الخرج يقابل عدد مرات ظهور الرقم 1 في مصفوفتك: import numpy as np a = np.array([1,1,1,2,2,2,5,25,1,1]) print(np.bincount(a)) """ [0 5 3 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1] """ أو من خلالscipy.stats.itemfreq : import numpy as np a = np.array([1,1,1,2,2,2,5,25,1,1]) from scipy.stats import itemfreq itemfreq(a) """ array([[ 1, 5], [ 2, 3], [ 5, 1], [25, 1]]) """ وآخر حل من خلال pandas مع التابع stack من نمباي، كالتالي: import numpy as np a = np.array([1,1,1,2,2,2,5,25,1,1]) import pandas as pd def pandas_value_counts(a): out = pd.value_counts(pd.Series(a)) out.sort_index(inplace=True) out = np.stack([out.keys().values, out.values]).T return out pandas_value_counts(a) """ array([[ 1, 5], [ 2, 3], [ 5, 1], [25, 1]]) """

أبسط طريقة: # نحدد الأبعاد والقيمة np.full((4, 3), 2, dtype=int) """ array([[2, 2, 2], [2, 2, 2], [2, 2, 2], [2, 2, 2]]) """ وهناك طرق عديدة أخرى سأعرضها في المثال بعد قليل، لكن قبل ذلك أود أن ألفت الانتباه إلى أن الدالة repeat نمرر لها القيمة ثم عدد المرات التي نريد بها تكرار هذه القيمة ، وبالتالي تعيد لنا مصفوفة ببعد واحد، وبالتالي يمكننا تغيير أبعاد المصفوفة الناتجة حسبما نريد باستخدام التابع reshape، فمثلاً نريد إنشاء مصفوفة بأبعاد 5*5 وكل قيمها 4، وبالتالي نقوم باستتدعاء الدالة repeat بالشكل التالي repeat(4,25) ثم نقوم بعمل إعادة تعيين للأبعاد أي تصبح بالشكل التالي: np.repeat(4,25).reshape(5,5) وبنفس الطريقة يمكننا استخدام التابع array مع reshape لتحقيق مانريده. أي يمكنك استخدام الدالة reshape لتحويل مصفوفتك إلى أي شكل لكن تذكر أن عدد العناصر قبل التحويل يجب أن يساوي عدد العناصر بعد التحويل أي في المثال السابق كان لدينا مصفوفة ب 25 قيمة وبالتالي لايمكنك تحويلها لمصفوفة بأبعاد 3*4 لأن 3*4=12 عنصر أي لاتساوي 25. # الهدف إنشاء مصفوفة بأبعاد 5*5 وكل القيم 4 a=np.repeat(4,25) # 1D array """ array([4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4]) """ a=a.reshape(5,5) """ array([[4, 4, 4, 4, 4], [4, 4, 4, 4, 4], [4, 4, 4, 4, 4], [4, 4, 4, 4, 4], [4, 4, 4, 4, 4]]) """ # اختصاراً np.repeat(4,25).reshape(5,5) المثال التالي يوضح كل شيئ: #fill ثم التابع empty استخدام الدالة a=np.empty((3,3)); a.fill(5) """ array([[5., 5., 5.], [5., 5., 5.], [5., 5., 5.]]) """ # أيضاً استخدام نفس التابع لكن بشكل مختلف a=np.empty((3,3)); a[:]=5 # نقوم بإسناد القيمة التي نريدها لكل عناصر المصفوفة #ones من خلال التابع a=np.ones((3,3))*5 """ array([[5., 5., 5.], [5., 5., 5.], [5., 5., 5.]]) """ #repeat من خلال التابع a=np.repeat(5,9).reshape(3,3) a """ array([[5, 5, 5], [5, 5, 5], [5, 5, 5]]) """ # numpy.tile(v, (rows,cols)) a=np.tile(5,(3,3)) a """ array([[5, 5, 5], [5, 5, 5], [5, 5, 5]]) """ #reshape التابع repeatسنستخدم بنفس فكرة a=np.array(9 * [5]).reshape(3,3) """ array([[5, 5, 5], [5, 5, 5], [5, 5, 5]]) """ وأسر ع طريقة هي استخدام الدالة empty

numpy.array هي تابع يعيد numpy.ndarray لكن لايوجد نمط بيانات من نوع numpy.array ، للتوضيح انظر للمثال التالي: a=[2,4,4] # list #numpy.ndarray لاحظ أنه عبارة عن تابع نمرر له نمط بيانات كالقوائم ويرد لنا a = np.array(a) type(a) # numpy.ndarray print(type(a)) # <class 'numpy.ndarray'> # أو لو جربت isinstance(a, (np.ndarray)) # True سيعطيك أي من السطرين التاليين رسالة خطأ: np.ndarray(a) # error #np.array(a) يجب أن يكون isinstance(a, (np.array)) #error # يجب أن يكون isinstance(a, (np.ndarray)) أي باختصار numpy.ndarray هي نمط بيانات في بايثون أما numpy.array هي تابع يقوم بتحويل الدخل إلى النمط numpy.ndarray

التابع predict يقوم فقط بتمرير بيانات الدخل إلى النموذج فتحصل على الخرج (القيمة المتوقعة بناءان على أوزان التدريب التي تم حفظها في الملفات). لذا لايعطيك أي مشكلة. أما عند استخدام evaluate ، فهذا التابع يقوم بحساب الخطأ loss و ال metrics، ودالة التكلفة التي نحسب من خلالها ال loss لايكون لدينا معلومات عنها حتى تقوم بتجميع النموذج compile. فهم وسطاء لتابع ال compile: model.compile(optimizer=.., loss=.., metrics=..) إن كل مايهمنا من تدريب النموذج هو استخلاص الأوزان المدربة: إن مخرجات النموذج النهائية هي عبارة عن أوزان هذه الأوزان تكون مدربة لتنفيذ المهمة التي قمنا بتدريبها من أجل حلها، في البداية نقوم بتهيئتها بقيم عشوائية (بين ال 0 و 1). ثم عن طريق النموذج الذي بنيناه وعن طريق خوارزمية Backbropagation يتم تحديث قيم هذه الأوزان (تدريبها لحل المشكلة)، وبعد انتهاء التدريب نقوم بإدخال العينة التي نريد تجربتها أو اختبار الأداء عليها، فيحسب النموذج الناتج لنا بناءان على قيم هذه الأوزان. وهذا هو كل ما يهمنا (بناء نموذج قادر عتلى تصنيف الصور مثلاً بحيث نعطيه صورة ويعطينا الخرج أما التفاصيل الأخرى لاتهمنا كمستخدمين). حسناً إن التكلفة "loss" هي دالة نقوم باستخدامها خلال عملية التدريب حيث تستلم هذه الدالة القيم المتوقعة من النموذج والقيم الحقيقية ثم تقارنهما وتعطي قيمة تعبر عن مدى اختلاف القيمتين (الفرق بينهما). وطبعاً يكون الهدف هو تصغير قيمة التكلفة (الخطأ) لأنه كلما قل الاختلاف بين القيم التي يتوقعها النموذج والقيم الحقيقية يصبح نموذجك أفضل. إذاً ال loss ليست مفيدة للغرض النهائي للنموذج، لكنها ضرورية للتدريب. وهذا هو السبب في أنه يمكنك الحصول على توقعات من النموذج لكن دون ال loss. لكن إذا أردت لسبب ما أن تحسب ال loss أيضاً فيجب عليك تنفيذ ال compile لنموذجك، انظر للمثال التالي الذي سأقوم فيه بحفظ نموذج ثم سأعيد تحميله وأنفذ عليه التابع evaluate: from keras.models import Sequential from keras.layers import Dense from keras.models import model_from_yaml import numpy import os dataset = numpy.loadtxt("pima-indians-diabetes.csv", delimiter=",") X = dataset[:,0:8] Y = dataset[:,8] # بناء النموذج model = Sequential() model.add(Dense(16, input_dim=8, activation='tanh')) model.add(Dense(1, activation='sigmoid')) # تجميع النموذج model.compile(loss='binary_crossentropy', optimizer='rmsprop', metrics=['acc']) # تدريب النموذج model.fit(X, Y, epochs=120, batch_size=10, verbose=0) # تقييم النموذج scores = model.evaluate(X, Y, verbose=0) print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100)) # acc: 78.78% # حفظه model_j = model.to_json() with open("model.json", "w") as f: f.write(model_j) model.save_weights("model.h5") # الآن إعادة تحميله json_file = open('model.json', 'r') loaded_model_json = json_file.read() json_file.close() model = model_from_json(loaded_model_json) # تحمبل الأوزان model.load_weights("model.h5") #نقوم الآن بتجميع النموذج model.compile(loss='binary_crossentropy', optimizer='rmsprop', metrics=['acc']) # قم بتحديد دالة التكلفة والمعيار # على بيانات الاختبار evaluate score = model.evaluate(X, Y, verbose=0) # حساب ال loss print('Test loss:', score[0]) #metrics حساب ال print('Test accuracy:', score[1])

استخدامك للتضمين هنا غير صحيح ، فعندما تكون مدخلاتك لها قيم سلبية، يكون الترميز غير صالح لاستخدام مع طبقة التضمين، يحب أن يكون ترميز الكلمات في المستندات عبارة عن أعداد صحيحة موجبة حصراً (كل كلمة فريدة يتم ربطها بعدد صحيح يمثلها). حيث أن طبقة التضمين هي طبقة تتيح لنا تحويل كل كلمة إلى متجه بطول ثابت وبحجم محدد. المتجه الناتج هو متجه كثيف "Dense" له قيم حقيقية بدلاً من 0 و 1 فقط كما في الترميز One-Hot. يساعدنا الطول الثابت لمتجهات الكلمات على تمثيل الكلمات بطريقة أفضل وأكثر فعالية مع أبعاد مخفضة. وهذه المتجهات تكون ممثلة في فضاء Vector space مهيكل ويعكس المعاني الدلالية لكل كلمة. ويمكن اعتبارها كقاموس يقوم بربط أعداد صحيحة (كل كلمة ترمز في البداية كعدد صحيح) بمتجه كثيف. أي أنها تأخذ كدخل أعداد صحيحة ثم تبحث في هذا القاموس على المتجه الذي يقابله في القاموس الداخلي، ويعيد هذا القاموس. Word index --> Embedding layer --> Corresponding word vector إذا كون مدخلاتك تحوي أعداداً سلبية يعني أن استخدام التضمين غير صحيح هنا. إن التضمين يعمل مع أي نوع من مدخلات الأعداد الصحيحة الموجبة، ولكن ليس مع المدخلات العامة.

المصفوفات التي تريد ربطها يجب أن يتم تمريرها على شكل sequence وليس كما قمت بتمريرهم على شكل وسيطين منفصلين كالتالي: import numpy a = numpy.array([1, 2, 3]) b = numpy.array([5, 6]) numpy.concatenate([a,b],axis=0) # array([1, 2, 3, 5, 6]) # أو numpy.concatenate((a,b)) # array([1, 2, 3, 5, 6]) وهناك طرق أخرى لربط المصفوفات أحادية البعد مثل numpy.r_ وnumpy.hstack : import numpy a = numpy.array([1, 2, 3]) b = numpy.array([5, 6]) numpy.r_[a, b] # array([1, 2, 3, 5, 6]) numpy.hstack([a, a]) # array([1, 2, 3, 1, 2, 3]) لكن غالباً الخيار الأفضل والأكثر سهولة هو concatenate لذا الآن دعنا نتعلم أكثر عنه: يمكن استخدام الدالة concatenate في NumPy لربط مصفوفتين إما على مستوى الصف "row-wise" أي يمعنى (axis=0) أو على مستوى العمود "column-wise". يمكن أن تأخذ الدالة concatenate مصفوفتين أو أكثر ، وافتراضياً تقوم بربطهم على أساس الأسطر ، أي المحور = 0: # concatenate 2 numpy arrays: row-wise import numpy as np array = np.arange(4) arr1 = array.reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,8).reshape(2,2) """ array([[4, 5], [6, 7]]) """ np.concatenate((arr1, arr2)) """ array([[0, 1], [2, 3], [4, 5], [6, 7]]) """ أما بالنسبة للأعمدة: # concatenate 2 numpy arrays: column-wise import numpy as np array = np.arange(4) arr1 = array.reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,8).reshape(2,2) """ array([[4, 5], [6, 7]]) """ np.concatenate((arr1,arr2),axis=1) """ array([[0, 1, 4, 5], [2, 3, 6, 7]]) """ ويمكنك ربط أكثر من مصفوفة: # concatenate 2 numpy arrays: column-wise import numpy as np array = np.arange(4) arr1 = array.reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,8).reshape(2,2) """ array([[4, 5], [6, 7]]) """ np.concatenate((arr1,arr2,arr1),axis=1) """ array([[0, 1, 4, 5, 0, 1], [2, 3, 6, 7, 2, 3]]) """ np.concatenate((arr1,arr2,arr1),axis=0) """ array([[0, 1], [2, 3], [4, 5], [6, 7], [0, 1], [2, 3]]) """ لكن تذكر أن الأبعاد يجب أن تكون صحيحة أي مثلاً لربط مصفوفتين على المحور 1، يجب أن يكون لكل من المصفوفتين نفس عدد الأسطر، أما بالنسبة للأسطر فيجب أن تتطابق أبعاد الأعمدة: ######################################## هنا سيعمل ######## import numpy as np arr1 = np.arange(4).reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,6).reshape(2,1) """ array([[4], [5]]) """ np.concatenate((arr1,arr2),axis=1) """ array([[0, 1, 4], [2, 3, 5]]) """ ######################################### لكن هنا لن يعمل لعدم إمكانية مطابقةالأبعاد######### arr2 = np.arange(4,6).reshape(1,2) # يجب أن تتطابق أبعاد الأعمدة #array([[4, 5]]) np.concatenate((arr1,arr2),axis=1) @ ValueError: all the input array dimensions for the concatenation axis must match exactly, but along dimension 0, the array at index 0 has size 2 and the array at index 1 has size 1 أيضاً لربط المصفوفات يمكننا استخدام vstack وهي تكافئ concatenate عندما يكون المحور =0 حيث تقوم بتكديس المصفوفات عمودياً أي row wise: import numpy as np arr1 = np.arange(4).reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,6).reshape(1,2) # الأبعاد الأفقية يجب أن تطابق عند التكديس العمودي """ array([[4], [5]]) """ np.vstack((arr1, arr2)) """ array([[0, 1], [2, 3], [4, 5]]) """ أما hstack فهي مثل concate أيضاً لكن تستخدم لتكديس المصفوفات أفقياً: import numpy as np arr1 = np.arange(4).reshape((2,2)) """ array([[0, 1], [2, 3]]) """ arr2 = np.arange(4,6).reshape(2,1) # ركز """ array([[4], [5]]) """ np.hstack ((arr1, arr2)) """ array([[0, 1, 4], [2, 3, 5]]) """

الدالة flatten دوماً تعيد نسخة أي "copy". أما ravel فيقوم بإرجاع view (طريقة أخرى لعرض بيانات المصفوفة. وتعني أنه يتم مشاركة بيانات كلا الكائنين.) للمصفوفة الأصلية كلما أمكن ذلك. وهذا يكون غير مرئي في الإخراج الذي يتم طباعته، لكن إذا قمت بتعديل المصفوفة التي تم إرجاعها بواسطة رافيل، فسيتم التعديل أيضاً في المصفوفة الأصلية. أما إذا قمت بذلك في flatten فلن يحدث ذلك. غالبًا ما يكون ravel أسرع نظرًا لعدم نسخ ذاكرة ، ولكن عليك أن تكون أكثر حذراً بشأن تعديل المصفوفة التي تعيدها. انظر للمثال التالي الذي يوضح الأمر: import numpy as np y = np.arange(9).reshape(-1,3) """array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])""" e=y.flatten() # array([0, 1, 2, 3, 4, 5, 6, 7, 8]) a=y.ravel() # array([0, 1, 2, 3, 4, 5, 6, 7, 8]) a[0]=144 print(a) # [144 1 2 3 4 5 6 7 8] print(y) """ [[144 1 2] [ 3 4 5] [ 6 7 8]] """ e[2]=88 print(e) # [ 0 1 88 3 4 5 6 7 8] print(y) # لاحظ كيف لم ينتقل التعديل """ [[144 1 2] [ 3 4 5] [ 6 7 8]] """

يمكنك القيام بذلك بالشكل التالي من خلال scipy: import scipy.misc scipy.misc.imsave('outfile.jpg', image_array) أو من خلال مكتبة PIL : from PIL import Image im = Image.fromarray(A) im.save("your_file.jpeg") أو من خلال مكتبة matplotlib : import matplotlib matplotlib.image.imsave('name.png', array) ومن خلال مكتبة png لكن قم أولاً بتحميل المكتبات : # pip install pypng # python setup.py install import png png.from_array([[255, 255, 122, 255], [0, 255, 255, 0]], 'L').save("im.png") أو من خلال مكتبة opencv: import cv2 img = ... # مصفوفتك cv2.imwrite("filename.png", img) # المسار والصورة

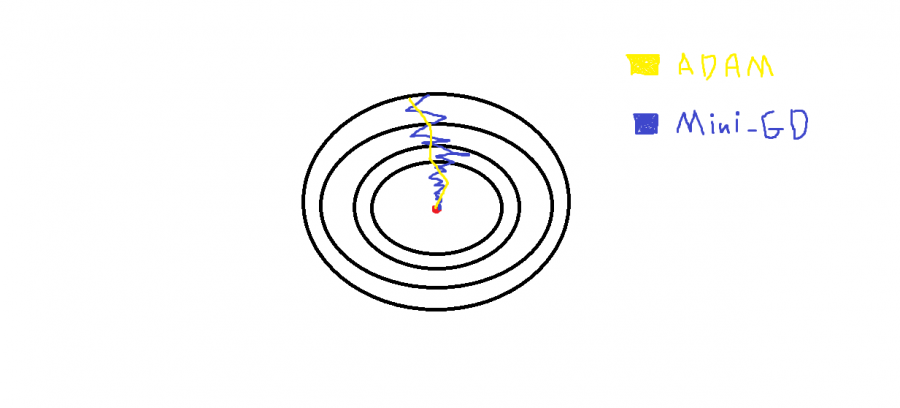
باختصار هذه الخوارزمية تقوم بتسريع أداء نموذجك (أي تجعله يتقارب إلى القيم الصغرى الشاملة لل Cost Function بشكل أسرع وأدق) أي أنها تحسين لخوارزمية الGD بأنواعها المختلفة Batch-GD و Mini-Batch GD و Stocastic GD ففي هذه الخوارزميات ولاسيما الميني والستوكاستيك يكون مسار التدرج إلى القيمة الصغرى الشاملة متعرجاً (متذبذباً أي اتجاهه ليس بشكل مباشر إلى القيمة الصغرى) وبالتالي يكون النموذج أبطأ وأقل دقة. أما ADAM فهو تحسين ل GD حيث يستخدم فكرة ال Exponentially wighted average ويطبقها في عملية تحديث الأوزان التدريبية وبالتالي تصبح التدرجات gredients أو قيم المشتقات معتمدة على قيم المشتقات السابقة مما يجعل المسار العام للتدرجات أفضل وتخفف من التذبذبات في مسار خوارزمية ال GD، انظر للشكل التالي الذي يوضح كلامي: حيث أن النقطة الحمراء تشير إلى القيمة الصغرى الشاملة GM لدالة التكلفة، لاحظ كيف أن آدم يقوم بجعل المسار موجه مباشرة (يخفف التعرجات) إلى القيمة GM، وبشكل أكثر تفصيلاً: هي اختصار ل Adaptive moment estimation، وتقوم فكرة خوارزمية التحسين هذه على دمج خوارزمية التحسين RMSprop مع خوارزمية التحسين Momentum أي تجمع بينهما، ويعتبر هذه المحسن إلى جانب RMSprop أفضل خوارزميات التحسين الموجودة ويناسبان أغلب المشاكل "المصدر آندرو ج" و "فرانسوا كوليت"، حيث تعتمد على نفس أفكار الخوارزميتين السابقتين (حساب ال Exponentially wighted average للمشتقات السابقة (المتوسطات الأسية)) لكنها تضيف لهم فكرة ال bias correction وبالتالي تعطي تحسن أكبر في المراحل الابتدائية للتدريب. وبشكل عام لايهمك الخوض كثيراً في تفاصيلها فكيراس وتنسرفلو يجعلان استخدامها بسيطاً: keras.optimizers.Adam( learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False, name="Adam", **kwargs ) الوسيط الأول هو معامل التعلم (حجم الخطوة)، الوسيط الثاني أي beta1 هو الوسيط الخاص بال momentum أما الوسيط الثالث فهو قيمة بيتا الخاصة ب RMSprop ولا أنصحك بتغيير قيمتهما فهما القيمتين المثاليتين في 95% من الحالات. الوسيط الرابع هو epsilon وهي قيمة تستخدم مع المومينتوم وال ار ام اس بروب وتستخدم من أجل منع حصول القسمة على صفر (هذه انسى أمرها لاتهمنا في أي شيئ) لكن أنصحك بتغيير القيمة الافتراضية إلى الأس 8 أو 9 بدلاً من الأس 7 لأسباب رياضية بحتة. والوسيط الأخير لتحديد فيما ما إذا كان سيتم تطبيق متغير AMSGrad لهذه الخوارزمية من الورقة البحثية التي صدرت عام 2018 بعنوان "On the Convergence of Adam and beyond" أم لا (هي تحسين على adam) ولاستخدامها مع نماذجك يمكنك القيام بذلك ببساطة من خلال تمريرها للدالة compile، بالشكال التالي: model.compile( optimizer=keras.optimizers.Adam( learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False, name="Adam", ) # أو model.compile( optimizer="Adam" ) انظر للنموذج البسيط التالي، حيث استخدمها في مهمة NLP لتحليل مراجعات الأفلام على مجموعة بيانات IMDB: from keras.datasets import imdb from keras import preprocessing import keras max_features = 1000 maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) x_train = preprocessing.sequence.pad_sequences(x_train,maxlen=maxlen) x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) from keras.models import Sequential from keras.layers import Dense model = Sequential() model =Sequential() model.add(Dense(16, activation='relu',input_shape=(20,))) model.add(Dense(16, activation='relu')) model.add(Dense(1, activation='sigmoid')) model.compile(optimizer=keras.optimizers.Adam( learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=True, name="Adam", ) , loss='binary_crossentropy', metrics=['acc']) history = model.fit(x_train, y_train, epochs=3, batch_size=64, validation_split=0.2)

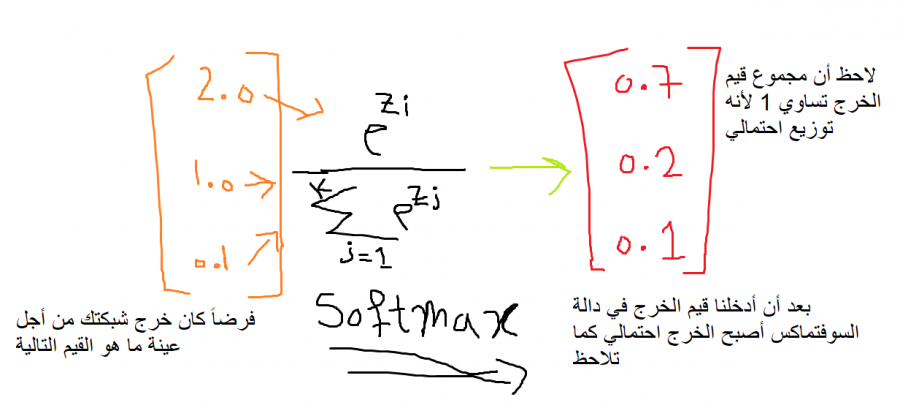
هي دالة رياضية نستخدمها كدالة تنشيط، مدخلاتها شعاع من الأعداد، وخرجها شعاع من القيم الاحتمالية، أي تقوم بتحويل متجه الأعداد إلى متجه احتمالي، حيث تتناسب احتمالات كل قيمة مع المقياس النسبي لكل قيمة في المتجه. ونستخدمها لمهام التصنيف المتعدد، حيث نضعها في آخر طبقة. ولها الشكل التالي: أي تأخذ كل قيمة من قيم شعاع الدخل على حدى، ثم تقوم بحساب ال exp لهذا العدد ثم تقسم الناتج على المجموع الكلي لل exp لكل العينات (وبالتالي الخرج سيكون عبارة عن توزيع احتمالي). ولفهم هذا الكلام أكثر لنأخذ المثال التالي، لدينا 3 أصناف من الكرات (x,y,z) بما أنه لدينا 3 أصناف وبالتالي خرج الشبكة يجب أن يكون 3 قيم (أي يجب أن يكون لديك 3 خلايا في الخرج) بحيث كل قيمة تعبر عن احتمالية أن العينة هي إحدى الأصناف، حسناً لنرمز ل x ب 0 و y ب 1 و z ب 2 وبالتالي يمكن تمثيلها ك One-hot بالشكل التالي : x0=[1,0,0] y0=[0,1,0] z0=[0,0,1] ونحن لدينا 3 عصبونات في آخر طبقة، وبالتالي سيمثل العصبون الأول احتمالية كون العينة (الكرة) تمثل الصنف x، والعصبون الثاني احتمالية كون العينة (الكرة) تمثل الصنف y، والعصبون الأخير احتمالية كون العينة تنتمي للصنف z. فمثلاً من أجل عينة ما، عند الوصول لآخر طبقة سيتم إدخال ناتج آخر طبقة ( هنا شعاع من 3 قيم) إلى هذا التابع وبالتالي يصبح الخرج احتمالياً كما يلي: طبعاً القيم الاحتمالية التي وضعتها بشكل تقديري، لكن حتماً سيكون المجموع1، الآن سأكتب لك إياها بكود بسيط: # transform values into probabilities from math import exp # calculate each probability summation=(exp(7.0) + exp(2.0) + exp(0.1)) p1 = exp(7.0) / summation p2 = exp(2.0) / summation p3 = exp(0.1) / summation print(p1, p2, p3) # 0.9923138027987766 0.006686157809719105 0.0010000393915043245 # sum of probabilities print(p1 + p2 + p3) # 1.0 انظر كيف سأقوم بتحقيق هذا التابع، وسأطبقه على نفس السؤال: from numpy import exp def softmax(vector): e = exp(vector) return e / e.sum() # define data data = [7.0, 2.0, 0.1] # التحويل result = softmax(data) print(result) # probabilities # [0.9923138 0.00668616 0.00100004] في كيراس وتنسرفلو تتواجد في الموديول التالي (لاحظ أنه موجود ضمن موديول الطبقات): tf.keras.layers.Softmax() ويمكنك تمريرها لنموذجك كدالة تنشيط في آخر طبقة عندما تكون المهمة مهمة تصنيف، كما في المثال التالي، حيث أنه لدينا مهمة تصنيف متعدد ل 46 صنف: from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=10000) # ترميز البيانات import numpy as np def vectorize_sequences(sequences, dimension=10000): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) from keras.utils.np_utils import to_categorical one_hot_train_labels = to_categorical(train_labels) one_hot_test_labels = to_categorical(test_labels) # بناء النموذج from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(64, activation='relu', input_shape=(10000,))) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(46, activation='softmax')) # هنا الطبقةالأخيرة model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy']) # التدريب x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = one_hot_train_labels[:1000] partial_y_train = one_hot_train_labels[1000:] history = model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val)) وللتنويه يمكنك أيضاً استخدامها في الطبقات الخفية لكنها لن تعطيك نتائج مقبولة، مقارنة بالدوال الأخرى (استخدمها فقط كدالة تنشيط في الطبقة الأخيرة).

عندما نريد إعادة تعيين حجم مصفوفة فإننا نقوم باستخدام هذا التابع، مثلاً إذا كانت لديك مصفوفة أحادية ل 20 عنصر يمكنك تحويلها لثنائية لكن يجب أن يكون عدد الأسطر * عدد الأعمدة يساوي 20 وبالتالي نمرر له البعد الأول والثاني اللذين نريد إعادة تعيين أبعاد المصفوفة إليهما، مثلا 5 و 4 أو 10 و 2 حيث أن جداءهما يساوي 20، لكن للاختصار يمكننا أن نمرر البعد الأول او الثاني فقط و البعد الآخر نضع بدلاً منه --1 وبالتالي يفهمها بايثون ويستنتج البعد الآخر من تلقاء نفسه، انظر للأمثلة التالية: arr=np.arange(20) arr.shape # (20,) # هنا أعطى خطأ لأن جداء الأسطر بالأعمدة يجب أن يساوي حجم المصفوفة الأصلية #arr.reshape(10,5) # ValueError: cannot reshape array of size 20 into shape (10,5) arr.reshape(10,2) # (10,2) arr.reshape(2,10) # (2,10) arr.reshape(4,5) # (4,5) # هنا سيستنتج البعد الآخر بناءان على فكرة أن الجداء يجب أن يساوي أبعاد المصفوفة الأصلية arr.reshape(-1,2) # (10,2) arr.reshape(-1,10) # (2,10) arr.reshape(4,-1) #(4,5) # أعطى هنا خطأ لأنه لايوجد عدد تضربه ب6 يعطيك 20 arr.reshape(6,-1) # ValueError: cannot reshape array of size 20 into shape (6,newaxis)

بالشكل التالي: pd.DataFrame(data=data[1:,1:], # القيم index=data[1:,0], # العمودالأول كفهرس columns=data[0,1:]) # الصف الأول كأسماء الأعمدة حيث تحتاج إلى تحديد ال data والفهرس والأعمدة إلى باني ال dataframe: import numpy as np data = np.array([ ['', 'Col1', 'Col2'], ['Row1', 1, 2], ['Row2', 3, 4] ]) import pandas as pd pd.DataFrame(data=data[1:,1:], # القيم index=data[1:,0], # العمودالأول كفهرس columns=data[0,1:]) # الصف الأول كأسماء للأعمدة """ Col1 Col2 Row1 1 2 Row2 3 4 """ حيث أن: data[1:,1:] """ array([['1', '2'], ['3', '4']], dtype='<U4') """ data[1:,0] """ array(['Row1', 'Row2'], dtype='<U4') """ data[0,1:] """ array(['Col1', 'Col2'], dtype='<U4') """ ويمكنك أيضاً أن تقوم بتغيير نمط البيانات الخاص بالقيم إذا أردت بالشكل: import numpy as np data = np.array([ ['', 'Col1', 'Col2'], ['Row1', 1, 2], ['Row2', 3, 4] ]) import pandas as pd pd.DataFrame(data=np.int_(data[1:,1:]), # القيم index=data[1:,0], # العمودالأول كفهرس columns=data[0,1:]) # الصف الأول كأسماء الأعمدة """ Col1 Col2 Row1 1 2 Row2 3 4 """

يمكنك استخدام الدالة astype بالشكل التالي: import numpy as np arr = np.array((0.2,1.7, 4.2, -1.2)) # array([ 0.2, 1.7, 4.2, -1.2]) arr = arr.astype(int) arr # array([ 0, 1, 4, -1])