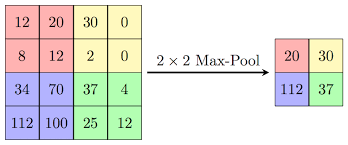Ali Haidar Ahmad

يجب عليك أولاً أن تقوم باستيراد الطبقات قبل استخدامها، ومشكلتك هي أنك لم تقم باستيراد الطبقة Dense. فظهر لك هذا الخطأ، وبالتالي يجب أن تضيف إلى نموذجك السطر التالي، من Keras API حيث أنها موجودة في الموديول: keras.layers.Dense # وبالتالي نكتب from keras.layers import Dense أو من تنسرفلو حيث تكون في الموديول التالي: tensorflow.keras.layers.Dense from tensorflow.keras.layers import Dense ويمكنك استيراد أي طبقة أخرى بنفس الطريقة، مثلاً نريد أن نقوم باستيراد ال'طبقة LSTM أو GRU أو conv..إلخ: # نكتب from keras.layers import Conv2D,LSTM,GRU # أو from tensorflow.layers import Conv2D,LSTM,GRU # أو import tensorflow as tf from tf.layers import Conv2D,LSTM,GRU # أو import tensorflow.layers as layers from layers import Conv2D,LSTM,GRU

عند بناء النماذج، يجب أن تقوم دوماً بتحديد حجم الإدخال الذي ستتعامل معه شبكتك، وأنت هنا لم تقم بتحديده فظهرت المشكلة. حقيقةً وبشكل عام، عند بناء الشبكات العصبية ينبغي علينا تحديد حجم الدخل لكل طبقة لكن كيراس تغنيك عن ذلك فيكفي أن تعطيها حجم الإدخال لأول طبقة وهي ستستنتج حجم الإدخال لباقي الطبقات. حسناً أنت تتعامل مع مهمة NLP ولديك بيانات كل عينة فيها عبارة عن مستند نصي مؤلف من عدد مختلف من الكلمات،وكونك قمت بتحميلها من كيراس فهي تكون مرمزة بأعداد صحيحة مسبقاً (كل كلمة يقابلها عدد صحيح) وبالتالي قمت أولاً بحشوها لكي تكون جميعها بنفس الحجم (خطوة إجبارية) لكنك لم تحدد الطول الأعظمي لل padseq وبالتالي سيختار افتراضياً طول أطول مستند (في حالتك فإن أطول مستند طوله 2494) أي كل عينات بياناتك سيكون حجمها 2494 (بعد الحشو بأصفار) وبالتالي يكون حجم الإدخال لديك هو (عدد العينات,عدد الفيتشرز) وعدد الفيتشرز هنا أو "السمات" features هو طول التسلسلات أي 2494. لذا يجب أن تقوم بتحديده لشبكتك. طبعاً عدد العينات لامشكلة في عدم تحديده فأيضاً يستطيع كيراس استنتاجه. وبالتالي يكون حل مشكلتك إما باستخدام الوسيط input_length كونك تتعامل مع طبقة NLP أو من خلال input_shape كالتالي: from keras.datasets import imdb from keras import preprocessing max_features = 1000 # حدد حجم الإدخال الذي تريده maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) # حدد طول التسلسل الذي تريده x_train = preprocessing.sequence.pad_sequences(x_train,maxlen=maxlen) x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) from keras.models import Sequential from keras.layers import Flatten, Dense,Embedding model = Sequential() # قم الآن بتعريف حجم طبقة الإدخال لشبكتك model.add(Embedding(1000, 8, input_shape=(maxlen,))) # أو # model.add(Embedding(1000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='tanh')) model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc']) history = model.fit(x_train, y_train, epochs=3, batch_size=64, validation_split=0.2) ,طبعاً يفضل أن تمرر لتابع ال padseq طول التسلسل (الطول الأعظمي الذي تريده) لكي لايقوم باستخدام الطول الأكبر، فهذا قد يسبب لك مشاكل في التدريب (بطء شديد لاتخاذك طول كبير جداً)

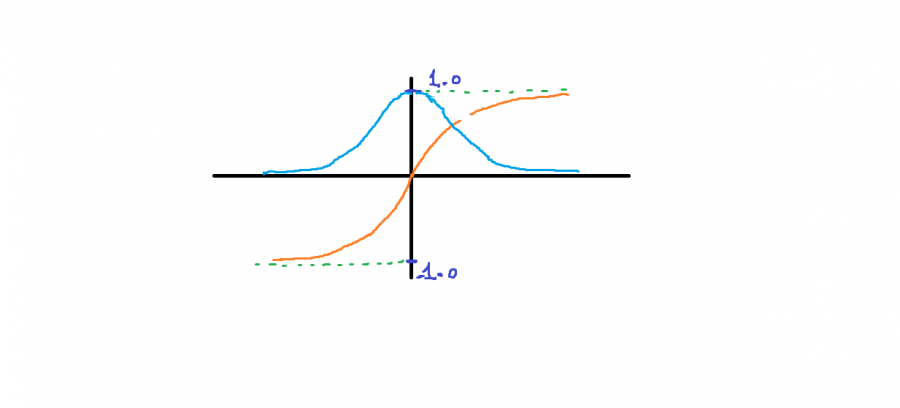
دالة غير خطية، تشبه كثيراً التابع السيني Sigmoid ولكن الفرق بينهما في مجال قيم الخرج حيث يكون في ال tanh من 1- إلى 1، أي على عكس التابع السيني حيث يكون الخرج من 0 إلى 1. ولها الشكل التالي (الاورنج): من الشكل نلاحظ أنها تأخذ أي قيمة حقيقية كقيم مدخلات. والخرج يكون في النطاق من 1 إلى -1. كلما كانت المدخلات أكبر (أكثر إيجابية) ، كلما كانت قيمة المخرجات أقرب إلى 1.0 ، بينما كلما كانت المدخلات أصغر (أكثر سلبية) ، كلما كان الناتج أقرب إلى -1.0. ومن الرسم البياني نلاحظ أيضاً أنه يمكن استخدامها في تدريب النماذج (مستمر و قابل للإشتقاق في كل مكان)، وكما نلاحظ من الرسم (المنحني الأزرق) فإن المشتق تكون قيمه فعالة للتدريب عندما تكون قيم z قريبة من الصفر (حولها) ولكن من أجل قيم كبيرة جداً أو صغيرة جداً فلن تكون فعالة في التدريب لأن المماس يكون شبه مستقيم وبالتالي قيمة المشتقة تكون صغيرة جداً، مما يؤدي الى بطء شديد في عملية التدريب وبالتالي مكلف من الناحية الحسابية. إن الميزة الأهم في هذا التابع مقارنة بال sigmoid هو أن قيم المشتقات أكبر وبالتالي تدرجاته (Gredint) تكون أكثر قوة نحو القيم الصغرى الشاملة GM أي بمعنى آخر أسرع في التقارب Converge وهذا مايجعله أكثر كفاءة مقارنة بالتابع السيني. أما عيبها فكما ذكرنا هو نفس المشكلة التي تعاني منها sigmoid وهي مشكلة تلاشي التدرجات "vanishing gradient" (المشتقات يصغر حجمها إلى أن تنعدم تقريباً عندما تزداد قيمة Z وهذا واضح من المنحني الأزرق). عند استخدام tanh للطبقات المخفية ، أنصح باستخدام تهيئة الوزن "Xavier Normal" أو "Xavier Uniform" (يُشار إليها أيضاً بتهيئة Glorot) إضافة إلى تقييس "scaling" بيانات الدخل إلى النطاق -1 إلى 1 قبل التدريب. وفي كيراس له الشكل التالي: tf.keras.activations.tanh(x) ويمكنك استخدامه في الطبقات الخفية لنموذجك (لاتستخدمه مع طبقة الخرج فكيراس لاتعالج حالته، رغم أنه يمكن استخدامه)، انظر للمثال التالي: from keras.datasets import imdb from keras import preprocessing max_features = 10000 maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) x_train = preprocessing.sequence.pad_sequences(x_train, maxlen=maxlen) # هنا حددنا طول الكلمات ب 20 x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) # بناء نموذجك from keras.models import Sequential from keras.layers import Flatten, Dense model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='tanh'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.tanh)) أو بالشكل التالي model.add(Dense(64)) model.add(Activation(activations.tanh)) """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary() # تدريبه history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2)

تعديل:لم انتبه لكامل سؤالك: الآن بالنسبة لما تريده فلا يوجد حل مباشر (تابع معرف في نمباي) وإنما يجب أن تقوم بحيلةً ما، لذا فهناك حلان، الحل الأول، أن تقوم بتعريف مصفوفة وتقوم بتهيئتها، ثم استبدال كل القيم فيها عمود عمود، أو الأسطر: import numpy arr = numpy.zeros(shape=(3,2)) arr """ array([[0., 0.], [0., 0.], [0., 0.]]) """ # إضافة عمود arr[:,0]=[3,1,2] arr """ array([[3., 0.], [1., 0.], [2., 0.]]) """ arr[:,1]=[4,1,2] arr """ array([[3., 4.], [1., 1.], [2., 2.]]) """ وهو حل قد يكون مربك قليلاً ولايحقق ماطلبته (أنت تريد البدء من مصفوفة فارغة تماماً أي [] كما في القوائم)، لذا الآن إليك خدعتي الخاصة، التي تمكنك من التلاعب كيفما شئت. سأعطيك مثال عليها ، أولاً لإضافة عناصر للمصفوفة عمود عمود بدءاً من مصفوفة فارغة أي []: # تعريف مصفوفة ثنائية فارغة ب 3 أسطر X = np.array([[],[],[]]) X.shape #(3, 0) X=np.append(X, [[1],[2],[4]], axis = 1) X.shape # (3, 1) X """ array([[1.], [2.], [4.]]) """ X=np.append(X, [[3],[5],[6]], axis = 1) X.shape # (3, 2) """ array([[1., 3.], [2., 5.], [4., 6.]]) """ حيث يجب عليك تحديد عدد الأسطر فقط، في المصفوفة. وإذا وجدت أن إضافة الأسطر يدوياً أمر متعب يمكنك القيام بما يلي: #سطر n إضافة X = np.array([[]]) # مثلاً تريد أن تكون عدد أسطرك 100 for i in range(99): X=np.append(X, [[]], axis = 0) X.shape # (100, 0) """ الآن يمكنك إضافة ماتريده من أعمدة أو أسطر اعتماداً على هذا الأسلوب """ أما إذا أردت الإضافة سطر سطر، فقم بالتغيير البسيط التالي: #عمود n إضافة # أو بمعنى آخر عدد الأعمدة X = np.array([[]]) # فقط نقوم بتعريف مصفوفة فارغة كما أردت # مثلاً تريد أن يكون عدد أعمدتك 100 for i in range(99): X=np.append(X, [[]], axis = 0) (X.reshape(0,100)).shape # (0, 100) """ الآن يمكنك إضافة ماتريده من أسطر اعتماداً على هذا الأسلوب """ مثال: X = np.array([[],[]]).reshape(0,2) X=np.append(X, [[1,5]], axis = 0) X #array([[1., 5.]]) X.shape # (1, 2)

لإضافة عمود إلى مصفوفتك استدعي numpy.append(arr, values, axis=1) ، انظر للمثال التالي: import numpy as np arr = np.zeros((3,2)) print(arr) """ [[0. 0.] [0. 0.] [0. 0.]] """ new_column = [[3],[3], [6]] arr = np.append(arr, new_column, axis=1) arr """ array([[0., 0., 3.], [0., 0., 3.], [0., 0., 6.]]) """ ولإضافة أسطر، فقط نغير المحور: import numpy as np arr = np.zeros((3,2)) print(arr) """ [[0. 0.] [0. 0.] [0. 0.]] """ new_row = [[3,2]] arr = np.append(arr, new_row, axis=0) arr """ array([[0., 0.], [0., 0.], [0., 0.], [3., 2.]]) """ أو يمكنك استخدام numpy.insert(arr, idx, values, axis=1): import numpy as np arr = np.zeros((3,2)) print(arr) """ [[0. 0.] [0. 0.] [0. 0.]] """ new_column = [[3,2,1]] arr=np.insert(arr, 1, new_column, axis=1) print(arr) """ [[0. 3. 0.] [0. 2. 0.] [0. 1. 0.]] """

يمكن لكل من array و asarray تحويل البيانات المهيكلة "structured data" إلى ndarray ، ولكن الاختلاف الرئيسي هو أنه عندما يكون مصدر البيانات ndarray ، ستظل المصفوفة تنسخ نسخة ، وتحتل ذاكرة جديدة ، لكن asarray لن تفعل ذلك. عند الإدخال كقائمة ، يكون نوع البيانات الأصلي الذي يتم تحويله عبارة عن قائمة: import numpy x=[[0,5],[8,5]] v = numpy.asarray(x) i = numpy.array(x) x[0] = 5 print(x) #[5, [8, 5]] print(i) ''' [[0 5] [8 5]] ''' print(v) ''' [[0 5] [8 5]] ''' من هذا يمكننا أن نرى أن ال array هو نفسه asarray ، أي يقومان بتحويل المدخلات إلى تنسيق Matrix. وعندما يكون الدخل عبارة عن قائمة، فإن تغيير قيمة في القائمة لا يؤثر على القيمة المحولة إلى المصفوفة. أما عندما يكون الإدخال عبارة عن مصفوفة: import numpy as np array=np.random.random((3,3)) print(array.dtype) # float64 x=np.array(array,dtype='float64') t=np.asarray(array,dtype='float64') array[1]=2 print(array) ''' [[0.14427798 0.24129013 0.3114457 ] [2. 2. 2. ] [0.18134186 0.29733322 0.38294914]] ''' print(x) ''' [[0.14427798 0.24129013 0.3114457 ] [0.21828251 0.48710077 0.07849822] [0.18134186 0.29733322 0.38294914]] ''' print(t) ''' [[0.14427798 0.24129013 0.3114457 ] [2. 2. 2. ] [0.18134186 0.29733322 0.38294914]] ''' print(x is a) # False print(t is a) # True من النتائج المذكورة أعلاه يمكننا أن نرى الفرق بين np.array و np.asarray. عندما يكون الإدخال عبارة عن مصفوفة ، ستقوم np.array بإنشاء مساحة ذاكرية وتنسخ البيانات فيها. أي سيكون لها مساحة ذاكرة خاصة بها، لذلك يتغير الخرج الخاص ب np.array مع الدخل، والتابع .asarray يزيد من العداد الذي يشير إلى t ويشير إلى المصفوفة، بحيث عندما تتغير المصفوفة الأصلية ، سيتغير ناتج np.asarray أيضًا.

تكون Numpy matrices ثنائية الأبعاد حصراً، بينما تكون المصفوفات المعقدة (ndarrays) أي ذات N أبعاد. وكائنات Matrix هي صف فرعي من ndarray ، لذلك فهي ترث جميع ال attributes والتوابع من ndarrays. إن الميزة الرئيسية ل Numpy matrices أنها توفر طريقة مريحة لضرب المصفوفات، أما بالنسبة لمصفوفات نمباي فإنه بدءاً من Python 3.5 أصبحت نمباي تدعم ضرب المصفوفات بطريقة مريحة عن طريق استخدام المعامل "@"، انظر: import numpy as np x = np.mat('2 2; 0 3') print(x) """ [[2 2] [0 3]] """ y = np.mat('4 1; 4 2') print(y) """ [[4 1] [4 2]] """ print(x*y) """ [[16 6] [12 6]] """ #ndarray استخدام نمباي import numpy as np x = np.array([[2,2], [0 ,3]]) print(x) """ [[2 2] [0 3]] """ y = np.array([[4, 1], [4, 2]]) print(y) """ [[4 1] [4 2]] """ print(x@y) # print(np.dot(x,y)) أو """ [[16 6] [12 6]] """ أيضاً كلاهما يدعمان العامل .T لحساب منقول المصفوفة "transpose" لكن كائنات mat لديها ميزات إضافية مثل حساب معكوس مصفوفة وال Conjugate transpose, x = np.array([[2,2], [0 ,3]]) a = np.mat('4 3; 2 1') print(x.T) print(a.T) print(a.H) #mat خاصة ب # Conjugate transpose print(a.I) #mat خاصة ب # inverse """ [[2 0] [2 3]] [[4 2] [3 1]] [[4 2] [3 1]] [[-0.5 1.5] [ 1. -2. ]] """ ومن ناحية استخدام العامل ** : # nd a = np.array([[4, 3], [2, 1]]) c = np.array([[4, 3], [2, 1]]) print(a@b) """[[13 20] [ 5 8]]""" print(a**2) """[[16 9] [ 4 1]]""" print(c**2) """ [[16 9] [ 4 1]] """ #matrix a = np.mat('4 3; 2 1') a**a """ [[16 9] [ 4 1]] """ هناك توابع أخرى مثل np.ravel لكنها غير مهمة. الميزة الرئيسية للمصفوفات matrix هي أنها أكثر عمومية من المصفوفات ثنائية الأبعاد. لكن عليك استخدام ndarray في حالة كانت البيانات ثلاثية الأبعاد أو أكثر، وليس كائن matrix.وطبعاً قد يكون المزج بينهما خلال بناء الكود فكرة سيئة أو متعبة لأنه يجب عليك ملاحقة المتغيرات والتدقيق منهم لكي لايعيد لك ناتج الضرب نتيجة غير متوقعة. وبشكل عام يمكنك الاعتماد كلياً على ndarray لكنك ستفقد بعض التوابع أو ال notation الموجودة في mat وغير الموجودة في nd. وأخيراً يمكنك التحويل بينهما من خلال np.asarray و np.asmatrix: # ndarrays a = np.array([[4, 3], [2, 1]]) np.asmatrix (a) """ matrix([[4, 3], [2, 1]]) """

انظر ببساطة: array = np.random.random(11) print(array) """ [0.68454984 0.29564049 0.43585867 0.08240091 0.64254513 0.6644243 0.19431044 0.8343987 0.80227567 0.3568269 0.73074224] """ # أما array = np.random.random(11) array """ array([0.68454984, 0.29564049, 0.43585867, 0.08240091, 0.64254513, 0.6644243 , 0.19431044, 0.8343987 , 0.80227567, 0.3568269 , 0.73074224]) """ أي عندما نستخدم التعليمة print سيظهر الخرج كما تريده، أما يالنسبة للتحكم بدقة الإخراج لل floatting point فيمكنك استخدام set_printoptions واستخدام الوسيطة precision وتحديد العدد الذي تريد إظهاره: import numpy as np array = np.random.random(11) print(array) """ [0.44945536 0.56544673 0.82679165 0.41418793 0.465158 0.34722955 0.75272122 0.01321709 0.24561376 0.86812281 0.761384 ] """ np.set_printoptions(precision=3) print(array) """ [0.449 0.565 0.827 0.414 0.465 0.347 0.753 0.013 0.246 0.868 0.761] """

يمكنك استخدام التابع التالي، حيث نعتمد على فكرة طرح القيمة المطلوبة من كل عنصر في المصفوفة، وبالتالي تتشكل لدينا مصفوفة الفرق بالقيمة المطلقة، ثم نستخدم التابع argmin ليعطينا موقع أصغر عنصر، ثم نستخدم flat لتعطينا القيمة الموافقة للموقع: import numpy as np array = np.random.random(10) print(array) """ [0.59588654 0.43663869 0.49730145 0.65410536 0.98261646 0.06100155 0.28296143 0.94809249 0.43775789 0.2167913 ] """ def find1(a, a0): index = np.abs(a - a0) print(idx) """ [0.10411346 0.26336131 0.20269855 0.04589464 0.28261646 0.63899845 0.41703857 0.24809249 0.26224211 0.4832087 ] """ index=idx.argmin() print(index) # 3 print(a.flat[index]) # 0.6541053630832852 return a.flat[index] find1(array,0.7) # 0.6541053630832852 الآن سأكتب التابع بشكل مختصر: import numpy as np array = np.random.random(10) def find1(a, a0): index = np.abs(a - a0).argmin() return a.flat[index] find1(array,0.7) أو يمكنك استخدام الطريقة التالية وهي مشابهة إلى حد كبير بالطريقة الأولى (بالشكل والسرعة): import numpy as np #array = np.random.random(10) print(array) """ [0.59588654 0.43663869 0.49730145 0.65410536 0.98261646 0.06100155 0.28296143 0.94809249 0.43775789 0.2167913 ] """ def find2(a, values): index = np.abs(np.subtract.outer(array, values)).argmin(0) return a.flat[index] find2(array,0.7) # 0.6541053630832852 أو بالطريقة التالية حيث نعتمد على ترتيب المصفوفة أولاً وهي عموماً لاتحتاج لاستخدام نمباي معها، وهي تأخذ المصفوفة المراد البحث فيها والقيمة التي نبحث عن أقرب قيمة لها وترد لنا الموقع الموجودة فيه، ويتم إرجاع -1 أو طول المصفوفة للإشارة إلى أن القيمة خارج النطاق أدناه وأعلى بالترتيب: import numpy as np array = np.random.random(10) print(array) def bi(a,val): a=np.sort(a) """ [0.06100155 0.2167913 0.28296143 0.43663869 0.43775789 0.49730145 0.59588654 0.65410536 0.94809249 0.98261646] """ n = len(a) if (val < a[0]): return -1 elif (val > a[n-1]): return n jl = 0 # تهيئة أقل حد ju = n-1 # الأعلى # طالما لم يتحقق الشرط التالي # نكرر حتى يتحقق الشرط while (ju-jl > 1): jm=(ju+jl) >> 1 # احسب القيمة في المنتصف مع إزاحة if (val >= array[jm]): jl=jm # واستبدل إما الحد الأدنى else: ju=jm # أو الأعلى if (val == a[0]): return 0 elif (val == a[n-1]): return n-1 else: return jl bisection(array,0.7) # 0.6541053630832852 الآن سأجري مقارنة بينهم: import numpy as np def bi(array,value): array=np.sort(array) n = len(array) if (value < array[0]): return -1 elif (value > array[n-1]): return n jl = 0 ju = n-1 while (ju-jl > 1): jm=(ju+jl) >> 1 if (value >= array[jm]): jl=jm else: ju=jm if (value == array[0]): return 0 elif (value == array[n-1]): return n-1 else: return jl def find1(a, a0): index = np.abs(a - a0).argmin() return index def find2(a, values): index = np.abs(np.subtract.outer(array, values)).argmin(0) return index # المقارنة array = np.random.random(1000) %timeit bi(array,0.7) print(bisection(array,0.7)) %timeit find1(array,0.7) print(find1(array,0.7)) %timeit find2(array,0.7) print(find2(array,0.7)) """ 535 ns ± 19.5 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) -1 5.92 µs ± 1.02 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each) 537 6.37 µs ± 336 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) 537 """

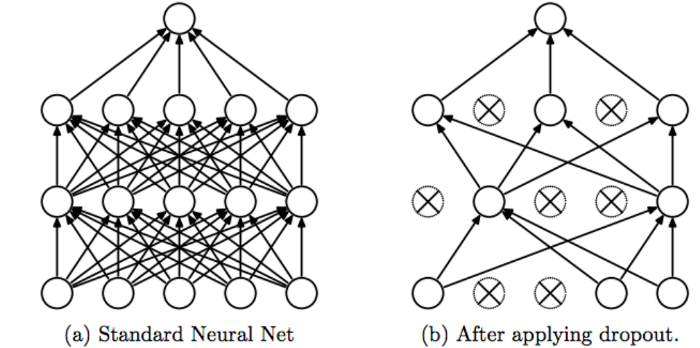
ال dropout أو "التسرب " هو إحدى تقنيات محاربة ال Overfitting (الضبط الزائد). مبدأ هذه التقنية هو تجاهل أو تعطيل بعض الخلايا (العصبونات) بشكل عشوائي في طبقات (أو طبقة) الشبكة العصبية. . تأمل الصورة التالية: وبالتالي سنقوم بمنع المودل من التركيز على خاصية "feature" معينة و نجبره على التعلم من كل الخصائص الموجودة لا أن يأخذ خاصية واحدة كقاعدة في التعلم ويعتمد عليها بشكل دائم. وبهذه الطريقة نتجنب حالة الـ overfitting ونتعلم من كل الخصائص الموجودة. أي أن الفكرة خلف هذه التقنية هي أنه في كل تكرار نقوم بتعطيل خلايا (نجعلها لاتشترك في التدريب والتوقع) بينما الخلايا المتبقية تشارك في عملية التدريب والتوقع، أي يستخدم مجموعة جزئية من العصبونات في كل تكرار (التكرار الواحد هو عملية انتشار أمامي (للتوقع) ثم انتشار خلفي(لتحديث قيم الأوزان)). أي أن تأثير هذه التقنية هو أن الشبكة تصبح أقل حساسية للأوزان المحددة للخلايا العصبية. ينتج عن هذا بدوره شبكة قادرة على التعميم "generalization " بشكل أفضل ومن غير المرجح أن تقع في ال OF على بيانات التدريب. ويمكننا أن نقول أيضاً أن الشبكة لن تقوم بحفظ مسار أو سلوك معين في عملية التوقع. انظر للصورة التالية: وفي كيراس يمكنك استخدامها بالشكل التالي: from tensorflow.keras.layers import Dropout Dropout(rate) حيث أن ال rate هو معدل الحذف ويأخذ قيمة بين 0 و 1. فمثلاً عند وضع 0.5 أي سيتم تعطيل 50% من العصبونات، وتعتبر هذه القيمة من الـ hyper parameters أيضاً التي يجب ضبطها في نموذجك بشكل دقيق. فاختيار قيم كبيرة لل rate (فوق 0.5) قد يؤدي إلى مشكلة جديدة وهي ال Underfitting. يجب أن تعلم أيضاً أنه يتم استخدام التسرب فقط أثناء تدريب النموذج ولا يتم استخدامه عند التقييم النهائي للنموذج (مرحلة التدريب مثلاً أو الاستخدام العملي) أي بمعنى آخر يستخدم فقط في مرحلة التدريب أما في مرحلة الاختبار أو الاستخدام فإنه تلقائياً لايتم إشراكها في عملية التوقع. الآن سأعطيك مثال عملي عليه أثناء بناء نموذج لتصنيف الأرقام المكتوبة بخط اليد: from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, Conv2D, Dropout, Flatten, MaxPooling2D # تحميل البيانات import tensorflow as tf (x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() x_train.shape # (60000, 28, 28) # 4-dims تحويل المصفوفة إلى شكل رباعي الأبعاد x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) x_test = x_test.reshape(x_test.shape[0], 28, 28, 1) input_shape = (28, 28, 1) # لنتمكن من الحصول على الفواصل العشرية بعد القسمة x_train = x_train.astype('float32') x_test = x_test.astype('float32') # Normalizing x_train /= 255 x_test /= 255 print('x_train shape:', x_train.shape) print('Number of images in x_train', x_train.shape[0]) print('Number of images in x_test', x_test.shape[0]) # بناء النموذج model = Sequential() model.add(Conv2D(32, kernel_size=(3,3), input_shape=input_shape)) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Flatten()) model.add(Dense(128, activation=tf.nn.relu)) model.add(Dropout(0.2)) # هنا أضفنا طبقة model.add(Dense(10,activation=tf.nn.softmax)) # تجميع النموذج model.compile(optimizer='rmsprop', loss='sparse_categorical_crossentropy', metrics=['acc']) model.fit(x_train,y_train, epochs=9) model.evaluate(x_test, y_test) # 98.5% حيث نضيفها بعد الطبقة التي نريد تطبيق التسرب عليها، وهنا قمنا بإضاففتها بعد الطبقة dense(128) أي أن هذه الطبقة سيتم تطبيق التسرب عليها خلال عملية التدريب وبالتالي في كل كل تكرار سيتم تعطيل (أو تجاهل) 20% من الخلايا فيها بشكل عشوائي، أي في كل تكرار ستشترك 102 خلية في التدريب والتوقع وسيتم تجاهل باقي الخلايا. وطبعاً يمكنك إضافتها بعد كل طبقة من طبقات نموذجك (هذا يرجع لك حسب تقديرك للمشكلة وماتتطلبه). لكن لاتستخدمها في بداية النموذج أي بعد التعليمة sequential لأنه في هذه الحالة تكون قد طبقتها على طبقة الدخل وبالتالي سيتم تجاهل قسم من ال features الخاصة بعيناتك وهذا أمر غير محبذ أبداً.

عادة ماينتج هذا الخطأ عندما يكون حجم البيانات قليل، وبالتالي ينشأ هذا الخطأ بسبب حجم ال batch_size الذي اخترته حيث لايجب أن يكون حجمه أقل من حجم بيانات التدريب لديك، حيث أنه في معظم الحالات ، يكون سبب هذا الخطأ هو أن حجم بيانات التدريب أقل من حجم الدُفعة، لذا تأكد أولاً من أن with_noise يحتوي على 140 عينة على الأقل أو قم بتقليل حجم الدفعة (batch_size ). أي مثلاً اجعل حجمه 64 أو 32 أو اجعله Batch GD أي 1. float validation_split = 2f; Sequential model = new Sequential(); no_noise = no_noise.astype(np.float32); with_noise = with_noise.astype(np.float32); no_noise /= 255; with_noise /= 255; # بناء النموذج model.Add(new Conv2D(128, kernel_size: new Tuple<int, int>(5, 5), activation: "tanh", input_shape: new Shape(45, 45,1))); model.Add(new Conv2D(64, kernel_size: new Tuple<int, int>(3, 3), activation: "tanh")); model.Add(new Conv2DTranspose(64, kernel_size : new Tuple<int,int> (3, 3), kernel_constraint : max_norm, activation: "tanh")); model.Add(new Conv2DTranspose(32, kernel_size : new Tuple<int,int> (3, 3), activation: "relu")); model.Add(new Conv2D(1, kernel_size : new Tuple<int,int>(3, 3), activation: "sigmoid", padding: "same")); model.Compile(optimizer: "rmsprop", loss: "binary_crossentropy"); model.Fit(with_noise, no_noise,epochs: 10,batch_size: 64,steps_per_epoch:2,validation_split: validation_split);

في القسم الثاني ينتج الخطأ، حيث يتم توقع كل خطوة في التسلسل (خطوة خطوة). وهذا يتطلب أن يكون حجم ال batch_size مساوي ل 1 أي: Online Learning (Batch Size = 1) أي الحل يتغيير حجم الباتش كالتالي: #sequence إنشاء تسلسل length = 10 s= [i/float(length) for i in range(length)] # إنشاء أزواج x/y df = DataFrame(s) df = concat([df, df.shift(1)], axis=1) df.dropna(inplace=True) val = df.values data = val[:, 0] label=val[:, 1] data = data.reshape(len(data), 1, 1) # القسم 0 n_batch = 1 # هنا n_epoch = 800 n_neurons = 12 model = Sequential() model.add(LSTM(n_neurons, batch_input_shape=(n_batch, data.shape[1], data.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mse', optimizer='rmsprop') # القسم 1 for i in range(n_epoch): model.fit(data, label, epochs=1, batch_size=n_batch, verbose=1, shuffle=False) model.reset_states() # القسم 2 for i in range(len(data)): testX, testy = data[i], label[i] testX = testX.reshape(1, 1, 1) yhat = model.predict(testX, batch_size=1) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat)) هذا يعني أنه سيتم تحديث أوزان الشبكة بعد كل عينة تدريبية. وطبعاً هذا سيعطيك سرعة أكبر لكن التدريب لن يكون مستقراً. طريقة أخرى، وهي تنفبذ كل التنبؤات دفعة واحدة، أي: Batch Forecasting (Batch Size = N) وبالتالي يكون التعديل: # القسم 2 yhat = model.predict(data, batch_size=n_batch) for i in range(len(label)): print('>Expected=%.1f, Predicted=%.1f' % (label[i], yhat[i])) لكن هذا يعني أننا قد نكون مقيدين للغاية في طريقة استخدام النموذج، سيتعين علينا استخدام جميع التنبؤات التي تم إجراؤها مرة واحدة ، أو الاحتفاظ بالتنبؤ الأول فقط وتجاهل الباقي. لذا فالحل الأفضل هو استخدام أحجام دفعات مختلفة للتدريب والتنبؤ. طريقة القيام بذلك هي نسخ الأوزان من الشبكة التي تم تدريبها وإنشاء شبكة جديدة باستخدام الأوزان المدربة مسبقاً. يمكننا القيام بذلك باستخدام وظائف get_weights () و set_weights () في Keras API ، على النحو التالي: # إعادة تعيين حجم الدفعة n_batch = 1 # إعادة تعريف النموذج new_model = Sequential() new_model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True)) new_model.add(Dense(1)) # copy weights عملية old_weights = model.get_weights() new_model.set_weights(old_weights) يؤدي هذا إلى إنشاء نموذج جديد يتم تجميعه compile بحجم دفعة 1. يمكننا بعد ذلك استخدام هذا النموذج الجديد لعمل تنبؤات من خطوة واحدة: # القسم 2 for i in range(len(data)): testX, testy = data[i], label[i] testX = testX.reshape(1, 1, 1) yhat = new_model.predict(testX, batch_size=n_batch) print('>Expected=%.1f, Predicted=%.1f' % (testy, yhat))

التطبيقات التي تنقل الصور عبر الانترنت أغلبها يقوم بعملية ضغط للصور، وواتساب هو أحد التطبيقات التي تقوم بذلك عند مشاركة المحتوى عليه، لذا تبدو الصور أقل دقة.

بالنسبة لمتصفح كروم، سيكون عليك تعليم متصفح Chrome الخاص بك كيفية معاينة ملفات PDF، لذا قم بتحميل الإضافة install a PDF preview إلى متصفحك، ثم: Automatically previews pdfs, powerpoint presentations, and other documents in Google Docs Viewer. أو يمكنك عادةً فتح ملفات PDF تلقائيًا في Chrome بالنقر فوق الملف الذي تريد رؤيته. إذا كان يتم تنزيل ملفات PDF الخاصة بك بدلاً من فتحها تلقائيًا في Chrome ، فقد يكون السبب أنه تم إيقاف تشغيل عارض PDF في Chrome. لذا، على جهاز الكمبيوتر الخاص بك ، افتح Chrome. في الجزء العلوي الأيسر ، انقر على "مزيد من الإعدادات". في الجزء السفلي ، انقر فوق إظهار الإعدادات المتقدمة. ضمن "الخصوصية" ، انقر فوق إعدادات المحتوى. ضمن "مستندات PDF" ، حدد المربع بجوار "فتح ملفات PDF في تطبيق عارض PDF الافتراضي". (قم بإلغاء تحديد هذا المربع إذا كنت تريد فتح ملفات PDF تلقائيًا عند النقر فوقها). وبالنسبة لفيرفوكس قم بتثبيت الإضافة pdf.js، أو يمكنك استخدام الطريقة التالية : https://docs.google.com/viewerng/viewer?url=http://yourfile.pdf #yourfile.pdf استيدلها بالرابط الذي تريده

التابع count تم تعريفه للاستخدام مع القوائم ولكنه غير معرف من أجل المصفوفات ولهذا السبب ظهر لديك هذا الخطأ، والحل كالتالي، نقوم بتحويل المصفوفة إلى قائمة عن طريق الباني list ثم نطبق عليها التابع: a = np.arange(10) a=np.array([0, 11, 11, 3, 4, 11, 6, 7, 8, 9]) serach=11 list(a).count(serach) # 3 لكن هذه الطريقة يمكنك استخدامها فقط في حالة كانت مصفوفتك أحادية الأبعاد. أما في حالة كانت مصفوفتك متعددة الأبعاد فيمكنك اسخدام خدعتي السحرية لحل المشكلة، وهي استخدام التابع reshape لتحويل المصفوفة من مصفوفة متعددة الأبعاد ثم استخدام التايع count معها: a = np.arange(10) a=np.array([[8, 9],[8, 8]]) a=a.reshape(-1) serach=8 list(a).count(serach) # 3 ويمكنك استخدام التابع np.bincount(a) أيضاً بنفس الطريقة (هذا التايع أيضاً يقوم بحساب التكرار للمصفوفات أحادية الأبعاد فقط، وبالتالي نستخدم نفس التكتيك السابق لحل المشكلة) حيث يعيد لك تكرارات كل العناصر: a = np.arange(10) a=np.array([[8, 9],[8, 8]]) a=a.reshape(-1) print(a) # [8 9 8 8] serach=8 np.bincount(a) # array([0, 0, 0, 0, 0, 0, 0, 0, 3, 1], dtype=int64) إن مايميز هذا التابع هو سرعته الغير قابلة للمقارنة ببقية الطرق. وأيضاً يمكنك استخدام التابع Counter ينفس الأسلوب، حيث تعيد قاموس بكل قيمة وتكراراتها: a = np.arange(10) a=np.array([[8, 9],[8, 8]]) a=a.reshape(-1) print(a) # [8 9 8 8] from collections import Counter Counter(a) # Counter({8: 3, 9: 1}) وأيضاً يمكنك استخدام التابع count_nonzero : a = np.arange(10) a=np.array([[8, 9],[8, 8]]) np.count_nonzero(a == 8) # 8 a = np.zeros((3,2,2)) np.count_nonzero(a == 0) # 12 أو من خلال np.sum : a = np.array([3,4,5,5,6]) np.sum(a == 5) # 2 أو من خلال التابع unique ثم zip: a = np.array([3,4,5,5,6]) unique, counts = np.unique(a, return_counts=True) dict(zip(unique, counts)) # {3: 1, 4: 1, 5: 2, 6: 1} مايلي هو مقارنة في السرعة بين التحقيقات السابقة: choices = np.random.randint(0, 100, 10000) %timeit [ np.sum(choices == k) for k in range(min(choices), max(choices)+1) ] %timeit np.unique(choices, return_counts=True) %timeit np.bincount(choices, minlength=np.size(choices)) # الأفضل %timeit [ np.count_nonzero(choices == k) for k in range(min(choices), max(choices)+1) ] %timeit [ list((choices.reshape(-1))).count(k) for k in range(min(choices), max(choices)+1) ] %timeit Counter(((choices.reshape(-1)))) """ 8.04 ms ± 801 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) 596 µs ± 88 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each) 44.5 µs ± 5.52 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each) 5.02 ms ± 429 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) 390 ms ± 21.4 ms per loop (mean ± std. dev. of 7 runs, 1 loop each) 2.66 ms ± 166 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) """

ترجع الدالة l.index(x) فهرس i بحيث i هو يمثل أول فهرس ظهرت فيه x في القائمة.. وبالتالي يمكننا أن نفترض وبشكل آمان أن دالة index () في Python يتم تنفيذها بحيث تتوقف بعد العثور على المطابقة الأولى، وهذا يؤدي إلى تحسين الأداء (تحسين زمن التنفيذ، حيث أنها تتوقف بعد عثورها على العنصر مباشرة بدل أن تكمل بدون فائدة).للعثور على عنصر يتوقف بعد التطابق الأول في مصفوفة NumPy ، استخدم المكرر ndenumerate: a = np.arange(10) a # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) next((idx for idx, val in np.ndenumerate(a) if val==3)) # 3 هناك وظائف أخرى في NumPy (argmax و where و nonzero) يمكن استخدامها للعثور على عنصر في مصفوفة، لكن جميعها لها عيب في المرور عبر المصفوفة بأكملها بحثاً عن جميع حالات التطابق، ولم يتم تحسينها للعثور على العنصر الأول فقط أي أول تطابق. لاحظ أيضاً أن where و nonzero يرجعان المصفوفات ، لذلك تحتاج إلى تحديد العنصر الأول للحصول على الفهرس. لاحظ المثال التالي: a = np.arange(10) a=np.array([0, 11, 2, 3, 4, 5, 6, 7, 8, 9]) np.argmax(a==11) # 1 np.where(a==11) # (array([1], dtype=int64),) np.nonzero(a==11) # (array([1], dtype=int64),) # وبالتالي يجب أن نكتب np.nonzero(a == 11)[0][0] # 1 np.where(a==11) [0][0]# 1 لذا فهذه الطريقة تعتبر أسرع خصوصاً عندما يكون العنصر الذي تبحث عنه موجوداً في بداية المصفوفة.

لفرز عناصر مصفوفة هناك عدة طرق للقيام بذلك، أولها استخدام التابع argsort من نمباي، حيث يعيد مؤشرات أو فهارس من المصفوفة، هذه المؤشرات يمكننا استخدامها لترتيب مصفوفتنا، سأعطيك الآن مثال لكيفية الاستفادة من هذا. لتكن لدينا المصفوفة التالية: import numpy as np a = np.random.randint(70, size=(3, 3)) a """ array([[ 0, 33, 32], [53, 44, 4], [36, 34, 0]]) """ سنقوم أولاً باستعداء التابع argsort على العمود الأول من المصفوفة، وبالتالي ستحصل على هذه النتيجة: a[:, 0].argsort() # array([0, 2, 1], dtype=int64) يوضح الخرج أن أصغر قيمة في العمود الأول هي في الموضع 0 (رقم السطر الموجودة فيه). وهذا صحيح ، فأقل قيمة في العمود الأول للمصفوفة هي 0، أما ثاني قيمة من الخرج هي 2 وهذا يعني أن ثاني أصغر قيمة في العمود الأول موجودة في الموضع 2 أي القيمة الثالثة أي 36 وهذا صحيح. أما ثالث قيمة من الخرج فتشير إلى ثالث أصغر قيمة في العمود وهكذا..، لفرز المصفوفة ، نحتاج الآن إلى استخدام المؤشرات التي أعطانا إياها التابع argsort لإعادة ترتيب الصفوف في المصفوفة. ويمكننا القيام بذلك عبر إجراء بسيط يمكن القيام به في سطر واحد من التعليمات البرمجية. إذاً سنستخدم نتيجة argsort على أنها فهارس الصف وسنضع الناتجة في a (مصفوفتنا) ، على النحو التالي: a = a[a[:, 0].argsort()] a """ array([[ 0, 33, 32], [36, 34, 0], [53, 44, 4]]) """ كما ترى، تم ترتيب الصفوف الآن من الأقل إلى الأكبر وفقاً للعمود الأول. وللفرز في عمود مختلف، ما عليك سوى تغيير فهرس العمود. a = a[a[:, 1].argsort()] a """ array([[ 0, 33, 32], [53, 34, 0], [36, 44, 4]]) """ حسناً ماذا إذا أردت الفرز على أساس الأسطر؟! يمكن أيضاً فرز مصفوفة NumPy حسب قيم الصفوف. يتم تحقيق ذلك بنفس طريقة الفرز باستخدام الأعمدة. نحتاج فقط إلى تغيير مواضع الفهرسة. على سبيل المثال ، لنأخذ المصفوفة التالية، ثم نفرز الأعمدة حسب القيم في الصف الأول. للقيام بذلك ، ما عليك سوى تحريك الفهرس (0) إلى موضع الصف ونقل نتيجة الفرز التنظيمي إلى موضع العمود: import numpy as np a = np.random.randint(70, size=(3, 3)) a """ array([[44, 10, 23], [ 9, 32, 58], [67, 31, 39]]) """ a = a[:, a[0, :].argsort()] a """ array([[10, 23, 44], [32, 58, 9], [31, 39, 67]]) """ في بعض الأحيان يكون من الضروري الفرز على أكثر من عمود واحد. أحد الأمثلة على ذلك هو البيانات التي تحتوي على السنة والشهر واليوم والقيمة في أعمدة منفصلة. يمكن أن يتعامل ترتيب Argsort في NumPy مع فرز أعمدة متعددة باستخدام الوسيطة اللطيفة. لنبدأ بإنشاء مصفوفة من 4 أعمدة تمثل السنة والشهر واليوم والقيمة. arr = np.array([[2019, 2, 1, 40], [2021, 4, 1, 80], [2020, 3, 2, 22], [2018, 1, 3, 11], [2021, 3, 9, 79]]) """ array([[2018, 1, 3, 11], [2019, 2, 1, 40], [2020, 3, 2, 22], [2021, 3, 9, 79], [2021, 4, 1, 80]]) """ سنستخدم الآن argsort لفرز الأعمدة ، بدءاً من الأولوية الأقل. هذا يعني أننا إذا أردنا الفرز حسب السنة ، ثم الشهر ، ثم اليوم ، فنحن بحاجة إلى الفرز حسب اليوم أولاً ، ثم الشهر ، ثم العام. بالنسبة للكل ما عدا النوع الأول ، نحتاج إلى تحديد النوع على أنه "ترتيب مدمج" ، والذي سيحافظ على سياق الفرز السابق. وهذا موضح في التعليمات البرمجية التالية: # الفرز حسب اليوم arr = arr[arr[:, 2].argsort()] # حسب الششهر arr = arr[arr[:, 1].argsort(kind='mergesort')] # حسب السنة arr = arr[arr[:, 0].argsort(kind='mergesort')] يمكنك استخدام طرق أخرى أعقد أيضاً مثل استخدام lexsort من نمباي كما في المثال التالي: import numpy as np a = np.random.randint(70, size=(3, 3)) a """ array([[12, 11, 6], [25, 46, 64], [42, 41, 1]]) """ col=0 a[np.lexsort(([1,-1]*a[:,[1,col]]).T)] """ array([[42, 41, 1], [25, 46, 64], [12, 11, 6]]) """ أو يمكنك باستخدام الدالة sorted مع الوسيط لامدا، وتعيد قائمة (لذا قم بإعادة تحويل الخرج إلى نمباي): import numpy as np a = np.random.randint(70, size=(3, 3)) a """ array([[17, 46, 17], [39, 64, 54], [ 6, 19, 68]]) """ col=1 # العمود المراد الترتيب عليه a=sorted(a, key=lambda a_entry: a_entry[col]) np.array(a) """ [[ 6 19 68] [17 46 17] [39 64 54]] """ هذا كان كل ماقد يلزمك.

يمكنك القيام بذلك في نمباي حيث أنها تمكننا من إزالة الاقتطاع وعرض النتائج كما هي ويتم ذلك باستخدام numpy.set_printoptions() وذلك اعتماداً على الوسيط threshold الذي يأخذ القيمتين threshold = np.inf أو threshold = sys.maxsize أو عدد صحيح، من خلال هذا الوسيط يتم طباعة أول 1000 رقم بدون اقتطاع "بشكل افتراضي أي إذا لم نضع maxsize أو inf ": """ numpy.set_printoptions(precision=None, threshold=None, edgeitems=None, linewidth=None, suppress=None, nanstr=None, infstr=None, formatter=None) """ import numpy as np import sys nums = np.arange(100) np.set_printoptions(threshold=sys.maxsize) # هنا وضعنا أعلى عدد ممكن للعرض print(nums) """ [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99] """ #أو import numpy as np import sys nums = np.arange(100) np.set_printoptions(threshold=np.inf) print(nums) # انظر أيضاًَ import numpy as np import sys nums = np.arange(200) np.set_printoptions(threshold=1000,sign="-") print(nums) """ import numpy as np import sys nums = np.arange(200) np.set_printoptions(threshold=1000,sign="-") print(nums) [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199] """ أهم الوسطاء، precision عدد أرقام الدقة لطباعة النقطة العائمة floating point (الافتراضي 8). threshold العدد الإجمالي لعناصر المصفوفة التي تؤدي إلى التلخيص بدلاً من العرض الكامل للمصفوفة (الافتراضي 1000). لعرض المصفوفة كاملة بدون تلخيص، مرر sys.maxsize. أو np.inf. أما linewidth فهو عدد المحارف في كل سطر. ويمكنك أيضاً استخدام التابع tolist الذي يقوم بتحويلها إلى قائمة كالتالي: import numpy as np import sys nums = np.arange(200) print(nums.tolist()) """ [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199] """

هناك عدة طرق للقيام بذلك، أولها استخدام باندا: import pandas as pd import numpy as np # إنشاءمصفوفة a = np.arange(3,4).reshape(-1,2) # طباعة المصفوفة print(a) # تحويل المصفوفة إلى DataFrame df = pd.DataFrame(a) #CSV حفظ الداتافريم كملف df.to_csv("data1.csv", index=False) #يفضل إلغاء تخزين عمود الفهرس لأنه قد يسبب لك مشاكل عند إعادة تحميل الملف الطريقة الثانية هي استخدام numpy_array.tofile(): import numpy as np # إنشاء مصفوفة a = np.arange(3,4) # عرض المصفوفة print(a) #tofile() استخدام الطريقة #',' يجب أن تستخدم الفاصلة # إنشاء الملف a.tofile('data2.csv', sep = ',') استخدام numpy.savetext(): """ numpy.savetxt(fname, arr, fmt='%.18e', delimiter=' ', newline='\n', header='', footer='', comments='# ', encoding=None) """ import numpy as np # إنشاء مصفوفة arr = np.array([[11, 16, 3], [1, 0, 8]]) #CSV حفظ المصفوفة في ملف np.savetxt("a.csv", arr, delimiter = ",") لكن هنا سيتم تخزين البيانات في تنسيق أسي ك float مثل 2.000000000000000000e+00 لذا يجب عليك تغيير ال formatting باستخدام الوسيط fmt كما يلي: np.savetxt('a.csv', arr, fmt="%d", delimiter=",") طبعاً delimiter هو سلسلة أو حرف لاستخدامه كفاصل عنصر. و newline سلسلة أو حرف لاستخدامه كفاصل أسطر. و header تكتب سلسلة في بداية ملف txt أي ترويسة. أما footer فتكتب سلسلة في نهاية الملف (ذيل). و fmt افتراضياً تكون %.18e أي بالتنسيق الأسي. أما arr فهي مصفوفة أحادية أو ثنائية البعد حصراً. مثال آخر: import numpy as np arr = np.array([6, 1, 4, 2, 18, 9, 3, 4, 2, 8, 11]) np.savetxt('array.csv', [arr], delimiter=',', fmt='%d') # ستخزن بالشكل التالي # 6,1,4,2,18,9,3,4,2,8,11 مررنا المحدد "،" لجعله بتنسيق csv. تم قمنا بتمرير نوع التنسيق أيضاً كـ "٪ d" ، أي تخزين العناصر كأعداد صحيحة. وكما أشرت فإنه بشكل افتراضي، سيتم تخزين الأرقام بتنسيق عائم flotting point. وللتنويه أيضاً، إذا لم تقم بإحاطة مصفوفة numpy ب [] أي تحويلها إلى قائمة أثناء تمريرها إلى numpy.savetxt () فقد لا يعمل محدد الفاصلة، وسيستخدم "\ n" كمحدد افتراضي. لذا يفضل إحاطتها. مثال آخر مع إضافة ترويسة وذيل: np.savetxt('array_hf.csv', [arr], delimiter=',', fmt='%d' , header='A Sample 2D Numpy Array :: Header', footer='This is footer') """ # A Sample 2D Numpy Array :: Header 6,1,4,2,18,9,3,4,2,8,11 # This is footer """ مثال آخر مع مصفوفة ثنائية الأبعاد: arr2D = np.array([[11, 12, 13, 22], [21, 7, 23, 14], [31, 10, 33, 7]]) np.savetxt('2darray.csv', arr2D, delimiter=',', fmt='%d') """ 11,12,13,22 21,7,23,14 31,10,33,7 """ أيضاً، بدلاً من حفظ مصفوفة كاملة ثنائية الأبعاد في ملف csv ، إذا أردنا، يمكننا حفظ أعمدة أو صفوف فردية أو متعددة فقط. # حفظ عمود np.savetxt('a.csv', [arr2D[:,1]], delimiter=',', fmt='%d') """ 12,7,10 """ # حفظ سطر np.savetxt('aa.csv', [arr2D[1] ], delimiter=',', fmt='%d') """ 21,7,23,14 """ ولحفظ مصفوفة مهيكلة Structured Numpy array: dtype = [('Name', (np.str_, 10)), ('Marks', np.float64)] structure = np.array([('Ali', 21.2, 5), ('Eyad', 22.3, 4)], dtype=dtype) print(structure) # [('Ali', 21.2, 5) ('Eyad', 22.3, 4)] np.savetxt('structured.csv', structure, delimiter=',', fmt=['%s' , '%f', '%d'], header='Name,Marks,Age', comments='') """ Name,Marks,Age Ali,21.2, 5 Eyad,22.3, 4 """ وبما أن كل عنصر في المصفوفة الرقمية الخاصة بنا كان عبارة عن مزيج من سلسلة ، عدد عشري وعدد صحيح ، لذلك أثناء حفظه في ملف csv ، نقوم بتمرير خيارات التنسيق كلها أي ["٪ s" ، "٪ f" ، "٪ d"] ويمكنك لاحقاً تحميل الملف بعدة طرق، باستخدام loadtxt: from numpy import loadtxt # تحميل المصفوفة data = loadtxt('data.csv', delimiter=',') # طباعتها print(data) أو من باندا: import pandas as pd data = pd.read_csv("filename.csv") # عرض أول 5 أسطر من الملف data.head() # إذا أردت عرض أسطر أكثر مرر عددها إلى الوسيط التالي data.head(n=10)

عندما تكون عدد الأصناف n في مشكلتنا أكبر من 2، يجب أن تحوي طبقتك الأخيرة على n خلية بغض النظر عن نوع دالة التكلفة التي استخدمتها (أي حتى لو استخدمت sparse_categorical_crossentropy) حيث أن الغاية الأساسية من ال sparse_categorical_crossentropy هو الراحة في الاستخدام (عدم الاضطرار إلى تحويل البيانات إلى ترميز ال One-Hot)، لكنها لاتغنيك عن وجود عدد من الخلايا يطابق عدد الأصناف في آخر طبقة، وبما أنك تتعامل مع مهمة لتصنيف الأخبار ولديك 46 صنف وبالتالي يكون التصحيح: from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=10000) word_index = reuters.get_word_index() reverse_word_index = dict([(value, key) for (key, value) in word_index.items()]) decoded_newswire = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]]) import numpy as np def vectorize_sequences(sequences, dimension=10000): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) from keras.utils.np_utils import to_categorical one_hot_train_labels = to_categorical(train_labels) one_hot_test_labels = to_categorical(test_labels) from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(64, activation='relu', input_shape=(10000,))) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(46, activation='softmax')) # يجب أن يتطابق عدد الأصناف مع عدد المخرجات model.compile(optimizer='rmsprop', loss='sparse_categorical_crossentropy', metrics=['accuracy']) x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = train_labels[:1000] partial_y_train = train_labels[1000:] history = model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val)) للتنويه: هناك هدف آخر من استخدام sparse_categorical_crossentropy وهو زيادة الكفاءة في التخزين والأداء (فهي لاتحتاج إلى تمثيل الفئات في متجهات عالية الأبعاد إضافة إلى أنها تقلل عدد العمليات الحسابية اللازمة).

تستخدم بشكل أساسي مع الشبكات العصبية التلاففية CNN حيث غالباً ماتتبع طبقة ال CNN طبقة MaxPooling. مبدأياً تأمل الصورة التالية: هنا لدينا مصفوفة 4*4 ونافذة حجمها 2*2 تمر على المصفوفة (لاحظ أن النافذة التي حجمها2*2 تتحرك بمقدار خطوتين) في البداية كانت النافذة موضوعة على المربع الأحمر وبالتالي ستأخذ أكبر قيمة فيه هي 20، ثم ستمشي على المصفوفة أفقياً بمقدار خطوتين (أي بكسلين أفقياً) وبالتالي ستصيح النافذة موجودة على المربع الأصفر وبالتالي ستأخذ أكبر قيمة فيه وهي 30 ، الآن وصلنا لنهاية حدود المصفوفة وبالتالي ننزل بمقدار خطوتين (أي بكسلين عمودياً) وبالتالي تصبح النافذة على المربع الأزرق وأكبر قيمة هي 112 وهكذا.. لاحظ كيف تم اختزال أبعاد المصفوفة من 4*4 إلى 2*2. حسناً لماذا نستخدم هذه الطبقة؟ السبب الأول هو أنها تقوم بتخفيف العبء الحسابي "Reducing computational load" فنظراً لأن MaxPooling يقلل من دقة الإخراج المعطى من الطبقة التلافيفية، وبالتالي ستنظر الشبكة في مناطق أكبر من الصورة في وقت واحد ، مما يقلل من كمية المعلمات في الشبكة وبالتالي يقلل من الحمل الحسابي. والسبب الثاني هو "Reducing overfitting" فهي تساعد في محاربة الضبط الزائد، حيث أن الفكرة وراء عمل max pooling هو أنها بالنسبة لصورة معينة، ستبحث شبكتنا لاستخراج بعض الميزات الخاصة. فهي تبحث عن الحواف والمنحنيات والدوائر وما إلى ذلك من السمات التي تميز الصورة (يمكننا التفكير في وحدات البكسل الأعلى قيمة على أنها الأكثر نشاطاً). وبالتلي فهي تركز على البكسلات الأعلى قيمة وتتجاهل البكسلات الأقل قيمة. طبعاُ يمكننا أن نغير حجم النافذة وأن نغير حجم الخطوات أو أن نقوم بخطوة نسميها الحشو padding التي تقوم بحشو حدود المصفوفة بأصفار لكي تحافظ على أبعاد المصفوفة (الصورة). كيراس أو تنسرفلو تؤمن لك طريقة سهلة للقيام بهذا. لها الشكل التالي: tf.keras.layers.MaxPooling2D( pool_size=(2, 2), strides=None, padding="valid", data_format=None ) # الوسيط الأخير سأتحدث عنه في النهاية pool_size: يمثل حجم النافذة، ويمكنك إسناد عدد صحيح أو tuple بحيث إذا استخدمت عدد صحيح مثلاً 2 فهذا يعني أنك سوف تستخدم نافذة بحجم 2*2 وإما إذا استخدمت tuple فمثلاً (2,2) فهذا يعني أن حجم النافذة سيكون 2*2. الوسيط الثاني strides هو حجم الخطوة أي مقدار إزاحة النافذة، فمثلاً إذا اخترت (1,1) هذا يعني أنه ستتم إزاحة النافذة بمقدار 1 بكسل في العرض و 1 بكسل في الطول (النافذة تمشي على طول سطر المصفوفة بمقدار بكسل واحد وعندما تصل لنهاية أول سطر ستنزل للسطر التالي بمقدار بكسل واحد). أما بالنسبة لآخر وسيط فهو يمثل ال padding أي الحشو ففي حال استخدمت vaild فلن يتم حشو حدود المصفوفة بأصفار (أي لن يتم الحفاظ على أبعاد المصفوفة أي كما في المثال في الأعلى ويجب أن تعلم أن عملية الحشو هذه تتم بما يتلائم مع المصفوفة ولاتقلق فكيراس تتكفل بكل هذا الأمر) والمصفوفة الناتجة في هذه الحالة: output_shape = math.floor((input_shape - pool_size) / strides) + 1 (when input_shape >= pool_size) أما في حالة استخدمت same فسوف يقوم بعملية الحشو. والمصفوفة الناتجة في هذه الحالة: output_shape = math.floor((input_shape - 1) / strides) + 1 الآن انظر للأمثلة التالية: # مصفوفة بحجم 3*3 # حجم الخطوة هنا اخترناه بمقدار بكسل واحد # حجم النافذة اخترناها 2*2 #valid الحشو x = tf.constant([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) # قمت بتحويل مصفوفة ال 3*3 إلى مصفوفة ب 4 أبعاد لأن هذه الطبقة لاتستقبل إلى مصفوفة بأربع أبعاد كما سأوضح بعد قليل x = tf.reshape(x, [1, 3, 3, 1]) max_pool_2d = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(1, 1), padding='valid') c=max_pool_2d(x) # هنا قمت بتحويل الخرج من رباعي إلى ثنائي الأبعاد لتسهل قراءة الخرج tf.reshape(c, [ 2, 2]) # الخرج """ <tf.Tensor: shape=(2, 2), dtype=float32, numpy= array([[5., 6.], [8., 9.]], dtype=float32)> """ مثال آخر: # مصفوفة بحجم 3*3 # حجم الخطوة هنا اخترناه بمقدار بكسل واحد # حجم النافذة اخترناها 2*2 #same الحشو x = tf.constant([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) x = tf.reshape(x, [1, 3, 3, 1]) max_pool_2d = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(1, 1), padding='same') # تمت إضافةعمود بأصفار وسطر بأصفار للحفاظ على الأبعاد c=max_pool_2d(x) c tf.reshape(c, [ 3, 3]) """ <tf.Tensor: shape=(3, 3), dtype=float32, numpy= array([[5., 6., 6.], [8., 9., 9.], [8., 9., 9.]], dtype=float32)> """ يمكنك الآن التلاعب بقيم الوسطاء لتفهم أكثر. الآن سأستخدم لك هذه الطبقة في نموذج يحتوي على طبقة إدخال تقبل إدخال أبعاده 20 × 20 × 3 ، ثم طبقة كثيفة تليها طبقة تلافيفية تليها طبقة تجميع قصوى ، ثم طبقة تلافيفية أخرى ، تليها طبقة مخرجات.، ونظراً لأن الطبقات التلافيفية هنا ثنائية الأبعاد ، فإننا نستخدم طبقة MaxPooling2D من Keras ، لكن Keras لديها أيضًا طبقات تجميع 1d و 3 d max أيضاً.: import keras from keras.models import Sequential from keras.layers import Activation from keras.layers.core import Dense, Flatten from keras.layers.convolutional import * from keras.layers.pooling import * # بناء نموذج model_valid = Sequential([ # الدخل هو صورة بأبعاد 20 ب 20 و 3 قنوات لونية أي صورة ملونة Dense(16, input_shape=(20,20,3), activation='relu'), Conv2D(32, kernel_size=(3,3), activation='relu', padding='same'), MaxPooling2D(pool_size=(2, 2), strides=2, padding='valid'), Conv2D(64, kernel_size=(5,5), activation='relu', padding='same'), Flatten(), Dense(2, activation='softmax') ]) # هكذا سيكون شكل النموذج """ _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_2 (Dense) (None, 20, 20, 16) 64 _________________________________________________________________ conv2d_1 (Conv2D) (None, 20, 20, 32) 4640 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 10, 10, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 10, 10, 64) 51264 _________________________________________________________________ flatten_1 (Flatten) (None, 6400) 0 _________________________________________________________________ dense_2 (Dense) (None, 2) 12802 ================================================================= Total params: 68,770 Trainable params: 68,770 Non-trainable params: 0 _________________________________________________________________ """ الدخل والخرج: نعود الآن إلى الوسيط الرابع هو data_format هذا الوسيط يحدد ترتيب الأبعاد في المدخلات. يأخذ قيمتين إما channels_last وهي الحالة الافتراضية أي أن آخر وسيط في الإدخال سيمثل عدد القنوات اللونية في الصورة، أو channels_first أي ستكون في البداية، وعلى هذه الأساس سيختلف شكل الإدخال والإخراج لطبقتك : # الدخل data_format='channels_last': 4D tensor with shape (batch_size, rows, cols, channels). data_format='channels_first': 4D tensor with shape (batch_size, channels, rows, cols). # الخرج data_format='channels_last': 4D tensor with shape (batch_size, pooled_rows, pooled_cols, channels). data_format='channels_first': 4D tensor with shape (batch_size, channels, pooled_rows, pooled_cols).

يمكنك استخدام السلسلة الفارغة أو -1 فكلاهما نفس المعنى هنا. السلسلة الفارغة (أو -1 كما أشارت ريم) تعني أنه لايوجد أجهزة GPU (حتى ولو كانت موجودة) أي أنت تخفيها عنه لكي لايستخدمها. لذا لاداعي للتصحيح فلايوجد خطأ، انظر مثلاً: import os os.environ["CUDA_VISIBLE_DEVICES"] = "" import tensorflow as tf from tensorflow.python.client import device_lib print(device_lib.list_local_devices()) # عرض الأجهزة المتوفرة """ [name: "/device:CPU:0" device_type: "CPU" memory_limit: 268435456 locality { } incarnation: 5719422577836377687 ] """ أما وضع 0 أو 1 أو 2 (أعداد صحيحية موجبة) فهي تحدد أجهزة ال GPU التي تريد جعلها مرئية فالأجهزة التي يوجد فهرسها في التسلسل هي فقط الأجهزة المرئية لتطبيقات CUDA ويتم تعدادها بترتيب التسلسل، وإذا كان أحد الفهارس غير صالح، فلن تظهر لتطبيقات CUDA سوى الأجهزة التي يسبق فهرسها الفهرس غير الصحيح. أي مثلاً: لو ضبطتها بالشكل التالي 0,2,-1,1، فهذا يعني أن الجهاز الذي ترتيبه 0 و 2 سيكونان مرئيان لكن عندما يصل ل -1 (فهرس غير صالح أو غير موجود) فهنا سيتجاهله ويتجاهل مابعده أي سيتجاهل الجهاز ذو الفهرس 1 ولن يراه. حتى بالنسبة للإصدارات المختلفة فلا يوجد فرق في التعليمات. ,والتعليمة os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID" ليس لها علاقة بنسخة كيراس أو ويندوز وإنما هي المنهجية التي سيتم فيها ترتيب ال GPU التي لديك.

قم بوضع الكود التالي قبل استيراد tensorflow import os os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID" os.environ["CUDA_VISIBLE_DEVICES"] = "" أو قم بتشغيل السكريبت كالتالي : $ CUDA_VISIBLE_DEVICES="" ./code.py

إن طبقة ال LSTM الثانية الخاصة بك تقوم بإعادة كامل التسلسل أي خرجها 3D وذلك بسبب ضبط الوسيط return_sequences=True على True والطبقات الكثيفة Dense بشكل افتراضي تقوم بتطبيق kernel على كل خطوة زمنية أيضاً مما ينتج عنه تسلسل: # (batchsize, 50, 2) model.add( LSTM( 1024, input_shape=(50, 2), return_sequences=True)) # (batchsize, 50, 1024) model.add( LSTM( 200, return_sequences=True)) # (batchsize, 50, 200) model.add( (Dense(1))) # (batchsize, 50, 1) وهو الخرج الخاص بك لذا لحل المشكلة يجب عليك أن تقوم بالضبط التالي return_sequences=False في طبقة LSTM الثانية: import keras from keras.layers import Dense,LSTM import keras model = keras.Sequential() model.add( LSTM( 1024, input_shape=(50, 2), return_sequences=True)) model.add( LSTM( 200, return_sequences=False)) #(batchsize, 200) model.add( (Dense(1,activation=None))) #(batchsize, 1) model.compile(optimizer='rmsprop',loss='mae') model.fit( X, y, batch_size = 64,epochs=15)

لاتستخدم And هنا، يمكنك استخدام: dists[(dists >= r) & (dists <= r+dr)] # أو dists[(np.where((dists >= r) & (dists <= r + dr)))] لأن & هو "element-wise and" أي يطبق عملية and على أطراف العلاقة بت بت (وهذا سبب تسمية هذه المعاملات ب bitwise). إن np.where تعيد قائمة من الفهارس وليس مصفوفة بوليانية، وأنت تحاول استخدام and مع مصفوفتين من الأرقام (ليست قيم بوليانية). وبالتالي إذا كنت x و y كلاهما True فهذا يعني أن a and b=b: [0،3،6] and [2،5،4]=[2،5،4] لاحظ معي: ##################################################################### dists = np.arange(0,8,.7) r = 5 dr = 1 np.where(dists >= r) #(array([ 8, 9, 10, 11], dtype=int64),) np.where(dists <= r+dr) #(array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype=int64),) np.where(dists >= r) and np.where(dists <= r+dr) #(array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype=int64),) ##################################################################### # أما الذي كنت تتوقع مقارنته هو مصفوفة منطقية، على سبيل المثال dists >= r #array([False, False, False, False, False, False, False, False, True, True, True, True]) dists <= r + dr # array([ True, True, True, True, True, True, True, True, True, False, False, False]) (dists >= r) & (dists <= r + dr) # array([False, False, False, False, False, False, False, False, True, False, False, False]) يمكنك الآن استدعاء np.where على المصفوفة المنطقية المدمجة: dists[np.where((dists >= r) & (dists <= r + dr))]