-
المساهمات
1068 -
تاريخ الانضمام
-
تاريخ آخر زيارة
-
عدد الأيام التي تصدر بها
43
نوع المحتوى
ريادة الأعمال
البرمجة
التصميم
DevOps
التسويق والمبيعات
العمل الحر
البرامج والتطبيقات
آخر التحديثات
قصص نجاح
أسئلة وأجوبة
كتب
دورات
كل منشورات العضو Ali Haidar Ahmad
-
كما أجاب محمد، وأيضاً قد يكون الكود التالي جيداً لتحسين محركات البحث: <Link href="/timer" passHref> <Tab component="a" label="Timer" /> </Link> حيث أن Link لاتضيف href للابن حتى لو كان مكوناً. و passHref يفرض هذا، ولكن لا يمكن وضع منع PreventionDefault في onClick كما هو مذكور في توثيق MUI لأنه لن يغير عنوان URL.
- 2 اجابة
-
- 1
-

-
يجب عليك أن تقوم بتثبيت مكتبة Keras، ويمكنك القيام بذلك بعدة طرق: لكن قبل ذلك يجب أن تكون قد قمت بتثبيت كل من Numpy Pandas Scikit-learn Matplotlib Scipy Seaborn وتنسرفلو حيث أن كيراس تعتمد عليهم. ويمكنك تحميلهم جميعاً بنفس الطريقة التي سنثبت فيها كيراس الآن عن طريق استخدام مثبّت Python PIP، لذا سنقوم بالذهاب إلى Anaconda prompt وتشغيله من خلال الذهاب إلى قائمة إبدأ وكتابة Anaconda prompt ، ثم اكتب: pip install keras في حال استخدامك لينوكس أضف sudo قبل pip: sudo pip install keras ويمكنك تثبيتها من جوبيتر مباشرةً من خلال كتابة التعليمة pip install keras ضمن أي خلية ثم نفذ run. كما ويمكنك أيضاً أن تثبت كيراس عن طريق فتح الأناكوندا ثم إذهب إلى Anaconda Environment ثم ابحث عن keras package ثم ثبته install. وفي حال كنت تستخد كولاب فقط أضف إشارة ! قبل pip أي يصبح: !pip install keras
-
في بايثون، يتم التعامل مع ال arrays كمتجهات Vectors. أيضاً تسمى ال 2D-Arrays بال matrices. وهناك توابع جاهزة لتنفيذ الضرب بينهما في بايثون. وهما @ وتمثل التابع __matmul__ و numpy.dot وهما متشابهين جداً مع بعض الاختلافات. حيث تستخدم الدالة numpy.dot لإجراء ضرب المصفوفات matrices في بايثون (الضرب العادي) حيث يتحقق فيما إذا كان شرط ضرب المصفوفات محقق أولاً، أي أن عدد أعمدة المصفوفة الأولى يجب أن يكون مساوياً لعدد صفوف المصفوفة الثانية. ويعمل مع مصفوفات متعددة الأبعاد أيضاً. يمكننا أيضاَ تحديد مصفوفة بديلة كمعامل لتخزين النتيجة. المعامل @ يستدعي دالة __matmul__ لمصفوفة تُستخدم لإجراء نفس عملية الضرب. فمثلاً: # لاحظ كيف أعطيانا نفس الناتج import numpy as np a1 = np.array([[3,5],[0,3]]) a2 = np.array(([4,1],[6,7])) print(a1@a2) """ [[42 38] [18 21]] """ print(np.dot(a1,a2)) """ [[42 38] [18 21]] """ لكن عندما نتعامل مع المصفوفات متعددة الأبعاد ndArrays تكون النتيجة مختلفة قليلاً. يمكنك أن ترى الفرق في المثال: import numpy as np a1 = np.random.rand(2,2,2) a2 = np.random.rand(2,2,2) r1 = np.dot(a1,a2) r1 """ [[[[0.12022633 0.02387914] [0.01322726 0.14207161]] [[0.61570778 0.04646624] [0.66232634 0.33838594]]] [[[0.63522905 0.0644122 ] [0.55415297 0.43366682]] [[0.79912989 0.13910756] [0.2417268 0.84365592]]]] """ print(r1.shape) # (2, 2, 2, 2) r2 = (a1@a2) """ [[[0.12022633 0.02387914] [0.61570778 0.04646624]] [[0.55415297 0.43366682] [0.2417268 0.84365592]]] """ print(r2,r2.shape) # (2, 2, 2) حيث أن الدالة matmul تقوم بعملية "Brodcasting" على المصفوفة، أي يتم التعامل معها على أنها كومة من المصفوفات الموجودة في الفهرين الأخيرين ويتم بثها وفقاً لذلك. لكنها تحافظ على أبعاد الخرج أي : (n,k),(k,m)->(n,m) مثلاً: a = np.ones([9, 5, 7, 4]) c = np.ones([9, 5, 4, 3]) np.dot(a, c).shape #(9, 5, 7, 9, 5, 3) np.matmul(a, c).shape #(9, 5, 7, 3) # n is 7, k is 4, m is 3 ومن ناحية أخرى، تقوم الدالة numpy.dot بالضرب كمجموع حاصل الضرب على المحور الأخير من المصفوفة الأولى والثاني إلى الأخير من الثانية. هناك اختلاف آخر بينهما، وهو أن الدالة matmul لا يمكنها إجراء عملية ضرب للمصفوفة بقيم عددية: import numpy as np a = np.array([1, 2]) np.dot(a,5) # array([ 5, 10]) a@5 # ValueError: matmul: Input operand 1 does not have enough dimensions (has 0, gufunc core with signature (n?,k),(k,m?)->(n?,m?) requires 1)
- 2 اجابة
-
- 1
-

-
يتم استخدام الوظيفة لإجراء فرز غير مباشر على طول المحور المحدد باستخدام الخوارزمية المحددة له (تحدد له الخوارزمية التي ستقوم بالفرز مثل الفرز على أساس الكومة أو باستخدام مبدأ فرق تسد mergesort أو خوارزمية الفرز السريع). تقوم بإرجاع مصفوفة من الفهارس من نفس الشكل مثل arr التي من شأنها أن تفرز المصفوفة.لها الشكل التالي: numpy.argsort(arr, axis=-1, kind=’quicksort’, order=None) بحيث أن الوسيط الأول هو الصفوفة، والثاني هو المحور وإذا تم ضبطه على None ، فسيتم تسوية المصفوفة "flatten" قبل الفرز. وافتراضياً هي -1 ، أي يقوم بالفرز على أساس المحور الأخير. أما الوسيط الثالث فهو نوع الخوارزمية [‘quicksort’, ‘mergesort’, ‘heapsort’] وافتراضياً هي quicksort. أما الوسيط الأخير فيستخدم عندما تكون المصفوفة عبارة عن مصفوفة ذات حقول محددة، حيث تحدد هذه الوسيطة الحقول المراد مقارنتها أولاً ، وثانيًا ، وما إلى ذلك. وتعيد هذه الدالة مصفوفة من الفهارس التي تفرز مصفوفتك على طول المحور المحدد. أمثلة: import numpy arr = numpy.array([ 3, 5, 1, 5, 4, 1]) print (arr) # [3 5 1 5 4 1] sorted = numpy.argsort(arr) print ("Output sorted array indices : ", sorted) print("Output sorted array : ", arr[sorted]) #Output sorted array indices : [2 5 0 4 1 3] #Output sorted array : [1 1 3 4 5 5] ########################################################################## import numpy arr = numpy.array([[ 5, 6], [4, 3]]) print (arr) """ [[5 6] [4 3]] """ # هنا حددنا خوارزمية فرق تسد # حددنا أيضاً الفرز على المحور العمودي sorted = numpy.argsort(arr, kind ='mergesort', axis = 0) print ("Output sorteded array indices along axis 0: \n", sorted) """ Output sorteded array indices along axis 0: [[1 1] [0 0]] """ # هنا غيرنا بالخوارزمية والمحور sorted2 = numpy.argsort(arr, kind ='heapsort', axis = 1) print ("Output sorteded array indices along axis 1: \n", sorted2) """ Output sorteded array indices along axis 1: [[0 1] [1 0]] """ ويمكنك استخدامها للتريب التنازلي أيضاً وتجد ذلك في الرابط التالي:
- 3 اجابة
-
- 1
-

-
من أحدث دوال التنشيط، ظهرت حوالي عام 2017، مع 90 صفحة من البراهين، ,وهي معقدة إلى حد ما مقارنة بباقي دوال التنشيط، شكلها العام كما يلي (يمكنك الإطلاع على شكلها البياني في الإجابة المقدمة من Ahmed Sharshar -البيان الأول-) : if x > 0: return scale * x if x < 0: return scale * alpha * (exp(x) - 1) # بحيث # alpha=1.67326324 # scale=1.05070098 إذا كانت قيمة الإدخال x أكبر من الصفر ، فإن قيمة المخرجات تصبح x مضروبة في lambda λ أو scale.أما إذا كانت قيمة الإدخال x أصغر أو تساوي الصفر، يتشكل لدينا منحني على طول المحور السالب بحيث يرتفع إلى 0 عندما يكون x صفر. بشكل أساسي. وهذا مايعطي الدالة القدر على التعلم وبشكل فعال من أجل أي دخل. شيئ آخر جدير بالذكر عن هذه الدالة هو أنها تقوم بعملية normalization إلى حد ما للبيانات (كما أشار Ahmed Sharshar). ويشار لها بأنها تحقق مبدأ "self-normalizing neural networks". وهذا مايعطي الشبكة سرعة أكبر. (في الرابط في الأسفل شرح لل Batch normlaization). عند التحدث عن أي دالة تنشيط فإن أهم ماتريده هو المشتقات، فهي محور عملية التعلم والتدريب، هذه الدالة على محورها الموجب مطابقة لدالة elu إلا أنها تضيف عليها تحسيناً وهو ضربها بمعامل scale (أو يشار له بلمدا وقيمته حصراً أكبر من واحد) والغاية من ذلك جعل الميل أكبر من 1 وبذلك تجعل قيمة المشتق على هذا المجال دوماً أكبر من واحد وهذا يجعل عملية التعلم أسرع. وعلى المحور السالب تكون قيم المشتق كما في الرسم البياني الثاني في إجابة Ahmed Sharshar وبالتالي قابلية للتعلم على المحور السالب أيضاً وبكفاءة. هذا يجعلها تحل كل المشاكل التي تعاني منها بقية توابع التنشيط (في الرابط في الأسفل تجد دالة ال elu وكل مايتعلق بهذه المشاكل). لكن مشكلتها أنه لم يصدر أي أوراق بحثية فيما إذا كانت جيدة للتطبيق مع الشبكات العصبية المتكررة RNNs و التلاففية CNNs. في كيراس تجدها في الموديول التالي: tf.keras.activations.selu(x) ولاستخدامها أثناء تدريب نماذجك يمكنك تمريرها للطبقة بإحدى الطرق في المثال التالي: model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='selu'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.elu,kernel_initializer='lecun_normal')) أو بالشكل التالي model.add(Dense(64,kernel_initializer='lecun_normal')) model.add(Activation(activations.selu )) # أو model.add(Activation("selu")) lecun_normal ومن الضروري تهيئة الأوزان في الطبقة التي تستخدم فيها هذه الدالة بالتوزيع """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary() وطبعاً توحيد ال Input features بمتوسط 0 وانحراف معياري 1 يكون مضمون من خلال قيمتي ألف و لمدا (هذه القيم تم اختيارها مسبقاً) ومن خلال استخدام المهيئ المناسب وهو lecun_normal.
-
هذه الدالة هي اختصار ل Exponential Linear Unit إن هذه الدالة تشبه كثيراً الدالة RelU التي تحدثت عنها في إجابة سابقة سأضع رابطها في الأسفل. هذه الدالة شكلها البياني تجده في الرسم البياني الأول الذي قدمه Ahmed Sharsha. كما تلاحظ فإن هذه الدالة تشبه إلى حد كبير دالة ال relu. وذلك على المجال من 0 للانهاية+ ، وهذه الدالة لاتعاني من مشاكل ال vanishing gradients و exploding gradients أي تلاشيي وإنفجار المشتقات وهذا لأنها لاتعاني من مشكلة تشبع الخلايا (المشكلة التي تعاني منها دالة السيني وال tanh). وأيضاً تتميز عنها بأنها لاتعاني من مشكلة ال dying neurons (موت الخلايا) لأن قيم مشتقانه غير معدومة في أي نقطة من المجال السالب (على عكس ريلو التي تنعدم فيه المشتقات على الجزء السالي). ففي دالة الريلو تكون القيمة دوماً 0 على القيم السالبة للدخل، وبالتالي إذا كانت الخلايا دخلها 0 سيؤدي ذلك إلى مشتقات صفرية وتوقف عملية التعلم (طالما لم تدفع المدخلات الدالة ReLU إلى الجزء السلبي (أي أن بعض المدخلات ضمن المجال الموجب) ، يمكن للخلايا العصبية أن تظل نشطة ، ويمكن تحديث الأوزان، ويمكن للشبكة مواصلة التعلم). يؤدي استخدام ELU إلى أوقات تدريب أقل ودقة أعلى في الشبكات العصبية مقارنة بـ ReLU وأخواته (PReLU-LReLU-). وكما ترى من الرسم البياني فإن هذه الدالة مستمرة وقابلة للاشتقاق عند كل النقاط وقيم مشتقاتها تساوي ال 1 في أي نقطة من الجزء الموجب وبالتالي تمنحك سرعة في عملية التعلم، إضافة إلى أنها لاتنعدم على الجزء السالب أي أنها تمنح الخلايا القدرة على التعلم في الجزء السالب للدخل أيضاً حيث تكون قيمة المشتقة في أي نقطة سالبة هي exp (x).ولها الشكل التالي: y = ELU(x) = exp(x) − 1 ; if x<0 y = ELU(x) = x ; if x≥0 كما أنها تحقق دقة أعلى مقارنة بوظائف التنشيط الأخرى مثل ReLU و Sigmoid و Hyperbolic Tangent. لكن يجب أن نعلم أن سرعتها خلال وقت الاختبار تكون أبطأ من relu وأخواتها، وتعقيدها الحسابي أكبر منهم أيضاً وهذا هو عيبها مقارنة بهم. وفي كيراس لها لشكل التالي: tf.keras.layers.ELU(alpha=1.0) بحيث: f(x) = alpha * (exp(x) - 1.) for x < 0 f(x) = x for x >= 0 لاحظ أنه في كيراس يتم إضافة معامل نسميه ألفا للتحكم بالقيم الناتجة في المجال السلبي. ولاستخدامها أثناء تدريب نماذجك يمكنك تمريرها للطبقة بإحدى الطرق في المثال التالي: model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='elu'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.elu)) أو بالشكل التالي model.add(Dense(64)) model.add(Activation(activations.elu )) # أو model.add(Activation("elu ")) """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary()
-
ترتيب الأبعاد لديك في طبقة الإدخال غير صحيح وهذا هو سبب الخطأ في نموذجك. ركز معي ... غالباً عندما نتعامل مع الصور فإننا نكون على دراية بطول وعرض الصور وإذا كانت ملونة (3 قنوات لونية) أم رمادية (قناة لونية واحدة)، لكن مالانعلمه غالباً هو ترتيب الأبعاد، وهناك حالتين: الأولى هي Channels Last: وهنا يتم تمثيل بيانات الصورة في مصفوفة ثلاثية الأبعاد حيث تمثل القناة الأخيرة قنوات الألوان ، أي يكون ترتيب الأبعاد [صفوف] [أعمدة] [عدد القنوات اللونية]. والثانية هي Channels First وفي هذه الحالة يتم تمثيل بيانات الصورة في مصفوفة ثلاثية الأبعاد حيث يمثل البعد الأول عدد القنوات اللونية، أي يكون ترتيب الأبعاد [عدد القنوات اللونية] [صفوف] [أعمدة]. الآن عندما نقوم بتحديد أبعاد طبقة الإدخال input shape، يجب أن نعرف هذا الترتيب. ونقوم بذلك في كيراس من خلال backend.image_data_format بالشكل التالي من خلال : from keras import backend img_height,img_width=100,100 num_chaneel=3 if backend.image_data_format() == 'channels_last': # image_data_format() تعطيك النمط input_s=(img_height,img_width,num_chaneel) else: input_s=(num_chaneel,img_height,img_width) ونعدل طبقة الإدخال: model = Sequential() #1st Convolutional Layer model.add(Conv2D(64, (3, 3), input_shape=input_s)) ويمكنك معرفته من خلال قراءة إحدى الصور كمصفوفة وعرض أبعادها من خلال الواصفة shape. كالتالي: img = cv2.imread(yourpath) print(img.shape) # (100, 100, 3) هنا يمكنك أن تلاحظ أن أبعادها (100,100,3) أي أنها تتبع النمط Channels Last، وبالتالي يجب أن نتقيد بهذا الترتيب في طبقة الإدخال أي يجب أن يكون input_shape=(100,100,3) وهنا طريقة أخرى باستخدام mpimg: import matplotlib.image as mpimg img = mpimg.imread(yourPath) img.shape # (100, 100, 3) أو من خلال PIL: from PIL import Image img = Image.open(yourpath) img.shape
-
في هكذا حالات نستخدم قناع، أولاً تأمل الفكرة التالية: import numpy as np a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) #للعنصر الذي نريده أن يظهر True ننشئ قناع بالحجم الذي نريده ونضع mask=[True,True,True,True,True,False,True,True,True] #False الآن ستظهر كل عناصر المصفوفة ماعدا العنصر الذي وضعنا له a[mask] #array([1, 2, 3, 4, 5, 7, 8, 9]) # 6 غير موجودة حسناً هناك طريقة أكثر راحة لإنشاء القناع كالتالي: import numpy as np a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) mask = np.ones(a.shape, bool) mask # array([ True, True, True, True, True, True, True, True, True]) a[mask] #array([1, 2, 3, 4, 5, 6, 7, 8, 9]) الآن يمكننا تطبيق الفكرة السابقة لاستبعاد أي فهرس نريده: #فقط في القناع False الآن لو أردنا استبعاد عنصر نقوم بوضع # مثلاً أريد استبعاد الفهرس 6 exclude=5 mask[exclude] = False a[mask] # array([1, 2, 3, 4, 5, 7, 8, 9]) هناك طريقة أخرى وهي الأسهل وتتمثل باستخدام الدالة delete حيث نمرر لها فهرس العنصر المراد استبعاده، وطبعاً لاتؤثر على العنصر الفعلي الموجود في المصفوفة لأن هذه الدالة ترجع نسخة من المصفوفة وبالتالي التعديل لايتم على المصفوفة الأصلية: import numpy as np a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # مثلاً أريد استبعاد الفهرس 6 exclude=6 np.delete(a, exclude) # array([1, 2, 3, 4, 5, 6, 8, 9]) كذلك يمكنك استخدام np.isin ، لتوليد القناع، لكن دعنا نفهم ماتقوم به هذه الدالة أولاً: import numpy as np a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # numpy.isin(element, test_elements) #في مكان العنصر المراد True هذه الدالة تأخذ مصفوفة + العنصر المراد البحث عنه، وخرجها يكون مصفوفة بنفس الأبعاد لكن تضع #في باقي الأماكن False و np.isin(a, 6) # array([False, False, False, False, False, True, False, False, False]) # وبالتالي لو قمنا بعملية نفي على قيم المصفوفة سيكون الخرج ~np.isin(a, 6) # array([ True, True, True, True, True, False, True, True, True]) # وهذه الفكرة سنستخدمها لإنشاء القناع والحل يكون خطوة بخطوة: a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) b=np.ones(len(a)) # array([1., 1., 1., 1., 1., 1., 1., 1., 1.]) # مثلاً أريد استبعاد الفهرس 6 exclude=6 # أحول المصفوفة السابقة لقناع بولياني ~np.isin(b, exclude) # array([ True, True, True, True, True, True, False, True, True]) a[~np.isin(b, exclude)] # array([1, 2, 3, 4, 5, 6, 8, 9]) # واختصاراً # a[~np.isin(np.arange(len(a)), exclude)] وبنفس الطريقة نستخدم np.in1d: import numpy as np a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) a # array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # مثلاً أريد استبعاد الفهرس 6 exclude=6 a[~np.in1d(np.arange(len(a)), exclude)] # array([1, 2, 3, 4, 5, 6, 8, 9])
- 4 اجابة
-
- 1
-

-
import math import numpy import scipy # من ناحية نمط البيانات type(numpy.pi)==type(math.pi)==type(scipy.pi) # True # القيمة math.pi == np.pi == scipy.pi # True 3.141592653589793 # نجد اختلاف بسيط من ناحية الأداء %timeit scipy.pi*1000 """ The slowest run took 36.02 times longer than the fastest. This could mean that an intermediate result is being cached. 10000000 loops, best of 5: 102 ns per loop """ %timeit numpy.pi*1000 """ The slowest run took 27.30 times longer than the fastest. This could mean that an intermediate result is being cached. 10000000 loops, best of 5: 107 ns per loop """ %timeit math.pi*1000 """ The slowest run took 23.38 times longer than the fastest. This could mean that an intermediate result is being cached. 10000000 loops, best of 5: 94.2 ns per loop """ ووجودها في 3 مكتبات يسهل عليك العمل، فمثلاً اعتبر أنها غير موجودة في نمباي وأنت الآن تتعامل مع مصفوفات نمباي وتريد استخدام هذه القيمة، وبالتالي ستكون مجبراً على استيرادها من الوحدة math أو scipy. لذا فإن وجودها في نفس المكتبة التي تعمل بها يريحك من عملية استيرادها عند الحاجة.
- 3 اجابة
-
- 1
-

-
يمكنك القيام بذلك من خلال الدالة np.repeat بالشكل التالي، حيث تدرج الفهرسة باستخدام np.newaxis بُعدًا ثالثًا جديدًا، نكرره بعد ذلك مع المصفوفة: import numpy as np arr = np.array([[1, 2], [1, 2]]) arr.shape # (2, 2) a = np.repeat(arr[:, :, np.newaxis], 3, axis=2) arr.shape # (2, 2, 3) print(a[:, :, 0]) """ [[1 2] [1 2]] """ print(a[:, :, 1]) """ [[1 2] [1 2]] """ print(a[:, :, 2]) """ [[1 2] [1 2]] """ a """ array([[[1, 1, 1], [2, 2, 2]], [[1, 1, 1], [2, 2, 2]]]) """ أو: import numpy as np arr = np.array([[1, 2], [1, 2]]) arr.shape # (2, 2) a = np.repeat(arr[np.newaxis,:, :], 3, axis=0) # حددنا المحور العمودي للتكرار arr.shape # (2, 2, 3) print(a[0,:, :]) """ [[1 2] [1 2]] """ print(a[1,:, :]) """ [[1 2] [1 2]] """ print(a[2,:, :]) """ [[1 2] [1 2]] """ a """ array([[[1, 2], [1, 2]], [[1, 2], [1, 2]], [[1, 2], [1, 2]]]) """ أو من خلال دالة np.broadcast_to حيث أن هذه الطريقة لاتتطلب منك ذاكرة إضافية أبداً: import numpy as np arr = np.array([[1, 2], [1, 2]]) arr.shape # (2, 2) numofrepeats = 3 # إذا أردت التكرار على المحور العمودي np.broadcast_to(arr,(numofrepeats,)+arr.shape) """ array([[[1, 2], [1, 2]], [[1, 2], [1, 2]], [[1, 2], [1, 2]]]) """ # على المحور الثالث np.broadcast_to(arr[...,None],arr.shape+(numofrepeats,)) """ array([[[1, 1, 1], [2, 2, 2]], [[1, 1, 1], [2, 2, 2]]]) """
-
هذه الدالة هي اختصار ل Exponential Linear Unit إن هذه الدالة تشبه كثيراً الدالة RelU التي تحدثت عنها في إجابة سابقة سأضع رابطها في الأسفل. هذه الدالة لها الشكل التالي: كما تلاحظ فإن هذه الدالة تشبه إلى حد كبير دالة ال relu. وذلك على المجال من 0 للانهاية+ ، وهذه الدالة لاتعاني من مشاكل ال vanishing gradients و exploding gradients أي تلاشيي وإنفجار المشتقات وهذا لأنها لاتعاني من مشكلة تشبع الخلايا (المشكلة التي تعاني منها دالة السيني وال tanh). وأيضاً تتميز عنها بأنها لاتعاني من مشكلة ال dying neurons (موت الخلايا) لأن قيم مشتقانه غير معدومة في أي نقطة من المجال السالب (على عكس ريلو التي تنعدم فيه المشتقات على الجزء السالي). ففي دالة الريلو تكون القيمة دوماً 0 على القيم السالبة للدخل، وبالتالي إذا كانت الخلايا دخلها 0 سيؤدي ذلك إلى مشتقات صفرية وتوقف عملية التعلم (طالما لم تدفع المدخلات الدالة ReLU إلى الجزء السلبي (أي أن بعض المدخلات ضمن المجال الموجب) ، يمكن للخلايا العصبية أن تظل نشطة ، ويمكن تحديث الأوزان ، ويمكن للشبكة مواصلة التعلم). يؤدي استخدام ELU إلى أوقات تدريب أقل ودقة أعلى في الشبكات العصبية مقارنة بـ ReLU وأخواته (PReLU-LReLU-). وكما ترى من الرسم البياني فإن هذه الدالة مستمرة وقابلة للاشتقاق عند كل النقاط وقيم مشتقاتها تساوي ال 1 في أي نقطة من الجزء الموجب وبالتالي تمنحك سرعة في عملية التعلم، إضافة إلى أنها لاتنعدم على الجزء السالب أي أنها تمنح الخلايا القدرة على التعلم في الجزء السالب للدخل أيضاً حيث تكون قيمة المشتقة في أي نقطة سالبة هي exp (x).ولها الشكل التالي: y = ELU(x) = exp(x) − 1 ; if x<0 y = ELU(x) = x ; if x≥0 كما أنها تحقق دقة أعلى مقارنة بوظائف التنشيط الأخرى مثل ReLU و Sigmoid و Hyperbolic Tangent. لكن يجب أن نعلم أن سرعتها خلال وقت الاختبار تكون أبطأ من relu وأخواتها، وتعقيدها الحسابي أكبر منهم أيضاً وهذا هو عيبها مقارنة بهم. وفي كيراس لها لشكل التالي: tf.keras.layers.ELU(alpha=1.0) بحيث: f(x) = alpha * (exp(x) - 1.) for x < 0 f(x) = x for x >= 0 لاحظ أنه في كيراس يتم إضافة معامل نسميه ألفا للتحكم بالقيم الناتجة في المجال السلبي. ولاستخدامها أثناء تدريب نماذجك يمكنك تمريرها للطبقة بإحدى الطرق في المثال التالي: هي دالة تنشيط تستخدم مع الشبكات العصبية وتعطي خرجاً ضمن المجال 1 ل -1. ولها الشكل التالي: softsign(x) = x / (abs(x) + 1). حسناً هذه الدالة مرتبطة ارتباطاً وثيقاً بدالة tanh لذا أنصح أولاً بقراءة مافي الرابط التالي: فهذه الدالة جاءت بغاية تطوير أو تحسين دالة ال tanh بغية منع الخلايا من الوصول لحالة ((التشبع)) بسرعة. أي بمعنى آخر منع الخلايا من الوصول لحالة عدم القدرة على تعلم أي معلومات جديدة. الآن تأمل الرسم البياني التالي، حيث أن الخط الأزرق يمثل دالة ال tanh واللون البرتقالي يمثل مشتقها واللون الأحمر هو دالة ال softsign والأخضر مشتقها. Untitled.png.fbd860c09a00b8701770efc197487751.png كما تلاحظ فإن دالة التانش تتقارب بشكل سريع من المقارب الأفقي (القيمة y=1 و y=-1) حيث أنها تتقارب منهم بشكل أسي، وهذا مايؤثر سلباً على قيم المشتق حيث أن ميل المماس يصبح أفقياً بسرعة كبيرة مع زيادة قيم ال x وهذا مايعني أن قيم المشتقة تنخفض وهذا مايعني أن عملية التعلم تتباطأ أسياً حتى تنعدم تقريباً في حالة استمرار تزايد قيمة قيم الدخل وهذا مانسميه بحالة (التشبع) أي أن الخلايا لم تعد قاردة على التعلم من البيانات أكثر من ذلك وهذا واضح جداً من الرسم جانباً حيث أن دالة المشتق للتانش تتقارب سريعاً من الصفر. الآن لو نظراً لدالة السوفت فإن أول أمر يمكننا ملاحظته هو أن دالة السوفت كما يشير اسمها هي دالة أنعممم والمقصود هنا أن دالة المشتق لها تتقارب ولكنها لاتنعتدم بسرعة كما في ال tanh وبالتالي منع الخلايا من التشبع. وهي الميزة الوحيدة لها مقارنة بال tanh أما على الجانب الآخر فنجد أن قيم المشتق للتانش أكبر ضمن مجال الدخل من -1 ل 1 وهذا أفضل لعملية التعلم. وفي كيراس يمكننا أن نجدها ضمن الموديول التالي: tf.keras.activations.softsign(x) ولاستخدامها أثناء تدريب نماذجك يمكنك تمريرها للطبقة بإحدى الطرق في المثال التالي: model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='elu'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.elu)) أو بالشكل التالي model.add(Dense(64)) model.add(Activation(activations.elu )) # أو model.add(Activation("elu ")) """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary()
-
يمكنك أولاً استخدام التابع bincount حيث أن هذا التايع يقوم بحساب عدد مرات التكرار لكل عنصر من المصفوفة: import numpy as np array = np.array([2, 9, 7, 10,3, 5, 3]) count=np.bincount(array) count # array([0, 0, 1, 2, 0, 1, 0, 1, 0, 1, 1]) # لاحظ أنه يعيد مصفوفة عدد عناصرها يساوي أكبر عنصر في المصفوفة # مثلاً في مصفوفتنا السابقة أكبر عنصر هو 10 وبالتالي سيكون حجم المصفوفة الناتجة10 # من المصفوفة الناتجة نستنتج أن العنصر الأكثر ظهوراً هو 3 حيث أن القيمة التي تقابل الفهرس 3 تساوي 2 في المصفوفة الناتجة أي أنه ظهر مرتين الآن يمكننا استخدام النتيجة التي حصلنا عليها من هذا التابع لمعرفة العنصر ذو أعلى تردد (الأكثر ظهوراً) ضمن المصفوفة وذلك من خلال التابع Argmax حيث يرد هذا التابع فهرس العنصر الأكبر، وفي المصفوفة count فإن العنصر الأكبر هو 2 وهو يقابل الفهرس 3 وهو يقابل أو يمثل القيمة 3 في المصفوفة Array: count.argmax() # 3 لكن مهلاً، بفرض كان هناك عنصران لهم أعلى ظهور ماذا سيحدث؟ import numpy as np array = np.array([2, 9, 7, 10,3,2, 5, 3]) count=np.bincount(array) count # array([0, 0, 2, 2, 0, 1, 0, 1, 0, 1, 1]) count.argmax() # 2 !!! لن يعطيك سوى قيمة وحيدة لاحظ أن العنصر 3 و العنصر 2 ظهرا مرتين لكن بهذه الطريقة لن نحصل إلا على قيمة واحدة. لذا الحل يكون كالتالي: maximum = max(count) #count نحسب القيمة الأكبر في مصفوفة ال #وكلما رأينا القيمة 2 نطبع الفهرس المقابل لها count نمرر حلقة على مصفوفة ال for i in range(len(count)): if count[i] == maximum: print(i, end=" ") # 2 3 الآن يجب أن تضع في حسبانك أن هذه الدالة تعمل فقط مع الأعداد، فماذا بشأن ال string وغيرها؟؟... هنا يأتي دور الدالة counter، كما ويمكنها حل مشكلتك مع الأرقام كالتالي: from collections import Counter array = np.array([2, 9,9, 7, 10,3, 5, 3]) array # array([ 2, 9, 9, 7, 10, 3, 5, 3]) # ترد هذه الدالة قاموس مفاتيحه هي العناصر وقيمها هي عدد مرات الظهور c = Counter(array) c # Counter({2: 2, 3: 2, 5: 1, 7: 1, 9: 1, 10: 1}) #مرتبة بحيث تكون العناصر الأكثر تكراراً في البداية tuble نطبق عليها الدالة التالية والتي تقوم بتحويلها إلى قائمة من ال freq=c.most_common() print (freq) # [(9, 2), (3, 2), (2, 1), (7, 1), (10, 1), (5, 1)] # والآن يمكنك استخراجها بسهولة freq[0][0] # 9 # إذا أردنا إظهار 3 أيضاً for i in range(0,len(freq)): if freq[i][1]==freq[0][1]: print(freq[i][0], end=" ") # 9 3 هناك طريقة أخرى وهي استخدام Mode من scipy.stats وكما نعلم فإن ال Mode هو العنصر الأكثر تكراراً: from scipy import stats as s array = np.array([2, 9, 7, 10,3, 5, 3]) print(s.mode(array)[0]) # 3 # لكن في حالة وجدت قيمتين سيعطيك الخطأ التالي array = np.array([2, 9,9, 7, 10,3, 5, 3]) print(s.mode(array)[0]) # [3]
-
حسناً، يمكنك استخدام الدالة argsort لفرز المصفوفة، لكنها تقوم بعملية الفرز بشكل تصاعدي: import numpy as np array = np.array([2, 9, 7, 10, 5, 3]) a = np.sort(array) a # array([ 2, 3, 5, 7, 9, 10]) لذا لجعله تنازلياً، يمكنك استخدام الدالة numpy.flip عن طريق تمرير الدالة argsort لها حيث سترد لك ال indexes للقيم مرتبة بترتيب تنازلي بعد أن يتم فرزها تصاعدياً باستخدام argsort حيث تقوم هذه الدالة بعكس ترتيب العناصر : import numpy as np a = np.array([2, 9, 7, 10, 5, 3]) n=3 ids = np.flip(np.argsort(a)) print(ids[0:n]) #[3 1 2] نفس الفكرة باستخدام np.flipud: import numpy as np a = np.array([2, 9, 7, 10, 5, 3]) n=3 ids = np.flipud(np.argsort(a)) print(ids[0:n]) #[3 1 2] أو يمكنك القيام بعكسها بإحدى الأشكال التالية: # نضرب المصفوفة بسالب وبالتالي يصبح الأصغر أكبر وبالتالي نحصل على الفهرس المطلوب np.argsort(-1*a)[:3] #- كما ويمكن استخدام المعامل # أي بشكل مشابه للطريقة السابقة (-a).argsort()[:3] # أو بالطريقة التقليدية عن طريق أخذ آخر 3 عناصر a.argsort()[::-1][:3] وكمقارنة: %timeit np.flipud(np.argsort(a))[0:3] %timeit np.flip(np.argsort(a))[0:3] %timeit np.argsort(-1*a)[:3] %timeit (-a).argsort()[:3] %timeit a.argsort()[::-1][:3] 5.14 µs ± 211 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) 5.29 µs ± 337 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) 4.57 µs ± 127 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) 1.97 µs ± 288 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) 1.86 µs ± 251 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) # الطريقة الأخيرة أفضل
- 4 اجابة
-
- 1
-

-
حسناً دعنا نناقش كل شيء بشكل منفصل. أولاً دعني أعرفك كيف تقوم بإضافة عنصر أو عدة عناصر لمصفوفة في نمباي. أولاً لإضافة عنصر في نهاية القائمة نستخدم الدالة append كالتالي: # numpy.append(arr, values, axis=None) شكل الدالة # أول وسيط هو المصفوفة # ثاني وسيط هو القيمة # الثالث هو المحور الذي نريد إضافة العنصر له # تعيد هذه الدالة نسخة من المصفوفة تحوي العنصر أو العناصر المضافة import numpy as np a=np.array([1,2,3]) a=np.append(a,1) a # array([1, 2, 3, 1]) # لإضافة أكثر من عنصر a=np.append(a,[2,3]) a # array([1, 2, 3, 1, 2, 3]) # الآن لو جربنا إضافة مصفوفة ثنائية الأبعاد لها np.append(a,[[4, 5, 6], [7, 8, 9]]) # array([1, 2, 3, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # لاحظ كيف قام بتسطيح المصفوفة الثنائية ثم أضافها للمصفوفة وذلك لأننا لم نحدد له المحور # الآن سنحدد له المحور a # array([1, 2, 3, 1, 2, 3]) np.append(a,[[4, 5, 6], [7, 8, 9]],axis=0) # ValueError: all the input arrays must have same number of dimensions # أعطى خطأ لأن المصفوفتين يجب أن يكون لهما أبعاد متسقةأي نحن نريد أن نضيف المصفوفة الثنائية إلى المصفوفة الأصلية على المحور العمودي وبالتالي يجب أن تتطابق أبعاد الأعمدة # انظر arr=[[1, 2, 3], [4, 5, 6]] np.append([[1, 2, 3], [4, 5, 6]],[ [7, 8, 9]],axis=0) """ array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) """ الآن لو أردت إضافة عنصر في فهرس محدد من المصفوفة (أي أي مكان تريده في البداية أو النهاية أو الوسط ..) يمكنك استخدام الدالة insert: #numpy.insert(arr, obj, values, axis=None) import numpy as np #obj هو الفهرس أو الفهارس التي تريد أن تتم الإضافة عندها # تعيد نسخة أيضاً # مثلا تريد إضافة عنصر لنهاية المصفوفة a = np.asarray([1,2,3]) a=np.insert(a, 3, 1) a # array([1, 2, 3, 1]) # إذا كنت لاتعرف الفهرس الخاص بآخر عنصر a = np.asarray([1,2,3]) np.insert(a, len(a), 1) # len(a)=3 حيث ترد لك عدد العناصر في المصفوفة # array([1, 2, 3, 1]) ########################## مثال آخر ######################## a = np.array([[1, 1], [2, 2], [3, 3]]) a """ array([[1, 1], [2, 2], [3, 3]]) """ #append هنا لم نحدد له المحور وبالتالي الإضافة تكون كما في np.insert(a, 1, 5) # array([1, 5, 1, 2, 2, 3, 3]) # هنا حددنا المحور الأفقي np.insert(a, 1, 5, axis=1) """ array([[1, 5, 1], [2, 5, 2], [3, 5, 3]]) """ #brodcasting لاحظ كيف تم تنفيذ عملية نسخ وهذه عملية نسميها # الآن لاحظ حالة ثانية عندما نحدد أكثر من قيمة أي نريد أن نضيف عدة قيم في الفهرس1 على طول المحور np.insert(a, [1], [[1],[2],[3]], axis=1) """ rray([ [1, 1, 1], [2, 2, 2], [3, 3, 3]]) """ استخدام الدالة concatenate لهكذا أمر هو تكنيك غير شائع فالدالتين السابقتين ستغنينك عن أي طريثة أخرى، لكنني سأوضح لك استخدامها: # numpy.concatenate((a1, a2, ...), axis=0) # ربط سلسلة من المصفوفات على طول محور موجود # (a1, a2, ...) تسلسل من المصفوفات # يجب أن يكون للمصفوفات نفس الشكل ، إلا في البعد المقابل للمحور (الأول ، افتراضيًا) a1 = np.array([[1, 2], [3, 4]]) # shape: 2*2 """ array([[1, 2], [3, 4]]) """ a2 = np.array([[5, 6]]) # shape: 1*2 # الأبعاد متناسقة إذا أردنا إضافة المصفوفة الثانية للأولى على المحور العمودي np.concatenate((a1, a2), axis=0) """ array([[1, 2], [3, 4], [5, 6]]) """ # على المحور الأفقي الأبعاد غير متناسقة وبالتالي سيظهر خطأ لو حاولنا الإضافة لذا يجب أن نقوم بتعديل أبعاد المصفوفة وهذا سهل في حالتنا a2=a2.T # shape: 2*1 a2 """ array([[5], [6]]) """ np.concatenate((a1, a2), axis=1) """ array([[1, 2, 5], [3, 4, 6]]) """ #################################################### وأخيراً سبب الخطأ لديك أعتقد ستكون استنتجته ينفسك، فالسبب هو أنك تقوم بمحاولة ربط مصفوفة بقيمة، لكن دالة concatenate كما ذكرت لك في الكود في الأعلى تأخذ سلسلة من المصفوفات وليس القيم، وبالتالي يظهر لك الخطأ، وبالتالي لحل مشكلتك يمكنك وضع القيمة بمصفوفة وسينجح الأمر: type(a[0]) # numpy.int64 وهي ماتعتبر أبعاد صفرية وبالتالي لن ينجح في مطابقة الأبعاد وسيعطيك خطأ بأن الأبعاد غير متجانسة # لذا الحل np.concatenate((a, np.array([a[0]]))) #array([1, 2, 3, 1])
- 4 اجابة
-
- 1
-

-
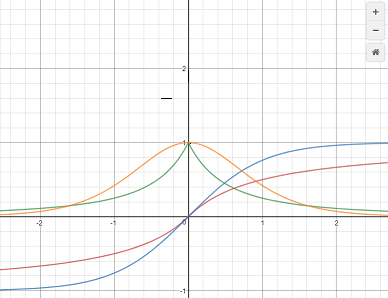
هي دالة تنشيط تستخدم مع الشبكات العصبية وتعطي خرجاً ضمن المجال 1 ل -1. ولها الشكل التالي: softsign(x) = x / (abs(x) + 1). حسناً هذه الدالة مرتبطة ارتباطاً وثيقاً بدالة tanh لذا أنصح أولاً بقراءة مافي الرابط التالي: فهذه الدالة جاءت بغاية تطوير أو تحسين دالة ال tanh بغية منع الخلايا من الوصول لحالة ((التشبع)) بسرعة. أي بمعنى آخر منع الخلايا من الوصول لحالة عدم القدرة على تعلم أي معلومات جديدة. الآن تأمل الرسم البياني التالي، حيث أن الخط الأزرق يمثل دالة ال tanh واللون البرتقالي يمثل مشتقها واللون الأحمر هو دالة ال softsign والأخضر مشتقها. كما تلاحظ فإن دالة التانش تتقارب بشكل سريع من المقارب الأفقي (القيمة y=1 و y=-1) حيث أنها تتقارب منهم بشكل أسي، وهذا مايؤثر سلباً على قيم المشتق حيث أن ميل المماس يصبح أفقياً بسرعة كبيرة مع زيادة قيم ال x وهذا مايعني أن قيم المشتقة تنخفض وهذا مايعني أن عملية التعلم تتباطأ أسياً حتى تنعدم تقريباً في حالة استمرار تزايد قيمة قيم الدخل وهذا مانسميه بحالة (التشبع) أي أن الخلايا لم تعد قاردة على التعلم من البيانات أكثر من ذلك وهذا واضح جداً من الرسم جانباً حيث أن دالة المشتق للتانش تتقارب سريعاً من الصفر. الآن لو نظراً لدالة السوفت فإن أول أمر يمكننا ملاحظته هو أن دالة السوفت كما يشير اسمها هي دالة أنعممم والمقصود هنا أن دالة المشتق لها تتقارب ولكنها لاتنعتدم بسرعة كما في ال tanh وبالتالي منع الخلايا من التشبع. وهي الميزة الوحيدة لها مقارنة بال tanh أما على الجانب الآخر فنجد أن قيم المشتق للتانش أكبر ضمن مجال الدخل من -1 ل 1 وهذا أفضل لعملية التعلم. وفي كيراس يمكننا أن نجدها ضمن الموديول التالي: tf.keras.activations.softsign(x) ولاستخدامها أثناء تدريب نماذجك يمكنك تمريرها للطبقة بإحدى الطرق في المثال التالي: model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='softsign'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.softsign)) أو بالشكل التالي model.add(Dense(64)) model.add(Activation(activations.softsign )) # أو model.add(Activation("softsign ")) """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary()
-
الخطأ في استخدامك ل sparse_categorical_crossentropy في تجميع النموذج بعد أن قمت بتحميله. إن نموذجك الأساسي يستخدم categorical_crossentropy الذي يتعامل مع أهداف "target" مرمزة بترميز One-Hot. وهذا ماتم من خلال التابع np.utils.to_categorical بينما sparse_categorical_crossentropy تتوقع منك أن يكون ترميز الأهداف بالترميز الصحيح Integer Encoding ولهذا السبب يحتج كيراس لاستخدامك sparse_categorical_crossentropy. حيث يتوقع أبعاد (1, ؟) لل y_test، بينما أنت تقدم له أبعاد (10, ؟) لذا يجب أن تستخدم هنا categorical_crossentropy: model.compile( ..., loss='categorical_crossentropy' ) أو: y_test = np.argmax(y_test) وهناك مسألة مشابهة لها تجدها في هذا الرابط: https://academy.hsoub.com/questions/16732-ظهور-الخطأ invalidargumenterror- logits-and-labels-must-have-the-same-first-dimension-في-كيراس-keras/
-
عندما يكون ترميز ال label هو ترميز One-Hot نستخدم CategoricalCrossentropy أو اختصاراً CCE. أما عندما يكون ترميز ال label هو الترميز الصحيح Integer Encoding (في نموذجك لديك 46 فئة وبالتالي كل فئة يتم ربطها بعدد صحيح يمثلها أي 1,2,3,4...etc) نستخدم SparseCategoricalCrossentropy أو اختصاراً SCCE. وعند محاولة تطبيقهم بالعكس (أي استخدام SCCE مع بيانات مرمزة بال One-Hot)يظهر لنا هذا الخطأ. وبشكل عام الدالتين يتبعان لنفس الفكرة والنهج (الانتروبيا المتقطعة) أي كلاهما متطابقان لكن الفرق في طريقة تطبيقهما فالأولى تتعامل مع بيانات بترميز معين والأخرى بترميز آخر (لكن SCCE أفضل من ناحية الكفاءة باستخدام الذاكرة+السرعة). لذا يجب عليك القيام بإحدى الأمرين التاليين: إما أن تستبدل scce ب cce : mymodel.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['CategoricalAccuracy']) أو إذا كنت مصراً على scce يمكنك أن تلغي عملية الترميز One-Hot أي يصبح النموذج: from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=100) # تررميز البيانات import numpy as np def vectorize_sequences(sequences, dimension=100): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) # بناء النموذج from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(64, activation='relu', input_shape=(100,))) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(46, activation='softmax')) # التجميع model.compile(optimizer='rmsprop', loss='SparseCategoricalCrossentropy', metrics=['acc']) # التدريب history = model.fit(x_train, one_hot_train_labels, epochs=10, batch_size=512) model.save("model.h5") يمكنك أيضاً أن تقوم بعكس الترميز (عكس ترميز ال One-Hot أي أن تعيده لشكله الأصلي وهو الترميز بأعداد صحيحية) وبالتالي يصبح بإمكانك أن تستخدام دالة التكلفة scce معه ويمكنك استخدام الدالة np.argmax للقيام بذلك. وفي الروابط التالية توضيح لدالتي التكلفة:
-
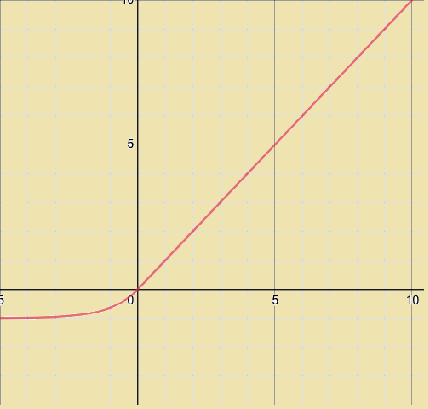
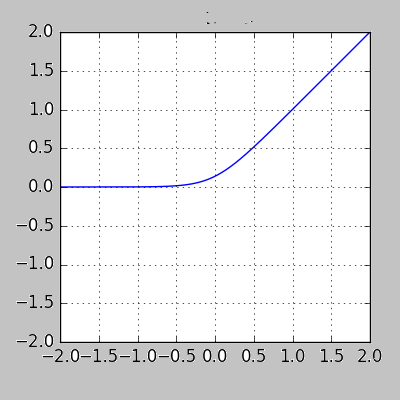
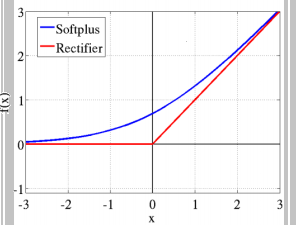
هذه الدالة لها الشكل التالي: Softplus function: f(x) = ln(1+ex) # أو بشكل برمجي أوضح softplus(x) = log(exp(x) + 1) الآن لوعرضنا الرسم البياني لهذا التابع سنجد أنه بالشكل التالي: سنناقش هذه الدالة في حالتين: الأولى على المجال من 0 ل ∞- وهنا نجد أن قيمة الدالة تتناهى لل 0 كلما ابتعدنا عن ال 0 لقيم الدخل، وبالتالي سنجد أنها تسلك نفس سلوك دالة السيني من جهة، ومن جهة أخرى نجد أنها تشبه لحد ما دالة ال ReLU لكنها (أنعم) فدالة ال Relu مباشرة تصبح 0 من أجل القيم السالبة (وهذا مايجعلها تفقد بعض المعلومات-العيب الرئيسي لدالة الريلو-) أما دالة السوفت بلس فتأخذ مسار منحني قبل أن تصبح 0. وهذا مايوضحه الشكل التالي: الحالة الثانية من أجل القيم الموجبة، أي ضمن المجال 0 ل ∞+ نجد أنه هنا يمكن الفرق الجوهري بينها وبين السيني رغم أن بدايتها تشبهه، حيث أننا نجد أن قيم التابع مستمرة باتجاه اللانهاية ولاتتقارب عند القيمة 1 كما في السيني من جهة، ومن جهة أخرى نلاحظ أنها نسخة أنعم من دالة الريلو حيث أن دالة الريلو تأخذ شكل خطي على هذا المجال بينما السوفت تأخذ مسار غير خطي. الآن نذهب للناحية الأهم وهي الاشتقاق وهو مايهمنا في عملية الانتشار الخلفي وتحديث الأوزان. حسناً، هذه الدالة بينها وبين دالة السيني علاقة قوية وهي أن مشتق دالة ال softplus هو دالة السيني. dy/dx = 1 / (1 + e-x) هذا يعني أن قيم مشتقاتها ستكون ملائمة جداً لعملية التعلم، وهي تتفوق على السيني في هذا الأمر (السيني يعاني جداً من تلاشي المشتقات عند القيم الكبيرة للدخل وهذا مايعيق عملية التعلم). وتتفوق على relu من ناحية التعلم من القيم السلبة للدخل فالريلو تعطي قيمة 0 للمشتق من أجل القيم السلبة بينما تعطي سوفتبلس قيمة (حتى ولو أنها صغيرة). لكن relu أفضل منها في القسم الموجب للدخل لأن مشتقها دوماُ يكون 1. بينما السوفت تتدرج من 0 ل 1 حسب قيم الدخل (عملياً قيم z). في كيراس لها الشكل التالي: tf.keras.activations.softplus(x) مثال: import tensorflow as tf a = tf.constant([-20, -1.0, 0.0, 1.0, 20], dtype = tf.float32) b = tf.keras.activations.softplus(a) b.numpy() """ array([2.0611537e-09, 3.1326169e-01, 6.9314718e-01, 1.3132616e+00, 2.0000000e+01], dtype=float32) """ ويمكنك استخدامه في الطبقات الخفية لنموذجك (لاتستخدمه مع طبقة الخرج)، انظر للمثال التالي الذي سأوضح فيه كيفية استخدامه بكل الطرق: from keras.datasets import imdb from keras import preprocessing max_features = 10000 maxlen = 20 (x_train, y_train), (x_test, y_test) = imdb.load_data( num_words=max_features) x_train = preprocessing.sequence.pad_sequences(x_train, maxlen=maxlen) # هنا حددنا طول الكلمات ب 20 x_test = preprocessing.sequence.pad_sequences(x_test, maxlen=maxlen) # بناء نموذجك from keras.models import Sequential from keras.layers import Flatten, Dense,Embedding model = Sequential() model.add(Embedding(10000, 8, input_length=maxlen)) model.add(Flatten()) model.add(Dense(64, activation='softplus'))# بهذه الطريقة """ أو from tensorflow.keras import activations model.add(Dense(64, activation=activations.softplus)) أو بالشكل التالي model.add(Dense(64)) model.add(Activation(activations.softplus)) # أو model.add(Activation("softplus")) """ model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc']) model.summary() # تدريبه history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2)
-
يمكنك القيام بذلك من خلال الدالة reshape هذه الدالة تمكنك من تعديل أبعاد المصفوفة بالشكل الذي تريده، والشرط الوحيد هو أن كون عدد العناصر في المصفوفة الجديدة التي تريد إعادة تشكيلها = عدد العناصر في المصفوفة الأصلية. أي إذا كانت المصفوفة الأصلية مصفوفة أحادية البعد ب 12 عنصر وأردنا تحويلها لمصفوفة ثنائية ببعدين وبالتالي يجب أن يكون ناتج جداء البعد الأول بالثاني =12 وبالتالي يمكن أن نستنتج أن أبعاد المصفوفة الناتجة إحدى الخيارات التالية: a=np.arange(12) a.reshape(3,4) """ array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) """ a.reshape(4,3) """ array([[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11]]) """ a.reshape(6,2) """ array([[ 0, 1], [ 2, 3], [ 4, 5], [ 6, 7], [ 8, 9], [10, 11]]) """ a.reshape(2,6) # 12!=4*4 هنا سيظهر خطأ كما قلنا لأن a.reshape(4,4) # ValueError: cannot reshape array of size 12 into shape (4,4) كما أننا يمكننا أن نمرر له بعد واحد والبعد الآخر نضع مكانه -1 و هو سيستنتجه تلقائياً وفقاُ لمعادلة الجداء: a=np.arange(12) a.reshape(-1,4) # سيستنتج أنه3 """ array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) """ a.reshape(-1,3)#4 سيستنتج أنه """ array([[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11]]) """ # وهكذا....
-
هذا صحيح يجب أن تتم العملية من دون مشاكل لأن شرط ضرب المصفوفتين محقق، لكن أنت تستخدم المعامل الخطأ لضرب المصفوفتين.فالمعامل * يستخدم لتطبيق عملية الضرب عنصر بعنصر أي eliment-wise أي يقوم بضرب العناصر المتقابلة من المصفوفتين وبالتالي يجب أن تكون المصفوفتين بأبعاد متطاااابقة بالطول والعرض. أما إذا أردت تنفيذ عملية الضرب العادي للمصفوفات فهنا يجب أن تستخدم التابع dot (ولاتخلط بينه وبين ال . فال . ليس لها علاقة بالجداء وإنما هي خاصة بال attribute واستخدامها هنا سيعطي خطأ): import numpy as np a = np.array([[2, 1],[2,4]]) b = np.array([[2, 1],[2,4]]) # ضرب عاددي print(a.dot(b)) """ [[ 6 6] [12 18]] """ # eliment-wise print(a * b) """ [[ 4 1] [ 4 16]] """ لكن مهلاً دعني أوضح معنى الخطأ هو يقول لك أنه فشل في تطبيق عملية تسمى "brodcast" وهي عملية يطبقها بايثون عندما تكون العملية المطلوبة غير قابلة للتطبيق (في حالتك لديك مصفوفتين بأبعاد مختلفة وتحاول تطبيق عملية ضرب عنصر بعنصر وهذا غير ممكن، لكن بايثون لاتستسلم بهذه السهولة، لذا يحاول جعل المصفوفة الصغيرة بنفس أبعاد الكبيرة لكي تتم العملية لكنه أيضاً يفشل لماذا؟ سأشرح هذا بعد قليل). حسناً ..بايثون تدعم مانسميه ال broadcast وهو مصطلح يشير إلى كيفية تعامل numpy مع المصفوفات ذات الأبعاد المختلفة أثناء العمليات الحسابية التي لها قيود معينة، يتم تطبيق broadcast للمصفوفة الأصغر لتتطابق مع المصفوفة الأكبر بحيث يكون لها شكل متوافق لتنفيذ العملية. وهذا أمر مفيد جداً في علوم تعلم الآلة. وبشكل أوضح أو أكثر دقة عندما تحاول تطبيق عملية (eliment-wise) ضرب أو طرح أو تطبيق أي عملية رياضية على مصفوفتين غير متوافقتين بالأبعاد فإن بايثون سيحاول جعل المصفوفتين متوافقتين لكي تتم العملية، حيث يقوم بنسخ وتكرار وتوسيع للمصفوفة الصغيرة بحيث تحقق شرط تطبيق العملية المطلوبة، وبشكل أدق ركز معي: لو كان لديك مصفوفة ابعادها (m,n) وقمت بجمعها او طرحها او ضربها او قسمتها على مصفوفة من الحجم (1 عمود و n سطر) سيتم نسخ المصفوفة الثانية m مرة ليصبح حجمها مثل حجم المصفوفة الأولى. وبشكل مشابه لو كان لديك مصفوفة بحجم m سطر و 1 عمود، سيتم نسخ هذه المصفوفة n مرة لتصبح بحجم الأولى أي (m,n) ومن ثم تطبيق العملية المرادة. ، مثال: import numpy as np a1 = np.array([2, 4, 3]) a1.shape # (3,) a2 = np.array([50, 2, 10]) a2.shape # (3,) # هنا مصفوفتين متوافقتين بالحجم لكن لايمكن ضربهما ضرب مصفوفات عادي لكن هنا يتم ضربهما عنصر بعنصر c = a1 * a2 print (c) #[350 4 180] مثال آخر: import numpy as np a1 = np.array([2, 4, 3]) a1.shape # (3,) a2 = 3 #brodcast هنا غير متطابقين ولا يتحقق شرط الجمع لكن يتم تنفيذ عملية c = a1 + a2 print(c) #[5 7 6] مثال: import numpy as np a1 = np.array([[1, 2, 3], [10, 2, 30]]) a2 = 4 C = a1 + a2 print(C) """ [[ 5 6 7] [14 6 34]] """ لكن لل brodcast شروط وهي أن المصفوفتين يجب أن تتطابق إحدى أبعادهما وإلا يفشل وهذا ماحدث معك. a = np.random.randn(97,2) b = np.random.randn(2,1) a*b #ValueError: operands could not be broadcast together with shapes (97,2) (2,1)
- 3 اجابة
-
- 1
-

-
كما نعلم فأن مجال الثقة هو مجال عددي يُتوقع أن يحتوي على القيمة الحقيقية لمَعلَمة (كمية عددية تميّز و"تلخص" التوزع الاحتمالي لمجموعة من الأحداث المتشابهة) إحصائية يراد معرفتها لمجموعة من العناصر أو الأحداث المتشابهة (تسمى في عالم الإحصاء مجتمع إحصائي) التي تكون (بجميع عناصرها) موضوعا لدراسة علمية ما.في أغلب الأبحاث أن يتم استخدام مجالات ثقة بمستوى ثقة قدره 95% ولكن يمكن أن يتم أيضا حسابها بمستويات ثقة أخرى مثل 99% و90%. في بايثون يمكنك استخدام scipy.stats.t.interval للحصول على مجال الثقة لعينة إحصائية ما. في بايثون يمكنك حسابه كالتالي: import scipy import scipy.stats as s import numpy as np sample=np.array([1,2,3,4,5,6]) confidence_level = 0.95 degrees_freedom = sample.size - 1 mean = np.mean(sample) standard_error = scipy.stats.sem(sample) confidenceinterval = s.t.interval(confidence_level, degrees_freedom, mean, standard_error) confidenceinterval # (1.5366856922723917, 5.463314307727608) استخدم numpy.ndarray.size - 1 مع numpy.array كمصفوفة من بيانات العينة للعثور على درجة الحرية. ثم استدعي numpy.mean(arr) لحساب المتوسط الحسابي لبيانات العينة arr، ثم استدعي scipy.stats.sem(arr) لحساب الخطأ المعياري لها "standard error" (طريقة قياس أو تقدير الانحراف المعياري) ثم استدعي scipy.stats.t.interval(confidence_level, degrees_freedom, mean, std) لحساب مجال الثقة. يمكنك أيضاً حسابها بالشكل التالي من خلال استخدام الدالة NormalDist : from statistics import NormalDist import scipy import numpy as np sample=np.array([1,2,3,4,5,6]) def confidenceinterval(s, confidence=0.95): #NormalDist.stdev& NormalDist.mean ترجع لنا كائن يحتوي معلومات أهمها المتوسط والانحراف المعياري من خلال استدعاء الواصفتين dist = NormalDist.from_samples(s) z = NormalDist().inv_cdf((1 + confidence) / 2.) h = dist.stdev * z / ((len(s) - 1) ** .5) return dist.mean - h, dist.mean + h
- 2 اجابة
-
- 1
-

-
https://academy.hsoub.com/questions/16284-تحويل-tensor-إلى-مصفوفة-numpy-في-tensorflow؟/#comment-47170 هناك سؤال مشابه له هنا. فقط استدعي ()tensor.numpy على ال Tensor object # tensorflow_version 2.x # مثال1 import tensorflow as tf t = tf.constant([[1, 2], [4, 8]]) a = t.numpy() print(a) print(type(a)) """ [[1 2] [4 8]] <class 'numpy.ndarray'> """ # مثال 2 import tensorflow as tf a = tf.constant([[1, 2], [3, 4]]) b = tf.add(a, 1) a.numpy() # array([[1, 2], # [3, 4]], dtype=int32) b.numpy() # array([[2, 3], # [4, 5]], dtype=int32) tf.multiply(a, b).numpy() # array([[ 2, 6], # [12, 20]], dtype=int32) إذا كانت النسخة هي TensorFlow version 1.x استخدم: tensor.eval(session=tf.compat.v1.Session()) مثال: # tensorflow_version 1.x import tensorflow as tf t = tf.constant([[1, 2], [4, 8]]) a = t.eval(session=tf.compat.v1.Session()) print(a) print(type(a)) أيضاً يجب أن تعلم أنه بمجرد استخدامك لأي عملية من عمليات نمباي على ال tensor سوف تتحول تلقائياً إلى numpy array، في الكود التالي مثلاً ، نقوم أولاً بإنشاء Tensor وتخزينه في متغير t عن طريق إنشاء ثابت Tensor ثم استخدام تابع الضرب في TensorFlow والناتج هو نوع بيانات Tensor أيضاً . بعد ذلك ، نقوم بإجراء عملية np.add () على Tensor التي تم الحصول عليها من خلال العملية السابقة. وبالتالي ، تكون النتيجة عبارة عن NumPy ndarray حيث تم إجراء التحويل تلقائيًا بواسطة NumPy. import numpy as np import tensorflow as tf #tensor إنشاء كائن t = tf.constant([[1, 2], [4, 8]]) t = tf.multiply(t, 2) print(t) # تطبيق عملية من نمباي a = np.add(t, 1) print(a)
- 2 اجابة
-
- 1
-

-
يجب أن تقوم بعمل Compile للنموذج (ترجمة له) بحيث تحدد له معلومات مثل نوع دالة التكلفة والمعيار الذي تريد تطبيقه لحساب الدقة أثناء التدريب. Model.compile( optimizer="rmsprop", # المحسن الذي تريد تطبيقه loss=None, # دالة التكلفة التي تريد تطبيقها metrics=None, # معيار حساب الكفاءة ) أي يصبح نموذجك: from keras.datasets import reuters (train_data, train_labels), (test_data, test_labels) = reuters.load_data( num_words=10000) # تررميز البيانات import numpy as np def vectorize_sequences(sequences, dimension=10000): results = np.zeros((len(sequences), dimension)) for i, sequence in enumerate(sequences): results[i, sequence] = 1. return results x_train = vectorize_sequences(train_data) x_test = vectorize_sequences(test_data) from keras.utils.np_utils import to_categorical one_hot_train_labels = to_categorical(train_labels) one_hot_test_labels = to_categorical(test_labels) x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = one_hot_train_labels[:1000] partial_y_train = one_hot_train_labels[1000:] # بناء النموذج from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(64, activation='relu', input_shape=(10000,))) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(46, activation='softmax')) # التجميع model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['acc']) # التدريب history = model.fit(partial_x_train, partial_y_train, epochs=6, batch_size=512, validation_data=(x_val, y_val)) حيث نقوم بعملية التجميع أو الترجمة compile قبل عملية التدريب. لكي يفهم النموذج ماهي دالة الخسارة وماهو معيار الدقة و ال optimizer الذي سيستخدمه. وفي حالتك فإن مهمتك هي مهمة تصنيف متعدد وبالتالي يجب أن تستخدم دالة تكلفة تناسب مهمتك، وبما أن بياناتك مرمزة بترميز onehot وبالتالي يجب أن تستخدم دالة التكلفة categorical_crossentropy أما المعيار فيمكنك تحديد accuracy أو معيار آخر مثل categorical_crossentropy .أما بالنسبة لل optimizer فتمنحك كيراس كل الخيارات وأبرزها adam و rmsprop.
-
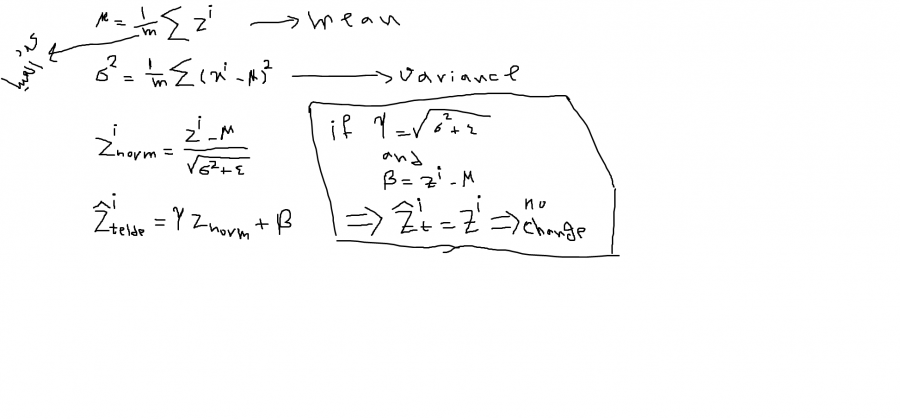
هي القيام بعملية تقييس "Scaling" للبيانات ضمن الطبقات الخفية للشبكات العصبونية. اعتدنا دوماً أن نقوم بعملية تقييس لبيانات الدخل بحيث نجعلها تنتمي إلى "Range" معين. مثلاً في الصور كنا نقسم كل البكسلات على 255 بحيث تصبح قيم البكسلات بين ال0 و1. وهذا ماكان يؤدي إلى تحسين أداء النموذج من ناحية السرعة والدقة والتعميم. لكن ماذا عن الطبقات الخفية. يمكننا القيام بعملية تقييس للبيانات في الطبقات الخفية (قيم ال z أو قيم ال acttivations لكن غالباً مايطبق على z وهذا أفضل عموماً). وهذا ماسيجعل النموذج يتدرب بشكل أسرع إضافة إلى جعله قادراً على التعميم بشكل أكبر . وتمنحه القدرة على حل مشكلة ال Convariate shift (أي إذا قمنا بالربط بين المدخلات x والمخرجات y أي دربنا نموذج للقيام بذلك ) فإن اختلاف توزيع x (الشكل الذي تتوزع به البيانات أي بمعنى آخر مجالات القيم) سيؤدي إلى اختلافات كبيرة في قيم z (أو قيم ال activations) في الطبقات الخفية، وهذ ماسينتج عنه نتائج مختلفة جداً تماماً كمبدأ (أثر الفراشة حيث تؤدي التغيرات البسيطة في البداية إلى أحداث كبيرة لاحقاً). على سبيل المثال إذا كان نموذجك مدرباً على صور قطط سوداء وبيضاء فقط (توزيع بيانات محدد) وقمت باختباره على قطط ملونة (توزيع مختلف) سيؤدي إلى ظهور نتائج غير صحيحة.. لن أدخل بتفاصيل أكثر.. وتظهر هذه المشكلة عموماً في الشبكات العصبية الكبيرة مثلاً مثل شبكة AlexNet. لذا سأقوم بعرض مثال عليها وكيف نطبق ال Batch Normlaization عليها في كيراس، بعد قليل. هذه التقنية تعتمد على حساب متوسط مجموع قيم z للطبقة المطبق عليها أي حساب ال mean. ثم حساب ال variance (متوسط مجموع مربعات الفروق بين قيم z وال mean). ثم حساب مايسمى znorm وتساوي (قيمة z مطروحاً منها قيمة ال mean) والناتج مقسوم على جذر ال variance مضافاً له قيمة متناهية في الصغر تسمى epsilon لتجنب حالة انعدام المقام وبالتالي القسمة على صفر. ثم بعد ذلك حساب قيمة مايسمى ztelde وتساوي قيمة znorm مضروبة بغاما ومضاف لها قيمة بيتا. وهي التي تمثل القيمة النهائية (أي أن ztelde هي القيمة التي سنستبدل بها قيمة z الأصلية). إليك الشكل الرياضي للفكرة، حيث m عدد العينات: لاحظ أنه كلما ابتعدت قيم غاما وبيتا عن القيم المشار لها في الأعلى يزاد ال normlaize. وكلما اقتربت منها يقل التأثير. الآن قد يتبادر لأذهاننا كيفية اختيار قيم غاما وبيتا والإجابة هي أننا نختارهما بقيم عشوائية لأن الشبكة العصبية تعاملهما معاملة الأوزان وبالتالي تقوم بتعديل قيمهما من خلال خوارزمية الانتشار الخلفي كما تراه مناسباً. أي يتم اعتبارهما learnable parameters. وأي خوارزمية تحسين (adam أو momentum أو rmsprop أو غيرهم..) تقوم بتحديث قيمهم بنفس الطريقة التي تحدث فيها قيم الأوزان. وتجدر الملاحظة إلى أنه لايجب علينا استخدام هذه التقنية مع طبقة الدخل لأن أثرها سيكون سلبي (لأنها تجعل قيم ال mean=0 وال variance=1 ). وأيضا عند تطبيقه لايوجد داع لاستخدام قيم لل bias لأن beta ستفي بالغرض. كما تجدر الملاحظة إلى أن هذه التقنية تضيف نوعا ً من التنعيم للنموذج. لأنه مع كل mini batch يتم حساب mean و variance مختلفين وهذا يضيف نوعاً من التنعيم للنموذج بشكل مشابه لل dropout. الآن يجب أن تعلم أنه عند تطبيق هذه التقنية فإنه يتم حساب ال mean و variance لكل minibatch بشكل منفصل. أي أن كل ميني باتش سيتبع توزيعاً مختلفاً قليلاً عن الآخر تبعاً لاختلافهما. وهنا يظهر ليدنا السؤال التالي، كيف سيتم اختبار قيمهما في وقت الاختبار؟ تكون قيم ال mean و ال variance المستخدمة في وقت الاختبار هي القيمة النهائية المقدرة لهم خلال التدريب اعتماداً على فكرة المتوسطات الأسية الموزونة EWA ويكون ال Average عبر كل ال minibatches وهذه الطريقة تسمى running aveeage. فقيم ال mean وال variance تكون مختلفة من mini batch إلى آخر في وقت التدريب وبالتالي نحتاج لقيمة محددة نستخدمها خلال الاختبار لأنه في وقت الاختبار قد لايكون لديك سوى عينة واحدة فقط وبالتالي حساب ال mean وال variance ليس له معنى .. لذا يجب تحديد قيمة لهم مسبقاً خلال مرحلة التدريب.ليكون عملك فعالاً وصحيحاً. بشكل عام التفاصيل الدقيقة الأخرى لاتهمك كثيراً عند استخدام إطارات العمل فكل هذه التفاصيل تكون تلقائية لكن يهمنا فهم الفكرة العامة. لكي نعرف ماذا نقوم به (لكي لاتكون ببغاءاً في هذا المجال وفاقداً للإبداع في استخدام اطارات العمل). الآن لنرى شكلها العام: tf.keras.layers.BatchNormalization( axis=-1, momentum=0.99, epsilon=0.001, center=True, scale=True, beta_initializer="zeros", gamma_initializer="ones", moving_mean_initializer="zeros", moving_variance_initializer="ones", beta_regularizer=None, gamma_regularizer=None, beta_constraint=None, gamma_constraint=None, ) في كيراس لها الشكل الجميل السابق حيث تضاف للنموذج كطبقة. وطبعاً كلها ستكون واضحة لك الآن بعد الشرح السابق. الوسيط epsilon تحدثنا عنه (منع القسمة على صفر)، الوسيطين beta_initializer و gamma_initializer يحددان الطريقة التي سيتم تهيئة قيمهما فيها (أيضاً تحدثنا عنهم) لكن لاحظ أنه إياك أن تقوم بتهيئة غاما بصفر فالشبكة ستتعطل. الوسيطين moving_mean_initializer و moving_variance_initializer و momentum هم الوسطاء الخاصين بال EWA فأول وسيطين هما قيم التهيئة والمومنتوم لها، حيث يتم تحديث قيم الmean وال variance من خلال المعادلات: moving_mean = moving_mean * momentum + mean(batch) * (1 - momentum) moving_var = moving_var * momentum + var(batch) * (1 - momentum) أما بالنسبة للوسيط center ففي حالة وضعه على False سيقوم بإلغاء ال beta (هنا لابد من إضافة ال bias للأوزان). أما ال scale ففي حال وضع False سيتم إلغاء استخدام غاما. أما gamma_regularizer و beta_regularizer فهما لتحديد فيما إذا أردت تطبيق تنعيم عليهم أم لا.الوسيط beta_constraint و gamma_constraint هما قيد اختياري لوزن جاما أو بيتا. وأخيراً axis وهي المحور الذي سيتم تطبيق ال normlaize عليه (عادةً محور ال Features). الآن يجب أن نعلم أنه خلال التدريب يتم تطبيق ال normlaize بناءان على قيم ال mean و ال var للباتش الحالي. أي: gamma * (batch - mean(batch)) / sqrt(var(batch) + epsilon) + beta أما عند الاختبار يتم تطبيقه بناءان على قيم ال mean وال var الذي تم حسابهما خلال مرحلة التدريب اعتماداً على الفكرة التي شرحتها. أي: gamma * (batch - self.moving_mean) / sqrt(self.moving_var + epsilon) + beta. أيضاً هناك وسيط آخر لم يذكر في توثيق كيراس لكن يمكن تمريره وهو training ويأخذ إما True أو False ففي حال وضعه على True فهذا يعني أنك الآن في وضع التدريب وبالتالي قيم ال mean وال var تحسب على أساس الباتش الحالي، أما وضعه على false فيعني أنك تحسب على أساس المتوسطات الأسية سالفة الذكر. (افتراضياً يقوم كيراس بضبط هذه الأمور بالشكل الصحيح لذا ربما بم توضع فهو يفهم من تلقاء نفسه أن استدعاء fit يعني أننا في طور التدريب وبالتالي يكون الوسيط مضبوط على true أما عند استخدام evaluate أو pridect فهو يفهم أنك في طور التدريب أي يجعله false). وفي كيراس يطبق على قيم ال Activation. الآن سنضع المثال حيث يتم إضافتها في النموذج كطبقة، مثلاً كان لدينا طبقة Dense وبالتالي إذا وضعنا بعدها طبقة batchnorm فهذا يعني أنه سيتم تطبيق تقنية ال batcjhnorm عليها.المثال التالي يمثل شبكة ALEXNET المشهورة: #Importing library import keras from keras.models import Sequential from keras.layers import Dense, Activation, Dropout, Flatten, Conv2D, MaxPooling2D from keras.layers.normalization import BatchNormalization import numpy as np np.random.seed(1000) #Instantiation AlexNet = Sequential() #1st Convolutional Layer AlexNet.add(Conv2D(filters=96, input_shape=(100,100,3), kernel_size=(11,11), strides=(4,4), padding='same')) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) AlexNet.add(MaxPooling2D(pool_size=(2,2), strides=(2,2), padding='same')) #2nd Convolutional Layer AlexNet.add(Conv2D(filters=256, kernel_size=(5, 5), strides=(1,1), padding='same')) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) AlexNet.add(MaxPooling2D(pool_size=(2,2), strides=(2,2), padding='same')) #3rd Convolutional Layer AlexNet.add(Conv2D(filters=384, kernel_size=(3,3), strides=(1,1), padding='same')) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) #4th Convolutional Layer AlexNet.add(Conv2D(filters=384, kernel_size=(3,3), strides=(1,1), padding='same')) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) #5th Convolutional Layer AlexNet.add(Conv2D(filters=256, kernel_size=(3,3), strides=(1,1), padding='same')) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) AlexNet.add(MaxPooling2D(pool_size=(2,2), strides=(2,2), padding='same')) #Passing it to a Fully Connected layer AlexNet.add(Flatten()) # 1st Fully Connected Layer AlexNet.add(Dense(2000, input_shape=(32,32,3,))) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) # Add Dropout to prevent overfitting AlexNet.add(Dropout(0.4)) #3rd Fully Connected Layer AlexNet.add(Dense(512)) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('relu')) #Add Dropout AlexNet.add(Dropout(0.4)) #Output Layer AlexNet.add(Dense(1)) AlexNet.add(BatchNormalization()) # هنا AlexNet.add(Activation('sigmoid')) #Model Summary AlexNet.summary() AlexNet.compile(optimizer="adam",loss="binary_crossentropy",metrics=["accuracy"]) #Ali Ahmed is where there is machine learning