كيفية إيجاد الزاوية بين شعاعين في فضاء ثنائي الأبعاد 2D

ناقشنا في المقال السابق بعض استخدامات الجداء النقطي والتي هي:

حساب طول الشعاع: حيث يكون الجداء النقطي للشعاع مع نفسه = الطول².
اكتشاف تعامد شعاعين: حيث يكون الجداء النقطي لشعاعين متعامدين = 0.

تساوي الزاوية بين الشعاع ونفسه 0 درجة في الحالة الأولى، وتساوي الزاوية بين الشعاعين 90 درجة في الحالة الثانية، وبالتالي يمكن القول أن الزاوية بين الشعاعين لها علاقة بالجداء النقطي، إذ قد يكون حاصل الجداء النقطي كبيرًا عندما تكون الزاوية بين الشعاعين قريبة من الصفر وصغيرًا عندما تكون الزاوية بينهما قريبة من الزاوية القائمة.

سنناقش في هذا المقال المواضيع التالية:

الخاصيتان المتعلقتان بالجداء النقطي للأشعة.
صيغة لحساب الزاوية بين شعاعي وحدة Unit Vectors.
عدد الأشعة التي تبعد عن شعاع معين بالمقدار الزاوي نفسه.
معنى جيب التمام السالب للزاوية بين شعاعين.
كيفية العثور على الزاوية بين الأشعة التي ليست أشعة وحدة.

تأثير طول الأشعة على الجداء النقطي

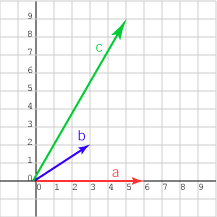
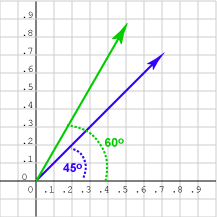
لنفكّر حاليًا في الأشعة في فضاء ثنائي الأبعاد مثل الشعاع a في الرسم البياني السابق، حيث يُحتمَل أن يكون جداؤه النقطي مع الشعاع c الذي له منحى Orientation مقداره 60 درجة أكبر من جدائه النقطي مع الشعاع b الذي له منحى مقداره 30 درجة، لأن الشعاع c أطول بكثير من الشعاع b، ولنتأكد الآن من ذلك الآن. ولتكن لدينا الأشعة التالية:

a = (6, 0)^T

b = (3, 2)^T

c = (5, 9)^T

ويكون الجداء النقطي لها هو:

a · b = 18.0

a · c = 30.00

توجد خاصيتان متعلقتان بحاصل جداء الأشعة النقطي كما ذكرنا سابقًا وهما:

الزاوية بين أشعة الإدخال.
طول أشعة الإدخال.

ولكننا نرغب الآن في إبقاء تأثير الزاوية فقط من خلال إزالة تأثير الطول بطريقة أو بأخرى، ويمكننا إزالة تأثير الطول باستخدام توحيد Normalize الأشعة، أي إنشاء أشعة الوحدة Unit Vectors في الاتجاه نفسه كما سنوضح في الفقرة التالية.

توحيد الأشعة

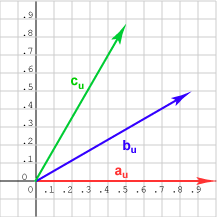
يوضّح الرسم البياني السابق كل شعاع بعد توحيده، أي إنشاء شعاع وحدة باتجاه الشعاع الأصلي نفسه.

ملاحظة: تذكّر أن الحرف u المنخفض يشير إلى شعاع الوحدة: ‎b_u‎.

إلغاء تأثير الطول على جداء الأشعة النقطي

لنتأكد الآن من الجداء النقطي الأكبر من بين الجداءين ‎a_u · b_u‎ و ‎a_u · c_u‎ بعد أن وحّدنا الأشعة لإلغاء تأثير الطول على الجداء النقطي.

بما أن: u · v = | u | | v | cos θ، وجميع الأشعة طولها يساوي 1.0، فإن الجداء النقطي ‎u · v = cos θ، وبالتالي فإن الجداء النقطي ‎a_u · b_u‎ يساوي جيب تمام الزاوية بين الشعاعين ‎a_u‎ و ‎b_u‎، والذي يمكن قراءته من الرسم البياني على أنه 0.866، بينما يساوي الجداء النقطي ‎a_u · c_u‎ جيب تمام الزاوية بين ‎a_u‎ و ‎c_u‎، والذي يمكن قراءته من الرسم البياني على أنه 0.500.

منحى الشعاع ‎b_u‎ أقرب إلى الشعاع ‎a_u‎، لذلك يكون ‎a_u · b_u‎ هو الأكبر حيث:

a_u = (1, 0): شعاع الوحدة عند الزاوية صفر درجة

b_u = (0.866, 0.5): شعاع الوحدة عند الزاوية 30 درجة

c_u = (0.5, 0.866): شعاع الوحدة عند الزاوية 60 درجة

تذكر أن: cos 30 = 0.866 و sin 30 = 0.5 و cos 60 = 0.5 و sin 60 = 0.866.

وبالتالي فإن الجداء النقطي هو:

a_u · b_u = 0.866

a_u · c_u = 0.500

لذا يمكن إزالة تأثير الطول باستخدام أشعة طولها 1، ويكون حاصل الجداء النقطي أكبر عندما تفصل زاوية صغيرة بين الأشعة، وإذا كانت الأشعة في اتجاهات متعاكسة مثل ‎(1, 0)^T‎ و ‎(-1, 0)^T‎، فسيكون مقدار الجداء النقطي سالبًا.

مجال قيمة الجداء النقطي لشعاعي وحدة

سنوضّح فيما يلي عينة لشعاع الوحدة ‎b_u‎ وحاصل الجداء النقطي له مع الشعاع ‎a_u = (1.0, 0)^T‎ لزوايا مختلفة:

الزاوية	الشعاع b	النتيجة	صورة توضيحية
الزاوية 000 درجة	‎(1.000, 0.000)^T‎	تساوي 1.000
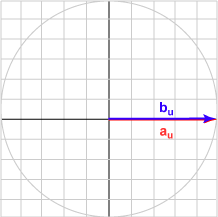
الزاوية 015 درجة	‎(0.966, 0.259)^T‎	تساوي 0.966
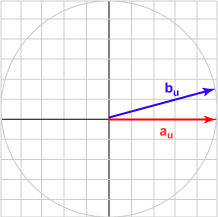
الزاوية 030 درجة	‎(0.866, 0.500)^T‎	تساوي 0.866
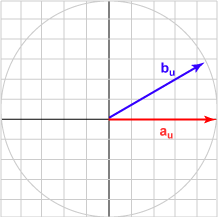
الزاوية 045 درجة	‎(0.707, 0.707)^T‎	تساوي 0.707
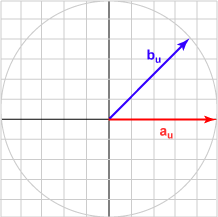
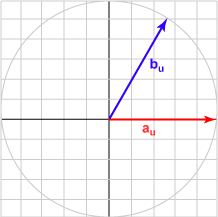
الزاوية 060 درجة	‎(0.500, 0.866)^T‎	تساوي 0.500
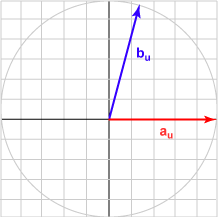
الزاوية 075 درجة	‎(0.259, 0.966)^T‎	تساوي 0.259
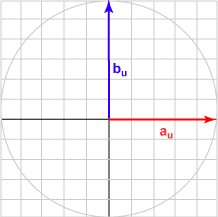
الزاوية 090 درجة	‎(0.000, 1.000)^T‎	تساوي 0.000
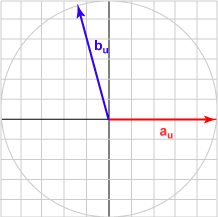
الزاوية 105 درجة	‎(-0.259, 0.966)^T‎	تساوي ‎-0.259 ‫
الزاوية 120 درجة	‎(-0.500, 0.866)^T‎	تساوي ‎-0.500	‫
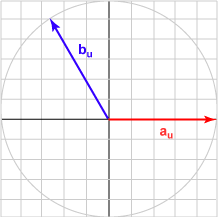
الزاوية 135 درجة	‎(-0.707, 0.707)^T‎	تساوي ‎-0.707	‫
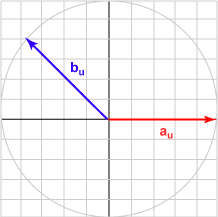
الزاوية 150 درجة	‎(-0.866, 0.500)^T‎	تساوي ‎-0.866	‫
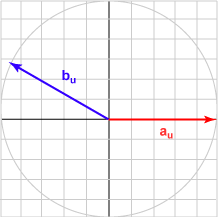
الزاوية 165 درجة	‎(-0.966, 0.259)^T‎	تساوي ‎-0.966	‫
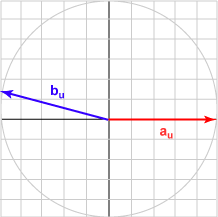
الزاوية 180 درجة	‎(-1.000, 0.000)^T‎	تساوي ‎-1.000	‫

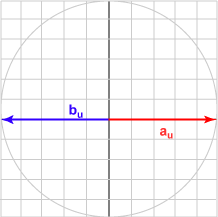
‎b_u‎ هو شعاع الوحدة الذي تمثله المصفوفة ‎(cos θ, sin θ )^T‎ في كل حالة من الحالات.

إذًا مجال قيم حاصل الجداء النقطي لشعاعي الوحدة ‎a_u · b_u‎ هو ‎-1.0 … 1.0.

صيغة حساب الزاوية بين شعاعين

مجال قيم حاصل الجداء النقطي لشعاعي الوحدة ‎a_u · b_u‎ هو ‎-1.0 … 1.0، لأن كل جداء نقطي في الفقرة السابقة هو:

‎(1, 0)^T · ( cos θ, sin θ)^T = cos θ

وهذا صحيح، فعندما يكون ‎a_u‎ شعاع وحدة فإنه سيؤشر إلى أيّ اتجاه، وبالتالي يمكن حساب الزاوية بين شعاعي الوحدة كما يلي:

a_u · b_u = cos θ‎

حيث θ هي الزاوية بين الشعاعين، وتتضمن هذه الصيغة تلقائيًا حقيقة أن الجداء النقطي للأشعة المتعامدة هو صفر، لأن جيب تمام cos الزاوية 90 يساوي الصفر.

أوجد جيب تمام الزاوية بين شعاعي الوحدة اللذين تمثلهما المصفوفتان ‎(0.7071, 0.7071)^T‎ و ‎(0.5, 0.866)^T‎:

cos θ = (0.7071, 0.7071)^T · (0.5, 0.866)^T = 0.7071 · 0.5 + 0.7071 · 0.866 = 0.9659‎

تدريب عملي

تدريب 1:

يوضّح الرسم البياني السابق شعاعين هما: الشعاع الأول ‎(0.7071, 0.7071)^T‎ وهو شعاع وحدة عند الزاوية 45 درجة، والشعاع الثاني ‎(0.5, 0.866)^T‎ وهو شعاع وحدة عند الزاوية 60 درجة، وبالتالي يجب أن يكون حاصل الجداء النقطي لهما هو جيب تمام الزاوية 15. لنوضّح ذلك باستخدام الرموز كما يلي:

الشعاع الأول هو ‎(cos 45, sin 45)^T‎.
الشعاع الثاني هو ‎(cos 60, sin 60)^T‎.
حاصل الجداء النقطي لهما هو:

cos 45 cos 60 + sin 45 sin 60

‎= cos 45 cos(45 + 15) + sin 45 sin(45+15)‎

‎= cos 45 (cos 45 cos 15 - sin 45 sin 15) + sin 45 (cos 45 sin 15 + cos 15 sin45)‎

‎= cos 45 cos 45 cos 15 - cos 45 sin 45 sin 15 + sin 45 cos 45 sin 15 + sin 45 cos 15 sin 45

‎= cos² 45 cos 15 + sin²45 cos 15

‎= (cos²45 + sin²45)cos15

‎= cos 15

استخدامنا في الخطوة رقم 5 القاعدتين التاليتين:

cos(x+y) = cos(x) cos(y) - sin(x) sin(y)‎

sin(x+y) = sin(x) cos(y) + cos(x) sin(y)‎

واستخدامنا في الخطوة رقم 9 القاعدة التالية:

sin²x + cos²x = 1‎

أوجد جيب تمام Cosine الزاوية بين شعاعي الوحدة المُمثَّلان بالمصفوفتين ‎‎q_u = (0.0, 1)^T‎ و ‎r_u = (0.5, 0.866)^T‎:

q_u · r_u = cos θ = 0.866‎

وبالتالي: θ =‫ arc cos 0.866 ‫= 30 درجة.

تدريب 2:

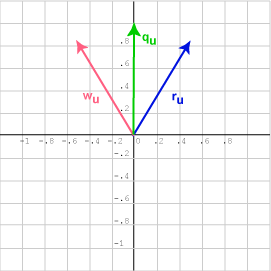
يظهِر الشكل التالي الشعاعان ‎q_u‎ و ‎r_u‎ والزاوية بينهما:

تذكّر أن:

q_u · r_u = r_u · q_u‎

يجب أن تكون الزاوية بين الشعاعين 180 درجة أو أقل (حسب التعريف)، ولا يهم ترتيب الأشعة في الجداء النقطي.

ملاحظة: من المفيد في بعض الأحيان رسم صورة للتأكد من أن إجابتك منطقية خاصةً عندما تؤشر الأشعة إلى أرباع مختلفة.

أوجد جيب تمام الزاوية بين شعاعي الوحدة المُمثَّلان بالمصفوفتين ‎q_u = (0.0, 1)^T‎ و ‎w_u = (-0.5, 0.866)^T‎:

cos x =‫ 0.866، إذًا يجب أن تكون x =‫ arc cos 0.866 =‫ 30 درجة.

لاحظ أن كلا الشعاعين ‎r_u‎ و ‎w_u‎ يعطيان الإجابة cos 30 عند تطبيق الجداء النقطي عليهما مع الشعاع ‎q_u‎، بالرغم من أنهما يقعان على جانبي هذا الشعاع.

يوجد شعاعا وحدة يبعدان بمقدار 30 درجة عن الشعاع المعطَى في الفضاء ثنائي الأبعاد، وسيعطي كلاهما النتيجة نفسها للجداء النقطي مع الشعاع المُعطى، لذا يجب أن تكون حذرًا في رسم الأشعة في الحالات الغامضة.

الزوايا بين شعاعين التي تكون أكبر من 90 درجة

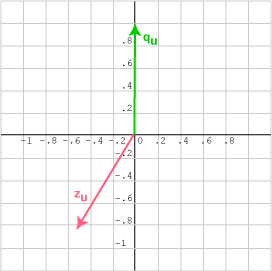
أوجد جيب تمام الزاوية بين شعاعي الوحدة المُمثَّلين بالمصفوفتين ‎q_u = (0.0, 1)^T‎ و ‎z_u = (-0.5, -0.866)^T‎:

الزاوية بين هذين الشعاعين أكبر من 90 درجة، وبالتالي فإن جيب تمام الزاوية بينهما سالبة، حيث cos θ =‫ ‎-0.866، لأن:

θ = arc cos -0.866 = 150‎

الزاوية نفسها تعطي الجداء النقطي نفسه

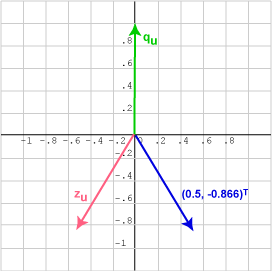
لنحاول الآن رسم الشعاع الآخر الذي جداؤه النقطي مع الشعاع ‎q_u‎ يساوي ‎-0.866 كما يلي:

الشعاعان اللذان يكون ناتج الجداء النقطي لهما مع الشعاع ‎q_u = (0.0, 1)^T‎ يساوي ‎-0.866 هما:

z_u = (-0.5, -0.866)^T

v_u = (0.5, -0.866)^T‎

وضعنا في الرسم البياني السابق ذيل هذين الشعاعين عند نقطة الأصل، ولكن تذكّر أن الأشعة ليست ثابتة في أي موقع معين ويمكن رسمها في أيّ مكان مناسب، وأن الجداء النقطي يعطي الزاوية بين منحى كلٍّ من هذين الشعاعين.

أوجد الزاوية بين الشعاعين: ‎d_u = 0.7071(1,1)^T‎ و ‎e_u = -0.7071(1,1)^T‎، وارسم هذين الشعاعين لتوضيح الحالة:

0.7071‎(1, 1)^T · -0.7071(1, 1)^T = 0.7071(-0.7071)(1+1) = -0.7071² * 2 = -0.5*2 = 1

إذًا الزاوية هي: cos( -1 )‎ =‫ 180 درجة، حيث يوجد شعاع واحد فقط يبعد 180 درجة عن الشعاع المعطى.

تدريب عملي أكثر واقعية

نادرًا ما يمنحك العالم الحقيقي زوايا سهلة تبلغ 30 درجة و 45 درجة و 60 درجة وما إلى ذلك، لذا إليك تدريبًا أكثر واقعية.

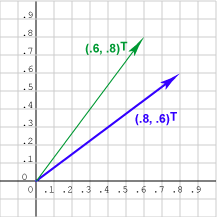
أوجد الزاوية المحصورة بين الشعاعين:

f_u = (0.6, 0.8)^T

g_u = (0.8, 0.6)^T

قد ترغب أولًا في التأكد من أن هذه الأشعة هي أشعة وحدة فعلًا، لذا ارسم هذه الشعاعين، ثم احسب ناتج الجداء النقطي لهما، واستخدم الدالة arc cos في الآلة الحاسبة لحاسوبك (أو الآلة الحاسبة الحقيقية) للعثور على الزاوية، ولا تنسَ حساب الإجابة بالدرجات وليس بالراديان كما يلي:

ناتج الجداء النقطي هو:

‎( 0.6, 0.8 ) · ( 0.8, 0.6 ) = 0.6*0.8 + 0.8*0.6 = 0.48 + 0.48 = 0.96

والزاوية بينهما هي: arc cos( 0.96 )‎ =‫ 16.26 درجة.

الأشعة التي ليست أشعة وحدة

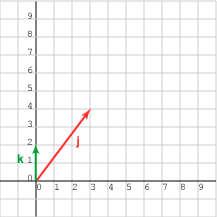
ليكن لدينا الشعاعان التاليان، ونريد إيجاد الزاوية المحصورة بينهما:

j = (3, 4)^T

k = (0, 2)^T

نلاحظ أن هذه الأشعة ليست أشعة وحدة، وبالتالي لا يمكنك العثور على الزاوية بينهما دون مزيد من العمل، لذا دعونا نرسم رسمًا بيانيًا لهما أولًا.

يمكننا إيجاد الزاوية بين هذين الشعاعين من خلال توحيد Normalize كل منهما وهذا لا يغير منحاهما، وبالتالي أصبح لدينا الآن شعاعا وحدة ويمكن إيجاد جيب تمام الزاوية بينهما باستخدام الجداء النقطي.

الزاوية بين الأشعة التي ليست أشعة وحدة

لنوجد الآن الزاوية بين الشعاعين j و k:

نوجد أولًا طول كل شعاع:

| j | = 5.0

| k | = 2.0

ثم نوحّد كلًا منهما، ولكن تذكّر أنه من الحكمة عدم إجراء عملية القسمة في هذه الخطوة في كثير من الأحيان:

j_u = (3, 4)^T / 5.0‎

k_u = (0, 2)^T / 2.0‎

نحسب الآن الجداء النقطي لهما:

j_u · k_u = (3, 4)^T / 5.0 · (0, 2)^T / 2.0 = (1/10)(3, 4)^T · (0, 2)^T = (0.1)(8) = 0.8‎

أخيرًا، نستخدم دالة arc cos في الآلة الحاسبة:

arc cos 0.8 = 36.87 درجة

لنحسب الآن الزاوية المحصورة بين الشعاعين: ‎a = (10, 5)^T‎ و ‎b = (8,12)^T‎ مثلًا.

نحسب الأطوال أولًا:

| a | = √125

| b | = √208

ثم نحسب الجداء النقطي:

‎(10, 5)^T / √125 · (8, 12)^T / √208 = (108 + 512) / ( √125 √208) = 140 / ( √125 √208) = 140 / √(125*208) = 140 / √26000 = 0.86824

وبالتالي فإن الزاوية هي:

arc cos ( 0.86824 ) = 29.745 درجة

وصلنا إلى نهاية هذا المقال الذي يحتوي على قدرٍ كبير من الحسابات لإيجاد الزاوية بين شعاعين في فضاء ثنائي الأبعاد، وسنتعرّف في المقال التالي على كيفية إيجاد الزاوية بين شعاعين في فضاء ثلاثي الأبعاد.

ترجمة -وبتصرُّف- للفصل The Angle between Two Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.