رأينا في المقالات السابقة أن نستطيع استخدام الجداء النقطي Dot Product من أجل الآتي:
- حساب طول الشعاع: حيث يكون الجداء النقطي للشعاع مع نفسه = الطول2.
- اكتشاف التعامد بين شعاعين: حيث يكون الجداء النقطي لشعاعين متعامدين = 0.
- حساب الزاوية بين شعاعين: حيث يكون cosθ = حاصل الجداء النقطي لشعاعي وحدة Unit Vectors.
لن نضيف في هذا المقال شيئًا جديدًا عمّا تعلمناه في المقال السابق، ولكننا سنوسّع مفهوم حساب الزاوية بين شعاعين ليشمل حساب الزاوية بين شعاعين في فضاء ثلاثي الأبعاد.
سنتعرّف في هذا المقال على المواضيع الآتية:
- صيغة حساب جيب تمام Cosine الزاوية بين أشعة الوحدة.
- قائمة بالخطوات التي يجب اتخاذها لتطبيق هذه الصيغة على الأشعة التي ليست أشعة وحدة.
- استخدام الأشعة في مسائل الهندسة الفراغية.
الزوايا في الفضاء ثلاثي الأبعاد
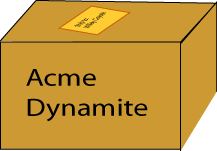
تقع أي حافتين من الحواف الثلاثة المشكّلة لزاوية في صندوق من الورق المقوى في مستوٍ واحد، وتساوي الزاوية بينهما 90 درجة، إذ تتقاطع جميع حواف الصندوق بزوايا قائمة، ولكن لن تساوي الزوايا بين الحواف 90 درجة عادةً عند إسقاط الحواف لتكوين صورة ثنائية الأبعاد.
الزوايا بين محاور الإحداثيات
لا يؤدي تغيير مجال رؤيتك إلى تغيير الكائنات ثلاثية الأبعاد، ولكن ستتغيّر الصورة ثنائية الأبعاد.
تعتمد الزاوية بين شعاعين في الفضاء ثلاثي الأبعاد على علاقتهما ببعضهما البعض، ولا تعتمد على مجال رؤيتك أو إطار الإحداثيات الذي تستخدمه؛ ولكن زوايا الصورة تعتمد كثيرًا على مجال الرؤية عندما تعرض صورة ثنائية الأبعاد مشهدًا ثلاثي الأبعاد.
رأينا في المقال السابق الصيغة التالية لحساب الزاوية θ بين شعاعي الوحدة:
au · bu = cosθ
إذًا لنطبّق هذه الصيغة على شعاعي الوحدة الموازيين للمحور x والمحور y وهما: (1,0,0)T و (0,1,0)T لحساب الزاوية المحصورة بين المحورين x و y كما يلي:
(1,0,0)T · (0,1,0)T = 0
وبالتالي فإن المحورين x و y متعامدان كما توقعنا.
الزاوية بين شعاعين
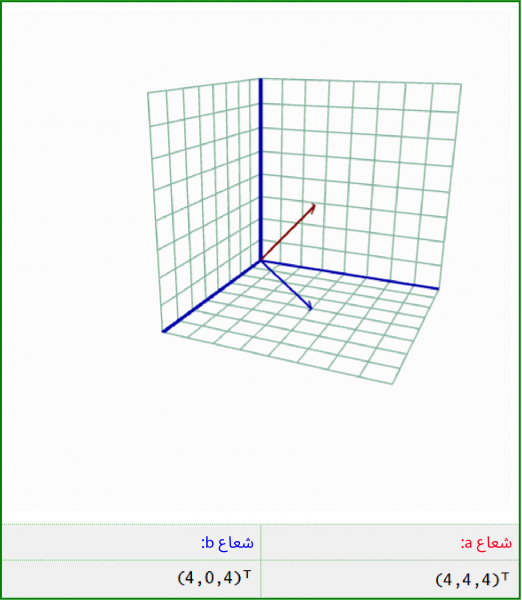
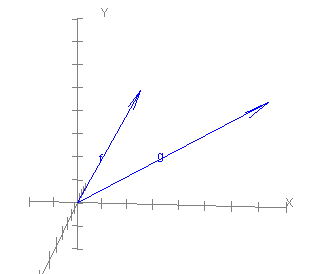
كان المثال السابق سهل التصور والحساب، إذًا لنجرب شيئًا أصعب، حيث يظهر الشكل الآتي شعاعين:
- الشعاع a الذي تمثله المصفوفة العمودية (4,4,4)T.
- الشعاع b الذي تمثله المصفوفة العمودية (4,0,4)T.
لاحظ أن الزاوية بين الشعاعين لا تساوي 90 درجة، وبالتالي يصعب رؤيتها مقارنةً بالمثال السابق.
يمكن أن نخمّن بصريًا إلى حدٍ ما أن الزاوية بين الشعاعين a و b أقل من منتصف المسافة بين المستوي العمودي والأفقي، إذ تكون الزاوية التي تساوي 35 درجة تخمينًا جيدًا، ولكن التخمين غير كافٍ ونحتاج صيغةً لحساب الزاوية، وهذا ما سنوضّحه في الفقرة التالية.
صيغة حساب الزاوية بين شعاعين
لاحظ أنه عند الانتقال من ذيل الشعاع a إلى رأسه تزيد المسافة العمودية بمقدار 4، بينما تزيد المسافة الأفقية بمقدار 4 √2، وظل الزاوية Tangent هو:
4 / (4 √2) = 1.0/ √2 = 0.7071
وبالتالي فإن الزاوية مع المستوي الأفقي هي: arctan( 0.7071 ) = 35.26 درجة. وبما أن الشعاع b يقع في المستوي الأفقي، فإن الزاوية بين الشعاعين يجب أن تساوي هذه القيمة.
وبالتالي فإن صيغة حساب الزاوية θ بين شعاعي وحدة هي:
au · bu = cosθ
ويمكننا استخدام هذه الصيغة مع الأشعة التي ليست أشعة وحدة باتباع الخطوات التالية:
- توحيد Normalize كل شعاع.
- حساب الجداء النقطي لشعاعي الوحدة الناتجين.
- استخدم arc cos للحصول على الزاوية.
لنطبّق هذه الصيغة على الشعاع a الذي تمثله (4,4,4)T والشعاع b الذي تمثله (4,0,4)T كما يلي:
| a | = √(16 + 16 + 16) = 4√3 و | b | = √(16 + 16) = 4√2
au = (4, 4, 4)T / (4√3) و au = (4, 0, 4)T / (4 √2 )
au · bu = (16 + 16)/( (4√3)(4 √2) ) = 2/(√3√2 ) = √2 /√3 = cosθ
cosθ = 0.81649
وبالتالي فإن الزاوية بين الشعاعين هي: θ = 35.26 درجة.
لا تُعَد الحسابات الكثيرة في التمرين السابق هي الغرض الحقيقي، ولكن الهدف هو توضيح الصيغة au · bu = cosθ، والتي تُعَد مهمةً في كل جزء من أجزاء الرسوميات ثلاثية الأبعاد.
تدريب عملي
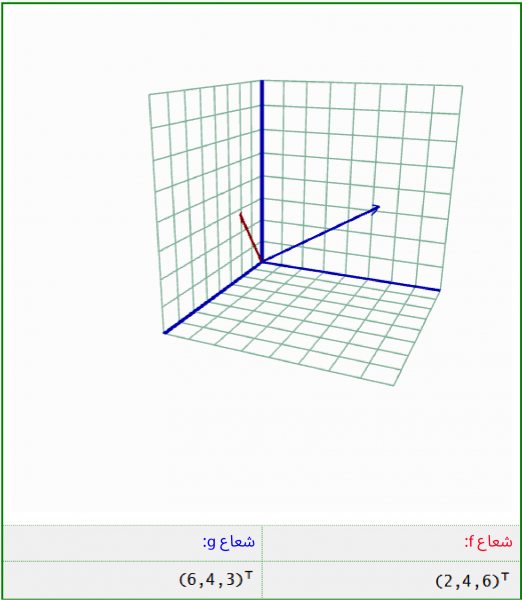
يوضح الشكل الآتي شعاعين تمثّلهما المصفوفتان العموديتان التاليتان:
f = (2, 4, 6)T
g = (6, 4, 3)T
يمكن أن ترغب في قياس الزاوية بين الشعاعين من خلال وضع مِنقلة مسطحة بين الشعاعين، ولكن لا يمكنك ذلك لأن كل ما تراه هو إسقاطٌ للشعاعين على الشاشة.
يمكننا تخمين الزاوية التي تفصل بين الشعاعين بمقدار 30 درجة، ولكنه مجرد تخمين، إذًا لنطبّق الصيغة لمعرفة مدى صحة هذا التخمين.
أولًا، نحسب الأطوال وهي:
| f |2 = (2, 4, 6)T · (2, 4, 6)T = 4 + 16 + 36 = 56
| g |2 = (6, 4, 3)T · (6, 4, 3)T = 36 + 16 + 9 = 61
ثانيًا، نوحّد الشعاعين كما يلي:
fu = (2, 4, 6)T / √56
gu = (6, 4, 3)T / √61
ثالثًا، نحسب الجداء النقطي لهما وهو:
fu · gu = (2, 4, 6)T · (6, 4, 3)T / ( √56 √61) = (12+16+18)/( √56 √61) = 46 / ( √56 √61) = 0.78704
رابعًا، نحسب الزاوية بينهما كما يلي:
cos θ = 0.78704
θ = arc cos 0.78704 = 38.1 درجة
لاحظ أن الجواب ليس بعيدًا جدًا عن التخمين.
الزاوية بين اتجاهي شعاعين
ليس من الضروري أن يتلامس الشعاعان عند ذيليهما حتى تكون هناك زاوية بينهما، فليس للأشعة موضع محدد، إذ يمكنك أخذ الجداء النقطي لأي شعاعين ثلاثي الأبعاد أو المصفوفات العمودية التي تمثلها.
قد يبدو من الغريب قياس الزاوية بين الأشياء التي ليس لها موضع محدد، ولكن العديد من الظواهر لها منحًى Orientation، دون أن يكون لها موضع محدد؛ إذ قد تأتي الرياح من الغرب في أحد الأيام، ومن الشمال في اليوم التالي (بفارق 90 درجة)؛ وقد يصل ضوء الشمس عند الظهيرة في الصيف بزاوية مختلفة عن زاوية وصوله عند الظهيرة في الشتاء. يستخدم التظليل في الرسوميات ثلاثية الأبعاد أشعةً لمنحى السطح، وأشعة أخرى لاتجاه كل مصدر للضوء.
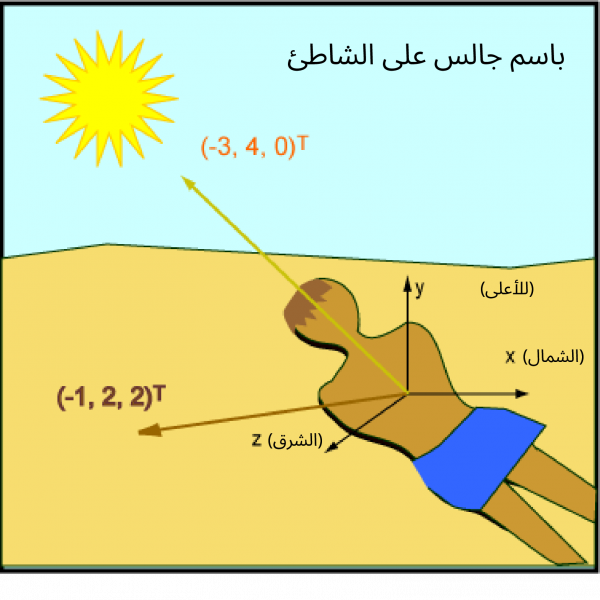
ليكن باسم وبلال جالسين على الشاطئ، ويريدان تسمير بشرتهما كما في الشكل التالي:
يؤشر إطار الإحداثيات المناسب إلى المحور x شمالًا، والمحور y للأعلى بصورة مستقيمة والمحور z شرقًا، حيث يكون الاتجاه نحو الشمس في هذا الإطار هو (-3, 4, 0)T / 5، وشعاع الوحدة العمودي على ظهر باسم هو ( -1, 2, 2)T / 3، وشعاع الوحدة العمودي على ظهر بلال هو ( -2, 1, 2)T / 3.
إذًا سيكون أحدهما متمتعًا بأفضل موضع للتسمير السريع، حيث سنوضّح ذلك كما يلي:
- الاتجاه نحو الشمس = ( -3, 4, 0)/5.
- الاتجاه العمودي على ظهر باسم = ( -1, 2, 2)/3.
- الاتجاه العمودي على ظهر بلال = ( -2, 1, 2)/3.
يجب أن يكون ظهرك مُوجَّهًا مباشرةً نحو الشمس ليصل إليك أكبر قدرٍ من أشعتها، كما يجب أن تكون الزاوية بين الاتجاه العمودي على ظهرك واتجاه الشمس صغرى.
بالنسبة لباسم:
( -1, 2, 2)/3 · ( -3, 4, 0)/5 = (3+8+0)/15 = 11/15
arc cos( 11/15 ) = 42.8 درجة
وبالنسبة لبلال:
( -2, 1, 2)/3 · ( -3, 4, 0)/5 = (6+4+0)/15 = 10/15
arc cos( 14/15 ) = 48.2 درجة
وبالتالي سيحصل باسم على تسمير لبشرته بصورة أسرع.
تدريبات عملية
تدريب 1:
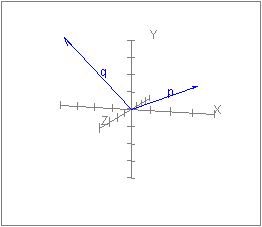
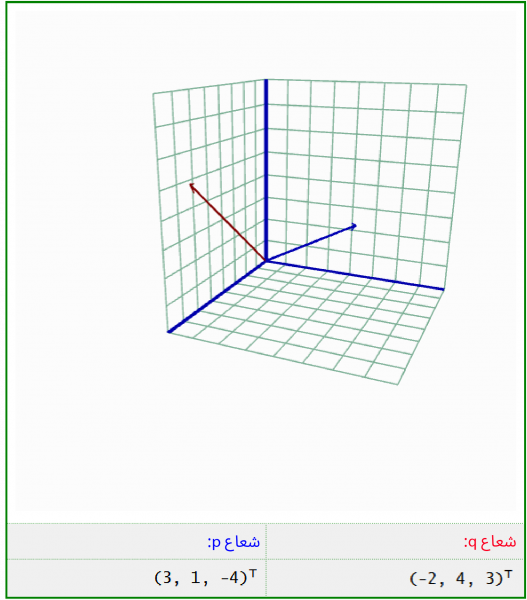
يظهر الرسم البياني الآتي الشعاعين التاليين:
q = (-2, 4, 3)T
p = (3, 1, -4)T
وضعنا ذيل الأشعة عند نقطة الأصل لسهولة التصور، إذ تؤشّر الأشعة إلى ثُمنَين Octants مختلفتين من الفضاء ثلاثي الأبعاد.
لنحسب الآن الزاوية بين هذين الشعاعين كما يلي:
أولًا، نحسب الأطوال وهي:
| p |2 = ( -2, 4, 3)T · ( -2, 4, 3)T = 4 + 16 + 9 = 29
| q |2 = ( 3, 1, -4)T · ( 3, 1, -4)T = 9 + 1 + 16 = 26
ثانيًا، نوحّد الشعاعين كما يلي:
pu = (-2, 4, 3)T / √29
qu = (3, 1, -4)T / √26
ثالثًا، نحسب الجداء النقطي لهما وهو:
pu · qu = (-2, 4, 3)·(3, 1, -4)T / ( √29 √26) = (-6 + 4 - 12)/( √29 √26) = -14/( √29 √26) = -0.50985
رابعًا، نحسب الزاوية بينهما كما يلي:
cos θ = -0.50985
θ = arc cos( -0.50985) = 120.654 درجة
تدريب2:
أوجد جيب تمام الزاوية بين شعاعي الوحدة التاليين:
s = (1, 0, 1)T /√2
t = (1, 1, 1)T /√3
cosθ = (1, 0, 1)T · (1, 1, 1)T / ( √2 √3) = 2 / ( √2 √3) = √2 / √3 = 0.8164
استخدام صيغة الجداء النقطي لحل المسائل الهندسية
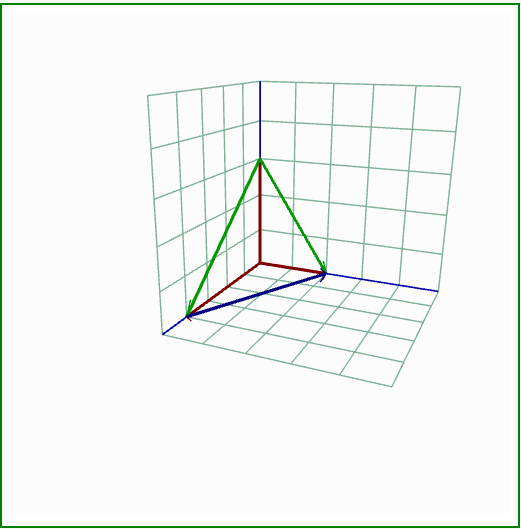
يمكن استخدام صيغة الجداء النقطي لحل بعض المسائل الهندسية التي قد تكون صعبة الحل، فمثلًا، تتطابق الحواف الحمراء في الشكل التالي على محاور الإحداثيات، وتشترك في نقطة النهاية (0, 0, 0)، وتنتهي الحافة على طول المحور x عند x=2، وتنتهي الحافة على طول المحور y عند y=3، وتنتهي الحافة على طول المحور z عند z=4، وتربط الحواف المتبقية نقاط النهاية هذه.
لنفترض الآن أنك تريد حساب الزاوية بين الحافتين الخضراويتين، وقد يكون ذلك مملًا إلى حدٍ ما باستخدام علم المثلثات، لذا يمكنك:
- تشكيل شعاع لكل حافة خضراء (من خلال طرح نقاط النهاية).
- توحيد كل شعاع منهما.
- استخدام قاعدة الجداء النقطي لحساب الزاوية بينهما.
إذًا لنطبّق هذه الخطوات لحساب الزاوية بين الحافتين الخضراويتين كما يلي:
أولًا، نقاط النهاية هي:
(0, 3, 0) إلى (2, 0, 0)
(0, 3, 0) إلى (0, 0, 4)
ثانيًا، نحسب أشعة الإزاحة وهي:
a = (2, 0, 0) - (0, 3, 0) = (2, -3, 0)T
b = (0, 0, 4) - (0, 3, 0) = (0, -3, 4)T
ثالثًا، نحسب الأطوال كما يلي:
| a |2 = (2, -3, 0)T · (2, -3, 0)T = 13
| b |2 = (0, -3, 4)T · (0, -3, 4)T = 25
رابعًا، نوحّد الأشعة كما يلي:
au = (2, -3, 0)T / √13
bu = (0, -3, 4)T / 5
خامسًا، نحسب الجداء النقطي لهما:
au · bu = (2, -3, 0)T · (0, -3, 4)T / (5 √13) = 9 / (5 √13) = 0.49923
سادسًا، نحسب الزاوية بينهما كما يلي:
cosθ = 0.49923
θ = arc cos 0.49923 = 60.051 درجة
إذا حسبتَ أشعة الإزاحة بالطريقة المعاكسة (بالطرح من (0, 3, 0))، فلن يؤثر ذلك على الإجابة، إذ يمكن أن يؤشّر شعاعان إلى اتجاهين متعاكسين، ولكن حاصل جدائهما النقطي سيكون نفسه.
بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية حساب الزاوية بين شعاعين في فضاء ثلاثي الأبعاد، وسنتعرّف في المقال التالي على إسقاط شعاعٍ ما على شعاع آخر.
ترجمة -وبتصرُّف- للفصل The Angle between 3D Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.










أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.