تُستخدَم المصفوفات في العديد من المجالات لتمثيل كلٍّ من الكائنات والعمليات التي تُطبَّق عليها؛ إذ تُمثَّل النقاط والأشعة بالمصفوفات العمودية في الرسوميات الحاسوبية، وتُمثَّل العمليات عليها بمصفوفات مربّعة.
سنناقش في هذا المقال المواضيع التالية:
- تعريف المصفوفة.
- عناصر المصفوفة.
- أبعاد المصفوفة.
- أسماء المصفوفات.
- تَساوي مصفوفتين.
- المصفوفة المربعة.
- عملية جمع المصفوفات وقواعدها.
- المصفوفة الصفرية.
- معاكس مصفوفة.
- طرح المصفوفات.
- ضرب المصفوفات بعدد حقيقي Scalar.
- منقول Transpose المصفوفة.
تعريف المصفوفة
تتكوّن المصفوفة العمودية من عمود واحد من الأعداد، ولكن يمكن ترتيب هذه الأعداد في عدة صفوف وعدة أعمدة، وبالتالي يمكن وضع الأعداد في مصفوفة ثنائية الأبعاد. إذًا المصفوفة هي مجموعة من الأعداد المرتَّبة ضمن عددٍ ثابت من الصفوف والأعمدة، وتكون هذه الأعداد أعدادًا حقيقية.
يمكن أن تحتوي المصفوفات على أعداد معقدة أيضًا، ولكننا لن نراها في هذا المقال.
إليك مثالًا لمصفوفة مكونة من ثلاثة صفوف وثلاثة أعمدة:
الصف العلوي هو الصف 1، والعمود الموجود في أقصى اليسار هو العمود 1، والمصفوفة السابقة هي مصفوفة بحجم 3x3، لأنها تحتوي على ثلاثة صفوف وثلاثة أعمدة، ويكون التنسيق لوصف المصفوفات هو: rows X columns.
يسمّى كل عدد يشكّل المصفوفة عنصرًا Element من عناصرها، ويكون للعناصر مواقع مُحدَّدة في المصفوفة؛ إذ تمثّل الزاويةُ العلوية اليسرى من المصفوفة الصفَّ 1 والعمود 1، وقيمة العنصر الموجود في الصف 1 والعمود 1 في المصفوفة السابقة هي 1، وقيمة العنصر الموجود في الصف 2 والعمود 3 هي 4.6، وقيمة العنصر في الصف 3 والعمود 1 هي 4.
أبعاد المصفوفة
يُطلَق مصطلح أبعاد المصفوفة على عدد صفوفها وأعمدتها. إليك فيما يلي مصفوفةً مكونةً من ثلاثة صفوف وعمودين:
تُكتَب أحيانًا الأبعاد إلى جانب المصفوفة كما هو الحال في المصفوفة السابقة، ولكنه مجرد تذكير صغير وليس جزءًا من المصفوفة. إليك مثالًا آخر لمصفوفة ذات أبعاد مختلفة تتكون من صفين وثلاثة أعمدة، والتي تُعَد "نوع بيانات" مختلف عن المصفوفة السابقة:
المصفوفة المربعة Square Matrix
تحتوي المصفوفة المربعة Square Matrix على العدد نفسه من الصفوف والأعمدة، وتُستخدَم المصفوفات المربعة لتمثيل التحويلات الهندسية Transformations في الرسوميات الحاسوبية.
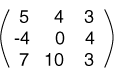
المصفوفة المستطيلة Rectangular Matrix هي المصفوفة التي يمكن ألّا يكون لها العدد نفسه من الصفوف والأعمدة. مع ذلك، تطالب بعض المراجع بوجوب أن يكون عدد الصفوف مختلفًا عن عدد الأعمدة.
أما المصفوفة العمودية Column Matrix فتتكون من عمود واحد، وهي مصفوفة بحجم N x 1، وقد استخدمنا المصفوفة العمودية في هذه السلسلة من المقالات لتمثيل الأشعة الهندسية مثل معظم كتب الرسوميات الحاسوبية. إليك مثالًا عن مصفوفة عمودية بحجم :4 x 1
تتكون المصفوفة السطرية Row Matrix من صفٍ واحد، حيث تستخدم بعض الكتب المصفوفات السطرية لتمثيل الأشعة الهندسية. تسمّي بعض الكتب المصفوفة العمودية بالشعاع العمودي وتسمّي المصفوفة السطرية بالشعاع السطري، ويُعَد ذلك أمرًا جيدًا، ولكنه غامضٌ بعض الشيء، لذا سنستخدم في هذا المقال مصطلح شعاع Vector للتعبير عن كائن هندسي، وسنستخدم المصفوفات العمودية لتمثيل الأشعة، كما سنستخدمها أيضًا لتمثيل النقاط الهندسية.
أسماء المصفوفات
إذا نسيت ما إذا كانت الصفوف أو الأعمدة تأتي أولًا، فتذكر فقط مصطلح الأعمدة الرومانية ROWman COLumns.
يمكن إعطاء اسمٍ للمصفوفة، ويكون هذا الاسم عادةً حرفًا إنجليزيًا كبيرًا بخط عريض في النصوص المطبوعة مثل A أو M، وتُكتَب في بعض الأحيان الأبعاد على يمين الحرف كما في المصفوفة B3x3.
لعناصر المصفوفة أسماءٌ أيضًا؛ إذ يكون اسم العنصر عادةً بحرفٍ مماثل لاسم المصفوفة، ولكنه حرفٌ صغير مع كتابة موضع العنصر بصورة منخفضة، لذلك يمكن مثلًا كتابة المصفوفة A التي أبعادها 3x3 على النحو التالي:
يمكن أيضًا كتابة المصفوفة A = [aij] للقول بأن عناصر المصفوفة A تسمَّى aij.
تساوي مصفوفتين
إذا احتوت مصفوفتان على القيم نفسها، ولكن في مواقع مختلفة، فلا يمكن عَدّ هاتين المصفوفتين متساويتين، فلكي تكون المصفوفتان متساويتان، يجب أن يكون:
- لهما الأبعاد نفسها.
- يجب أن تكون العناصر المتقابلة متساوية.
لنفترض أن لدينا المصفوفتين A n x m = [aij] و B p x q = [bij]، وعندها يكون A = B إذا وفقط إذا كان n=p و m=q وaij=bij لجميع قيم i و j ضمن المجال المحدَّد.
إليك مصفوفتين غير متساويتين بالرغم من أنهما تحتويان على العناصر نفسها:
كما أن المصفوفتين التاليتين غير متساويتين، لأن عناصرهما المتقابلة غير متساوية بالرغم من لهما الأبعاد نفسها:
جمع المصفوفات
إذا كانت لدينا مصفوفتان لهما العدد نفسه من الصفوف والأعمدة، فيمكن حساب مجموعهما؛ حيث إذا كانت A مصفوفةً أبعادها MxN، وكانت B مصفوفةً أبعادها MxN، فإن مجموعهما هو مصفوفة أبعادها MxN مكوّنة من جمع العناصر المتقابلة للمصفوفتين A و B.
إليك مثال عن جمع مصفوفتين:
تكون عناصر المصفوفات أعدادًا حقيقية ذات كسور عشرية في معظم الحالات العملية، وليست أعدادًا صحيحة صغيرة كتلك المستخدمة غالبًا في أمثلتنا.
المصفوفة الصفرية Zero Matrix
يمكن جمع مصفوفة أبعادها 3x2 مع مصفوفة أخرى أبعادها 3x2 دون تغيير المصفوفة الثانية إذا كانت جميع عناصر المصفوفة الأولى أصفارًا، والتي تُسمَّى بالمصفوفة الصفرية. إليك مثال عن مصفوفة صفرية أبعادها 3x3:
اسم المصفوفة الصفرية هو صفر مكتوب بخط عريض 0، بالرغم من أننا قد ننسى في بعض الأحيان كتابته بخط عريض.
أوجد ناتج عملية الجمع التالية:
المجموع بالطبع هو المصفوفة غير الصفرية نفسها.
قواعد جمع المصفوفات
سنوضّح فيما يلي قواعد جمع المصفوفات، إذ يفترض أن تكون للمصفوفات الأبعاد نفسها:
A + B = B + A
A + 0 = 0 + A = A
0 + 0 = 0
تشبه هذه القواعد بعض القواعد الخاصة بجمع الأعداد الحقيقية، ولكن انتبه إلى أنه ليست جميع قواعد رياضيات المصفوفات مماثلة لتلك الخاصة برياضيات الأعداد الحقيقية.
تنص القاعدة الأولى على أن جمع المصفوفات هو عملية تبديلية Commutative، بسبب إجراء عملية الجمع العادي على العناصر المتقابلة في المصفوفتين، ويُعَد الجمع العادي (الحقيقي) تبديليًا.
كما يُعَد جمع المصفوفات عملية تجميعية Associative، وهي قاعدة أخرى تماثل قواعد رياضيات الأعداد الحقيقية، بسبب إجراء عملية الجمع العادية على العناصر المتقابلة من المصفوفتين:
(A + B) + C = A + (B + C)
لنوجِد ناتج جمع المصفوفتين التاليتين:
لاحظ أن كل عنصر من عناصر المصفوفة الناتجة التي أبعادها 3x3 هو 10.
ضرب المصفوفة بعدد حقيقي Scalar
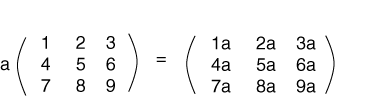
يمكن ضرب المصفوفة بعدد حقيقي (مقدار سلمي) من خلال ضرب كل عنصر من عناصر المصفوفة بهذا العدد. إليك مثال على ذلك، بحيث يكون المتغير a عددًا حقيقيًا:
يكون كل عنصر في النتيجة معاكسًا للعنصر الأصل إذا كانت قيمة العدد الحقيقي a في المثال السابق تساوي -1، كما سنرى في الفقرة التالية.
معاكس المصفوفة
يمكن تشكيل معاكس للمصفوفة من خلال تغيير إشارة كل عنصر من عناصر هذه المصفوفة:
-A = -1 A
كما في المثال التالي:
تنتج المصفوفة الصفرية عن جمع المصفوفة مع معاكسها. لاحظ أن الصفر الأخير هو صفر بخط عريض، والذي يعبّر عن المصفوفة الصفرية:
A + (-A) = 0
ملاحظة: يمكن تعريف عملية الطرح مصفوفتين على أنها عملية جمع المصفوفة الأولى مع معاكس المصفوفة الثانية.
طرح المصفوفات
إذا كانت المصفوفتان A و B لهما العدد نفسه من الصفوف والأعمدة، فيمكن تعريف عملية الطرح A - B بأنها A + (-B)؛ إذ يمكن حساب A - B من خلال طرح العنصر المقابل من المصفوفة B من كل عنصر من عناصر المصفوفة A.
إليك مثال غير مكتمل عن طرح المصفوفات:
لاحظ العناصر الموجودة في الصف الأول من الإجابة السابقة؛ إذ تُعَد طريقة حساب النتيجة للعناصر الموجودة في الصف 1 والعمود 2 مربكةً بعض الشيء.
لنحاول الآن وضع الإجابة مكان علامتي الاستفهام في المثال السابق كما يلي:
منقول مصفوفة Transpose
منقول المصفوفة هو مصفوفة جديدة تكون صفوفها هي أعمدة المصفوفة الأصلية، مما يؤدي أيضًا إلى جعل أعمدة المصفوفة الجديدة هي صفوف المصفوفة الأصلية. إليك مثال عن مصفوفة ومنقولها:
الحرف المرتفع "T" يعني المنقول "Transpose".
هناك طريقة أخرى للنظر إلى المنقول، وهي أن العنصر الموجود في الصف r والعمود c في المصفوفة الأصلية يُوضَع في الصف c والعمود r من المنقول؛ إذ يصبح العنصرُ arc في المصفوفة الأصلية هو العنصر acr في المصفوفة المنقولة.
نتعامل عادةً مع المصفوفات المربعة لإيجاد منقولها، ولكن يمكن نقل المصفوفات غير المربعة أيضًا مثل المصفوفة التالية:
إليك مثال آخر عن كيفية إيجاد منقول مصفوفة غير مربعة:
قاعدة خاصة بمنقول المصفوفة
إذا أوجدنا المنقول لمنقول المصفوفة نفسها، فستحصل على المصفوفة الأصلية مرةً أخرى كما في المثال التالي:
ويوضح المثال السابق القاعدة: (AT)T = A.
لاحظ أن منقول مصفوفة سطرية هو مصفوفة عمودية، وبالتالي فإن منقول مصفوفة عمودية هو مصفوفة سطرية كما في المثال التالي:
المصفوفة المتناظرة Symmetric Matrix
المصفوفة المتناظرة هي المصفوفة التي تتساوى مع منقولها، أي: AT = A، ولكن يجب أن تكون مصفوفةً مربعة. إليك فيما يلي مثال عن بعض المصفوفات المتناظرة:
إذا كانت المصفوفة متناظرة، فستكون عناصرها aij = aji.
ملاحظة: تُعَد المصفوفة الصفرية مصفوفةً متناظرةً أيضًا.
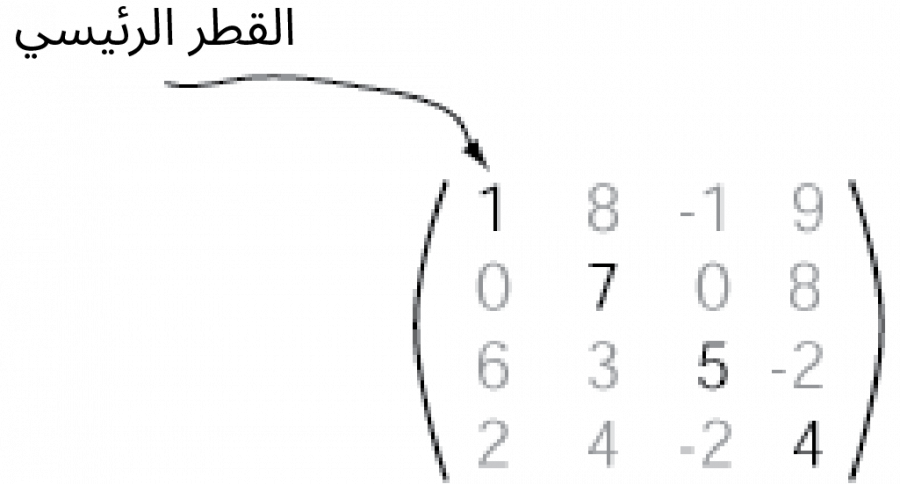
قطر المصفوفة الرئيسي Main Diagonal
يتكوّن القطر الرئيسي للمصفوفة من العناصر التي تقع على القطر الذي يمتد من أعلى يسار المصفوفة إلى أسفل يمينها، فإذا كانت لدينا المصفوفة A مثلًا، فإن عناصر قطرها الرئيسي هي العناصر التي يتساوى فيها رقم الصف مع رقم العمود ajj.
لا يُعَد القطر الآخر للمصفوفة مهمًا وليس له اسم.
ملاحظة: عناصر المصفوفة A التي لا تتغير عند تشكيل المنقول AT، هي العناصر الموجودة على طول القطر الرئيسي، لأن العناصر ajj في المصفوفة A هي العناصر نفسها في المنقول AT.
الخلاصة
إليك بعض القواعد التي ناقشناها في هذا المقال؛ إذ يجب عليك فهمها بدلًا من حفظها، حيث تحتوي المصفوفات في كل قاعدة من القواعد التالية على العدد نفسه من الصفوف والأعمدة:
- A + 0 = A
- A + B = B + A
- 0 + 0 = 0
- A + (B + C) = (A + B) + C
- (ab) A = a(b A)
- a(A + B) = a B + a A
- a 0 = 0
- (-1) A = -A
- A - A = 0
- (AT)T = A
- 0T = 0
حيث أن a و b هي مقادير سلمية (أعداد حقيقية)، و A و B مصفوفتان، و 0 هي المصفوفة الصفرية ذات البعد المناسب.
ملاحظة: إذا كان A = B و B = C، فإن A = C.
وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على المصفوفات وعملياتها البسيطة، وسنناقش في المقال التالي مزيدًا من الأمور التي يمكن تطبيقها باستخدام المصفوفات.
ترجمة -وبتصرُّف- للفصل Matrices and Simple Matrix Operations من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.


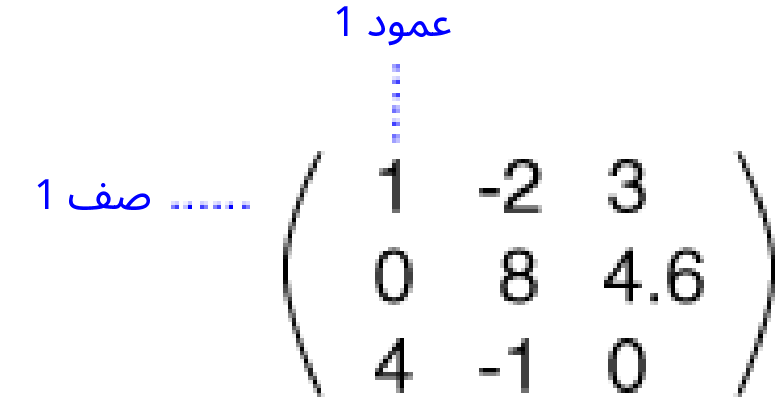
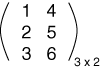
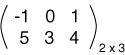
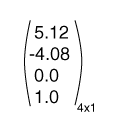
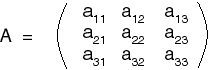
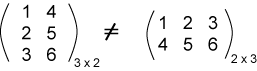
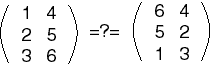
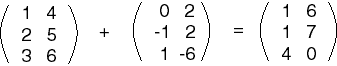
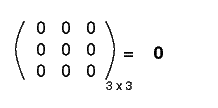
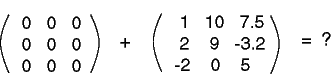


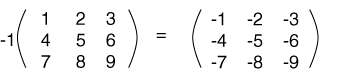
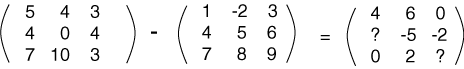
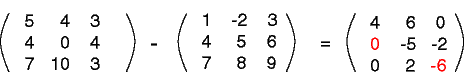
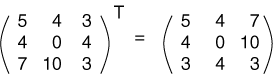
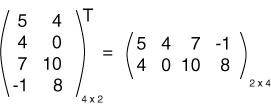
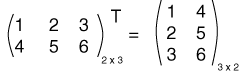
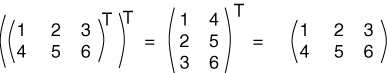
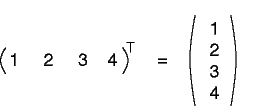












أفضل التعليقات
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.