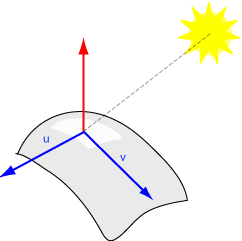
يُعَد الجداء الشعاعي عمليةً تستخدم شعاعين على أساس معامَلين. وتكمن أهمية هذا في الرسوميات الحاسوبية عند محاولة العثور على شعاع عمودي على مستوٍ؛ ويُعَد ذلك ضروريًا عند حساب كيفية انعكاس الضوء على السطوح.
سنوضّح في هذا المقال المواضيع التالية:
- تعريف الجداء الشعاعي لشعاعين.
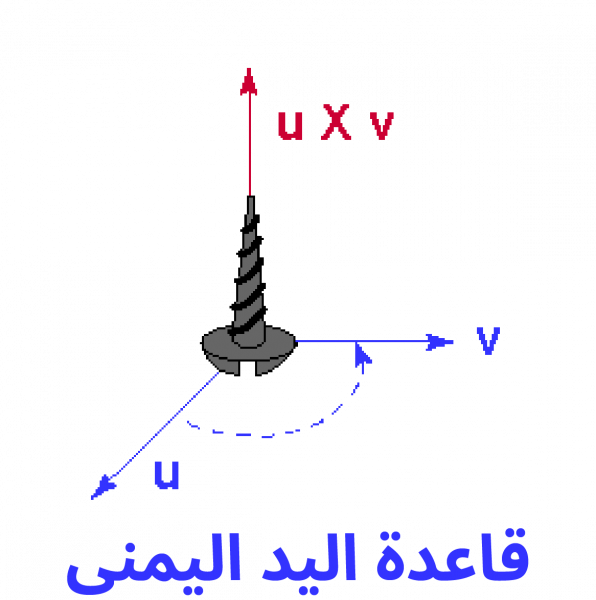
- قاعدة اليد اليمنى: يكون منحى Orientation الجداء الشعاعي u × v باتجاه "الإبهام" إذا طويت أصابعك من الشعاع u إلى الشعاع v.
- خاصيات الجداء الشعاعي والتي هي:
- حجم Magnitude الجداء الشعاعي: حجم الجداء الشعاعي u × v هو مساحة متوازي الأضلاع التي يحدّدها هذان الشعاعان.
- لا يُعَد الجداء الشعاعي عملية تبديلية Anti-commutative:
u × v = -(v × u)
u × u = 0 و (ku) × u = 0
- نتيجة الجداء الشعاعي لشعاع مع شعاع صفري هي شعاع صفري:
u × 0 = 0 × u = 0
- لا يُعَد الجداء الشعاعي عملية تجميعية:
(u × v) × w ≠ u × (v × w)
- إمكانية توزيع الجداء الشعاعي على جمع الأشعة:
u × (v + w) = u × v + u × w
- الجداء الشعاعي بين محاور الإحداثيات:
i × j = k و j × k = i و k × i = j
- حساب الجداء الشعاعي باستخدام المصفوفات العمودية.
- استخدام أداة مساعدة شبيهة بمحدّدات المصفوفات Determinant لتذكّر صيغة حساب الجداء الشعاعي للمصفوفات العمودية.
تذكير: يكون نوع الكائنات التي تمثّلها معامَلات الجداء النقطي أشعةً، وتكون نتيجة الجداء النقطي عددًا حقيقيًا (مقدارًا سلميًا) Scalar.
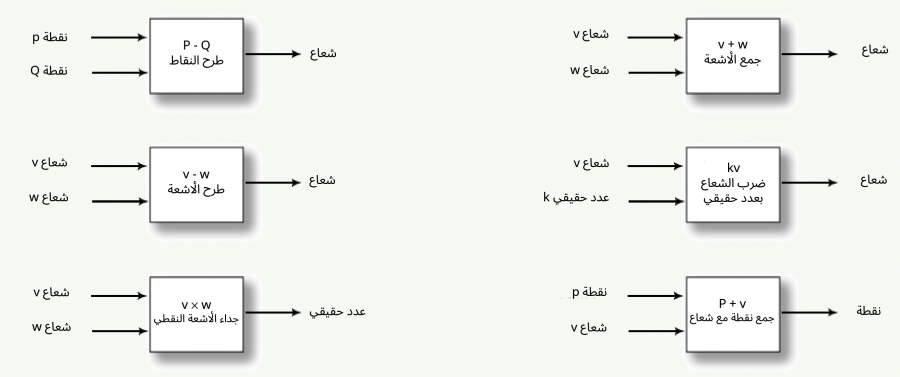
لقد شاهدت حتى الآن العمليات التالية:
ولكن لا توجد عملية تشبه الضرب وتأخذ شعاعين كمعامَلين وينتج عنها شعاع، وهذا ما يمثله جداء الأشعة الشعاعي الذي سنشرحه في هذا المقال.
تعريف الجداء الشعاعي
إذا كان u و v شعاعين في فضاء ثلاثي الأبعاد، فإن الجداء الشعاعي لهما u × v هو شعاع ثلاثي الأبعاد، ويجب أن تكون معاملات هذه العملية ونتيجتها أشعةً ثلاثية الأبعاد على عكس العمليات الأخرى؛ إذ أن عملية الجداء الشعاعي ليست مُعرَّفةً في الفضاء ثنائي الأبعاد 2D.
يمكن تعريف الجداء الشعاعي لشعاعين u × v كما يلي:
- يجب أن يكون u و v شعاعين ثلاثي الأبعاد.
-
والنتيجة هي شعاع ثلاثي الأبعاد مع الطول والمنحى التاليين:
- الطول: | u × v | = | u | | v | sin θ حيث θ هي الزاوية بين الشعاعين u و v.
- المنحى: يكون ناتج الجداء الشعاعي u × v عموديًا على كلٍّ من الشعاعي u و v.
- يجري الاختيار من بين منحيين متعامدين على الشعاعين u و v باستخدام قاعدة اليد اليمنى.
ناتج الجداء الشعاعي لشعاعين هو شعاع عمودي على هذه الشعاعين، ولكن هناك اتجاهين متعامدين على كلٍّ من هذين المعامَلين، حيث يمكن الاختيار من بينهما باستخدام قاعدة اليد اليمنى، والتي سنشرحها في الفقرة التالية.
قاعدة اليد اليمنى Right-hand Rule
نضع البرغي الخشبي عموديًا على لوحٍ من الخشب، ونلفّه باتجاه اللوح الخشبي باستخدام مفك براغي؛ إذ يجب أن ندير البرغي اليميني (النوع العادي) باتجاه عقارب الساعة من رأسه إلى اللوح الخشب.
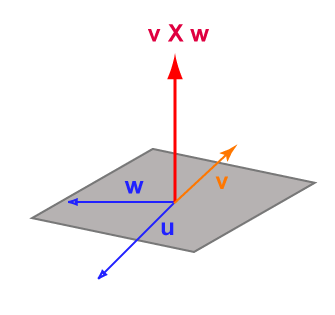
يكون الجداء الشعاعي لشعاعين متعامدًا عليهما، وتختار قاعدة اليد اليمنى أحد الاتجاهين المتعامدين المُحتمَلين. ويوضح الرسمان البيانيان السابقان هذه القاعدة.
لا تنسَ أن ترتيب المعاملات مهم، إذ تؤشّر نتيجة الجداء الشعاعي u × v إلى الاتجاه نفسه الذي يجب أن يؤشّر إليه البرغي، إذا دفع الالتفافُ من الشعاع u إلى الشعاع v البرغي إلى داخل قطعة الخشب، أو فكّر في الاتجاه الذي يؤشّر إليه إبهامك عندما تطوي أصابعك من الشعاع u إلى الشعاع v.
ملاحظة: يؤشّر الجداء الشعاعي u × v و v × u إلى اتجاهين متعاكسين.
تصور الجداء الشعاعي
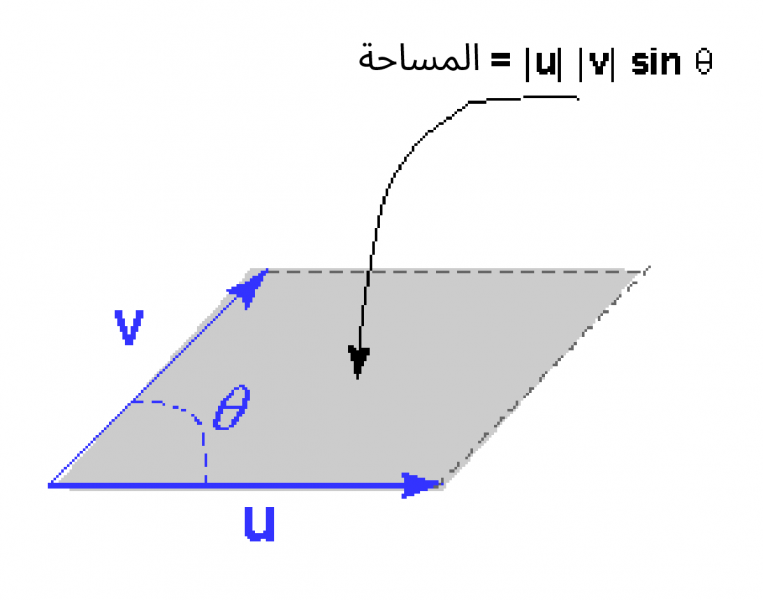
يُظهر الشكل التالي الشعاعين u و v ومتوازي الأضلاع المُحدَّد بينهما.
مساحة متوازي الأضلاع هي: | u | | v | sin θ، حيث θ هي الزاوية بينهما.
تمثّل هذه المساحة حجم الجداء الشعاعي، وتكون هذه الحقيقة مفيدةً أحيانًا لتصور الجداء الشعاعي، فإذا دوّرنا الشعاع u مثلًا، بحيث يقترب منحاه من منحى الشعاع v (دون تغيير طوله)، فستقترب مساحة متوازي الأضلاع وحجم الجداء الشعاعي من الصفر، بينما تعطي الزاوية 90 درجة بين الشعاعين u و v القيمة العظمى للجداء الشعاعي.
عكس ترتيب معاملات الجداء الشعاعي
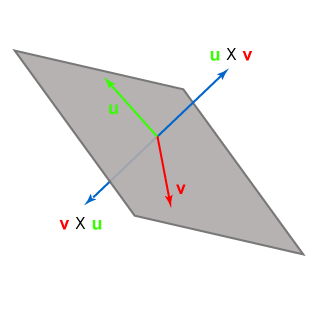
تذكير: يمكن عكس اتجاه الشعاع w من خلال ضربه بالعدد -1؛ إذ يؤشّر الشعاعان w و -w إلى اتجاهين متعاكسين.
يوضح الشكل السابق حاصل عمليتي جداء شعاعين حدّدنا منحاهما باستخدام قاعدة اليد اليمنى، ويكون حجم الجداء الشعاعي:
u × v = | u | | v | sin θ = | v | | u | sin θ
وبالتالي:
u × v = -(v × u)
ويمكن القول أن:
-(v × u) = -v × u
المعاملات المتوازية للجداء الشعاعي
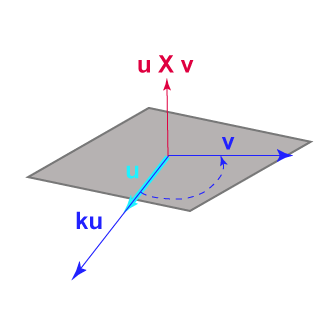
طول u × v هو | u | | v | sin θ، وإذا كان u و v شعاعين على استقامة واحدة Collinear (متوازيين)، فإن الزاوية بينهما θ = 0، وبالتالي سيكون sin θ = 0، وحجم ناتج الجداء الشعاعي يساوي الصفر، ولكن النتيجة هي شعاع؛ وبالتالي تكون نتيجة الجداء الشعاعي هي الشعاع الصفري 0.
u × u = 0
بما أن k u على استقامة واحدة مع الشعاع u (حيث k عدد حقيقي)، فسيكون:
(k u) × u = 0
نتيجة الجداء الشعاعي u × u = 0 عمودية على كلا المعامَلين، لأن 0 · u = 0، مما يعني أنهما متعامدان؛ فالشعاع الصفري 0 عمودي على جميع الأشعة كما مر معنا سابقًا.
حجم الجداء الشعاعي u × 0 وهو | u | | 0 | sin θ يساوي الصفر، والنتيجة هي شعاع، وبالتالي:
u × 0 = 0 × u = 0
لنوجد الآن الجداء الشعاعي (k u) × v من خلال الاطلاع على الرسم البياني السابق، أو من خلال العمل بالصيغة التالية:
(k u) × v = k( u × v )
وسينتج ما يلي:
| (k u) × v | = | k u | | v | sin θ = | k | | u | | v | sin θ
إذًا يكون حجم (k u) × v أكبر بمقدار | k | عن حجم u × v مع إبقاء الاتجاه نفسه.
ليس الجداء الشعاعي للأشعة عملية تجميعية
لا يُعَد الجداء الشعاعي للأشعة عمليةً تجميعية، ويمكن رؤية ذلك من خلال النظر إلى الرسم البياني السابق، ثم تشكيل الجداء الشعاعي (u × v)، ثم إجراء الجداء الشعاعي للناتج مع الشعاع w. نشكّل بعد ذلك حاصل الجداء الشعاعي (v × w)، ثم نجري الجداء الشعاعي للناتج مع الشعاع u؛ وينتج لدينا ما يلي:
(u × v) × w ≠ u × (v × w)
لاحظ أن ناتج الجداء الشعاعي للشعاعين u × v من الرسم البياني السابق يساوي الشعاع الصفري 0، لأنهما على استقامة واحدة.
إمكانية توزيع الجداء الشعاعي على جمع الأشعة
توجد خاصية أخرى للجداء الشعاعي، وهي إمكانية توزيع الجداء الشعاعي على عملية جمع الأشعة كما يلي:
u × (v + w) = u × v + u × w
ويمكن الوصول إلى هذه الخاصية من خلال التعويض في الصيغة التي تعرّف الجداء الشعاعي.
الجداء الشعاعي بين محاور الإحداثيات
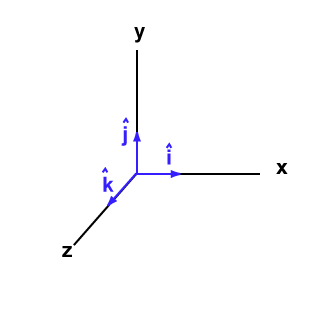
تسمَّى أشعة الوحدة Unit Vectors التي تكون باتجاه المحاور x و y و z (في أيّ إطار إحداثي مُستخدَم)، i و j و k في أغلب الأحيان، وتوضَع أحيانًا قبعات صغيرة على كل حرف كما في الشكل التالي:
بما أن طول كل شعاع من هذه الأشعة يساوي 1، وهي أشعة متعامدة فيما بينها، فإن جيب Sine الزاوية بين أيّ شعاعين منها يساوي 1.0، وستكون الصيغ التالية صحيحة:
i × j = k
j × k = i
k × i = j
i × k = - j
k × j = - i
j × i = - k
i × i = 0
j × j = 0
k × k = 0
ولكن يُفضَّل رسم الرسم البياني ثم استخدام قاعدة اليد اليمنى بدلًا من حفظها.
الجداء الشعاعي للمصفوفات العمودية
نعرّف الجداء الشعاعي لمصفوفتين عموديتين u × v كما يلي:
-
يجب أن تمثّل المصفوفتان العموديتان u و v أشعة ثلاثية الأبعاد.
-
تمثّل النتيجة شعاعًا ثلاثي الأبعاد.
-
إذا مثّلنا الشعاع u بالمصفوفة العمودية:
u = (ui, uj, uk)T
-
ومثّلنا الشعاع v بالمصفوفة العمودية:
v = (vi, vj, vk)T
-
فإن:
u × v = ( uj vk - uk vj, uk vi - ui vk , ui vj - uj vi )T
ملاحظة: لا تفكر في حفظ النتيجة السابقة، بل حاول إيجاد نمط محدّد لتشكيلها.
لنوجد الآن الجداء الشعاعي (1, 2, 3)T × (0, 0, 0)T:
لاحظ أن:
(1, 2, 3)T × 0 = 0
أو يمكنك التعويض في صيغة الجداء الشعاعي للمصفوفات العمودية:
(1, 2, 3)T × (0, 0, 0)T = ( 2×0 - 3×0, 3×0 - 1×0, 1×0 - 2×0)T = 0
طريقة مساعدة لتذكر صيغة الجداء الشعاعي للمصفوفات العمودية
سنوضّح الآن طريقة لحساب الجداء الشعاعي من خلال ترتيب عناصر كل شعاع في محدّد مصفوفة Determinant، والذي يساعدك لتذكر صيغة الجداء الشعاعي السابقة الصعبة جدًا، ولكن إذا كنت تعرف مسبقًا كيفية تقييم المحدّدات ذات الحجم 3x3، فيمكنك تخطي هذه الطريقة، واستخدام الصيغة الموجودة في التعريف.
يحتوي الصف العلوي من المحدّد على الرموز التي تمثل كل محور، ولكن تذكّر أن هذه الطريقة لا تمثّل تعريف الجداء الشعاعي، ولا تمثّل محدد مصفوفة، ولكنها مجرد أداة مساعدة للتذكر.
تعمل هذه الطريقة فقط مع الأشعة ثلاثية الأبعاد، إذ لم يُعرَّف الجداء الشعاعي إلّا للأشعة في الفضاء ثلاثي الأبعاد، لذا ضع مكونات الشعاع الأول في الصف الثاني من المحدّد، ومكونات الشعاع الثاني في الصف الثالث.
تدريب عملي
تدريب1:
لنوجِد الجداء الشعاعي للمصفوفتين العموديتين (1, 2, 1)T و (0, -1, 2)T كما يلي:
ولنقيّم الآن النتيجة من خلال البحث عن العوامل المساعدة للمكوّن i و j و k التي أحطناها بدائرة حمراء في الصف العلوي؛ فالعوامل المساعدة للمكوّن i مثلًا هي عناصر الصفين 2 و 3 التي ليست موجودة في العمود i.
يمكن إيجاد العامل المساعد من خلال ضرب العنصرين الموجودين على القطر الرئيسي، ثم طرح حاصل ضرب العنصرين الموجودين على القطر الآخر من نتيجة ضرب العنصرين الموجودين على القطر الرئيسي، فعلى سبيل المثال، يكون العامل المساعد للمكوّن i هو 2×2 - 1×(-1) = 2 + 1 = 5.
تدريب2:
يكون حاصل الجداء الشعاعي للمصفوفتين العموديتين (0, -1, 2)T و (1, 2, 1)T كما يلي (لاحظ أننا عكسنا ترتيب الشعاعين السابقين):
يتبع تقييم هذا المثال نمط المثال السابق نفسه، ولكن مع تبديل الصفين الثاني والثالث كما يلي:
لاحظ أن النتيجة تمثّل معاكس النتيجة السابقة، مما يدل على أن:
u × v = -(v × u)
ولقد رأينا ذلك سابقًا عندما استخدمنا الأشعة الهندسية.
الجداء الشعاعي لمصفوفة عمودية مع نفسها
يبقى الصفان الثاني والثالث كما هما عندما نأخذ الجداء الشعاع لشعاعٍ مع نفسه، وتذكّر من دروس الرياضيات في المرحلة الثانوية أنه إذا كان صفان من المحدّد متماثلين، فستكون قيمته صفرًا؛ حيث يكون كل عامل مساعد صفرًا، مما يؤدي إلى أن:
0 i + 0 j + 0 k = 0
يحدث الشيء نفسه إذا كان أحد الصفوف مضاعفًا للآخر؛ إذ تعكس هذه النتائج ما رأيناه مسبقًا مع الأشعة الهندسية:
k u × u = 0
تنطبق أيضًا الخاصيات الأخرى لحاصل الجداء الشعاعي للأشعة الهندسية على حاصل الجداء الشعاعي لتمثيلاتها باستخدام المصفوفات العمودية.
وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية حساب الجداء الشعاعي للأشعة، وسنتعرّف في المقال التالي على المصفوفات المستطيلة وعملياتها.
ترجمة -وبتصرُّف- للفصل Vector Cross Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.




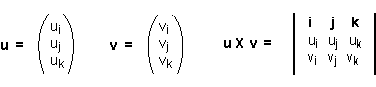
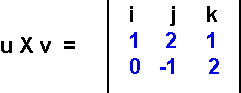
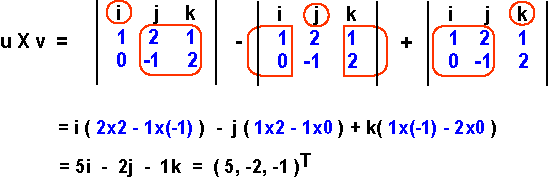
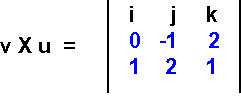
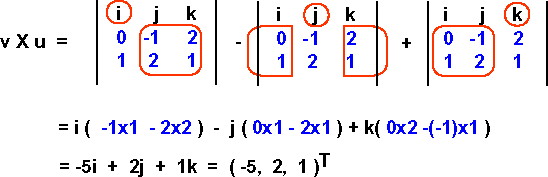











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.