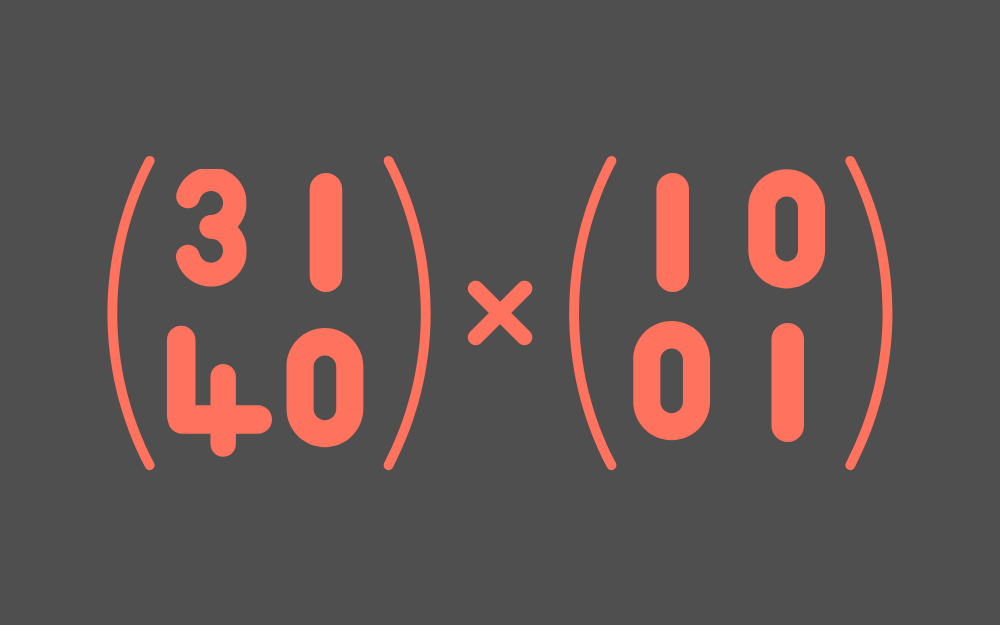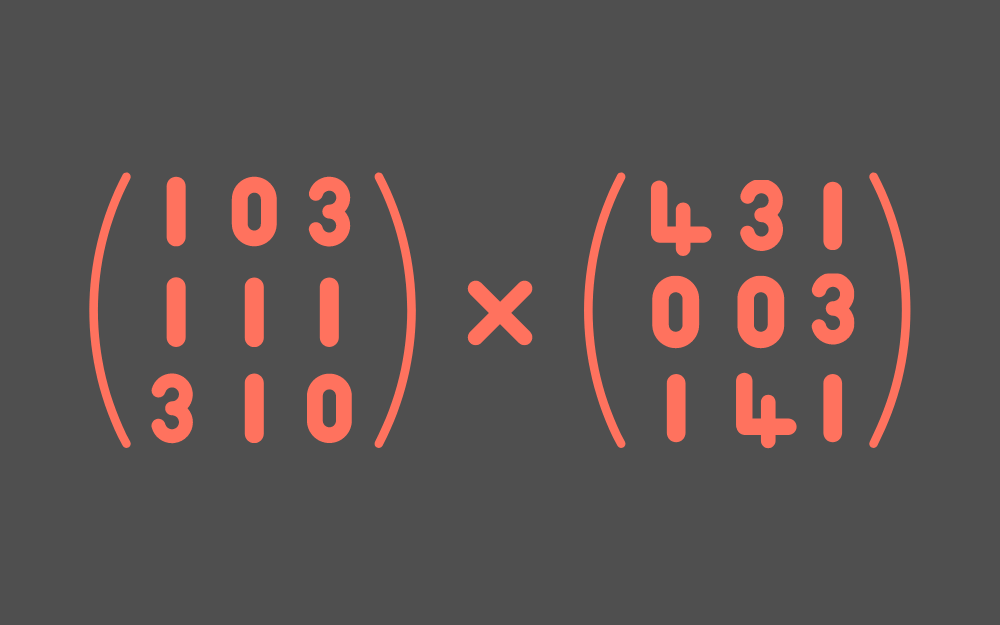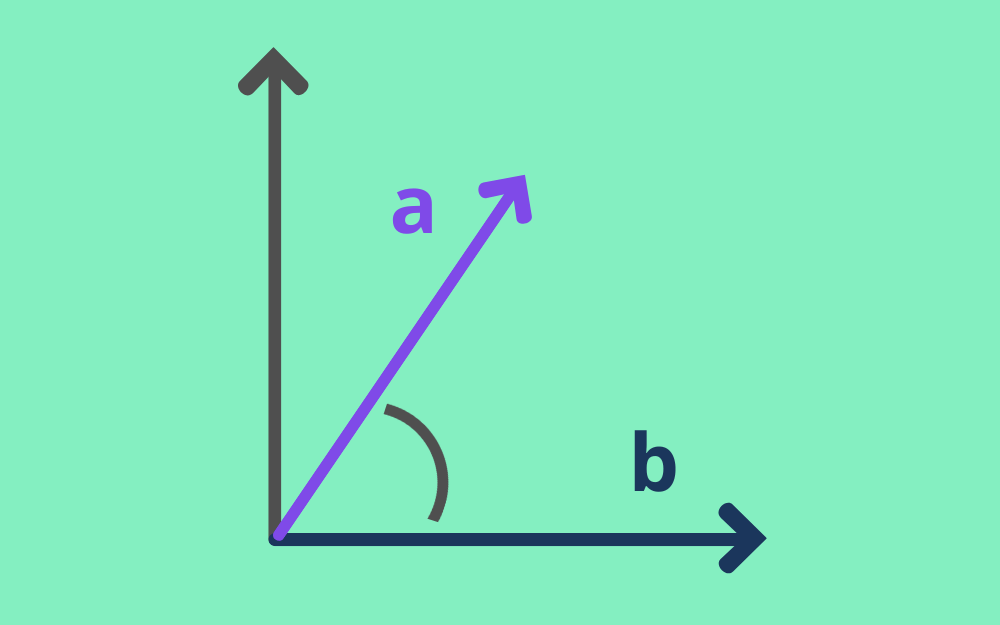البحث في الموقع

لقد تعرفنا في المقالات السابقة على على كيفية ضرب المصفوفات بمصفوفة عمودية وكذلك كيفية حساب عمليات ضرب المصفوفات لعمل تصاميم ثلاثية الأبعاد 3D وغيرها، وسنتابع في هذا المقال، شرح آخر نوع من عمليات ضرب المصفوفات، إذ يوضّح هذا المقال خاصيات أخرى لعملية ضرب المصفوفات، خاصةً المصفوفة المحايدة Identity Matrix ومعكوس المصفوفة Matrix Inverse. سنوضّح في هذا المقال المواضيع التالية: المصفوفة المحايدة: ‎IA = AI = A‎ المصفوفة المحايدة هي مصفوفة فريدة منقول Transpose المصفوفة المحايدة: ‎IT = I‎ ضرب المصفوفة المحايدة بنفسها: ‎II = I‎ المصفوفة المحايدة الموجودة في المنتصف بين مصفوفتين: ‎AIB = AB‎ معكوس مصفوفة: ‎AA-1 = A-1A = I‎ المصفوفات المفردة Singular وغير المفردة Non-singular معكوس المصفوفة هو مصفوفة فريدة معكوس ضرب مصفوفتين: ‎(AB)-1 = B-1 A-1‎‎ معكوس منقول المصفوفة: ‎‎(A-1)T = (AT)-1‎‎ محدِّد Determinant المصفوفة المفردة ستكون جميع المصفوفات في هذا المقال مصفوفات مربعة؛ فالمصفوفة المربعة هي المصفوفة التي يكون فيها عدد الصفوف مساويًا لعدد الأعمدة. الضرب الملحق Post-multiplication للمصفوفات في المصفوفة المحايدة تستخدم الرسوميات الحاسوبية المصفوفات المربعة لأغراض متعددة؛ إذ تُطبَّق معظم عمليات التحويل Transformations، مثل تغيير مجال الرؤية في العالم ثلاثي الأبعاد أو عرضها على صورة ثنائية الأبعاد، باستخدام المصفوفات المربعة. وكما هو معروف، للمصفوفات المربعة خاصيات لا تتشارك فيها مع المصفوفات الأخرى، لذا سنتعرف أولًا على إحدى هذه الخاصيات من خلال إجراء عملية الضرب التالية: وبالتالي نلاحظ أن الضرب الملحق لمصفوفةٍ ما بالمصفوفة المحايدة يعطي المصفوفة نفسها: ‎AI = A‎‎ الضرب المسبق Pre-multiplication للمصفوفات بالمصفوفة المحايدة لنجرِ الآن عملية الضرب التالية: سنلاحظ أن الضرب المسبق لمصفوفةٍ ما بالمصفوفة المحايدة يعطي المصفوفة نفسها: ‎IA = A‎‎ المصفوفة المحايدة Identity Matrix تُسمَّى المصفوفة I بالمصفوفة المحايدة، لأن ضرب المصفوفة بها، يعطي المصفوفة نفسها: IA = A و ‎AI = A‎، وذلك مهما كانت المصفوفة A؛ وهي مشابهة للعدد الحقيقي 1 الذي يمثل العنصر المحايد لعملية ضرب الأعداد الحقيقية، لأن 1a = a و a1 = a لجميع الأعداد الحقيقية a. لا توجد مصفوفة محايدة مُحدَّدة للمصفوفات بجميع أبعادها؛ إذ تكون المصفوفة ‎IN×N‎ مصفوفةًَ محايدةً للمصفوفات المربعة التي أبعادها N×N فقط، فمثلًا المصفوفة المحايدة للمصفوفات التي أبعادها 3×3 هي: نضع العدد 1 مكان عناصر القطر الرئيسي Main Diagonal للمصفوفة المحايدة ذات N بُعد ‎IN×N‎، والعدد 0 للعناصر الأخرى في المصفوفة؛ إذ يتكون القطر الرئيسي من العناصر التي يتساوى فيها رقم الصف مع رقم العمود، ويجب أن تكون الأرقام من النوع 1 على هذا القطر، وليس على القطر الآخر. المصفوفة المحايدة هي مصفوفة فريدة لا توجد مصفوفة أخرى أبعادها N×N تماثل في عملها المصفوفة المحايدة؛ فبما أن العدد 1 فريدٌ بالنسبة للأعداد الحقيقية، فإن المصفوفة المحايدة هي مصفوفةٌ فريدة بالنسبة للمصفوفات التي أبعادها NxN، وسنبرهن ذلك فيما يلي: لنفترض أن جميع المصفوفات لها الأبعاد الصحيحة لعملية الضرب، وأن هناك مصفوفة Z تحقق ما يلي: ‎ZA = A‎ (1)‎ مهما كانت المصفوفة A التي لها الأبعاد الصحيحة، فستعمل المصفوفة Z مثل عمل المصفوفة I، ولكن نأمل أن تكون مختلفةً عنها؛ أما بالنسبة للمصفوفة B فنعلم أن ضرب مصفوفة B بالمصفوفة المحايدة يعطي المصفوفة B نفسها مهما كانت المصفوفة B التي لها الأبعاد الصحيحة. ‎BI = B‎ (2) لنضع المصفوفة المصفوفة I مكان المصفوفة A في العلاقة رقم (1)، بما أن A يمكن أن تكون أي مصفوفة مناسبة. ‎ZI = I‎ (3) ولنضع الآن المصفوفة Z مكان المصفوفة B في العلاقة رقم (2): ZI = Z (4) لاحظ من العلاقتين (3) و(4) أن Z و I متساويين مع الشيء نفسه، لذا يجب أن يكونا متساويين. Z = I (5) يمكنك البدء مرةً أخرى من الخطوة رقم (1) بالترتيب الآخر ‎AZ = A‎ والوصول إلى النتيجة ذاتها؛ لذا إذا وجدت مصفوفةً تعمل مثل عمل المصفوفة المحايدة، فهي بالتأكيد المصفوفة المحايدة بحد ذاتها. خاصيات أخرى للمصفوفة المحايدة لنوضح الآن بعد الخاصيات الأخرى للمصفوفة المحايدة. على سبيل المثال، يُعَد منقول المصفوفة المحايدة هو المصفوفة المحايدة نفسها: IT = I‎ وهناك خاصية أخرى مفيدة للمصفوفة المحايدة، والتي تُعَد مجرد تطبيقٍ لتعريفها؛ حيث إذا جاءت المصفوفة المحايدة بين مصفوفتين، فلن تؤثر على عملية الضرب: AIB = AB‎ كما أن مربع المصفوفة المحايدة هو المصفوفة المحايدة نفسها: I I = I‎ أو I2 = I تُعَد هذه الخاصيات واضحةً ولا حاجة لحفظها. المصفوفة القطرية Diagonal Matrix تُعَد المصفوفة القطرية (a I‎) مفيدةً أحيانًا في الرسوميات الحاسوبية. لنفترض مثلًا أننا نريد حساب الآتي، بحيث يكون a عدد حقيقي و x مصفوفة عمودية: a Ax‎‎‎ هنا وبحالات كثيرة، سنجد أنه من المفيد أحيانًا التفكير على النحو التالي: ‎(a I) Ax وبهذا تكون قد أصبحت جميع العمليات عبارة عن عمليات ضرب مصفوفات، ويُعَد ذلك ميزة، نظرًا لأنه يمكن إجراء عملية ضرب المصفوفات باستخدام عتاد الرسوميات الحاسوبية دون الحاجة لحسابها. لنحاول الآن إيجاد ناتج ضرب المصفوفتين التاليتين بأبسط طريقة كما يلي: عملية ضرب المصفوفات التي ينتج عنها المصفوفة المحايدة من الواضح أن: ‎(2 I)(0.5 I) = 2 (0.5) I = 1 I = I ولكن جرّب ضرب هاتين المصفوفتين بالطريقة العادية: لاحظ أن الصفوف من المصفوفة الأولى تتلاءم مع أعمدة المصفوفة الثانية، بحيث يساوي حاصل الجداء النقطي لها القيمة 1 لعناصر القطر الرئيسي فقط؛ بينما تساوي جميع عمليات الجداء النقطي الأخرى القيمة 0، وبالتالي فالمصفوفة الناتجة هي المصفوفة المحايدة I. معكوس المصفوفة لنفترض أن ax = b للأعداد الحقيقية a و b، وأن المتغير الحقيقي هو x، ولنوجد قيمة x الآن. إذا كان ax = b، فإن ‎(a-1) ax = (a-1)b، أو x = (a-1)b، إلّا عندما يكون العدد a صفرًا؛ فالقيمة (a-1‎) هي معكوس العدد a، وجميع الأعداد الحقيقية غير الصفرية لها معكوس. توجد فكرة مماثلة خاصة بالمصفوفات المربعة، وليكن لدينا مثلًا: Ap = q‎ لدينا: p و q هي أشعة عمودية، أما A فهي مصفوفة أبعادها n×n. ومع افتراض أن A و q معلومتان: لنجرّب معرفة قيمة المصفوفة العمودية p للوصول إلى النتيجة التالية: يُعَد إيجاد قيمة p بالتخمين أمرًا صعبًا، وسيكون الأمر أسوأ بكثير إذا كانت أبعاد المصفوفة A هي 5 × 5؛ لذا توجد طريقة أفضل لذلك، وهي باستخدام معكوس المصفوفة. إذًا، لتكن لدينا p و q مصفوفات عمودية و A مصفوفة أبعادها N×N، حيث تكون قيمة q و A معلومتين، ونريد معرفة قيمة p: ‎q = Ap‎ (1)‎ لنفترض وجود مصفوفة ‎BN×N‎ تحقق ما يلي: ‎p = Bq‎ (2) إذا وُجِدت مثل هذه المصفوفة، فيمكننا حساب ما نريده (أي المصفوفة p) من المصفوفة q، لذا عوّض ما توصلت إليه من العلاقة رقم (2) في العلاقة رقم (1): ‎q = A (Bq)‎ (3) ‎q = (AB) q‎ (4) إذا كانت العلاقة رقم (4) صحيحة، فإن ‎(AB) = I‎. وعلينا هنا أن نتذكّر أن المصفوفة المحايدة هي مصفوفة فريدة. إذا كانت المصفوفة B موجودةً فعلًا، فهي تُعَد معكوسًا للمصفوفة A، وتُكتَب بالشكل: ‎A-1‎؛ وبالتالي يمكننا الآن إيجاد قيمة p في العلاقة رقم (1) من خلال ضرب كل طرف منها في المعكوس ‎ A-1‎كما يلي: A-1 q = A-1 Ap‎ A-1 q = p‎ المصفوفة غير المفردة Non-singular ليس لجميع المصفوفات المربعة معكوس دائمًا، فالمصفوفة الصفرية مثلًا ليس لها معكوس؛ إذ لا توجد مصفوفة ‎0-1‎ تحقق الخاصية: ‎0 ‎0-1‎ = I‎، ولكن الأمر أسوأ من ذلك، فالعديد من المصفوفات المربعة التي أبعادها N × N ليس لها معكوس. تسمى المصفوفة التي لها معكوس: المصفوفة غير المفردة Non-singular، في حسن تسمى المصفوفة التي ليس لها معكوس: المصفوفة المفردة Singular. إذا كانت المصفوفة A غير مفردة، فهي تحقق ما يلي: AA-1= A-1A = I لدينا هنا مثال عن مصفوفة لها معكوس: وليكن لدينا مثلًا ما يلي: بحيث يمكننا إيجاد قيمة p باستخدام المعكوس ‎A-1‎ كما يلي: معكوس المصفوفة هو مصفوفة فريدة إذا كانت المصفوفة A غير مفردة (أي لها معكوس) وكان ‎Ap = q‎، فإن ‎p = A-1 q‎. يُعَد معكوس المصفوفة المربعة غير المفردة فريدًا، وإحدى الطرق لإثبات ذلك هي وجود مصفوفة عمودية واحدة p فقط تُعَد حلًا للمعادلة ‎Ap = q‎، لذلك يجب أن يكون هناك معكوس ‎A-1‎ واحد فقط للمصفوفة. ويُعَد المعكوس ‎A-1‎ مفيدًا في المناقشات حول المصفوفات وعمليات التحويل، ولكنه ليس مفيدًا جدًا للحسابات الفعلية، لذا لا حاجة لحسابه أبدًا. لنفترض مثلًا أن المصفوفة العمودية p تمثل نقطةً في عالم الرسوميات الحاسوبية، وأنه في حال تغير مجال الرؤية، فستُحوَّل المصفوفة العمودية إلى العلاقة ‎ .q = Ap‎ قد يفكر الكثيرون هنا بعكس التحويل باستخدام ‎A-1 q‎، ولكن هناك دائمًا طريقة أسهل للعودة إلى مجال الرؤية الأصلي بدلًا من حساب المعكوس. لنحاول إيجاد ناتج (‎AB) (B-1 A-1‎) كما يلي: باستخدام خاصية التجميع: ‎(‎AB) (B-1 A-1‎) = A (B B-1) A-1 ‎= A I A-1 = A A-1 = I خاصيات معكوس المصفوفة يساوي معكوس ضرب مصفوفتين نتيجة ضرب معكوس المصفوفة الثانية بمعكوس المصفوفة الأولى؛ فقد عكسنا ترتيب المصفوفات كما يلي: ‎(AB)-1 = B-1 A-1 وتوجد خاصية أخرى مفيدة وهي: ‎(A-1)T = (AT)-1 محدد Determinant المصفوفة المفردة يمكن حساب محدِّد المصفوفة التي أبعادها 2 × 2 على النحو التالي: إليك مثال لحساب محدّد مصفوفة: يُعَد حساب محدد المصفوفات الأكبر أكثر تعقيدًا؛ إذ يندر تطبيقها، حيث يُستخدَم المحدّد عند مناقشة المصفوفات، وليس في العمليات الحسابية. ملاحظة: يساوي محدّد المصفوفة المفردة الصفر. رتبة Rank المصفوفة إليك مثال آخر لحساب محدّد مصفوفة: للمصفوفة في المثال السابق محدّد صفري، وبالتالي فهي مصفوفة مفردة، وليس لها معكوس، وتتكون من صفين متطابقين، وبالتالي يمكن القول بأن صفوفها غير مستقلة؛ فإذا كان أحد الصفوف مضاعفًا لصف آخر، فإننا نسمّيها صفوفًا غير مستقلة؛ إذ يساوي محدّد هذه المصفوفة الصفر. وبالمثل، إذا كان أحد الأعمدة مضاعفًا لعمود آخر، فسيكون هذين العمودين غير مستقلين، وبالتالي يكون محدّد هذه المصفوفة صفرًا. رتبة المصفوفة هي الحد الأقصى لعدد الصفوف المستقلة (أو الحد الأقصى لعدد الأعمدة المستقلة)، وتكون المصفوفة المربعة ‎An×n‎ غير مفردة فقط إذا كانت رتبتها تساوي n. لنجرب إيجاد رتبة المصفوفة التالية: رتبة المصفوفة السابقة هي 3، حيث يُعَد الصف الأخير مضاعفًا للصف الأول. خاتمة بهذا نكون قد تعرفنا على مفهوم كل من المصفوفة المحايدة Identity Matrix ومعكوس المصفوفة وكيفية استخدامهما في عملية ضرب المصفوفات. وبهذا نكون قد وصلنا لنهاية هذه السلسلة التعليمية حول الأشعة وجبر المصفوفات من وجهة نظر رسومات الحاسوب، حيث غطينا عدة مواضيع عن الأشعة والمصفوفات وتعرفنا على عدة حالات للتعامل معها. ترجمة -وبتصرُّف- للفصل Identity Matrix and Matrix Inverse من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: ضرب المصفوفات وحسابها لعمل تصاميم ثلاثية الأبعاد 3D التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد تعرف على المصفوفات Matrices وعملياتها البسيطة في التصاميم 3D

تُستخدَم عملية ضرب المصفوفات في الرسومات الحاسوبية من أجل إنشاء مصفوفات التحويل Transformation التي تُطبَّق على النقاط والأشعة. وتُصمَّم المناظر في الألعاب ذات نمط منظور الشخص الأول First Person Game مثل لعبة DOOM باستخدام النقاط والأشعة أيضًا، كما ينشأ العرض المتغير الذي نراه أثناء تحرّك اللاعب عبر هذه المناظر بتحويل تلك النقاط والأشعة. ونظرًا لأهمية المصفوفات في مجال النقاط والأشعة التي بدورها تتداخل مباشرةً مع عملية إنشاء تصاميم ثلاثية الأبعاد، فسنفصل في هذا المقال في كيفية التعامل مع المصفوفات وضربها ببعضها. لقد تحدثنا في المقال السابق عن كيفية ضرب المصفوفات بمصفوفة عمودية، ولمعرفة كيفية التعامل مع المصفوفات أكثر، سنناقش بهذا المقال مفهوم ضرب المصفوفات وخاصيتها وكيفية حسابها لعمل تصاميم ثلاثية الأبعاد 3D؛ وسنتحدث عما يلي: متى نضرب المصفوفات ناتج ضرب المصفوفات نتاج كل عنصر من عناصر المصفوفة المحصل عليها بتطبيق عملية جداء نقطي الخاصية التجميعية لضرب المصفوفات الخاصية غير التبديلية لضرب المصفوفات توزيع ضرب المصفوفات على عملية الجمع الضرب بالمصفوفة الصفرية أبعاد نتيجة ضرب المصفوفات يمكن ضرب المصفوفتين ‎A4×3‎ و ‎B3×5‎ عند تطابق البعد الداخلي الذي قيمته 3؛ فإذا رتبنا مصفوفتين مستطيلتين بحيث يكون البعد الداخلي لكل منهما متساويًا، فيمكن ضرب هاتين المصفوفتين، وستكون النتيجة عمومًا عبارة عن مصفوفة مستطيلة كالآتي: AR×N‎ BN×C‎ = ZR×C‎ تحتوي عملية الضرب AB -إذا كان تشكيلها ممكنًا- على نفس عدد صفوف المصفوفة A وعلى نفس عدد أعمدة المصفوفة B؛ وهنا إذا لم نتمكن من تجاهل البعد الداخلي، فلن نتمكن من تشكيل عملية الضرب. فلنطّلع الآن على المثال التالي، مع تجاهل كيفية حساب العناصر مبدئيًا؛ إذ سنضرب مصفوفةً أبعادها 3‎×2 في مصفوفة أخرى أبعادها 2‎×2، والنتيجة ستكون عبارة عن مصفوفة أبعادها 3‎×2: انطلاقًا مما سبق، نستطيع القول أن أبعاد نتيجة ضرب المصفوفتين ‎A4×4‎ B4×2‎ مثلًا، ستكون: A4×4‎ B4×2‎ = C4×2 ملاحظة: تُعَد المصفوفات العمودية والمصفوفات السطرية حالة خاصة من المصفوفات المستطيلة، لذا فإن قاعدة أبعاد نتيجة ضرب المصفوفات تسري عليها أيضًا. لنتدرب الآن على مزيدٍ من الأمثلة في الجدول التالي؛ إذ سنحدّد أبعاد نتيجة ضرب كلّ زوج من المصفوفات: أبعاد المصفوفة الأولى أبعاد المصفوفة الثانية النتيجة 4‎ × 3 ‫ 3‎ × 2 ‫ 4‎ x 2 2‎ × 3 ‫ 2‎ × 3 ‫ غير ممكنة 3‎ × 5 ‫ 5‎ × 1 ‫ 3‎ x 1 3‎ × 2 ‫ 2‎ × 2 ‫ 3‎ x 2 4‎ × 3 ‫ 3‎ × 1 ‫ 4‎ x 1 3‎ × 1 ‫ 1‎ × 4 ‫ 3‎ x 4 ملاحظة: سنحتاج للتحقق دائمًا من أبعاد نتيجة ضرب المصفوفات قبل إجراء العمليات الحسابية؛ فمثلًا، عملية الضرب الأخيرة في الجدول السابق غريبة بعض الشيء، ومن السهل أن يختلط علينا الأمر دون معرفة الشكل الذي يجب أن تبدو عليه النتيجة. يمكننا تشكيل عملية الضرب ‎An×m‎ Bm×p‎، ولكن لا يمكننا تشكيل عملية الضرب ‎Bm×p‎ An×m‎ إذا كانت n ≠ p. وسيتضح لاحقًا أنه حتى لو أمكن تشكيل كلتا عمليتي الضرب، فمن النادر أن يكون ‎AB = BA‎. تشكيل عملية ضرب المصفوفات يُحسَب حاصل ضرب مصفوفتين AB من خلال تطبيق الجداء النقطي على كل صف من المصفوفة A مع كل عمود من المصفوفة B، بحيث يكون عدد الأعمدة في المصفوفة A مساويًا لعدد الصفوف في المصفوفة B. لنجرب قلب أحد أعمدة المصفوفة B بحيث تصبح عناصره محاذيةً لصفوف المصفوفة A، ثم نطبّق عليها الجداء النقطي؛ وهنا سينتج لدينا العنصر الموجود في الصف 1 والعمود 1 من المصفوفة الناتجة. لننتقل بعدها إلى الصف التالي مع تطبيق الجداء النقطي، لينتج لدينا العنصر الموجود في الصف 2 والعمود 1 من المصفوفة الناتجة؛ وسنستمر بهذه العملية حتى الوصول إلى الصف الأخير. لننتقل الآن إلى العمود التالي ونقوم بنفس الشيء عند الانتهاء من العمود الأول من المصفوفة B، ونواصل تطبيق ذات الشيء على كل عمود من المصفوفة B حتى حساب جميع العناصر. ملاحظة: العنصر ij من المصفوفة الناتجة = الجداء النقطي للصف i من المصفوفة A مع العمود j من المصفوفة B. لنفترض أننا نشكّل عملية الضرب التالية: ‎A5×3‎ B3×2 = C5×2 سنستخدم الصف الثالث من المصفوفة A والعمود الثاني من المصفوفة B، لحساب الصف الثالث، والعمود الثاني من المصفوفة الناتجة C. طريقة أخرى لتصور عملية ضرب المصفوفات قد تعرض كتب الرسوميات الحاسوبية طريقةً مختلفةً لضرب المصفوفات؛ إذ أن هناك عدة طرق للتفكير في الأمر بالرغم من أن النتائج هي نفسها. يوضّح الرسم البياني التالي مثلًا طريقةً أخرى لتصور عملية الضرب ‎AB = C‎؛ إذ سنكتب المصفوفة A على يسار المصفوفة الناتجة C والمصفوفة B فوقها، ثم نرسم خطوطًا أفقية وأخرى عمودية لتقسيم المصفوفة C إلى خلايا؛ وسيؤدي ذلك تلقائيًا إلى تشكيل العدد الصحيح من الخلايا. ينتج العدد الذي يجب وضعه في كل خلية من حاصل الجداء النقطي لصف المصفوفة A مع عمود المصفوفة B اللذين يتقاطعان عند هذه الخلية. لنحسب الآن قيمة العنصرين c11‎ و c32‎ كما يلي: c11 = 1×4 + -2×-1 = 6 c32 = -1×1 + 4×2 = 7 سنجرّب الآن حساب حاصل الجداء النقطي الخاص بكل خلية في الرسم البياني التالي: وستكون المصفوفة الناتجة هي المصفوفة التالية: عناصر المصفوفة هي أعداد حقيقية يُعَد كل عنصر في المصفوفة مقدارًا سلميًا Scalar أي عددًا حقيقيًا. لقد استخدمنا في أمثلتنا السابقة أعدادًا صحيحة حتى تكون العملية الحسابية سهلة، ولكن إليك مثال آخر مع قيم عشرية: تشتمل معظم برامج جداول البيانات والآلات الحاسبة الإلكترونية العلمية على دالات رياضية خاصة بالمصفوفات؛ لكن من الأفضل محاولة إجراء الحسابات ذاتيًا عند التعلم من أجل استيعاب العملية. عملية ضرب المصفوفات ليست عملية تبديلية لا تُعَد المساواة ‎AB= BA‎ صحيحةً دائمًا، فحتى إذا تمكنا من تشكيل هاتين العمليتين، فمن النادر أن تكون نتيجتهما متساويتين. لنحسب مثلًا عمليتي الضرب التاليتين: العملية النتيجة الناتج الناتج وهذا يوضّح أن ‎ AB ≠ BA‎بصورة عامة بالنسبة للمصفوفتين A و B، ولكن يمكن مثلًا: A4×4 04×4 = 04×4 A4×4 = 04×4 المصفوفة 0 هي المصفوفة الصفرية ذات الأبعاد الصحيحة لجعل عملية الضرب ممكنة، وبالتالي يمكن أن تكون عملية الضرب عمليةً تبديليةً ‎AB = BA‎ بالنسبة لبعض المصفوفات؛ ولكن لا يمكننا تعميم هذه الخاصية على جميع المصفوفات. تدريب عملي لنوجد ناتج ضرب المصفوفتين التاليتين: لنجرب أيضًا ضرب المصفوفتين التاليتين مثلًا: استخراج عامل عددي من مصفوفة ليكن c(AB) = (cA)B‎ من أجل العدد الحقيقي c، علمًا أن أن c A‎ يعني أن كل عنصر من عناصر المصفوفة A مضروب بالعدد c. سنوضّح هذه القاعدة في المثال التالي: يمكننا تبسيط عملية ضرب المصفوفات في كثير من الأحيان من خلال استخراج عامل عددي من إحدى المصفوفات كما في المثال التالي: عملية ضرب المصفوفات هي عملية تجميعية لنضرب المصفوفتين الأوليتين، ثم نضرب النتيجة بالمصفوفة الثالثة كما يلي: ولنبدأ الآن بالمصفوفتين الأخيرتين أولًا كما يلي: وكما هو واضح، الإجابة النهائية هي نفسها بكلا الطريقتين، وهذا يوضّح أن عملية ضرب المصفوفات هي عملية تجميعية Associative: (AB) ‪C = A (BC) يجب أن تكون الأبعاد الداخلية للمصفوفتين A و B نفسها، كما يجب أن تكون الأبعاد الداخلية للمصفوفتين B و C نفسها. تُكتَب عملية ضرب ثلاث مصفوفات في العادة بالشكل الآتي: ABC. إذًا لنفترض مثلًا: A5×5 B?×? C3×4 = D?×?‪ حيث تكون أبعاد المصفوفتين B و D كما يلي: ‪A5×5 B5×3 C3×4 = D5×4 خاصية توزيع ضرب المصفوفات في جمعها تتعامل خاصية التوزيع مع تعبيرٍ يحتوي على كلٍّ من عمليتي ضرب وجمع المصفوفات؛ وسنتبع الخطوات التالية لذلك. أولًا، نجمع المصفوفتين كما يلي: ثانيًا، نضرب المصفوفتين: ثالثًا، نجري العملية مرةً أخرى بترتيب مختلف؛ إذ سنجري أولًا عملية ضرب المصفوفة اليسرى بكل من المصفوفتين الأخريين كما يلي: في الأخير، نجمع ناتج عمليتي الضرب السابقتين: وكما نلاحظ، كلتا النتيجتين متماثلتان، مما يدل على أن ضرب المصفوفات توزيعيٌّ على جمعها: ‪A (B + C) = AB + AC ويمكن القول أيضًا أن: (X + Y) Z = XZ + YZ ملاحظة: استخدمنا في معظم أمثلتنا أعدادًا صحيحة، ولكن لا يجب أن ننسى أن عناصر المصفوفة قد تكون أعددًا حقيقية أو متغيرات كما يلي: ملخص بالقواعد الخاصة بعملية ضرب المصفوفات سنذكر الآن قائمة بالقواعد الخاصة بعملية ضرب المصفوفات التي ناقشناها في هذا المقال، حيث تفترض كل قاعدة أنه يمكن ضرب المصفوفات؛ أي أن أبعادها مناسبة لعملية الضرب: يمكن تشكيل عملية ضرب المصفوفات في حال: إذا كان ‎AM×K BK×N = C‎، فإن C = CM×N‎ ضرب المصفوفات ليس عملية تبديلية: ‎AB ≠ BA‎، إلّا في حالات ناردة ضرب المصفوفات هو عملية تجميعية: A (BC) = (AB) C = ABC استخراج المعامل العددي من المصفوفات: a(AB) = (a A) B = a AB = A (a B) خاصية التوزيع على الجمع: A ( B + C) = AB + AC (A + B) C = AC + BC الضرب بالمصفوفة الصفرية 0: 0A = 0 بهذا نكون قد وصلنا إلى نهاية هذا المقال التي تعرّفنا من خلاله على عملية ضرب المصفوفات وحسابها، وسنناقش في المقال التالي مزيدًا من خاصيات عملية ضرب المصفوفة بمصفوفة أخرى. ترجمة -وبتصرُّف- للفصل Matrix-Matrix Multiplication من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: ضرب المصفوفات بمصفوفة عمودية في التصاميم ثلاثية الأبعاد 3D التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد تعرف على المصفوفات Matrices وعملياتها البسيطة في التصاميم 3D

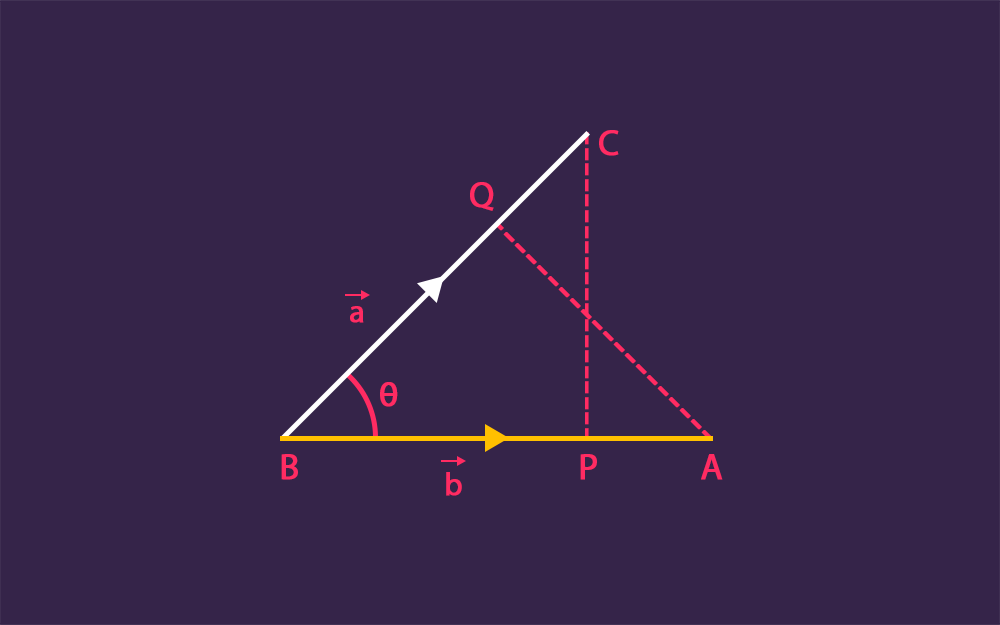
ناقشنا في مقالٍ سابق أن الرسوميات الحاسوبية ثلاثية الأبعاد تتكون من عمليتين: أولهما إنشاء عالم خيالي داخل الحاسوب، وثانيهما إنتاج صور ثنائية الأبعاد لذلك العالم من مجالات رؤية مختلفة؛ إذ يُعَد إنتاج صورة ثنائية الأبعاد من صورة ثلاثية الأبعاد مثالًا عن عملية الإسقاط Projection، وسنناقش في هذا المقال المفاهيم الأساسية فقط للإسقاط. سنوضّح في هذا المقال المواضيع التالية: تشكيل مستوٍ Plane واحد من شعاعين. مفهوم الإسقاط. إسقاط شعاعٍ على شعاع آخر. صيغة لإسقاط الأشعة. طريقة إسقاط الأشعة خطوةً بخطوة. المكون العمودي لإسقاط الأشعة. مثال لإسقاط الأشعة ثنائية الأبعاد. مثال لإسقاط الأشعة ثلاثية الأبعاد. المساقط ثنائية الأبعاد المتعددة يمكن إنتاج عدد لا نهائي من الصور ثنائية الأبعاد من نموذج واحد ثلاثي الأبعاد، فمثلًا، يعرض الشكل التالي إسقاط نموذج ثلاثي الأبعاد لصندوق على عرضٍ ثنائي الأبعاد؛ إذ تنتِج المواقع المختلفة لمجال الرؤية صورًا مختلفة ثنائية الأبعاد، وتُسقَط الأشعة ثلاثية الأبعاد للنموذج على سطح العرض لتكوين أشعة الصورة ثنائية الأبعاد. تشكيل مستوٍ واحد من شعاعين يمكن تشكيل مستوٍ واحد باستخدام شعاعين ونقطة دائمًا، إلا في حال كان هذان الشعاعان متوازيان. لا بد أنك تتذكر من مادة الهندسة في المرحلة الثانوية أن الخطين غير المتوازيين (ليسا على استقامة واحدة) يحددان مستوٍ واحد، وبالتالي ينطبق الشيء نفسه على الأشعة. تبدأ معظم الأمثلة في هذا المقال بشعاعين ثنائي الأبعاد، ولكن ستكون النتائج صالحة لشعاعين ثلاثي الأبعاد؛ إذ يحدّد شعاعان ثلاثي الأبعاد مستوٍ واحد أيضًا. يوضّح الشكل السابق الشعاع w والشعاع v، وجعلنا ذيل هذين الشعاعين يبدأ من النقطة نفسها لتسهيل التصور، ولكن لا تنسَ أن الأشعة ليس لها موضع محدّد، وجعلنا الشعاع v أفقيًا للسهولة أيضًا، ولكن يمكن أن يكون له أيّ منحى Orientation. إسقاط شعاع على شعاع آخر إذا ضربنا الشعاع v بعدد حقيقي Scalar (أو مقدار سلمي) k، فسيؤدي ذلك إلى تغيير طول هذا الشعاع، ولكنه لن يؤثر على منحاه، وبالتالي ليكن لدينا الشعاعان w و v كما في الشكل التالي: يمكن أن يكون الشعاعان w و v أيّ شعاعين، ونريد شعاعًا u عموديًا على الشعاع v وعددًا حقيقيًا k مضروبًا به، بحيث: w =‎ k v + u‎ ويسمى عندها k v‎ مسقط الشعاع w على الشعاع v. صيغة لكيفية إسقاط الأشعة ملاحظة: إذا كان الشعاعان u و v متعامدان، فإن الجداء النقطي لهما هو: ‎.u · v = 0 يجب أن تتحقق العلاقة: k v + u = w‎ بشرط أن يكون u عموديًا مع v، حتى يكون k v‎ مسقط الشعاع w على الشعاع v؛ إذ نعلم من علم المثلثات أن: طول المسقط k v‎ =‫ ‎| w | cos θ. منحى k v‎ هو شعاع الوحدة ‎vu‎. تذكر أن أشعة الوحدة Unit Vectors تُستخدَم لتمثيل المنحى في الفضاء ثلاثي الأبعاد، وبالتالي يكون منحى الشعاع v هو شعاع الوحدة ‎vu‎؛ إذ يبدو المنحى أفقيًا في الشكل السابق، ولكننا استخدمنا ذلك للسهولة فقط. وبما أن cos θ يساوي ‎wu · vu‎، فسينتج ما يلي: ‎k v = | w | (wu · vu) vu يمثل الجزء ‎| w | (wu · vu)‎ عددًا حقيقيًا بحيث يُضبَط الشعاع v على الطول المطلوب، وهو طول الخط الأفقي باللون الأزرق الفاتح في الشكل السابق؛ بينما يعبّر الجزء المتبقي من الصيغة: ‎vu‎ عن منحى الشعاع v نفسه. طريقة إسقاط الأشعة خطوة بخطوة تذكير: يمكنك حساب شعاع الوحدة من خلال تقسيم الشعاع على طوله. لنتّبع طريقة خطوة بخطوة لإسقاط الشعاع w على v، بدلًا من حفظ الصيغة السابقة لتطبيق عملية الإسقاط. أولًا، نحسب أطوال الأشعة كما يلي: ‎| w | = √(w · w) ‎| v | = √(v · v) ثانيًا، نحسب أشعة الوحدة: wu = w / | w‎ |‎ vu = | v | / | v |‎ ثالثًا، نحسب جيب تمام Cosine الزاوية بين الشعاعين: wu · vu رابعًا، نعوّض في صيغة الإسقاط التالية: ‎k v = | w | (wu · vu) vu المكون العمودي لإسقاط الأشعة ملاحظة: لا يُعَد مسقط الشعاع w على الشعاع v مماثلًا لمسقط الشعاع v على الشعاع w، إذ يكون منحى الشعاع الناتج عن عملية الإسقاط بالاتجاه نفسه للشعاع المُسقَط عليه. أوجدنا في الفقرة السابقة k v‎، لذا من السهل العثور على الشعاع المتعامد معه u: ‎w = k v + u‎، إذًا ‎u‎ = w - k v‎ تعبّر إشارة "+" في الصيغة السابقة عن جمع الأشعة، وتعبّر إشارة "-" عن طرح الأشعة. تدريبات عملية كانت الأشعة في هذا المقال جميعها أشعةً هندسيةً حتى الآن، إذ لم يكن هناك أيّ ذكرٍ للإطارات الإحداثية أو المصفوفات العمودية، ولكن ستنجح هذه النتائج عند تمثيل الأشعة بالمصفوفات العمودية كما سنرى في الأمثلة التالية. تدريب 1: نمثّل الشعاع w بالمصفوفة العمودية ‎(6, 5)T‎، ونمثّل الشعاع v بالمصفوفة العمودية ‎(9,0)T‎، ولنوجد مسقط الشعاع w على الشعاع v، أي لنبحث عن الشعاعين k v‎ و u. يمكنك ببساطة قراءة الإجابة من الرسم البياني الورقي التالي، ولكن تظاهر أنك لم تلاحظ ذلك. أولًا، نحسب الأطوال كما يلي: ‎| w | = √ ((6, 5)T‎·(6, 5)T‎) = 7.81‎ ‎| ‎v | = √ ((9, 0)T‎·(9, 0)T‎) = 9 ثانيًا، نحسب أشعة الوحدة كما يلي: ‎wu = (6, 5)T / 7.81 ‎vu = (9, 0)T / 9 = (1, 0)T ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين وهو: ‎wu · vu = (1/7.81) (6, 5)(1, 0)T · (1, 0)(1, 0)T = 6/7.81 رابعًا، نعوّض في صيغة الإسقاط التالية: k v = | w | (wu · vu) vu ‎‎k v = 7.81 (6/7.81) (1, 0)T = 6(1, 0)T = (6, 0)T خامسًا، نحسب الشعاع العمودي: u = w - k v ‎u = (6, 5)T - (6, 0)T = (0, 5)T والنتيجة هي أن ‎u = (6,0)T + (0,5)T‎ كما هو متوقع. وكان هذا المثال سهلًا طبعًا. ملاحظة: ليس عليك أن تحسب طول w، لأنه يُلغَى قبل الإجابة النهائية، لذا فكل ما تحتاج إليه هو مربع طول v، أي ‎|v|2‎؛ إذ تعرض بعض الكتب صيغًا مختلفة للإسقاط تستفيد من هذه الحقائق. تدريب 2 إليك مثال آخر، ولكنه ليس بهذه السهولة، إذ نمثّل الشعاع w هنا بالمصفوفة العمودية ‎(3.2, 7)T‎، ونمثّل الشعاع v بالمصفوفة العمودية ‎(8, 4)T‎؛ ولنوجِد الآن الشعاعين k v‎ و u. أولًا، نحسب الأطوال كما يلي: | w | = (لا داعي لحسابه، لذا أبقيه بالرموز) ‎| v |2 = (8, 4)T ·(8, 4)T = 80 ثانيًا، نحسب أشعة الوحدة وهي: wu = (3.2, 7)T / | w |‎ vu = (8, 4)T / | v |‎ ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي: ‎wu · vu = (3.2, 7)T / | w | · (8, 4)T / | v | = 53.6 /( | w | | v |)‎ رابعًا، نعوّض في صيغة الإسقاط التالية: ‎k v = | w | (wu · vu) vu k v = | w | [53.6 / (| w | | v |)] (8, 4)T / | v |‎ k v = 53.6 / (| v |) (8, 4)T / | v |‎ ‎k v = 53.6 / (| v |2) (8, 4)T ‎k v = 53.6 / 80 (8, 4)T k v = ((53.6*8)/80, (53.6*4)/80)T = ( 5.3, 2.68)T خامسًا، نحسب الشعاع العمودي: u = w - k v u = (3.2, 7)T - (5.3, 2.68)T = (-2.1, 4.32)T لنتحقّق الآن من أن: ‎w = k v + u‎ من خلال تعويض النتائج في العلاقة k v + u‎ كما يلي: ‎( 5.3, 2.68)‎T + (-2.1, 4.32)T = (3.2, 7.0)T = w فوائد عملية إسقاط الأشعة يجب أن تفهم جيدًا ما يحدث عند إسقاط شعاع على شعاع آخر، إذ تحدث عملية الإسقاط -كما ذكرنا سابقًا- باستمرار عندما يعرض الحاسوب الرسوميات. تُنفَّذ معظم العمليات الحسابية في عتاد الرسوميات الخاصة بالحاسوب، ويجري إسقاط ملايين الأشعة في الثانية الواحدة؛ فإذا أردتَ أن تعرف ما يحدث في الرسوميات الحاسوبية، فيجب أن تعرف ما هي عملية الإسقاط. لنوجِد الآن مسقط الشعاع w على الشعاع v في الرسم البياني التالي: حاول إجراء العمليات الحسابية المطلوبة كما فعلنا في الأمثلة السابقة، ولكن يمكن أن تحصل على الإجابات التالية مباشرةً من قراءة الرسم البياني السابق: w = (4, 8.2)T v = (2.8, 1.75)T k v = (5.8, 1.6)T u = (-1.8, 6.4)T تبدو الإجابات السابقة جيدة، ولكن لنتحقّق منها كما يلي: أولًا، هل ‎w = k v + u‎؟ ‎(5.8, 1.6)T + (-1.8, 6.4)T = (4, 8.0)T = w (حسنًا، تقريبًا) ثانيًا، هل ‎v · u = 0.0؟ ‎(5.8, 1.6)T · (-1.8, 6.4)T = -10.44 + 10.24 = -0.2 = ‎0.0‎ (تقريبًا)‎ ملاحظة: لنفكر في جميع الأشعة المحتملة w و v ومسقط الشعاع w على الشعاع v، إذ يمكن أن يكون الشعاع k v‎ أطول من الشعاع v كما في المثال السابق، ولكن لا يمكن أن يكون الشعاع k v‎ أطول من الشعاع w، فأكبر طول ممكن للشعاع k v‎ هو | w | عندما يكون w و v على استقامة واحدة. مثال آخر لعملية الإسقاط لاحظ أن عملية إسقاط الشعاع w على v لا تعتمد على طول v، بل يؤثر اتجاه الشعاع v فقط على النتائج. يكون طول المسقط هو ‎| w | cos θ، حيث θ هي الزاوية بين الشعاعين، وبما أن دالة جيب التمام لا تزيد عن 1 أبدًا، فلن يكون طول المسقط أبدًا أطول من الشعاع المُسقَط. أسقِط الشعاع w على الشعاع v من خلال الاطلاع على الرسم البياني التالي: وستحصل على الإجابات التالية: w = (-5, 5)T v = (5, 1)T k v = (-3.8, -.8)T u = (-1.3, 5.6)T حصلنا على الإجابات السابقة من خلال قراءة الرسم البياني السابق، ولكنها ليست دقيقة بالضرورة، إذًا لنتحقّق منها. أولًا، هل ‎w = k v + u‎؟ ‎(-3.8, -0.8)T + (-1.3, 5.6)T = (-5.1, 4.8)T = w (تقريبًا) ثانيًا، هل ‎v · u = 0.0؟ ‎‎(5, 1)T · (-1.3, 5.6)T = -6.5 + 5.6 = -0.9 = 0.0 (ليس تمامًا) ملاحظة: يمكن لمسقط الشعاع w على الشعاع v أن يؤشّر إلى الاتجاه المعاكس للشعاع v كما حدث في المثال السابق. أمثلة لإسقاط الأشعة ثلاثية الأبعاد سنستعرض هنا بعض الأمثلة حول كيفية إسقاط الأشعة ثلاثية الأبعاد المثال الأول يظهر الرسم البياني السابق الشعاعين التاليين: ‎w = (4, 2.5, 2.5)T‎ (الشعاع الأحمر) ‎v = (5, 0, 3.1)T (الشعاع الأخضر) أسقِط الشعاع w على الشعاع v، وتذكّر أن طول الشعاع v لا يؤثر على الإسقاط، بل يؤثر منحاه عليه فقط، لذا أنزِل رأس سهم الشعاع w على الخط المنقط. يمكن بالنظر تقدير مسقط الشعاع ‎w = (4, 2.5, 2.5)T‎ على الشعاع ‎v = (5, 0, 3.1)T‎ بأنه k v = (4, 0, 2.5)T‎. يتضمن إسقاط الشعاع w على الشعاع v في هذه الحالة "انهيار Collapsing" البعد y للشعاع w. فلنتحقّق الآن مما إذا كانت النتيجة نفسها رياضيًا، إذ يمكن تطبيق الخطوات نفسها في الفضاء ثلاثي الأبعاد 3D. أولًا، نحسب الأطوال وهي: | w | = (لا داعي لحسابه، لذا أبقيه بالرموز) ‎| v |2 = ((5, 0, 3.1)T · (5, 0, 3.1)T) = 34.61 ثانيًا، نحسب أشعة الوحدة كما يلي: wu = (4, 2.5, 2.5)T / | w |‎ vu = (5, 0, 3.1)T / | v |‎ ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي: ‎wu · vu = (4, 2.5, 2.5)T / | w | · (5, 0, 3.1)T / | v | = 27.75 / ( | w | | v |) رابعًا، نعوّض في صيغة الإسقاط التالية: ‎k v = | w | (wu · vu) vu‎ k v = | w | (27.75 / (| w | | v |)) (5, 0, 3.1)T / | v |‎ k v = 27.75 / (| v |) (5, 0, 3.1)T / | v |‎ ‎k v = 27.75 / (| v |2) (5, 0, 3.1)T k v = (27.75 / 34.61) (5, 0, 3.1)T‎ ‎k v = ((27.75*5)/34.61, 0, (27.75*3.1)/34.61)T ‎k v = ( 4.00, 0, 2.49)T وبالتالي فإن التقدير بالنظر k v = (4, 0, 2.5)T‎ يطابق النتيجة الرياضية ‎(4, 0, 2.5)T‎، ويمكن الآن بسهولة حساب الشعاع العمودي: u = w - k v u = (4, 2.5, 2.5)T - (4, 0, 2.5)T = (0, 2.5, 0)T أبقِ الشعاع w كما هو في الرسم البياني السابق، وحاول تصوّر إسقاط w على شعاع مختلف v'‎ ينتج عنه المسقط k ،v'‎ الذي يؤدي إلى انهيار البعدين y و z للشعاع w؛ فمثلًا، إذا أسقطنا الشعاع ‎w = (4, 2.5, 2.5)T‎ على الشعاع ‎v' = (1, 0, 0)T‎، فستكون النتيجة k v = (4, 0, 0)T‎. المثال الثاني إذا أسقطنا شعاعًا في فضاء ثلاثي الأبعاد على محاور إحداثية، فستحصل على أحد الأبعاد الثلاثة فقط لذلك الشعاع، لذا لنلقِ نظرة على مثال آخر أصعب. لدينا من الشكل السابق الشعاعان ‎w = (4, 2, 3)T‎ و ‎v = (6, 4, 2)T‎، ونريد إسقاط الشعاع w على الشعاع v. يمكن أن نقدّر بالنظر أنه إذا "أنزلنا" رأس سهم الشعاع w عموديًا على الشعاع v، فستصل إلى الشعاع v عند حوالي 4/10 من طول v، لذا فإن k تساوي 0.4 تقريبًا و k v‎ يساوي: k v = 0.4 (6, 4, 2)T = (2.4, 1.6, 0.8)T ولكن سيتضح معنا أن هذه النتيجة التقديرية خاطئة بصورة فادحة، إذ يُعَد إيجاد الحل بالنظر في المسائل ثلاثية الأبعاد أمرًا صعبًا، إلّا إذا كانت لديك صورة ثلاثية الأبعاد فعلية أمامك. على هذا الأساس، دعنا نتحقق من الإجابة رياضيًا. أولًا، نحسب الأطوال وهي: | w | = (لا داعي لحسابه، لذا أبقيه بالرموز) ‎| v |2 = ((6, 4, 2)T · (6, 4, 2)T) = 56 ثانيًا، نحسب أشعة الوحدة كما يلي: wu = (4, 2, 3)T / | w |‎ vu = (6, 4, 2)T / | v |‎ ثالثًا، نحسب جيب تمام الزاوية بين الشعاعين كما يلي: wu · vu = (4, 2, 3)T · (6, 4, 2)T / | w | | v | = 38 / ( | w | | v |) رابعًا، نعوّض في صيغة الإسقاط التالية: k v = | w | (wu · vu) vu k v = | w | {38 / (| w | | v |)} {(6, 4, 2)T / | v |} k v = {38 / | v |} {(6, 4, 2)T / | v |} k v = {38 / | v |2} (6, 4, 2)T k v = {38/56} (6, 4, 2)T k v = 0.679 (6, 4, 2)T k v = ( 4.07, 2.7, 1.36)T لنحسب الآن الشعاع u كما يلي، حيث ‎u + k v = w‎ (الشعاع u هو الشعاع الأسود المنقط في الرسم البياني السابق): u + k v = w u = w - k v = (4, 2, 3)T - ( 4.07, 2.7, 1.36)T = (-0.07, -0.7, 1.64)T بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية إسقاط شعاع على شعاع آخر في فضاء ثنائي وثلاثي الأبعاد، وسنتعرّف في المقال التالي على عملية الجداء الشعاعي للأشعة. ترجمة -وبتصرُّف- للفصل Projecting one Vector onto Another من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: كيفية إيجاد الزاوية بين شعاعين في فضاء ثلاثي الأبعاد 3D تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D تطبيق الجداء النقطي Dot Product على الأشعة في التصاميم 3D

يمكن ضرب المصفوفة بمصفوفة عمودية إذا كانت أبعادهما تسمح بذلك، حيث يُعَد ذلك عمليةً أساسيةً في الرسوميات الحاسوبية وفي العديد من المجالات الأخرى؛ إذ تُجرَى هذه العملية ملايين المرات في الثانية عند تشغيل برنامج الرسوميات ثلاثية الأبعاد. سنوضح في هذا المقال المواضيع التالية: أبعاد معامَلات ونتيجة ضرب المصفوفات بمصفوفة عمودية. أبعاد معامَلات ونتيجة ضرب مصفوفة سطرية بالمصفوفات. ضرب المصفوفات بمصفوفة عمودية. ضرب مصفوفة سطرية بالمصفوفات. استخدام الجداء النقطي لضرب المصفوفات. الوصول إلى نتيجة ضرب المصفوفات من خلال تطبيق عمليات متعددة من الجداء النقطي. قلب Flipping المصفوفة العمودية عند ضرب المصفوفات بمصفوفة عمودية. قلب أعمدة المصفوفة عند ضرب مصفوفة سطرية بها. التعريفات الرياضية لعمليات ضرب المصفوفات وخطوات تنفيذها. الخاصية غير التبديلية لضرب المصفوفات. رأينا مسبقًا عمليات شبيهة بالضرب، والتي هي: ضرب عدد حقيقي (مقدار سلمي) Scalar بعدد حقيقي، والذي يعطي عددًا حقيقيًا. ضرب مصفوفة عمودية بعدد حقيقي، والذي يعطي مصفوفة عمودية. الجداء النقطي Dot Product للمصفوفات العمودية، والذي يعطي عددًا حقيقيًا. ضرب المصفوفات بالمصفوفة العمودية ناتج ضرب مصفوفةٍ ما بمصفوفة عمودية هو مصفوفة عمودية كما في المثال التالي: سنشرح لاحقًا تفاصيل كيفية تطبيق هذه العملية، ولكن لاحظ الآن أبعاد معامَلات العملية ونتيجتها؛ إذ يمكن تشكيل عملية ضرب مصفوفة بمصفوفة عمودية إذا كان عدد أعمدة المصفوفة مساويًا لعدد أسطر المصفوفة العمودية كما يلي: Matrix(R x N) x Col. Matrix(N x 1) = Resulting Col. Matrix(R x 1)‎‎ يمكن توضيح ذلك في المثال التالي: Matrix(2‎ x 2) x Col. Matrix(2‎ x 1) = Resulting Col. Matrix(2‎ x 1)‎ نعرض الأبعاد بالشكل: "Row x Column" (بحيث يكون Row هو عدد الصفوف وColumn هو عدد الأعمدة)، إذ تكون المصفوفة التي أبعادها R x 1 مصفوفةً عمودية، لأنها تحتوي على عمود واحد. لاحظ أيضًا كيف تكون أبعاد نتيجة ضرب مصفوفة بمصفوفة عمودية في المثال التالي: Matrix(5 x 5) x Col. Matrix(5 x 1) = Resulting Col. Matrix(5 x 1)‎ لنحدّد الآن ما إذا كان من الممكن ضرب مصفوفةٍ بمصفوفة عمودية وما هي أبعاد نتيجة عملية الضرب في الأمثلة الموجودة في الجدول التالي: أبعاد المصفوفة أبعاد المصفوفة العمودية أبعاد النتيجة الأبعاد 3‎ x 3 الأبعاد 3‎ x 1 الأبعاد 3‎ x 1 الأبعاد 3‎ x 2 الأبعاد 2‎ x 1 الأبعاد 3‎ x 1 الأبعاد 2‎ x 3 الأبعاد 2‎ x 1 غير ممكنة الأبعاد 4‎ x 3 الأبعاد 3‎ x 1 الأبعاد 4‎ x 1 الأبعاد 3‎ x 5 الأبعاد 5‎ x 1 الأبعاد 3‎ x 1 لاحظ أنه من غير الممكن تشكيل عملية الضرب التي تبدو كما يلي: ‎Matrix(2 x 1) x Col. Matrix(2 x 2) = Resulting Col. Matrix‎‎(غير ممكنة) وضع المصفوفة العمودية على الجهة اليمنى فقط من عملية الضرب إذا ضربنا مصفوفةً مستطيلةً بمصفوفة عمودية، فستكون المصفوفة العمودية دائمًا على يمين المصفوفة المستطيلة؛ إذ لا يمكن ضربهما إّلا إذا كان "البعد الداخلي Inner Dimension" (البعد M مثلًا) لكل مصفوفة متساويًا: Matrix(N x M) x Col. Matrix(M x 1) = Resulting Col. Matrix(N x 1)‎ حيث يمكن تشكيل عملية الضرب التي تبدو كما يلي: ‎Matrix(1 x 2) x Col. Matrix(2 x 1) = عدد حقيقي‎‎(1 x 1) استخدام الجداء النقطي لضرب المصفوفات يبدو استخدام الجداء النقطي لضرب المصفوفات ممكنًا من خلال النظر إلى الأبعاد المصفوفات، ولكنه ليس دليلًا على إمكانية ذلك. إليك المثال التالي: قد يبدو غريبًا بعض الشيء عَدُّ العدد الحقيقي (المقدار السلمي Scalar) كائنًا أبعاده "1 × 1"، ولكن تبقي هذه الطريقة الأمور متناسقةً فيما بينها. لاحظ أن هذا المثال يشبه الجداء النقطي (وهو كذلك فعلًا)، وبالتالي ستتشكّل عملية الضرب كما يلي: إذًا لنوجد الآن ناتج عملية الضرب التالية كما يلي: قلب المصفوفة العمودية من المفيد التفكير في "قلب" المصفوفة العمودية عند تشكيل الجداء النقطي ليحاذي كل صف من المصفوفة، ثم ضرب وجمع العناصر المتقابلة كما في المثال التالي: وفي المثال التالي أيضًا: لنشكّل الآن عملية الضرب التالية: تدريب عملي اُحسب الجداء النقطي في الجدول التالي. ستجد ناتج الجداء في عمود النتيجة: المعامل الأول المعامل الثاني النتيجة المصفوفة المصفوفة العمودية ‎‎ الناتج ‎-2 المصفوفة المصفوفة العمودية ‎‎ الناتج ‎-2 المصفوفة المصفوفة العمودية ‎‎ الناتج ‎2 سنستخدم عمليات الجداء النقطي السابقة لإيجاد نتيجة ضرب المصفوفة بالمصفوفة العمودية كما يلي: إذًا يمكننا الحصول على ناتج عملية ضرب مصفوفةٍ بمصفوفة عمودية من خلال تطبيق الجداء النقطي للمصفوفة العمودية مع كل صف من المصفوفة الأخرى، ولكن يجب أن تسمح أبعاد كل معامَل بذلك؛ إذ يساعد ذلك على قلب المصفوفة العمودية، بحيث يمكن محاذاة عناصرها مع عناصر المصفوفة كما يلي: اقلب المصفوفة العمودية واحسب النتيجة ما يلي: إليك أيضًا بعض عمليات الضرب الأخرى التي قد ترغب في التدرب عليها، ولكن تذكّر أن تقلب المصفوفة العمودية وتضعها فوق المصفوفة، ثم طبّق الجداء النقطي للمصفوفة العمودية التي قلبناها مع صف واحد من المصفوفة في كل مرة: العملية النتيجة الناتج ‎‎ الناتج الناتج ‎ استخدام عمليات متعددة من الجداء نقطي لإجراء عملية ضرب المصفوفة السطرية بالمصفوفات جرّب الآن إجراء العملية التالية: لاحظ أن أبعاد المصفوفات متوافقة، لذا يمكن إجراء العملية كما يلي: يمكنك أن ترى من المثال السابقة أنه يمكن إجراء عملية ضرب مصفوفةٍ سطرية بمصفوفةٍ ما من خلال تطبيق عدة عمليات جداء نقطية، ولكن يجب قلب أعمدة المصفوفة في هذه الحالة كما يلي: وضع المصفوفة السطرية على الجهة اليسرى من عملية الضرب لا يمكن إجراء النوع التالي من عمليات الضرب، لأن الأبعاد غير صحيحة: Matrix (3 x 4) x Row Matrix (1 x 3)‎ إذًا يجب أن تكون المصفوفة السطرية على الجهة اليسرى عند ضرب مصفوفة سطرية بمصفوفة مستطيلة، حيث تكون أبعاد المعامَلات والنتيجة كما يلي: Row Matrix (1 x M) x Matrix (M x C) = Result Row Matrix (M x C)‎ ملاحظة: المصفوفة التي أبعادها 1xC هي مصفوفة سطرية مكوَّنة من عددٍ "C" من الأعمدة. نوضّح في الأمثلة الموجودة في الجدول التالي ما إذا كانت عملية الضرب ممكنة وما هي أبعاد نتيجة العملية: المعامل الأول المعامل الثاني النتيجة 3‎ x 3 ‫ 3‎ x 1 ‫ 3‎ x 1 1‎ x 2 ‫ 2‎ x 2 ‫ 1‎ x 2 1‎ x 2 ‫ 2‎ x 3 ‫ 1‎ x 3 4‎ x 4 ‫ 3‎ x 1 ‫ غير ممكنة 1‎ x 5 ‫ 5‎ x 3 ‫ 1‎ x 3 لنحاول الآن إجراء عملية الضرب التالية: وينتج ما يلي: التعريفات الدقيقة لعمليات الضرب قد تشعر بعدم الارتياح عند تعريف العمليات الرياضية بهذه الطريقة غير الرسمية، لذا إليك بعض التعريفات الأدق: ضرب مصفوفة بمصفوفة عمودية Matrix times Column Matrix: ليكن لدينا المصفوفة A التي أبعادها M x C، والمصفوفة العمودية x التي أبعادها C x 1، ويكون ناتج الجداء Ax مصفوفة عمودية أبعادها M x 1؛ إذ يتشكّل عنصرها i من ناتج الجداء النقطي للصف i من المصفوفة A مع المصفوفة العمودية x. ضرب مصفوفة سطرية بمصفوفة: ليكن لدينا المصفوفة السطرية x التي أبعادها 1‎ x R والمصفوفة **A التي أبعادها R x M، ويكون ناتج الجداء *xA* مصفوفة سطرية أبعادها 1‎ x M، حيث يتشكّل عنصرها الأول من ناتج الجداء النقطي للمصفوفة السطرية x مع العمود i من المصفوفة A. لنحاول الآن إجراء عملية الضرب التالية: وسينتج لدينا ما يلي: خطوات إجراء عملية ضرب المصفوفات يتضمن الضرب دائمًا عمليات جداء نقطية للصفوف الموجودة على اليسار والأعمدة الموجودة على اليمين وفقًا للتعريفات السابقة، لذا يجب اتباع الخطوات التالية لإجراء أيٍّ من هذه الحسابات: دراسة أبعاد معاملات عملية الضرب حيث: يجب أن تكون الأبعاد الداخلية متساوية: 1xN و NxC. نتجاهل الأبعاد الداخلية للعثور على أبعاد النتيجة: 1xC. نكتب مصفوفة فارغة بالأبعاد الصحيحة لتمثّل المصفوفة الناتجة. ملء جميع عناصر المصفوفة الناتجة كما يلي: نقلب كل عمود موجود على اليمين إلى صف على اليسار. ينتج كل عنصر من عناصر المصفوفة الناتجة عن عملية جداء نقطي. تدريب عملي لا تُعَد Ax و xA متساويتين؛ فإذا كان تطبيق عملية الضرب Ax ممكنة، فستكون أبعاد xA غير متوافقة عند ذلك، ويمكن في بعض الأحيان تشكيل كلٍّ من هاتين العمليتين، ولكن النتائج ستكون مختلفة، وبالتالي يمكن القول أن ضرب المصفوفات ليست عمليةً تبديلية. إذًا لنختبر مهاراتك في الأمثلة التالية: العملية النتيجة الناتج الناتج الناتج وصلنا إلى نهاية هذا المقال الذي تعرّفنا من خلاله على ضرب مصفوفة بمصفوفة عمودية وضرب مصفوفة سطرية بمصفوفةٍ ما، وسنتعرّف في المقال التالي على كيفية ضرب مصفوفة مستطيلة بمصفوفة أخرى. ترجمة -وبتصرُّف- للفصل Matrix-Column Matrix Multiplicaton من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: تعرف على المصفوفات Matrices وعملياتها البسيطة في التصاميم 3D الجداء الشعاعي في التصاميم ثلاثية الأبعاد وخاصياته وحسابه كيفية جمع وطرح المصفوفات العمودية والمصفوفات السطرية الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد

تُستخدَم المصفوفات في العديد من المجالات لتمثيل كلٍّ من الكائنات والعمليات التي تُطبَّق عليها؛ إذ تُمثَّل النقاط والأشعة بالمصفوفات العمودية في الرسوميات الحاسوبية، وتُمثَّل العمليات عليها بمصفوفات مربّعة. سنناقش في هذا المقال المواضيع التالية: تعريف المصفوفة. عناصر المصفوفة. أبعاد المصفوفة. أسماء المصفوفات. تَساوي مصفوفتين. المصفوفة المربعة. عملية جمع المصفوفات وقواعدها. المصفوفة الصفرية. معاكس مصفوفة. طرح المصفوفات. ضرب المصفوفات بعدد حقيقي Scalar. منقول Transpose المصفوفة. تعريف المصفوفة تتكوّن المصفوفة العمودية من عمود واحد من الأعداد، ولكن يمكن ترتيب هذه الأعداد في عدة صفوف وعدة أعمدة، وبالتالي يمكن وضع الأعداد في مصفوفة ثنائية الأبعاد. إذًا المصفوفة هي مجموعة من الأعداد المرتَّبة ضمن عددٍ ثابت من الصفوف والأعمدة، وتكون هذه الأعداد أعدادًا حقيقية. يمكن أن تحتوي المصفوفات على أعداد معقدة أيضًا، ولكننا لن نراها في هذا المقال. إليك مثالًا لمصفوفة مكونة من ثلاثة صفوف وثلاثة أعمدة: الصف العلوي هو الصف 1، والعمود الموجود في أقصى اليسار هو العمود 1، والمصفوفة السابقة هي مصفوفة بحجم 3x3، لأنها تحتوي على ثلاثة صفوف وثلاثة أعمدة، ويكون التنسيق لوصف المصفوفات هو: rows X columns. يسمّى كل عدد يشكّل المصفوفة عنصرًا Element من عناصرها، ويكون للعناصر مواقع مُحدَّدة في المصفوفة؛ إذ تمثّل الزاويةُ العلوية اليسرى من المصفوفة الصفَّ 1 والعمود 1، وقيمة العنصر الموجود في الصف 1 والعمود 1 في المصفوفة السابقة هي 1، وقيمة العنصر الموجود في الصف 2 والعمود 3 هي 4.6، وقيمة العنصر في الصف 3 والعمود 1 هي 4. أبعاد المصفوفة يُطلَق مصطلح أبعاد المصفوفة على عدد صفوفها وأعمدتها. إليك فيما يلي مصفوفةً مكونةً من ثلاثة صفوف وعمودين: تُكتَب أحيانًا الأبعاد إلى جانب المصفوفة كما هو الحال في المصفوفة السابقة، ولكنه مجرد تذكير صغير وليس جزءًا من المصفوفة. إليك مثالًا آخر لمصفوفة ذات أبعاد مختلفة تتكون من صفين وثلاثة أعمدة، والتي تُعَد "نوع بيانات" مختلف عن المصفوفة السابقة: المصفوفة المربعة Square Matrix تحتوي المصفوفة المربعة Square Matrix على العدد نفسه من الصفوف والأعمدة، وتُستخدَم المصفوفات المربعة لتمثيل التحويلات الهندسية Transformations في الرسوميات الحاسوبية. المصفوفة المستطيلة Rectangular Matrix هي المصفوفة التي يمكن ألّا يكون لها العدد نفسه من الصفوف والأعمدة. مع ذلك، تطالب بعض المراجع بوجوب أن يكون عدد الصفوف مختلفًا عن عدد الأعمدة. أما المصفوفة العمودية Column Matrix فتتكون من عمود واحد، وهي مصفوفة بحجم N x 1، وقد استخدمنا المصفوفة العمودية في هذه السلسلة من المقالات لتمثيل الأشعة الهندسية مثل معظم كتب الرسوميات الحاسوبية. إليك مثالًا عن مصفوفة عمودية بحجم ‎:4 x 1 تتكون المصفوفة السطرية Row Matrix من صفٍ واحد، حيث تستخدم بعض الكتب المصفوفات السطرية لتمثيل الأشعة الهندسية. تسمّي بعض الكتب المصفوفة العمودية بالشعاع العمودي وتسمّي المصفوفة السطرية بالشعاع السطري، ويُعَد ذلك أمرًا جيدًا، ولكنه غامضٌ بعض الشيء، لذا سنستخدم في هذا المقال مصطلح شعاع Vector للتعبير عن كائن هندسي، وسنستخدم المصفوفات العمودية لتمثيل الأشعة، كما سنستخدمها أيضًا لتمثيل النقاط الهندسية. أسماء المصفوفات إذا نسيت ما إذا كانت الصفوف أو الأعمدة تأتي أولًا، فتذكر فقط مصطلح الأعمدة الرومانية ROWman COLumns. يمكن إعطاء اسمٍ للمصفوفة، ويكون هذا الاسم عادةً حرفًا إنجليزيًا كبيرًا بخط عريض في النصوص المطبوعة مثل A أو M، وتُكتَب في بعض الأحيان الأبعاد على يمين الحرف كما في المصفوفة ‎B3x3‎. لعناصر المصفوفة أسماءٌ أيضًا؛ إذ يكون اسم العنصر عادةً بحرفٍ مماثل لاسم المصفوفة، ولكنه حرفٌ صغير مع كتابة موضع العنصر بصورة منخفضة، لذلك يمكن مثلًا كتابة المصفوفة A التي أبعادها 3x3 على النحو التالي: يمكن أيضًا كتابة المصفوفة ‎A = [aij]‎ للقول بأن عناصر المصفوفة A تسمَّى aij‎. تساوي مصفوفتين إذا احتوت مصفوفتان على القيم نفسها، ولكن في مواقع مختلفة، فلا يمكن عَدّ هاتين المصفوفتين متساويتين، فلكي تكون المصفوفتان متساويتان، يجب أن يكون: لهما الأبعاد نفسها. يجب أن تكون العناصر المتقابلة متساوية. لنفترض أن لدينا المصفوفتين ‎A n x m = [aij]‎ و ‎B p x q = [bij]‎، وعندها يكون ‎A = B‎ إذا وفقط إذا كان n=p و m=q وaij=bij ‎ لجميع قيم i و j ضمن المجال المحدَّد. إليك مصفوفتين غير متساويتين بالرغم من أنهما تحتويان على العناصر نفسها: كما أن المصفوفتين التاليتين غير متساويتين، لأن عناصرهما المتقابلة غير متساوية بالرغم من لهما الأبعاد نفسها: جمع المصفوفات إذا كانت لدينا مصفوفتان لهما العدد نفسه من الصفوف والأعمدة، فيمكن حساب مجموعهما؛ حيث إذا كانت A مصفوفةً أبعادها MxN، وكانت B مصفوفةً أبعادها MxN، فإن مجموعهما هو مصفوفة أبعادها MxN مكوّنة من جمع العناصر المتقابلة للمصفوفتين A و B. إليك مثال عن جمع مصفوفتين: تكون عناصر المصفوفات أعدادًا حقيقية ذات كسور عشرية في معظم الحالات العملية، وليست أعدادًا صحيحة صغيرة كتلك المستخدمة غالبًا في أمثلتنا. المصفوفة الصفرية Zero Matrix يمكن جمع مصفوفة أبعادها 3x2 مع مصفوفة أخرى أبعادها 3x2 دون تغيير المصفوفة الثانية إذا كانت جميع عناصر المصفوفة الأولى أصفارًا، والتي تُسمَّى بالمصفوفة الصفرية. إليك مثال عن مصفوفة صفرية أبعادها 3x3: اسم المصفوفة الصفرية هو صفر مكتوب بخط عريض 0، بالرغم من أننا قد ننسى في بعض الأحيان كتابته بخط عريض. أوجد ناتج عملية الجمع التالية: المجموع بالطبع هو المصفوفة غير الصفرية نفسها. قواعد جمع المصفوفات سنوضّح فيما يلي قواعد جمع المصفوفات، إذ يفترض أن تكون للمصفوفات الأبعاد نفسها: A + B = B + A A + 0 = 0 + A = A 0 + 0 = 0 تشبه هذه القواعد بعض القواعد الخاصة بجمع الأعداد الحقيقية، ولكن انتبه إلى أنه ليست جميع قواعد رياضيات المصفوفات مماثلة لتلك الخاصة برياضيات الأعداد الحقيقية. تنص القاعدة الأولى على أن جمع المصفوفات هو عملية تبديلية Commutative، بسبب إجراء عملية الجمع العادي على العناصر المتقابلة في المصفوفتين، ويُعَد الجمع العادي (الحقيقي) تبديليًا. كما يُعَد جمع المصفوفات عملية تجميعية Associative، وهي قاعدة أخرى تماثل قواعد رياضيات الأعداد الحقيقية، بسبب إجراء عملية الجمع العادية على العناصر المتقابلة من المصفوفتين: ‎(A + B) + C = A + (B + C) لنوجِد ناتج جمع المصفوفتين التاليتين: لاحظ أن كل عنصر من عناصر المصفوفة الناتجة التي أبعادها 3x3 هو 10. ضرب المصفوفة بعدد حقيقي Scalar يمكن ضرب المصفوفة بعدد حقيقي (مقدار سلمي) من خلال ضرب كل عنصر من عناصر المصفوفة بهذا العدد. إليك مثال على ذلك، بحيث يكون المتغير a عددًا حقيقيًا: يكون كل عنصر في النتيجة معاكسًا للعنصر الأصل إذا كانت قيمة العدد الحقيقي a في المثال السابق تساوي ‎-1، كما سنرى في الفقرة التالية. معاكس المصفوفة يمكن تشكيل معاكس للمصفوفة من خلال تغيير إشارة كل عنصر من عناصر هذه المصفوفة: ‎-A = -1 A كما في المثال التالي: تنتج المصفوفة الصفرية عن جمع المصفوفة مع معاكسها. لاحظ أن الصفر الأخير هو صفر بخط عريض، والذي يعبّر عن المصفوفة الصفرية: A + (-A) = 0‎ ملاحظة: يمكن تعريف عملية الطرح مصفوفتين على أنها عملية جمع المصفوفة الأولى مع معاكس المصفوفة الثانية. طرح المصفوفات إذا كانت المصفوفتان A و B لهما العدد نفسه من الصفوف والأعمدة، فيمكن تعريف عملية الطرح ‎A - B‎ بأنها ‎A + (-B)‎؛ إذ يمكن حساب ‎A - B‎ من خلال طرح العنصر المقابل من المصفوفة B من كل عنصر من عناصر المصفوفة A. إليك مثال غير مكتمل عن طرح المصفوفات: لاحظ العناصر الموجودة في الصف الأول من الإجابة السابقة؛ إذ تُعَد طريقة حساب النتيجة للعناصر الموجودة في الصف 1 والعمود 2 مربكةً بعض الشيء. لنحاول الآن وضع الإجابة مكان علامتي الاستفهام في المثال السابق كما يلي: منقول مصفوفة Transpose منقول المصفوفة هو مصفوفة جديدة تكون صفوفها هي أعمدة المصفوفة الأصلية، مما يؤدي أيضًا إلى جعل أعمدة المصفوفة الجديدة هي صفوف المصفوفة الأصلية. إليك مثال عن مصفوفة ومنقولها: الحرف المرتفع "T" يعني المنقول "Transpose". هناك طريقة أخرى للنظر إلى المنقول، وهي أن العنصر الموجود في الصف r والعمود c في المصفوفة الأصلية يُوضَع في الصف c والعمود r من المنقول؛ إذ يصبح العنصرُ ‎arc‎ في المصفوفة الأصلية هو العنصر ‎acr‎ في المصفوفة المنقولة. نتعامل عادةً مع المصفوفات المربعة لإيجاد منقولها، ولكن يمكن نقل المصفوفات غير المربعة أيضًا مثل المصفوفة التالية: إليك مثال آخر عن كيفية إيجاد منقول مصفوفة غير مربعة: قاعدة خاصة بمنقول المصفوفة إذا أوجدنا المنقول لمنقول المصفوفة نفسها، فستحصل على المصفوفة الأصلية مرةً أخرى كما في المثال التالي: ويوضح المثال السابق القاعدة: ‎(AT)T = A‎‎. لاحظ أن منقول مصفوفة سطرية هو مصفوفة عمودية، وبالتالي فإن منقول مصفوفة عمودية هو مصفوفة سطرية كما في المثال التالي: المصفوفة المتناظرة Symmetric Matrix المصفوفة المتناظرة هي المصفوفة التي تتساوى مع منقولها، أي: ‎AT = A‎، ولكن يجب أن تكون مصفوفةً مربعة. إليك فيما يلي مثال عن بعض المصفوفات المتناظرة: إذا كانت المصفوفة متناظرة، فستكون عناصرها ‎aij = aji‎. ملاحظة: تُعَد المصفوفة الصفرية مصفوفةً متناظرةً أيضًا. قطر المصفوفة الرئيسي Main Diagonal يتكوّن القطر الرئيسي للمصفوفة من العناصر التي تقع على القطر الذي يمتد من أعلى يسار المصفوفة إلى أسفل يمينها، فإذا كانت لدينا المصفوفة A مثلًا، فإن عناصر قطرها الرئيسي هي العناصر التي يتساوى فيها رقم الصف مع رقم العمود ‎ajj‎. لا يُعَد القطر الآخر للمصفوفة مهمًا وليس له اسم. ملاحظة: عناصر المصفوفة A التي لا تتغير عند تشكيل المنقول ‎AT‎، هي العناصر الموجودة على طول القطر الرئيسي، لأن العناصر ‎ajj‎ في المصفوفة A هي العناصر نفسها في المنقول ‎AT‎. الخلاصة إليك بعض القواعد التي ناقشناها في هذا المقال؛ إذ يجب عليك فهمها بدلًا من حفظها، حيث تحتوي المصفوفات في كل قاعدة من القواعد التالية على العدد نفسه من الصفوف والأعمدة: ‎A + 0 = A‎ ‎A + B = B + A‎ 0 + 0 = ‎0 ‎A + (B + C) = (A + B) + C‎‎ ‎(ab) ‎A = a(b A) ‎a(A + B) = a B + a A‎‎ ‎a 0 = 0‎ ‎(-1) ‎A = -A A - A = 0‎ ‎(AT)T = A 0T = 0‎ حيث أن a و b هي مقادير سلمية (أعداد حقيقية)، و A و B مصفوفتان، و 0 هي المصفوفة الصفرية ذات البعد المناسب. ملاحظة: إذا كان ‎A = B‎ و ‎B = C‎، فإن ‎A = C‎. وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على المصفوفات وعملياتها البسيطة، وسنناقش في المقال التالي مزيدًا من الأمور التي يمكن تطبيقها باستخدام المصفوفات. ترجمة -وبتصرُّف- للفصل Matrices and Simple Matrix Operations من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: الجداء الشعاعي في التصاميم ثلاثية الأبعاد وخاصياته وحسابه كيفية جمع وطرح المصفوفات العمودية والمصفوفات السطرية الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد.

يُعَد الجداء الشعاعي عمليةً تستخدم شعاعين على أساس معامَلين. وتكمن أهمية هذا في الرسوميات الحاسوبية عند محاولة العثور على شعاع عمودي على مستوٍ؛ ويُعَد ذلك ضروريًا عند حساب كيفية انعكاس الضوء على السطوح. سنوضّح في هذا المقال المواضيع التالية: تعريف الجداء الشعاعي لشعاعين. قاعدة اليد اليمنى: يكون منحى Orientation الجداء الشعاعي ‎u × v‎ باتجاه "الإبهام" إذا طويت أصابعك من الشعاع u إلى الشعاع v. خاصيات الجداء الشعاعي والتي هي: حجم Magnitude الجداء الشعاعي: حجم الجداء الشعاعي u × v هو مساحة متوازي الأضلاع التي يحدّدها هذان الشعاعان. لا يُعَد الجداء الشعاعي عملية تبديلية Anti-commutative: u × v = -(v × u)‎‎ u × u = 0‎ و (ku) × u = 0 نتيجة الجداء الشعاعي لشعاع مع شعاع صفري هي شعاع صفري: u × 0 = 0 × u = 0‎ لا يُعَد الجداء الشعاعي عملية تجميعية: ‎(u × v) × w ≠ u × (v × w) إمكانية توزيع الجداء الشعاعي على جمع الأشعة: u × (v + w) = u × v + u × w‎ الجداء الشعاعي بين محاور الإحداثيات: i × j = k و j × k = i و k × i = j حساب الجداء الشعاعي باستخدام المصفوفات العمودية. استخدام أداة مساعدة شبيهة بمحدّدات المصفوفات Determinant لتذكّر صيغة حساب الجداء الشعاعي للمصفوفات العمودية. تذكير: يكون نوع الكائنات التي تمثّلها معامَلات الجداء النقطي أشعةً، وتكون نتيجة الجداء النقطي عددًا حقيقيًا (مقدارًا سلميًا) Scalar. لقد شاهدت حتى الآن العمليات التالية: ولكن لا توجد عملية تشبه الضرب وتأخذ شعاعين كمعامَلين وينتج عنها شعاع، وهذا ما يمثله جداء الأشعة الشعاعي الذي سنشرحه في هذا المقال. تعريف الجداء الشعاعي إذا كان u و v شعاعين في فضاء ثلاثي الأبعاد، فإن الجداء الشعاعي لهما ‎u × v‎ هو شعاع ثلاثي الأبعاد، ويجب أن تكون معاملات هذه العملية ونتيجتها أشعةً ثلاثية الأبعاد على عكس العمليات الأخرى؛ إذ أن عملية الجداء الشعاعي ليست مُعرَّفةً في الفضاء ثنائي الأبعاد 2D. يمكن تعريف الجداء الشعاعي لشعاعين u × v كما يلي: يجب أن يكون u و v شعاعين ثلاثي الأبعاد. والنتيجة هي شعاع ثلاثي الأبعاد مع الطول والمنحى التاليين: الطول: ‎|‎ u × v | = | u | | v | sin θ حيث θ هي الزاوية بين الشعاعين u و v. المنحى: يكون ناتج الجداء الشعاعي u × v عموديًا على كلٍّ من الشعاعي u و v. يجري الاختيار من بين منحيين متعامدين على الشعاعين u و v باستخدام قاعدة اليد اليمنى. ناتج الجداء الشعاعي لشعاعين هو شعاع عمودي على هذه الشعاعين، ولكن هناك اتجاهين متعامدين على كلٍّ من هذين المعامَلين، حيث يمكن الاختيار من بينهما باستخدام قاعدة اليد اليمنى، والتي سنشرحها في الفقرة التالية. قاعدة اليد اليمنى Right-hand Rule نضع البرغي الخشبي عموديًا على لوحٍ من الخشب، ونلفّه باتجاه اللوح الخشبي باستخدام مفك براغي؛ إذ يجب أن ندير البرغي اليميني (النوع العادي) باتجاه عقارب الساعة من رأسه إلى اللوح الخشب. يكون الجداء الشعاعي لشعاعين متعامدًا عليهما، وتختار قاعدة اليد اليمنى أحد الاتجاهين المتعامدين المُحتمَلين. ويوضح الرسمان البيانيان السابقان هذه القاعدة. لا تنسَ أن ترتيب المعاملات مهم، إذ تؤشّر نتيجة الجداء الشعاعي ‎u × v‎ إلى الاتجاه نفسه الذي يجب أن يؤشّر إليه البرغي، إذا دفع الالتفافُ من الشعاع u إلى الشعاع v البرغي إلى داخل قطعة الخشب، أو فكّر في الاتجاه الذي يؤشّر إليه إبهامك عندما تطوي أصابعك من الشعاع u إلى الشعاع v. ملاحظة: يؤشّر الجداء الشعاعي ‎u × v‎ و ‎v × u‎ إلى اتجاهين متعاكسين. تصور الجداء الشعاعي يُظهر الشكل التالي الشعاعين u و v ومتوازي الأضلاع المُحدَّد بينهما. مساحة متوازي الأضلاع هي: ‎| ‎u | | v | sin θ، حيث θ هي الزاوية بينهما. تمثّل هذه المساحة حجم الجداء الشعاعي، وتكون هذه الحقيقة مفيدةً أحيانًا لتصور الجداء الشعاعي، فإذا دوّرنا الشعاع u مثلًا، بحيث يقترب منحاه من منحى الشعاع v (دون تغيير طوله)، فستقترب مساحة متوازي الأضلاع وحجم الجداء الشعاعي من الصفر، بينما تعطي الزاوية 90 درجة بين الشعاعين u و v القيمة العظمى للجداء الشعاعي. عكس ترتيب معاملات الجداء الشعاعي تذكير: يمكن عكس اتجاه الشعاع w من خلال ضربه بالعدد ‎-1؛ إذ يؤشّر الشعاعان w و ‎-w إلى اتجاهين متعاكسين. يوضح الشكل السابق حاصل عمليتي جداء شعاعين حدّدنا منحاهما باستخدام قاعدة اليد اليمنى، ويكون حجم الجداء الشعاعي: ‎‎u × v‎ = ‎| u | | v | sin θ = | v | | u | sin θ‎‎ وبالتالي: ‎u × v‎ = -(v × u)‎‎ ويمكن القول أن: ‎-(v × u) = -v × u‎‎‎ المعاملات المتوازية للجداء الشعاعي طول ‎u × v‎ هو ‎| u | | v | sin θ، وإذا كان u و v شعاعين على استقامة واحدة Collinear (متوازيين)، فإن الزاوية بينهما θ = 0، وبالتالي سيكون sin θ = 0، وحجم ناتج الجداء الشعاعي يساوي الصفر، ولكن النتيجة هي شعاع؛ وبالتالي تكون نتيجة الجداء الشعاعي هي الشعاع الصفري 0. u × u = 0 بما أن k u‎ على استقامة واحدة مع الشعاع u (حيث k عدد حقيقي)، فسيكون: ‎(k u) × u = 0 نتيجة الجداء الشعاعي u × u = 0 عمودية على كلا المعامَلين، لأن ‎0‎ · u = 0، مما يعني أنهما متعامدان؛ فالشعاع الصفري 0 عمودي على جميع الأشعة كما مر معنا سابقًا. حجم الجداء الشعاعي ‎u × 0‎ وهو ‎| u | | 0 | sin θ يساوي الصفر، والنتيجة هي شعاع، وبالتالي: u × 0 = 0 × u = 0‎ لنوجد الآن الجداء الشعاعي ‎(k u) × v‎ من خلال الاطلاع على الرسم البياني السابق، أو من خلال العمل بالصيغة التالية: ‎(k u) × v = k( u × v‎ ) وسينتج ما يلي: | (k u) × v | = | k u | | v | sin θ = | k | | u | | v | sin θ إذًا يكون حجم ‎(k u) × v أكبر بمقدار | k | عن حجم u × v مع إبقاء الاتجاه نفسه. ليس الجداء الشعاعي للأشعة عملية تجميعية لا يُعَد الجداء الشعاعي للأشعة عمليةً تجميعية، ويمكن رؤية ذلك من خلال النظر إلى الرسم البياني السابق، ثم تشكيل الجداء الشعاعي (‎u × v‎)، ثم إجراء الجداء الشعاعي للناتج مع الشعاع w. نشكّل بعد ذلك حاصل الجداء الشعاعي (‎v × w‎)، ثم نجري الجداء الشعاعي للناتج مع الشعاع u؛ وينتج لدينا ما يلي: ‎(u × v) × w ≠ u × (v × w) لاحظ أن ناتج الجداء الشعاعي للشعاعين u × v من الرسم البياني السابق يساوي الشعاع الصفري 0، لأنهما على استقامة واحدة. إمكانية توزيع الجداء الشعاعي على جمع الأشعة توجد خاصية أخرى للجداء الشعاعي، وهي إمكانية توزيع الجداء الشعاعي على عملية جمع الأشعة كما يلي: u × (v + w) = u × v + u × w‎ ويمكن الوصول إلى هذه الخاصية من خلال التعويض في الصيغة التي تعرّف الجداء الشعاعي. الجداء الشعاعي بين محاور الإحداثيات تسمَّى أشعة الوحدة Unit Vectors التي تكون باتجاه المحاور x و y و z (في أيّ إطار إحداثي مُستخدَم)، i و j و k في أغلب الأحيان، وتوضَع أحيانًا قبعات صغيرة على كل حرف كما في الشكل التالي: بما أن طول كل شعاع من هذه الأشعة يساوي 1، وهي أشعة متعامدة فيما بينها، فإن جيب Sine الزاوية بين أيّ شعاعين منها يساوي 1.0، وستكون الصيغ التالية صحيحة: i × j = k‎ j × k = i‎ k × i = j‎ i × k = - ‎j k × j = - ‎i j × i = - k‎‎ i × i = 0‎ j × j = 0‎ k × k = 0‎ ولكن يُفضَّل رسم الرسم البياني ثم استخدام قاعدة اليد اليمنى بدلًا من حفظها. الجداء الشعاعي للمصفوفات العمودية نعرّف الجداء الشعاعي لمصفوفتين عموديتين ‎u × v‎ كما يلي: يجب أن تمثّل المصفوفتان العموديتان u و v أشعة ثلاثية الأبعاد. تمثّل النتيجة شعاعًا ثلاثي الأبعاد. إذا مثّلنا الشعاع u بالمصفوفة العمودية: ‎u = (ui, uj, uk)T‎ ومثّلنا الشعاع v بالمصفوفة العمودية: ‎v = (vi, vj, vk)T‎ فإن: ‎‎u × v = ( uj vk - uk vj, uk vi - ui vk , ui vj - uj vi )T‎‎ ملاحظة: لا تفكر في حفظ النتيجة السابقة، بل حاول إيجاد نمط محدّد لتشكيلها. لنوجد الآن الجداء الشعاعي ‎(1, 2, 3)T × (0, 0, 0)T‎: لاحظ أن: ‎(1, 2, 3)‎T × 0 = 0 أو يمكنك التعويض في صيغة الجداء الشعاعي للمصفوفات العمودية: ‎(1, 2, 3)T × (0, 0, 0)T = ( 2×0 - 3×0, 3×0 - 1×0, 1×0 - 2×0)T = 0 طريقة مساعدة لتذكر صيغة الجداء الشعاعي للمصفوفات العمودية سنوضّح الآن طريقة لحساب الجداء الشعاعي من خلال ترتيب عناصر كل شعاع في محدّد مصفوفة Determinant، والذي يساعدك لتذكر صيغة الجداء الشعاعي السابقة الصعبة جدًا، ولكن إذا كنت تعرف مسبقًا كيفية تقييم المحدّدات ذات الحجم 3x3، فيمكنك تخطي هذه الطريقة، واستخدام الصيغة الموجودة في التعريف. يحتوي الصف العلوي من المحدّد على الرموز التي تمثل كل محور، ولكن تذكّر أن هذه الطريقة لا تمثّل تعريف الجداء الشعاعي، ولا تمثّل محدد مصفوفة، ولكنها مجرد أداة مساعدة للتذكر. تعمل هذه الطريقة فقط مع الأشعة ثلاثية الأبعاد، إذ لم يُعرَّف الجداء الشعاعي إلّا للأشعة في الفضاء ثلاثي الأبعاد، لذا ضع مكونات الشعاع الأول في الصف الثاني من المحدّد، ومكونات الشعاع الثاني في الصف الثالث. تدريب عملي تدريب1: لنوجِد الجداء الشعاعي للمصفوفتين العموديتين ‎(1, 2, 1)T‎ و ‎(0, -1, 2)T‎ كما يلي: ولنقيّم الآن النتيجة من خلال البحث عن العوامل المساعدة للمكوّن i و j و k التي أحطناها بدائرة حمراء في الصف العلوي؛ فالعوامل المساعدة للمكوّن i مثلًا هي عناصر الصفين 2 و 3 التي ليست موجودة في العمود i. يمكن إيجاد العامل المساعد من خلال ضرب العنصرين الموجودين على القطر الرئيسي، ثم طرح حاصل ضرب العنصرين الموجودين على القطر الآخر من نتيجة ضرب العنصرين الموجودين على القطر الرئيسي، فعلى سبيل المثال، يكون العامل المساعد للمكوّن i هو 2×2 - 1×(-1) = 2 + 1 = 5. تدريب2: يكون حاصل الجداء الشعاعي للمصفوفتين العموديتين ‎(0, -1, 2)T‎ و ‎(1, 2, 1)T‎ كما يلي (لاحظ أننا عكسنا ترتيب الشعاعين السابقين): يتبع تقييم هذا المثال نمط المثال السابق نفسه، ولكن مع تبديل الصفين الثاني والثالث كما يلي: لاحظ أن النتيجة تمثّل معاكس النتيجة السابقة، مما يدل على أن: u × v = -(v × u)‎ ولقد رأينا ذلك سابقًا عندما استخدمنا الأشعة الهندسية. الجداء الشعاعي لمصفوفة عمودية مع نفسها يبقى الصفان الثاني والثالث كما هما عندما نأخذ الجداء الشعاع لشعاعٍ مع نفسه، وتذكّر من دروس الرياضيات في المرحلة الثانوية أنه إذا كان صفان من المحدّد متماثلين، فستكون قيمته صفرًا؛ حيث يكون كل عامل مساعد صفرًا، مما يؤدي إلى أن: 0‎ i + 0 j + 0 k = 0‎‎ يحدث الشيء نفسه إذا كان أحد الصفوف مضاعفًا للآخر؛ إذ تعكس هذه النتائج ما رأيناه مسبقًا مع الأشعة الهندسية: k u × u = 0‎ تنطبق أيضًا الخاصيات الأخرى لحاصل الجداء الشعاعي للأشعة الهندسية على حاصل الجداء الشعاعي لتمثيلاتها باستخدام المصفوفات العمودية. وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية حساب الجداء الشعاعي للأشعة، وسنتعرّف في المقال التالي على المصفوفات المستطيلة وعملياتها. ترجمة -وبتصرُّف- للفصل Vector Cross Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: إسقاط شعاع على شعاع آخر واستخداماته في الرسوميات الحاسوبية 3D تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D الجداء النقطي وارتباطه بطول الأشعة وتعامدها في التصاميم 3D

رأينا في المقالات السابقة أن نستطيع استخدام الجداء النقطي Dot Product من أجل الآتي: حساب طول الشعاع: حيث يكون الجداء النقطي للشعاع مع نفسه = الطول2. اكتشاف التعامد بين شعاعين: حيث يكون الجداء النقطي لشعاعين متعامدين = 0. حساب الزاوية بين شعاعين: حيث يكون cosθ = حاصل الجداء النقطي لشعاعي وحدة Unit Vectors. لن نضيف في هذا المقال شيئًا جديدًا عمّا تعلمناه في المقال السابق، ولكننا سنوسّع مفهوم حساب الزاوية بين شعاعين ليشمل حساب الزاوية بين شعاعين في فضاء ثلاثي الأبعاد. سنتعرّف في هذا المقال على المواضيع الآتية: صيغة حساب جيب تمام Cosine الزاوية بين أشعة الوحدة. قائمة بالخطوات التي يجب اتخاذها لتطبيق هذه الصيغة على الأشعة التي ليست أشعة وحدة. استخدام الأشعة في مسائل الهندسة الفراغية. الزوايا في الفضاء ثلاثي الأبعاد تقع أي حافتين من الحواف الثلاثة المشكّلة لزاوية في صندوق من الورق المقوى في مستوٍ واحد، وتساوي الزاوية بينهما 90 درجة، إذ تتقاطع جميع حواف الصندوق بزوايا قائمة، ولكن لن تساوي الزوايا بين الحواف 90 درجة عادةً عند إسقاط الحواف لتكوين صورة ثنائية الأبعاد. الزوايا بين محاور الإحداثيات لا يؤدي تغيير مجال رؤيتك إلى تغيير الكائنات ثلاثية الأبعاد، ولكن ستتغيّر الصورة ثنائية الأبعاد. تعتمد الزاوية بين شعاعين في الفضاء ثلاثي الأبعاد على علاقتهما ببعضهما البعض، ولا تعتمد على مجال رؤيتك أو إطار الإحداثيات الذي تستخدمه؛ ولكن زوايا الصورة تعتمد كثيرًا على مجال الرؤية عندما تعرض صورة ثنائية الأبعاد مشهدًا ثلاثي الأبعاد. رأينا في المقال السابق الصيغة التالية لحساب الزاوية θ بين شعاعي الوحدة: au · bu = cosθ‎ إذًا لنطبّق هذه الصيغة على شعاعي الوحدة الموازيين للمحور x والمحور y وهما: ‎(1,0,0)T‎ و ‎(0,1,0)T‎ لحساب الزاوية المحصورة بين المحورين x و y كما يلي: ‏‏‎(1,0,0)T ‎· (0,1,0)T =‎ 0 وبالتالي فإن المحورين x و y متعامدان كما توقعنا. الزاوية بين شعاعين كان المثال السابق سهل التصور والحساب، إذًا لنجرب شيئًا أصعب، حيث يظهر الشكل الآتي شعاعين: الشعاع a الذي تمثله المصفوفة العمودية ‎(4,4,4)T‎. الشعاع b الذي تمثله المصفوفة العمودية ‎(4,0,4)T‎. لاحظ أن الزاوية بين الشعاعين لا تساوي 90 درجة، وبالتالي يصعب رؤيتها مقارنةً بالمثال السابق. يمكن أن نخمّن بصريًا إلى حدٍ ما أن الزاوية بين الشعاعين a و b أقل من منتصف المسافة بين المستوي العمودي والأفقي، إذ تكون الزاوية التي تساوي 35 درجة تخمينًا جيدًا، ولكن التخمين غير كافٍ ونحتاج صيغةً لحساب الزاوية، وهذا ما سنوضّحه في الفقرة التالية. صيغة حساب الزاوية بين شعاعين لاحظ أنه عند الانتقال من ذيل الشعاع a إلى رأسه تزيد المسافة العمودية بمقدار 4، بينما تزيد المسافة الأفقية بمقدار 4‎ √2، وظل الزاوية Tangent هو: 4‎ / (4 √2) = 1.0/ √2 = 0.7071 وبالتالي فإن الزاوية مع المستوي الأفقي هي: arctan( 0.7071 )‎ =‫ 35.26 درجة. وبما أن الشعاع b يقع في المستوي الأفقي، فإن الزاوية بين الشعاعين يجب أن تساوي هذه القيمة. وبالتالي فإن صيغة حساب الزاوية θ بين شعاعي وحدة هي: au · bu = cosθ ويمكننا استخدام هذه الصيغة مع الأشعة التي ليست أشعة وحدة باتباع الخطوات التالية: توحيد Normalize كل شعاع. حساب الجداء النقطي لشعاعي الوحدة الناتجين. استخدم arc cos للحصول على الزاوية. لنطبّق هذه الصيغة على الشعاع a الذي تمثله ‎(4,4,4)T‎ والشعاع b الذي تمثله ‎(4,0,4)T‎ كما يلي: ‎| a | = √(16 + 16 + 16) = 4√3 و | b | = √(16 + 16) = 4√2 au = (4, 4, 4)T / (4√3)‎ و au = (4, 0, 4)T / (4 √2 ) au · bu = (16 + 16)/( (4√3)(4 √2) ) = 2/(√3√2 ) = √2 /√3 = cosθ‎ cosθ = 0.81649 وبالتالي فإن الزاوية بين الشعاعين هي: θ =‫ 35.26 درجة. لا تُعَد الحسابات الكثيرة في التمرين السابق هي الغرض الحقيقي، ولكن الهدف هو توضيح الصيغة ‎au · bu = cosθ، والتي تُعَد مهمةً في كل جزء من أجزاء الرسوميات ثلاثية الأبعاد. تدريب عملي يوضح الشكل الآتي شعاعين تمثّلهما المصفوفتان العموديتان التاليتان: f = (2, 4, 6)T‎ ‎g = (6, 4, 3)T يمكن أن ترغب في قياس الزاوية بين الشعاعين من خلال وضع مِنقلة مسطحة بين الشعاعين، ولكن لا يمكنك ذلك لأن كل ما تراه هو إسقاطٌ للشعاعين على الشاشة. يمكننا تخمين الزاوية التي تفصل بين الشعاعين بمقدار 30 درجة، ولكنه مجرد تخمين، إذًا لنطبّق الصيغة لمعرفة مدى صحة هذا التخمين. أولًا، نحسب الأطوال وهي: ‎| f |2 = (2, 4, 6)T · (2, 4, 6)T = 4 + 16 + 36 = 56 ‎| g |2 = (6, 4, 3)T · (6, 4, 3)T = 36 + 16 + 9 = 61 ثانيًا، نوحّد الشعاعين كما يلي: fu = (2, 4, 6)T / √56‎ gu = (6, 4, 3)T / √61‎ ثالثًا، نحسب الجداء النقطي لهما وهو: fu · gu = (2, 4, 6)T · (6, 4, 3)T / ( √56 √61) = (12+16+18)/( √56 √61) = 46 / ( √56 √61) = 0.78704‎ رابعًا، نحسب الزاوية بينهما كما يلي: cos θ = 0.78704‎ θ = arc cos 0.78704 = 38.1‎ درجة لاحظ أن الجواب ليس بعيدًا جدًا عن التخمين. الزاوية بين اتجاهي شعاعين ليس من الضروري أن يتلامس الشعاعان عند ذيليهما حتى تكون هناك زاوية بينهما، فليس للأشعة موضع محدد، إذ يمكنك أخذ الجداء النقطي لأي شعاعين ثلاثي الأبعاد أو المصفوفات العمودية التي تمثلها. قد يبدو من الغريب قياس الزاوية بين الأشياء التي ليس لها موضع محدد، ولكن العديد من الظواهر لها منحًى Orientation، دون أن يكون لها موضع محدد؛ إذ قد تأتي الرياح من الغرب في أحد الأيام، ومن الشمال في اليوم التالي (بفارق 90 درجة)؛ وقد يصل ضوء الشمس عند الظهيرة في الصيف بزاوية مختلفة عن زاوية وصوله عند الظهيرة في الشتاء. يستخدم التظليل في الرسوميات ثلاثية الأبعاد أشعةً لمنحى السطح، وأشعة أخرى لاتجاه كل مصدر للضوء. ليكن باسم وبلال جالسين على الشاطئ، ويريدان تسمير بشرتهما كما في الشكل التالي: يؤشر إطار الإحداثيات المناسب إلى المحور x شمالًا، والمحور y للأعلى بصورة مستقيمة والمحور z شرقًا، حيث يكون الاتجاه نحو الشمس في هذا الإطار هو ‎(-3, 4, 0)T / 5، وشعاع الوحدة العمودي على ظهر باسم هو ‎( -1, 2, 2)T / 3، وشعاع الوحدة العمودي على ظهر بلال هو ‎( -2, 1, 2)T / 3. إذًا سيكون أحدهما متمتعًا بأفضل موضع للتسمير السريع، حيث سنوضّح ذلك كما يلي: الاتجاه نحو الشمس = ‎( -3, 4, 0)/5. الاتجاه العمودي على ظهر باسم = ‎( -1, 2, 2)/3. الاتجاه العمودي على ظهر بلال = ‎( -2, 1, 2)/3. يجب أن يكون ظهرك مُوجَّهًا مباشرةً نحو الشمس ليصل إليك أكبر قدرٍ من أشعتها، كما يجب أن تكون الزاوية بين الاتجاه العمودي على ظهرك واتجاه الشمس صغرى. بالنسبة لباسم: ‎( -1, 2, 2)/3 · ( -3, 4, 0)/5 = (3+8+0)/15 = 11/15 arc cos( 11/15 ) = 42.8‎ درجة وبالنسبة لبلال: ‎( -2, 1, 2)/3 · ( -3, 4, 0)/5 = (6+4+0)/15 = 10/15 arc cos( 14/15 ) = 48.2 درجة وبالتالي سيحصل باسم على تسمير لبشرته بصورة أسرع. تدريبات عملية تدريب 1: يظهر الرسم البياني الآتي الشعاعين التاليين: q = (-2, 4, 3)T p = (3, 1, -4)T وضعنا ذيل الأشعة عند نقطة الأصل لسهولة التصور، إذ تؤشّر الأشعة إلى ثُمنَين Octants مختلفتين من الفضاء ثلاثي الأبعاد. لنحسب الآن الزاوية بين هذين الشعاعين كما يلي: أولًا، نحسب الأطوال وهي: ‎| p |2 = ( -2, 4, 3)T · ( -2, 4, 3)T = 4 + 16 + 9 = 29 ‎| q |2 = ( 3, 1, -4)T · ( 3, 1, -4)T = 9 + 1 + 16 = 26 ثانيًا، نوحّد الشعاعين كما يلي: pu = (-2, 4, 3)T / √29‎ qu = (3, 1, -4)T / √26‎ ثالثًا، نحسب الجداء النقطي لهما وهو: pu · qu = (-2, 4, 3)·(3, 1, -4)T / ( √29 √26) = (-6 + 4 - 12)/( √29 √26) = -14/( √29 √26) = -0.50985‎ رابعًا، نحسب الزاوية بينهما كما يلي: cos θ = -0.50985 θ = arc cos( -0.50985) = 120.654‎ درجة تدريب2: أوجد جيب تمام الزاوية بين شعاعي الوحدة التاليين: s = (1, 0, 1)T /√2‎ t = (1, 1, 1)T /√3‎ cosθ = (1, 0, 1)T · (1, 1, 1)T / ( √2 √3) = 2 / ( √2 √3) = √2 / √3 = 0.8164‎ استخدام صيغة الجداء النقطي لحل المسائل الهندسية يمكن استخدام صيغة الجداء النقطي لحل بعض المسائل الهندسية التي قد تكون صعبة الحل، فمثلًا، تتطابق الحواف الحمراء في الشكل التالي على محاور الإحداثيات، وتشترك في نقطة النهاية (0, 0, 0)، وتنتهي الحافة على طول المحور x عند x=2، وتنتهي الحافة على طول المحور y عند y=3، وتنتهي الحافة على طول المحور z عند z=4، وتربط الحواف المتبقية نقاط النهاية هذه. لنفترض الآن أنك تريد حساب الزاوية بين الحافتين الخضراويتين، وقد يكون ذلك مملًا إلى حدٍ ما باستخدام علم المثلثات، لذا يمكنك: تشكيل شعاع لكل حافة خضراء (من خلال طرح نقاط النهاية). توحيد كل شعاع منهما. استخدام قاعدة الجداء النقطي لحساب الزاوية بينهما. إذًا لنطبّق هذه الخطوات لحساب الزاوية بين الحافتين الخضراويتين كما يلي: أولًا، نقاط النهاية هي: (0‎, 3, 0) إلى (2‎, 0, 0) (0‎, 3, 0) إلى (0‎, 0, 4) ثانيًا، نحسب أشعة الإزاحة وهي: a = (2, 0, 0) - (0, 3, 0) = (2, -3, 0)T‎ b = (0, 0, 4) - (0, 3, 0) = (0, -3, 4)T‎ ثالثًا، نحسب الأطوال كما يلي: ‎| a |2 = (2, -3, 0)T · (2, -3, 0)T = 13 ‎| b |2 = (0, -3, 4)T · (0, -3, 4)T = 25 رابعًا، نوحّد الأشعة كما يلي: au = (2, -3, 0)T / √13‎ bu = (0, -3, 4)T / 5‎ خامسًا، نحسب الجداء النقطي لهما: au · bu = (2, -3, 0)T · (0, -3, 4)T / (5 √13) = 9 / (5 √13) = 0.49923‎ سادسًا، نحسب الزاوية بينهما كما يلي: cosθ = 0.49923‎ θ = arc cos 0.49923 = 60.051‎ درجة إذا حسبتَ أشعة الإزاحة بالطريقة المعاكسة (بالطرح من ‎(0, 3, 0)‎)، فلن يؤثر ذلك على الإجابة، إذ يمكن أن يؤشّر شعاعان إلى اتجاهين متعاكسين، ولكن حاصل جدائهما النقطي سيكون نفسه. بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على كيفية حساب الزاوية بين شعاعين في فضاء ثلاثي الأبعاد، وسنتعرّف في المقال التالي على إسقاط شعاعٍ ما على شعاع آخر. ترجمة -وبتصرُّف- للفصل The Angle between 3D Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: كيفية إيجاد الزاوية بين شعاعين في فضاء ثنائي الأبعاد 2D الجداء النقطي وارتباطه بطول الأشعة وتعامدها في التصاميم 3D تطبيق الجداء النقطي Dot Product على الأشعة في التصاميم 3D تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D

ناقشنا في المقال السابق بعض استخدامات الجداء النقطي والتي هي: حساب طول الشعاع: حيث يكون الجداء النقطي للشعاع مع نفسه = الطول2. اكتشاف تعامد شعاعين: حيث يكون الجداء النقطي لشعاعين متعامدين = 0. تساوي الزاوية بين الشعاع ونفسه 0 درجة في الحالة الأولى، وتساوي الزاوية بين الشعاعين 90 درجة في الحالة الثانية، وبالتالي يمكن القول أن الزاوية بين الشعاعين لها علاقة بالجداء النقطي، إذ قد يكون حاصل الجداء النقطي كبيرًا عندما تكون الزاوية بين الشعاعين قريبة من الصفر وصغيرًا عندما تكون الزاوية بينهما قريبة من الزاوية القائمة. سنناقش في هذا المقال المواضيع التالية: الخاصيتان المتعلقتان بالجداء النقطي للأشعة. صيغة لحساب الزاوية بين شعاعي وحدة Unit Vectors. عدد الأشعة التي تبعد عن شعاع معين بالمقدار الزاوي نفسه. معنى جيب التمام السالب للزاوية بين شعاعين. كيفية العثور على الزاوية بين الأشعة التي ليست أشعة وحدة. تأثير طول الأشعة على الجداء النقطي لنفكّر حاليًا في الأشعة في فضاء ثنائي الأبعاد مثل الشعاع a في الرسم البياني السابق، حيث يُحتمَل أن يكون جداؤه النقطي مع الشعاع c الذي له منحى Orientation مقداره 60 درجة أكبر من جدائه النقطي مع الشعاع b الذي له منحى مقداره 30 درجة، لأن الشعاع c أطول بكثير من الشعاع b، ولنتأكد الآن من ذلك الآن. ولتكن لدينا الأشعة التالية: a = (6, 0)T b = (3, 2)T c = (5, 9)T ويكون الجداء النقطي لها هو: a · b = 18.0 a · c = 30.00 توجد خاصيتان متعلقتان بحاصل جداء الأشعة النقطي كما ذكرنا سابقًا وهما: الزاوية بين أشعة الإدخال. طول أشعة الإدخال. ولكننا نرغب الآن في إبقاء تأثير الزاوية فقط من خلال إزالة تأثير الطول بطريقة أو بأخرى، ويمكننا إزالة تأثير الطول باستخدام توحيد Normalize الأشعة، أي إنشاء أشعة الوحدة Unit Vectors في الاتجاه نفسه كما سنوضح في الفقرة التالية. توحيد الأشعة يوضّح الرسم البياني السابق كل شعاع بعد توحيده، أي إنشاء شعاع وحدة باتجاه الشعاع الأصلي نفسه. ملاحظة: تذكّر أن الحرف u المنخفض يشير إلى شعاع الوحدة: ‎bu‎. إلغاء تأثير الطول على جداء الأشعة النقطي لنتأكد الآن من الجداء النقطي الأكبر من بين الجداءين ‎au · bu‎ و ‎au · cu‎ بعد أن وحّدنا الأشعة لإلغاء تأثير الطول على الجداء النقطي. بما أن: u · v = | u | | v | cos θ، وجميع الأشعة طولها يساوي 1.0، فإن الجداء النقطي ‎u · v = cos θ، وبالتالي فإن الجداء النقطي ‎au · bu‎ يساوي جيب تمام الزاوية بين الشعاعين ‎au‎ و ‎bu‎، والذي يمكن قراءته من الرسم البياني على أنه 0.866، بينما يساوي الجداء النقطي ‎au · cu‎ جيب تمام الزاوية بين ‎au‎ و ‎cu‎، والذي يمكن قراءته من الرسم البياني على أنه 0.500. منحى الشعاع ‎bu‎ أقرب إلى الشعاع ‎au‎، لذلك يكون ‎au · bu‎ هو الأكبر حيث: au = (1, 0): شعاع الوحدة عند الزاوية صفر درجة bu = (0.866, 0.5): شعاع الوحدة عند الزاوية 30 درجة cu = (0.5, 0.866): شعاع الوحدة عند الزاوية 60 درجة تذكر أن: cos 30 = 0.866 و sin 30 = 0.5 و cos 60 = 0.5 و sin 60 = 0.866. وبالتالي فإن الجداء النقطي هو: au · bu = 0.866 au · cu = 0.500 لذا يمكن إزالة تأثير الطول باستخدام أشعة طولها 1، ويكون حاصل الجداء النقطي أكبر عندما تفصل زاوية صغيرة بين الأشعة، وإذا كانت الأشعة في اتجاهات متعاكسة مثل ‎(1, 0)T‎ و ‎(-1, 0)T‎، فسيكون مقدار الجداء النقطي سالبًا. مجال قيمة الجداء النقطي لشعاعي وحدة سنوضّح فيما يلي عينة لشعاع الوحدة ‎bu‎ وحاصل الجداء النقطي له مع الشعاع ‎au = (1.0, 0)T‎ لزوايا مختلفة: الزاوية الشعاع b النتيجة صورة توضيحية الزاوية 000 درجة ‎(1.000, 0.000)T‎ تساوي 1.000 الزاوية 015 درجة ‎(0.966, 0.259)T‎ تساوي 0.966 الزاوية 030 درجة ‎(0.866, 0.500)T‎ تساوي 0.866 الزاوية 045 درجة ‎(0.707, 0.707)T‎ تساوي 0.707 الزاوية 060 درجة ‎(0.500, 0.866)T‎ تساوي 0.500 الزاوية 075 درجة ‎(0.259, 0.966)T‎ تساوي 0.259 الزاوية 090 درجة ‎(0.000, 1.000)T‎ تساوي 0.000 الزاوية 105 درجة ‎(-0.259, 0.966)T‎ تساوي ‎-0.259 ‫ الزاوية 120 درجة ‎(-0.500, 0.866)T‎ تساوي ‎-0.500 ‫ الزاوية 135 درجة ‎(-0.707, 0.707)T‎ تساوي ‎-0.707 ‫ الزاوية 150 درجة ‎(-0.866, 0.500)T‎ تساوي ‎-0.866 ‫ الزاوية 165 درجة ‎(-0.966, 0.259)T‎ تساوي ‎-0.966 ‫ الزاوية 180 درجة ‎(-1.000, 0.000)T‎ تساوي ‎-1.000 ‫ ‎bu‎ هو شعاع الوحدة الذي تمثله المصفوفة ‎(cos θ, sin θ )T‎ في كل حالة من الحالات. إذًا مجال قيم حاصل الجداء النقطي لشعاعي الوحدة ‎au · bu‎ هو ‎-1.0 … 1.0. صيغة حساب الزاوية بين شعاعين مجال قيم حاصل الجداء النقطي لشعاعي الوحدة ‎au · bu‎ هو ‎-1.0 … 1.0، لأن كل جداء نقطي في الفقرة السابقة هو: ‎(1, 0)T · ( cos θ, sin θ)T = cos θ وهذا صحيح، فعندما يكون ‎au‎ شعاع وحدة فإنه سيؤشر إلى أيّ اتجاه، وبالتالي يمكن حساب الزاوية بين شعاعي الوحدة كما يلي: au · bu = cos θ‎ حيث θ هي الزاوية بين الشعاعين، وتتضمن هذه الصيغة تلقائيًا حقيقة أن الجداء النقطي للأشعة المتعامدة هو صفر، لأن جيب تمام cos الزاوية 90 يساوي الصفر. أوجد جيب تمام الزاوية بين شعاعي الوحدة اللذين تمثلهما المصفوفتان ‎(0.7071, 0.7071)T‎ و ‎(0.5, 0.866)T‎: cos θ = (0.7071, 0.7071)T · (0.5, 0.866)T = 0.7071 · 0.5 + 0.7071 · 0.866 = 0.9659‎ تدريب عملي تدريب 1: يوضّح الرسم البياني السابق شعاعين هما: الشعاع الأول ‎(0.7071, 0.7071)T‎ وهو شعاع وحدة عند الزاوية 45 درجة، والشعاع الثاني ‎(0.5, 0.866)T‎ وهو شعاع وحدة عند الزاوية 60 درجة، وبالتالي يجب أن يكون حاصل الجداء النقطي لهما هو جيب تمام الزاوية 15. لنوضّح ذلك باستخدام الرموز كما يلي: الشعاع الأول هو ‎(cos 45, sin 45)T‎. الشعاع الثاني هو ‎(cos 60, sin 60)T‎. حاصل الجداء النقطي لهما هو: cos 45 cos 60 + sin 45 sin 60 ‎= cos 45 cos(45 + 15) + sin 45 sin(45+15)‎ ‎= cos 45 (cos 45 cos 15 - sin 45 sin 15) + sin 45 (cos 45 sin 15 + cos 15 sin45)‎ ‎= cos 45 cos 45 cos 15 - cos 45 sin 45 sin 15 + sin 45 cos 45 sin 15 + sin 45 cos 15 sin 45 ‎= cos2 45 cos 15 + sin245 cos 15 ‎= (cos245 + sin245)cos15 ‎= cos 15 استخدامنا في الخطوة رقم 5 القاعدتين التاليتين: cos(x+y) = cos(x) cos(y) - sin(x) sin(y)‎ sin(x+y) = sin(x) cos(y) + cos(x) sin(y)‎ واستخدامنا في الخطوة رقم 9 القاعدة التالية: sin2x + cos2x = 1‎ أوجد جيب تمام Cosine الزاوية بين شعاعي الوحدة المُمثَّلان بالمصفوفتين ‎‎qu = (0.0, 1)T‎ و ‎ru = (0.5, 0.866)T‎: qu · ru = cos θ = 0.866‎ وبالتالي: θ =‫ arc cos 0.866 ‫= 30 درجة. تدريب 2: يظهِر الشكل التالي الشعاعان ‎qu‎ و ‎ru‎ والزاوية بينهما: تذكّر أن: qu · ru = ru · qu‎ يجب أن تكون الزاوية بين الشعاعين 180 درجة أو أقل (حسب التعريف)، ولا يهم ترتيب الأشعة في الجداء النقطي. ملاحظة: من المفيد في بعض الأحيان رسم صورة للتأكد من أن إجابتك منطقية خاصةً عندما تؤشر الأشعة إلى أرباع مختلفة. أوجد جيب تمام الزاوية بين شعاعي الوحدة المُمثَّلان بالمصفوفتين ‎qu = (0.0, 1)T‎ و ‎wu = (-0.5, 0.866)T‎: cos x =‫ 0.866، إذًا يجب أن تكون x =‫ arc cos 0.866 =‫ 30 درجة. لاحظ أن كلا الشعاعين ‎ru‎ و ‎wu‎ يعطيان الإجابة cos 30 عند تطبيق الجداء النقطي عليهما مع الشعاع ‎qu‎، بالرغم من أنهما يقعان على جانبي هذا الشعاع. يوجد شعاعا وحدة يبعدان بمقدار 30 درجة عن الشعاع المعطَى في الفضاء ثنائي الأبعاد، وسيعطي كلاهما النتيجة نفسها للجداء النقطي مع الشعاع المُعطى، لذا يجب أن تكون حذرًا في رسم الأشعة في الحالات الغامضة. الزوايا بين شعاعين التي تكون أكبر من 90 درجة أوجد جيب تمام الزاوية بين شعاعي الوحدة المُمثَّلين بالمصفوفتين ‎qu = (0.0, 1)T‎ و ‎zu = (-0.5, -0.866)T‎: الزاوية بين هذين الشعاعين أكبر من 90 درجة، وبالتالي فإن جيب تمام الزاوية بينهما سالبة، حيث cos θ =‫ ‎-0.866، لأن: θ = arc cos -0.866 = 150‎ الزاوية نفسها تعطي الجداء النقطي نفسه لنحاول الآن رسم الشعاع الآخر الذي جداؤه النقطي مع الشعاع ‎qu‎ يساوي ‎-0.866 كما يلي: الشعاعان اللذان يكون ناتج الجداء النقطي لهما مع الشعاع ‎qu = (0.0, 1)T‎ يساوي ‎-0.866 هما: zu = (-0.5, -0.866)T vu = (0.5, -0.866)T‎ وضعنا في الرسم البياني السابق ذيل هذين الشعاعين عند نقطة الأصل، ولكن تذكّر أن الأشعة ليست ثابتة في أي موقع معين ويمكن رسمها في أيّ مكان مناسب، وأن الجداء النقطي يعطي الزاوية بين منحى كلٍّ من هذين الشعاعين. أوجد الزاوية بين الشعاعين: ‎du = 0.7071(1,1)T‎ و ‎eu = -0.7071(1,1)T‎، وارسم هذين الشعاعين لتوضيح الحالة: 0.7071‎(1, 1)T · -0.7071(1, 1)T = 0.7071(-0.7071)(1+1) = -0.70712 * 2 = -0.5*2 = 1 إذًا الزاوية هي: cos( -1 )‎ =‫ 180 درجة، حيث يوجد شعاع واحد فقط يبعد 180 درجة عن الشعاع المعطى. تدريب عملي أكثر واقعية نادرًا ما يمنحك العالم الحقيقي زوايا سهلة تبلغ 30 درجة و 45 درجة و 60 درجة وما إلى ذلك، لذا إليك تدريبًا أكثر واقعية. أوجد الزاوية المحصورة بين الشعاعين: fu = (0.6, 0.8)T gu = (0.8, 0.6)T قد ترغب أولًا في التأكد من أن هذه الأشعة هي أشعة وحدة فعلًا، لذا ارسم هذه الشعاعين، ثم احسب ناتج الجداء النقطي لهما، واستخدم الدالة arc cos في الآلة الحاسبة لحاسوبك (أو الآلة الحاسبة الحقيقية) للعثور على الزاوية، ولا تنسَ حساب الإجابة بالدرجات وليس بالراديان كما يلي: ناتج الجداء النقطي هو: ‎( 0.6, 0.8 ) · ( 0.8, 0.6 ) = 0.6*0.8 + 0.8*0.6 = 0.48 + 0.48 = 0.96 والزاوية بينهما هي: arc cos( 0.96 )‎ =‫ 16.26 درجة. الأشعة التي ليست أشعة وحدة ليكن لدينا الشعاعان التاليان، ونريد إيجاد الزاوية المحصورة بينهما: j = (3, 4)T k = (0, 2)T نلاحظ أن هذه الأشعة ليست أشعة وحدة، وبالتالي لا يمكنك العثور على الزاوية بينهما دون مزيد من العمل، لذا دعونا نرسم رسمًا بيانيًا لهما أولًا. يمكننا إيجاد الزاوية بين هذين الشعاعين من خلال توحيد Normalize كل منهما وهذا لا يغير منحاهما، وبالتالي أصبح لدينا الآن شعاعا وحدة ويمكن إيجاد جيب تمام الزاوية بينهما باستخدام الجداء النقطي. الزاوية بين الأشعة التي ليست أشعة وحدة لنوجد الآن الزاوية بين الشعاعين j و k: نوجد أولًا طول كل شعاع: | j | = 5.0 | k | = 2.0 ثم نوحّد كلًا منهما، ولكن تذكّر أنه من الحكمة عدم إجراء عملية القسمة في هذه الخطوة في كثير من الأحيان: ju = (3, 4)T / 5.0‎ ku = (0, 2)T / 2.0‎ نحسب الآن الجداء النقطي لهما: ju · ku = (3, 4)T / 5.0 · (0, 2)T / 2.0 = (1/10)(3, 4)T · (0, 2)T = (0.1)(8) = 0.8‎ أخيرًا، نستخدم دالة arc cos في الآلة الحاسبة: arc cos 0.8 = 36.87 درجة لنحسب الآن الزاوية المحصورة بين الشعاعين: ‎a = (10, 5)T‎ و ‎b = (8,12)T‎ مثلًا. نحسب الأطوال أولًا: | a | = √125 | b | = √208 ثم نحسب الجداء النقطي: ‎(10, 5)T / √125 · (8, 12)T / √208 = (108 + 512) / ( √125 √208) = 140 / ( √125 √208) = 140 / √(125*208) = 140 / √26000 = 0.86824 وبالتالي فإن الزاوية هي: arc cos ( 0.86824 ) = 29.745 درجة وصلنا إلى نهاية هذا المقال الذي يحتوي على قدرٍ كبير من الحسابات لإيجاد الزاوية بين شعاعين في فضاء ثنائي الأبعاد، وسنتعرّف في المقال التالي على كيفية إيجاد الزاوية بين شعاعين في فضاء ثلاثي الأبعاد. ترجمة -وبتصرُّف- للفصل The Angle between Two Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: الجداء النقطي وارتباطه بطول الأشعة وتعامدها في التصاميم 3D تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد خاصية الطول Length للأشعة الهندسية في التصاميم ثلاثية الأبعاد

سنوضّح في هذا المقال حقيقتين مهمتين، أولهما أن الجداء النقطي لمصفوفة عمودية مع نفسها يعطي مربع طول الشعاع الذي تمثله، وثانيهما أن الجداء النقطي لمصفوفتين عموديتين تمثلان شعاعين متعامدين يساوي الصفر. سنوضح في هذا المقال المواضيع التالية: الجداء النقطي وطول الشعاع. شعاع الوحدة Unit Vector. شعاع الوحدة الناظم Unit Normal. الجداء النقطي للأشعة المتعامدة ومصفوفاتها العمودية. كيفية بناء شعاع متعامد مع شعاع معين. تعريف ميل Slope الخط ثنائي الأبعاد. العلاقة بين ميول الخطوط المتعامدة ثنائية الأبعاد. صيغة الجداء النقطي المتعلقة بطول الشعاع لنفترض أن لدينا ‎v = ( 3, 4 )T‎، فأوجد ناتج الجداء النقطي v · v وطول الشعاع v: ‎v · v = ( 3, 4 )T · ( 3, 4 )T = 32 + 42 = 9 + 16 = 25 = 52‎ طول v ‫= 5 لأنه جزء من المثلث قائم الزاوية 3/4/5. رأينا في المقال السابق أن الجداء النقطي لشعاع مع نفسه هو: ‎(x, y, z)‎T · (x, y, z)T = x2 + y2 + z2 وتوجد طريقة أخرى لكتابة ذلك وهي: v · v = | v |2‎ ناتج الجداء النقطي لمصفوفة عمودية مع نفسها هو عدد حقيقي (مقدار سلمي) Scalar، وهو مربع طول الشعاع الذي تمثله. ملاحظة: إذا استخدمتَ الإحداثيات المتجانسة Homogeneous Coordinates، فستحتاج هذه العملية الحسابية إلى التعديل بعض الشيء، وتذكّر أن الطول هو خاصية للشعاع الهندسي، وليس خاصية للمصفوفة العمودية التي يمكن استخدامها لتمثيل الشعاع. لنوجد الآن طول الشعاع الذي تمثله المصفوفة العمودية ‎( 2, 1, -1)T‎: ناتج الجداء النقطي هو 4+1+1 = 6، وبالتالي فإن الطول هو ‎√6. خاصيات الجداء النقطي المتعلقة بطول الشعاع إليك بعض الخاصيات الجداء النقطي المتعلقة بطول الشعاع: إذا غيّرتَ حجم شعاع أو ضربته مع عدد حقيقي k، فإنك تضرب طوله بهذه القيمة k: ‎(kv)·(kv) = k2 v 2 وبالتالي | k v | = k| v | طول الشعاع الصفري هو صفر: ‎| 0 | = 0 ناتج الجداء النقطي للشعاع الصفري مع أي شعاع آخر هو صفر: 0‎ · v = 0 لا يغيّر عكس اتجاه الشعاع من طوله: | -v | = | v | أوجد طول الشعاع ‎(30, 40)T‎: ‎(30, 40)T = 10(3, 4)T‎، وبالتالي يكون الطول 10*5 = 50. أو يمكنك حسابه بطريقة أصعب كما يلي: ‎|(30,40)|2 = 900 + 1600 = 2500 والطول = ‎√2500 ‫= 50 أشعة الوحدة Unit Vectors تذكّر أن شعاع الوحدة هو شعاع بطول 1، وتسمَّى عملية إنشاء شعاع وحدة له اتجاه الشعاع المُعطَى نفسه بالتوحيد Normalizing التي تُعطَى بالصيغة التالية (كما ناقشنا في مقال سابق): vu = v / | v | تُطبَّق هذه الصيغة على الأشعة والمصفوفات العمودية التي تمثلها، إذ يمكن حساب الطول | v | باستخدام الجداء النقطي للمصفوفات العمودية. ملاحظة: لاحظ أننا استخدمنا مصطلح "Normal" ، ولكن يجب الانتباه إلى أن لها معانٍ متعددة، إذ يعني مصطلح التوحيد Normalizing إنشاءُ شعاع الوحدة في اتجاه الشعاع الأصلي نفسه، بينما يُطلَق على الشعاع العمودي على سطح معين أحيانًا اسم "الشعاع الناظم Normal Vector"، ولكنه ليس شعاع الوحدة بالضرورة، لذا احرص على ألّا تقول أبدًا "الشعاع الناظم" عندما تقصد "شعاع الوحدة". إبقاء طول الشعاع صريحًا عند حساب شعاع الوحدة جرّب إجراء عملية التوحيد للشعاع الذي تمثله المصفوفة العمودية ‎( 1.2, -4.2, 3.5 )T‎: ناتج الجداء النقطي هو: ‎( 1.2, -4.2, 3.5 )T · ( 1.2, -4.2, 3.5 )T = 1.22 + (-4.2)2 + 3.52 = 31.33 ونمثّل شعاع الوحدة كما يلي: ‎( 1.2, -4.2, 3.5 )T / √31.33. = (0.2144, -0.7504, 0.6253)T يجب عليك ترك الإجابة بالصيغة الأولى السابقة دون إجراء عملية القسمة عند الحل بالورقة والقلم، إذ ستوفر لك الحسابات اللاحقة التي ستجريها في كثير من الأحيان فرصة لإلغاء الطول، إذا تركته صريحًا كما في الصيغة الأولى. تمثيل أشعة الوحدة للاتجاه أجب عن الاسئلة التالية (قد ترغب في التفكير في الأشعة ثنائية الأبعاد أثناء إجابتك، بالرغم من أن الإجابات ستكون صحيحة بالنسبة للأشعة ثلاثية الأبعاد أيضًا): كم عدد الأشعة التي يمكن أن تكون في اتجاه معين؟ متعددة بصورة لا نهائية. كم عدد أشعة الوحدة التي يمكن أن توجد في اتجاه معين؟ شعاع واحد فقط. يمكن أن يكون هناك عدد لا نهائي من الأشعة في اتجاه معين لأن عناصر الشعاع هي أعداد حقيقية، لذلك يوجد عدد لا نهائي من الأشعة التي تحاذي المحور x في الفضاء ثنائي الأبعاد مثلًا، وتبدو المصفوفات العمودية لهذه الأشعة بالصورة ‎(s, 0)T‎. يؤشّر شعاع الوحدة لشعاع معين إلى اتجاه هذا الشعاع نفسه، ولا يوجد سوى شعاع وحدة واحد فقط في اتجاه معين، وتوجد قيمة واحدة فقط للتعبير ‎v / | v |‎، ويوجد شعاع وحدة واحد فقط في اتجاه x الموجب، وتمثله المصفوفة العمودية ‎( +1, 0)T‎. ينطبق الشيء نفسه على المناحي Orientations والأبعاد الأخرى. يظهِر الشكل التالي أشعة لها أطوال مختلفة والمنحى نفسه، ولكن يكون أحدها فقط هو شعاع الوحدة. تذكّر الصيغة التالية لحساب زاوية الشعاع: الزاوية = arc tan( y/x )‎ ولكن ليست هذه الصيغة مفيدة جدًا في الفضاء ثلاثي الأبعاد، إذ لا يكفي تحديد الزاوية بين الشعاع وأحد المحاور فقط عندما يكون هناك ثلاثة محاور. يُستخدَم شعاع الوحدة لشعاع معين في أغلب الأحيان للتعبير عن اتجاه هذا الشعاع، حيث يوجد شعاع وحدة واحد فقط، لذا فإن تعبيره عن الاتجاه فريد من نوعه، وينطبق الشيء نفسه على جميع الأبعاد. ليكن لدينا الشعاع ‎v = ( -3, 2, 4)T‎ مثلًا، حيث يمكننا معرفة اتجاهه من خلال حساب شعاع الوحدة كما يلي: v| v |2 = 9 + 4 + 16 = 29 ‎vu = v / √29 الجداء النقطي للأشعة التي بينهما زاوية قائمة إذا كان لدينا شعاعان موجَّهان بحيث يكون بينهما زاوية مقدارها 90 درجة مثل أن يكون أحدهما يحاذي المحور x والآخر يحاذي المحور y كما في الشكل التالي، فستكون نتيجة جدائهما النقطي هي 0: إذًا لنوجد الجداء النقطي للشعاعين ‎r = (6, 0)T‎ و ‎s = (0, 😎T‎ كما يلي: ‎(6, 0)T · (0, 😎T = 6*0 + 0*8 = 0 لنفترض أننا دوّرنا الشعاعين السابقين بزاوية 45 درجة كما في الشكل السابق ليصبحا كما يلي (لا تقلق بشأن كيفية تدوير الأشعة، إذ سنوضّحه في مقال لاحق): r' = ( 6cos(45), 6sin(45) )T s' = ( -8sin(45), 8cos(45) )T ستبقى الزاوية بينهما بعد تدويرها تساوي 90 درجة، وبالتالي سيكون الجداء النقطي لهما 0 أيضًا. أوجد الجداء النقطي للشعاعين: r' = ( 2cos(45), 2sin(45) )T s' = ( -3sin(45), 3cos(45) )T نطبّق الجداء النقطي كما يلي: r' · s' = 2cos(45) * (-3)sin(45) + 2sin(45) * 3cos(45) = -2cos(45) * (3)sin(45) + 2sin(45) * 3cos(45) = -6cos(45) * sin(45) + 6cos(45) * sin(45) = 0‎ الجداء النقطي للأشعة المتعامدة يبدو من المعقول أن يكون حاصل الجداء النقطي لشعاعين هو نفسه بعد تدويرهما بالمقدار نفسه، وبالتالي نستنتج أن الجداء النقطي لشعاعين متعامدين هو صفر، أي أن الجداء النقطي للمصفوفتين العموديتين اللتين تمثلهما هو الصفر. يهمنا فقط المنحى النسبي، حيث إذا كان الشعاعان متعامدين، فسيكون حاصل الجداء النقطي لهما صفرًا، بغض النظر إن تقاطعا أم لا، إذ ليس من الضروري أن يتقاطع شعاعان ليكونا متعامدين، فمن غير المنطقي التحدث عن تقاطع شعاعين بما أن الأشعة ليس لها موقع محدد، وهذه هي النتيجة نفسها التي رأيناها مع الأشعة الهندسية. يمكننا القول أن الشعاعين التاليين متعامدان لأن حاصل الجداء النقطي لهما يساوي الصفر: q = ( -5, 3 )T‎ r = ( 3, 5 )T عدم اعتماد الجداء النقطي للأشعة المتعامدة على الطول يمكننا تشكيل مصفوفة عمودية ثنائية الأبعاد متعامدة مع مصفوفة أخرى من خلال تبديل العناصر وتغيير إشارة أحدها، ولكن تعمل هذه الطريقة فقط في الفضاء ثنائي الأبعاد، حيث يمكنك العثور على عدد لا حصر له من الأشعة المتعامدة مع شعاع محدَّد مثل الأشعة التالية المتعامدة مع الشعاع ‎( -5, 3)T‎: ( 3, 5 )T ( -3, -5)T ( 1.5, 2.5)T +( 6, 10)T …. وغيرها إذا كان الشعاع u متعامدًا مع الشعاع v، فإن الجداء النقطي ‎u · v = 0، وبالتالي ‎(k u) · v = k(u · v)= 0 لأي عدد حقيقي k، إذًا هناك عدد لا نهائي من الأشعة (k u‎) المتعامدة مع الشعاع v. قد نرغب في العثور على شعاع الوحدة الناظم Unit Normal لشعاع معين الذي هو شعاع: متعامد (ناظم) مع الشعاع المعطى. يبلغ طوله 1. ملاحظة: تذكر ألّا تخلط بين مفهومي التوحيد Normalizing (إنشاء شعاع وحدة في اتجاه الشعاع نفسه)، وحساب شعاع الوحدة الناظم (جعل شعاع الوحدة في اتجاه متعامد مع الشعاع). لنحسب الآن شعاع الوحدة الناظم للشعاع ‎(-5, 3)T‎: ‎(3, 5)/( √34)‎‎، أو يمكنك اختيار الخيار الآخر: ‎(-3, -5)/( √34)‎. عدد لا نهائي من الأشعة الناظمة الأشعة في الفضاء ثلاثي الأبعاد لها أيضًا أشعة وحدة ناظمة، ولكن لا يُعَد شعاع الوحدة الناظم لشعاع معين فريدًا، فمثلًا تكون جميع القضبان متعامدةً مع المحور في عجلة العربة كما في الشكل السابق، أي أنّ جميع الخطوط في مستوي هذه القضبان متعامدة مع المحور، وبالتالي هناك عدد لا نهائي منها. لنوجد عددًا من الأشعة الناظمة للشعاع الذي تمثله المصفوفة العمودية ‎(1, 2, 2)T‎ كما يلي: ( 0, 0, 0 ) ( -2, 1, 0 ) ( 0, -1, 1 ) ( -4, 1, 1 ) ( 0, 1, -1 ) … وغيرها الكثير بعدد لا نهائي جميع الأشعة السابقة هي أشعة ناظمة للشعاع المعطى، لأن حاصل الجداء النقطي لكل منها مع هذا الشعاع يساوي الصفر، ولكنها ليست أشعة وحدة، وإن أردتَ إيجاد أشعة الوحدة الناظمة، فسيكون هناك عدد لا نهائي منها أيضًا. الشعاع الصفري متعامد مع جميع الأشعة لاحظ الشعاع الناظم الأول الذي هو الشعاع الصفري في المثال السابق، فحاصل الجداء النقطي للشعاع الصفري مع الشعاع المُعطَى هو الصفر، لذلك يجب أن يكون الشعاع الصفري متعامدًا مع هذا الشعاع. تستخدم كتب الرياضيات في أغلب الأحيان حقيقة أن الشعاع الصفري متعامد مع جميع الأشعة (من النوع نفسه)، ولكن لن نحتاج إلى هذه الحقيقة حاليًا، بل يمكن أن نحتاجها في المقالات اللاحقة. طول الشعاع الصفري هو صفر، لذا فهو ليس شعاع وحدة ناظم. قد تتذكر من مادة الهندسة التحليلية الصيغة التالية لميل خطٍ في فضاء ثنائي الأبعاد وغير موازٍ للمحور Y: m‎‎ = (التغير في قيمة y) / (التغير في قيمة x) هذه هي الصيغة نفسها المُستخدَمة في ظل الزاوية مع المحور x، وترتبط هذه الصيغة بالسبب الذي يجعل الجداء النقطي للأشعة المتعامدة ثنائية الأبعاد يساوي صفرًا. ميول الخطوط المتعامدة لنحاول الإجابة على الأسئلة التالية: ما هو الميل m1‎ للشعاع ‎( 2, 5 )T‎؟ m1 = 5/2 ما هو الميل m2‎ للشعاع ‎( -5, 2 )T‎؟ m2 = -2/5 ما هو ناتج الجداء النقطي لهما؟ ‎(2)(-5) + (5)(2) = 0 ما هو ناتج ضرب m1‎ و m2‎؟ 5/2‎ * -2/5 = -1 قد تتذكر الحقيقة التالية من دروس الرياضيات السابقة: إذا كان المستقيمان متعامدين فإن حاصل ضرب ميليهما يساوي ‎-1. إليك ما يحدث عندما ننشئ شعاعًا ناظمًا لشعاع ثنائي الأبعاد من خلال تبديل العناصر وتغيير إشارة أحدها: إذا كان ‎v = ( x, y )T‎. فإن الشعاع المعامد له هو ‎v' = ( -y, x )T‎. لأن الجداء النقطي ‎( x, y)T · ( -y, x )T‎ هو ‎-xy + yx = 0. ميل الشعاع ‎( x, y )T‎ هو y/x. ميل ‎( -y, x )T‎ هو ‎-x/y. حاصل ضرب الميلين هو: y/x * -x/y = -(xy)/(xy) = -1. إذًا هل يُعَد الشعاعان ‎( -1.5, 6)T‎ و ‎(2, 2)T‎ متعامدين؟ لا، لأن ناتج الجداء النقطي لهما هو ‎-3 + 12 = 9. ناتج الجداء النقطي ليس صفرًا، لذا فإن الشعاعين ليسا متعامدين، وقد توصّلنا إلى هذه النتيجة بغض النظر عن الأطوال، إذ يمكن اكتشاف تعامد الأشعة بغض النظر عن طولها. وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على علاقة الجداء النقطي للأشعة مع طولها وتعامدها، وسنناقش في المقال التالي الجداء النقطي غير الصفري لشعاعين. ترجمة -وبتصرُّف- للفصل Length and the Dot Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: تطبيق الجداء النقطي Dot Product على الأشعة في التصاميم 3D تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد خاصية الطول Length للأشعة الهندسية في التصاميم ثلاثية الأبعاد

سنتعّرف في هذا المقال على المواضيع التالية: الأسماء المختلفة التي يُعرَف بها الجداء النقطي. تعريف الجداء النقطي للأشعة الهندسية. الخاصية التبديلية للجداء النقطي للأشعة. جيب تمام Cosine الزاوية. الجداء النقطي للأشعة المتعامدة. الجداء النقطي وطول الشعاع. خاصيات الجداء النقطي للأشعة. الجداء النقطي للمصفوفات العمودية ثنائية الأبعاد. الخاصية التبديلية للجداء النقطي للمصفوفات العمودية. الجداء النقطي للمصفوفات العمودية ثلاثية الأبعاد. الجداء النقطي للمصفوفة العمودية مع نفسها. خاصية توزيع الجداء النقطي للمصفوفات العمودية. تعرّفنا حتى الآن على العمليات التالية: ‪| جمع شعاعين | شعاع + شعاع | = | شعاع | | طرح شعاعين | شعاع - شعاع | = | شعاع | | الفرق بين نقطتين | نقطة - نقطة | = | شعاع | | تغيير حجم شعاع (ضرب شعاع بعدد حقيقي) | عدد حقيقي * شعاع | = | شعاع | سنناقش في هذا المقال الجداء النقطي Dot Product الذي يأخذ شعاعين بوصفهما معاملَين وينتج عنه عدد حقيقي بوصفه الخرج. يسمّى الجداء النقطي في بعض الأحيان بالجداء الداخلي Inner Product، ويسمّى أحيانًا أخرى بالجداء السلمي Scalar Product، والذي لا ينبغي الخلط بينه وبين العملية التي تسمى تغيير حجم الشعاع Scaling (ضرب الشعاع بعدد حقيقي). | الجداء النقطي | شعاع . شعاع | = | عدد حقيقي Scalar (مقدار سلمي) | ملاحظة: يُسمى الجداء النقطي أحيانًا بالجداء السلمي، لأنه يأخذ شعاعين وينتج عنه عدد حقيقي Scalar (مقدار سلمي). الزاوية بين شعاعين الزاوية بين الشعاعين u و v هي الزاوية θ التي تكون: 0‪ <= θ <= 180 درجة ويكون ذلك صحيحًا لكل من الفضاء ثنائي الأبعاد وثلاثي الأبعاد، فهذه الزاوية هي أصغر زاوية يمكن أن يدورها أحد الأشعة حتى يحاذي الشعاع الآخر. ولكن إذا كان هناك شعاعان يؤشّران إلى اتجاهين متعاكسين، فستكون الزاوية بينهما تساوي 180 درجة (أو π راديان). الجداء النقطي يكون الجداء النقطي للشعاعين u و v بالنسبة للأشعة الهندسية في الفضاء ثنائي أو ثلاثي الأبعاد هو: u · v = | u | | v | cos θ‪ يُرمَز للجداء النقطي بنقطة بين الشعاعين، ولكن لا تظهِر العديد من المتصفحات النقطة بصورة واضحة لسوء الحظ، إذ قد ترى نقطة صغيرة جدًا أو شريطًا أسود صغيرًا، ويمثّل الرمز θ الزاوية بين هذين الشعاعين. يقع الشعاعان في مستوٍ واحد في الفضاء ثنائي الأبعاد، وبالتالي من السهل تصوّر الزاوية بينهما، بينما يقع الشعاعان في الفضاء ثلاثي الأبعاد في مستوٍ مُضمَّن في هذا الفضاء إلا في الحالة التي يؤشّر فيها الشعاعان إلى الاتجاه نفسه. تكون الزاوية بين الشعاعين صفرًا عندما يؤشّران إلى الاتجاه نفسه وبالتالي: u · v = | u | | v | cos 0 = | u | | v | 1 = | u | | v |‪ بما أن ‎-1 <= cos θ <= +1 فستكون قيمة نتيجة الجداء النقطي بين القيمتين ‎-| u | | v |‎ و ‎+| u | | v |‎ اعتمادًا على الزاوية بين الشعاعين، بينما تكون الزاوية بين الشعاعان 180 درجة وتكون قيمة نتيجة الجداء النقطي هي ‎-| u | | v |‎ عندما يؤشّر هذان الشعاعان إلى اتجاهين متعاكسين. الخاصية التبديلية Commutative للجداء النقطي إذا كان ‎u · v = | u | | v | cos θ، فإن v · u: v · u = | v | | u | cos θ = | u | | v | cos θ = u · v‪‪‪‪ تُعَد عملية الجداء النقطي عملية تبديلية، إذ لا يحدِث ترتيب المعاملات أيّ فرق: ‪u · v = v · u‪ cنوعان مختلفان من الأصفار في المعادلة التالية، إذ تكون معامَلات عملية الجداء النقطي شعاعَين، ويكون خرج العملية قيمة سلمية (عددًا حقيقيًا): 0‪ · 0 = 0‪ يمكن إيجاد a (u · v)‎ حيث "a" عدد حقيقي كما يلي: a (u · v) = a | u | | v | cos θ‪‪ نعيد ترتيب الصيغة السابقة، فينتج: ‪= | a u | | v | cos θ = (a u) · v = u · (a v) جيب تمام Cosine الزاوية 90 درجة قد تكون كيفية عمل دالة جيب التمام Cosine غامضةً إلى حدٍ، لذا تخيّل دائرة الوحدة مع إسقاط نصف قطرها على المحور x كما في الشكل السابق الذي ينتج عنه ما يلي: جيب تمام الزاوية 0 درجة = 1.0 جيب تمام الزاوية 30 درجة = 0.866 جيب تمام الزاوية 45 درجة = 0.707 جيب تمام الزاوية 60 درجة = 0.500 جيب تمام الزاوية 90 درجة = 0.0 وتذكّر أن: u · v = | u | | v | cos θ‪‪‪ الجداء النقطي للأشعة المتعامدة Orthogonal لنفترض أن لدينا شعاعين بينهما زاوية مقدارها 90 درجة، أي أنهما شعاعان متعامدان. هنا يمكن إيجاد جدائهما النقطي كما يلي: u · v = | u | | v | cos 90° = | u | | v | 0.0 = 0.0‪ وبالتالي نستنتج أن الجداء النقطي للأشعة المتعامدة هو صفر، ويمكن تطبيق هذه الحقيقة على الأشعة في جميع الأبعاد. نعني بالشعاعين المتعامدين أن بينهما زاوية مقدارها 90 درجة، ويُعَد الشعاع الصفري متعامدًا مع جميع الأشعة الأخرى، حيث أن ‎0 · v = 0.0 لجميع الأشعة v . كشف التعامد وحساب الطول لنفترض أن الشعاعين s و t ناتج الجداء النقطي لهما يساوي صفر، إذًا: ماذا يمكنك أن تقول عن المنحى النسبي Relative Orientation للشعاعين s و t؟ الشعاعان s و t متعامدان. ماذا يمكنك أن تقول عن طولي الشعاعين s و t؟ لا يمكنك قول أيّ شيء ممّا تعرفه عن الجداء النقطي. إذا كان لدينا شعاعان متعامدان فيما بينهما، فسيكون جداؤها النقطي صفرًا بغض النظر عن أطوالهما، إذ يكتشف الجداء النقطي التعامد بغض النظر عن أطوال الأشعة. ملاحظة: تعتمد إشارة الجداء النقطي لشعاعين u و v على ما إذا كانت الزاوية بينهما حادة أم منفرجة، فإذا كانت قيمة الجداء النقطي صفرًا، فستكون الأشعة متعامدة. لنطّلع الآن على الجداء النقطي للشعاع مع نفسه: v · v = | v | | v | cos 0 = | v | | v | 1.0 = | v |2‪‪ وبالتالي فإن الجداء النقطي للشعاع مع نفسه يساوي مربع طوله. ‪| ‪v | = √(v · v)‪ يحسب الجداءُ النقطي الطولَ باستخدام الصيغة السابقة، وبالتالي يُعَد الجداء النقطي مفيدًا بما أن خاصيتي الشعاع هما الطول والمنحى Orientation، ولكن يمكن أن تتساءل عن إمكانية أن يكون قيمة ‎| ‎v | = √(v · v)‎ سالبة أو صفرًا. حسنًا، لا يمكن أن تكون سالبة، لأن الطول يكون دائمًا صفرًا أو قيمة موجبة، ويكون المقدار ‎| ‎v | = √(v · v)‎ صفرًا عندما يكون الشعاع v هو الشعاع الصفري. خاصيات الجداء النقطي سنسرد فيما يلي قائمة بخاصيات الجداء النقطي وهي: ‎u · v = | u | | v | cos θ: حاصل الجداء النقطي لشعاعين u · v = v · u: الخاصية التبديلية للجداء النقطي لشعاعين ‎u · v = 0 : حيث u و v شعاعين متعامدين 0 · 0 = 0 ‎| v |2 = v · v‎ a (u·v) = (a u) · v‎ ‎u . (v + w ) = (u . v) + (u . w)‎ (v + w ) . u = (v . u) + (w . u) = (u . v) + (u . w) ‎(au + bv) · w = (au) · w + (bv) · w‎: حيث a و b قيم سلمية (أعداد حقيقية) ‎0 . u = 0: حيث 0 (بالخط العريض) هو الشعاع الصفري، و 0 هو عدد‫ حقيقي (مقدار سلمي) ما هو ناتج جداء ‎u · v · w‎؟ ليس للجداء u · v · w معنىً، فإذا كان ‎u · v = a (حيث a عدد حقيقي)، فإن a · w‎ لا معنى له، وإذا كان ‎v · w = b (حيث b عدد حقيقي)، فإن ‎u · b لا معنى له، وليس للتعبير الأصلي أيّ معنًى في كلتا الحالتين. إذًا ما هو ناتج 0‎ · u‎؟ إذا كان "0" (بخط عادي غير عريض) عددًا حقيقيًا، فإن هذه العملية لا معنى لها. إذا كان "0" (بخط عريض) شعاعًا صفريًا، فالنتيجة هي 0 (عدد حقيقي أو مقدار سلمي). الجداء النقطي للمصفوفات العمودية يمكن استخدام الجداء النقطي أيضًا مع المصفوفات العمودية. ليكن لدينا مثلًا المصفوفتان العموديتان التاليتان: a = ( a1, a2 )T‪ b = ( b1, b2 )T فيمكننا تعريف الجداء النقطي لهما على النحو التالي: a · b = a1b1 + a2b2 حيث نضرب العناصر المتقابلة لكل مصفوفة عمودية، ثم نجمع النواتج، وستكون نتيجة الجداء النقطي قيمة عددية (سلمية). ملاحظة: نكتب الجداء النقطي للمصفوفات العمودية في بعض الأحيان على النحو التالي: aT b (مع التعريف نفسه)، وسنوضّح لاحقًا هذه الصيغة الغريبة عند مناقشة ضرب المصفوفات. أوجد ناتج الجداء النقطي للمصفوفتين العموديتين التاليتين: a = ( 1, 2 )T b = ( 3, 4 )T والناتج هو: a · b = 1*3 + 2*4 = 3 + 8 = 11 ولنوجد الآن حاصل جداء b · a كما يلي: b · a = 3*1 + 4*2 = 1*3 + 2*4 = a · b خاصيات الجداء النقطي للمصفوفات العمودية يمتلك الجداء النقطي للمصفوفات العمودية الخاصيات نفسها للجداء النقطي للأشعة، والتي سنوضحها في الفقرات التالية، ولكن لنأخذ أولًا مثالًا لنتعرّف من خلاله على الجداء النقطي للمصفوفات العمودية. لنفترض أن لدينا المصفوفتين العموديتين التاليتين: p = ( -2, 5 )T q = ( 3, -1 )T وسيكون الجداء النقطي لهما هو: p · q = (-2)*3 + 5*( -1) = -6 + -5 = -11‪ وإليك مثال آخر أكثر واقعية: لنفترض أن لدينا المصفوفتين العموديتين التاليتين: s = ( 1.082, -3.224 )T t = ( 2.381, 7.009 )T وسيكون الجداء النقطي لهما هو: s · t = 1.082*2.381 + -3.224*7.009 = 2.576242 + -22.597016 = -20.020774‪ لاحظ أن الجداء النقطي يأخذ معاملين هما مصفوفتان عموديتان وينتج عنه قيمة عددية (سلّمية) واحدة في جميع الحالات. الخاصية التبديلية للجداء النقطي للمصفوفات العمودية لنوجد مثلًا الجداء النقطي للمصفوفتين ‎( -1, 3)T‎ و ‎( 2, 4 )T‎، ثم الجداء النقطي للمصفوفتين ‎( 2, 4 )T‎ و ‎( -1, 3)T‎ كما يلي: ‪( -1, 3)T · ( 2, 4 )T = -12 + 3*4 = -2 + 12 = 10‪ ‪( 2, 4 )T · ( -1, 3)T = 2*(-1) + 4*3 = -2 + 12 = 10 وبالتالي نستنتج أن الجداء النقطي للمصفوفات العمودية هو عملية تبديلية: a · b = b · a لا يشكّل ترتيب المعاملات أيّ فرق كما هو الحال مع الجداء النقطي للأشعة، حيث يمكننا كتابة تعريف الجداء النقطي للمصفوفتين a و b في كلا الترتيبين كما يلي: a · b = ( a1, a2 )T · ( b1, b2 )T = a1b1 + a2b2‪ b · a = ( b1, b2 )T · ( a1, a2 )T = b1a1 + b2a2 = a1b1 + a2b2‪ لاحظ أن الأشياء الموجودة بعد إِشارة المساواة "=" الأخيرة هي نفسها في الحالتين. الجداء النقطي لأنواع المعاملات المختلطة لنفترض أننا نريد إيجاد الجداء النقطي للمصفوفات العمودية a و b و c: a · b · c لكن هذه العملية لا معنى له، إذ ينتج عن الجداء النقطي لشعاعين (أو مصفوفتين عموديتين) عدد حقيقي، ولا يوجد شيء اسمه الجداء النقطي لعدد حقيقي وشعاع (أو مصفوفة عمودية)، فلا معنى للعملية التالية: a · b · c‪ = عدد حقيقي · c أو للعملية التالية: a · b · c = a‪ · عدد حقيقي لذا يجب عليك أن تتابع أنواع المعاملات والنتائج عند التعامل مع الجداء النقطي. لكن العملية التالية لها معنًى (لاحظ أنه لا توجد نقطة بين العدد 2 والشعاع الذي يليه، وهذا يمثّل عملية تغيير الحجم أو ضرب الشعاع بعدد حقيقي Scaling، وليس الجداء النقطي): 2‪( -1, 2)T · ( 4, 1 )T = ( -2, 4)T · ( 4, 1 )T = -2*4 + 4*1 = -8 + 4 = -4 الجداء النقطي في فضاء ثلاثي الأبعاد نعرّف الجداء النقطي لمصفوفات عمودية ثلاثية الأبعاد كما يلي، حيث نضرب العناصر المتقابلة في المصفوفتين ثم نجمع النواتج. ليكن لدينا المصفوفتان العموديتان التاليتان: a = ( a1, a2, a3 )T b = ( b1, b2, b3 )T فيمكننا تعريف الجداء النقطي لهما على النحو التالي: a · b = a1b1 + a2b2 + a3b3 لكن يجب أن تحتوي المصفوفتان العموديتان على عدد العناصر نفسه كما في المثالين التاليين: ‪(1, 2, 3)T · (6, 7, 😎T = 1*6 + 2*7 + 3*8 = 44 ‪( -1, 2, -3)T · (1, -2, 3)T = (-1)(1) + (2)(-2) + (-3)(3) = -1 + -4 + -9 = -14‪ ولا مانع من وجود بعض المتغيرات كعناصر للأشعة كما يلي: ‪(1, 2, 3)T · (x, y, z)T = x + 2y + 3z‪‪ الجداء النقطي مع شعاع صفري جرّب إيجاد ناتج الجداء النقطي للمصفوفتين ‎( 4, 0, -3)T‎ و ‎(0, -2, 0)T‎ كما يلي: ‪‪( 4, 0, -3)T · (0, -2, 0)T = 4*0 + 0*(-2) + (-3)*0 = 0+0+0 = 0 لاحظ أن قيمة طول كل شعاع في الجداء النقطي السابق أكبر من الصفر، ولكن قيمة حاصل الجداء النقطي صفر. إليك مثال آخر: v(0, 0, 0)T · (-2.3, 89.22, 0)T = 0(-2.3) + 0(89.22) + 0(0) = 0‪ ولا يُعَد ذلك مفاجأة، إذ رأينا الخاصية التالية نفسها مع الأشعة الهندسية: 0‪ · a = 0‪ لاحظ أن 0 الأول هو المصفوفة العمودية الصفرية، والصفر الأخير هو العدد الحقيقي صفر، ويمكن أيضًا كتابة ما يلي: 0‪ · 0 = ‪0 تعني المصفوفة العمودية الصفرية في كل من هذه المعادلات مصفوفة عمودية لها بُعد المصفوفة العمودية الأخرى نفسه، وكل عنصر فيها هو العدد الحقيقي صفر. ناتج الجداء النقطي هو جميع القيم الحقيقية الممكنة أوجد ناتج الجداء النقطي للمصفوفتين ‎(-2, 5, -6)T‎ و ‎( 1, 2, 3)T‎: v(-2, 5, -6)T · ( 1, 2, 3)T = (-2)*1 + 5*2 + (-6)*3 = -2 + 10 -18 = -10 لاحظ أن الجواب هو عدد حقيقي سالب، إذ ينتج عن الجداء النقطي جميع أنواع القيم الحقيقية: سالبة وصفر وموجبة، ولكن هناك شيء مهم يحدث عند إجراء عملية الجداء النقطي للشعاع مع نفسه، وهذا ما سنوضّحه في الفقرة التالية. ناتج الجداء النقطي للمصفوفة العمودية مع نفسها هو قيمة موجبة أو صفرية لنوجد مثلًا الجداء النقطي للشعاع ‎(1, -3)T‎ مع نفسه كما يلي: v(1, -3)T · (1, -3)T = (1)(1) + (-3)(-3) = 1 + 9 = 10 يكون ناتج الجداء النقطي للمصفوفة العمودية مع نفسها موجبًا دائمًا كما هو الحال مع الأشعة. ‪(x, y, z)T · (x, y, z)T = x2 + y2 + z2 = قيمة موجبة أو صفرية سيكون مربع x و y و z صفرًا أو أكبر من الصفر بغض النظر عن قيمها، وبالتالي سيكون المجموع صفرًا أو أكبر من الصفر، ولكن المرة الوحيدة التي يكون فيها مربع العدد الحقيقي صفرًا هي عندما يكون هذا العدد الحقيقي صفرًا، لذا فالمرة الوحيدة التي يكون فيها حاصل الجداء النقطي لمصفوفة عمودية مع نفسها صفرًا هي عندما تكون المصفوفة العمودية مصفوفة صفرية. ليكن g شعاعًا ثلاثيّ الأبعاد، فأوجد قيم عناصر هذا الشعاع من خلال حل المعادلة التالية: g · g = 0‪‪ نلاحظ أنه يجب أن يكون كل عنصر من عناصر الشعاع g صفرًا من خلال المناقشة السابقة، لذا: g = 0 = (0, 0, 0)T‪ قابلية توزيع الجداء النقطي على الجمع يمكن توزيع الجداء النقطي على عملية الجمع كما يلي: a · (b + c) = a · b + a · c‪ يبدو هذا جيدًا، ولكن كن حذرًا في تحديد ما تعنيه إشارة "+" على جانبي إشارة المساواة "=". تمثّل إشارة "+" في الجانب الأيسر من المعادلة عملية جمع الأشعة. تمثّل إشارة "+" في الجانب الأيمن من المعادلة عملية جمع الأعداد الحقيقية. من السهل إلى حدٍ ما إثبات أن خاصية التوزيع صحيحة، إذًا لنوضّح هذه الخاصية باستخدام المصفوفات العمودية ثلاثية الأبعاد، بالرغم من أنه يمكن استخدامها مع أيّ بُعد. ويمثّل كلا طرفي المعادلة عددًا حقيقيًا، لذا يجب التحقق من أن هذين الطرفين يمثلان العدد الحقيقي نفسه. إذًا لنبرهن أن ‎a · (b + c) = a · b + a · c‎. ليكن لدينا المصفوفات العمودية التالية: a = (f, g, h)T b = (r, s, t)T c = (x, y, z)T نبدأ بالطرف الأيسر: a · (b + c) = a · ( r+x, s+y, t+z )T = f(r+x) + g(s+y) + h(t+z) = fr + fx + gs + gy + ht + hz‪ ثم بالطرف الأيمن: a · b + a · c = (fr + gs + ht) + (fx + gy + hz) = fr + fx + gs + gy + ht + hz‪ ينتج لدينا أن طرفي المعادلة يمثلان العدد الحقيقي نفسه، ويمكن إجراء الشيء نفسه مع الأشعة بجميع الأبعاد، وبالتالي فإن خاصية التوزيع تكون صحيحة مع جميع الأبعاد. تدريب عملي أوجد ناتج الجداء النقطي التالي: v( -2, 1, 2)T · ( (3, -1, 4)T + ( -2, 1, -2)T ) قد يكون من الأسهل عدم إعادة ترتيب التعبير، بل يُفضَّل إجراء عملية جمع الأشعة أولًا كما يلي: ‪( -2, 1, 2)T · ( (3, -1, 4)T + ( -2, 1, -2)T ) = ( -2, 1, 2)T · (1, 0, 2)T = -2*1 + 1*0 + 2*2 = -2 + 4 = 2 وتكون إعادة ترتيب التعبير أسهل في أحيان أخرى كما في المثال التالي، حيث يكون من الأسهل إجراء عملية الجداء النقطي أولًا: ‪( -2, 0, 2)T · ( (1, -1, 1)T + ( 3, 1, 4)T ) = ( -2, 0, 2)T · (1, -1, 1)T + ( -2, 0, 2)T · ( 3, 1, 4)T = 0 + 2 = 2 خاتمة وضّحنا في هذا المقال مفهوم الجداء النقطي للأشعة وخاصياته، وسنناقش في المقال التالي كيفية ارتباط الجداء النقطي بطول الشعاع. ترجمة -وبتصرُّف- للفصل The Dot Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: تغيير حجم شعاع Scaling في التصاميم ثلاثية الأبعاد 3D خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد خاصية الطول Length للأشعة الهندسية في التصاميم ثلاثية الأبعاد

سنناقش في هذا المقال كيفية جداء الشعاع مععدد حقيقي، حيث تُسمَّى هذه العملية بتغيير الحجم Scaling، وكيفية استخدامها لبناء أشعة الوحدة Unit Vectors التي تُستخدَم لإظهار الاتجاه في الفضاء ثلاثي الأبعاد، وهي ضرورية للرسوميات الحاسوبية ثلاثية الأبعاد. سنوضح في هذا المقال المواضيع التالية: تغيير حجم الشعاع Scaling وخاصياته. معامل تغيير الحجم Scalar. مساواة العناصر المتقابلة في جبر الأشعة. أشعة الوحدة. توحيد Normalizing الأشعة. منحى Orientation شعاع الوحدة. المتغيرات في المعادلات الشعاعية. جداء الشعاع مع عدد حقيقي (تغيير حجم الشعاع Scaling) جرّب معرفة كيفية تعديل عناصر مصفوفة العمودية ‎(3, 4)T‎ بحيث يكون طول الشعاع الذي تمثله ضعف طوله الحالي ويبقى الشعاع يؤشّر إلى الاتجاه نفسه، إذ يمكنك التوصل إلى الإجابة الصحيحة بعناية باستخدام ما تعرفه مسبقًا، أو يمكنك التخمين ثم التحقق من صحة تخمينك كما يلي: 2 × (3, 4)‪T = (6, 😎T لنرى إن كان تخمينك صحيحًا كما يلي: (الطول الجديد)‎2‎ =‏ 62‏ + 82 ‏= 22‏ 32 ‏+ 22‏ 42 ‏= 22‏ (32 + ‏42) =‏ 22 × (الطول القديم)‎2‎. إذًا بأخذ الجذر للطرفين: (الطول الجديد) = 2 × (الطول القديم) ويكون الاتجاه نفسه باستخدام المثلثات المتشابهة، أو يمكنك ملاحظة أن: الاتجاه الجديد = arc tan( 8/6 )‎ ‏= arc tan( 4/3 )‎ = الاتجاه القديم وبالتالي يبدو تخمينك صحيحًا. ملاحظة: يُطلَق على العدد الحقيقي أحيانًا اسم معامل تغيير الحجم (مقدار سلمي) Scalar عند الحديث عن الأشعة. تعني عملية تغيير حجم Scaling الشعاع الهندسي إبقاءَ منحاه Orientation كما هو مع تغيير طوله باستخدام معامل تغيير حجم، إذ تشبه هذه العملية تغيير حجم الصورة، حيث تتوسّع أو تتقلّص الكائنات مع بقاء اتجاهاتها كما كانت سابقًا. إذا كان الشعاع مُمثَّلًا بمصفوفة عمودية ‎(x, y)T‎، فسيؤدي تغيير حجمه وفق عدد معين إلى جداء كل عنصر فيها بهذا العدد كما يلي: a(x, y)T = (ax, ay)T ينطبق ذلك أيضًا على الأشعة ثلاثية الأبعاد، فإذا مثّلنا الشعاع v بالمصفوفة العمودية ‎(x, y, z)T‎، فسيكون تمثيل av‎ بالمصفوفة العمودية ‎(ax, ay, az)T‎. أوجد ناتج ‎0.5×‎(36.4, -18.9)T‎: 0.5×‎(36.4, -18.9)T = (0.5×36.4, 0.5× -18.9)T = ( 18.2, -9.45)T بعض خاصيات عملية تغيير حجم شعاع هناك العديد من خاصيات تغيير حجم الشعاع التي سنوضّحها فيما يلي. الشعاع الذي تغير حجمه هو شعاع أيضا إذا كان v شعاعًا، فإن: ‎-1 ‎v = -v 0‎ v = 0 لاحظ أنه يجب توخي الدقة في العبارتين السابقتين، حيث: ‎-1 v = -v: عدد حقيقي * شعاع = شعاع 0‎ v = 0: عدد حقيقي * شعاع = شعاع نتيجة تغيير حجم شعاع هي شعاع أيضًا، ولاحظ أن 0 بالخط العريض هو شعاع تمثله المصفوفة العمودية ‎(0,0,0)T‎، وليس العدد الحقيقي صفر. التعابير ذات الأنواع المختلطة أوجد ناتج 2‎ + 4‎( 3, 2, 5)T‎: لا يُعَد هذا التعبير صحيحًا، إذ لا يوجد معامل جمع + يطبّق العملية: عدد حقيقي + شعاع لذا من المفيد استخدام الأقواس لإظهار ما تعنيه بالضبط في التعابير التي تحتوي على أنواع ومعاملات مختلطة كما يلي: ‎(2 + 1)(3, -5)T + 4(1, 2)T يمثّل المعامل + الأول عملية جمع لأعداد حقيقية (مقادير سلمية)، ويمثّل المعامل + الثاني عملية جمع لمصفوفات عمودية، لذا يجب تنفيذ العمليات كما يلي: ‎(2 + 1)(3, -5)T + 4(1, 2)T = 3(3, -5)T + 4(1, 2)T = (3×3, 3× -5)T + (4×1, 4×2)T = (9, -15)T + (4, 😎T = (13, -7)T لا يُعَد تطبيق ذلك سيئًا كما يبدو، فما عليك إلّا تتبّع كل معامل وأنواع معامَلاته ونوع نتيجته. لنوجد الآن ناتج ‎-1 (1, 2, -3)T - (2 + 1)(1, 0, 1)T‎: ‎-1 (1, 2, -3)T - (2 + 1)(1, 0, 1)T = ( -1, -2, 3)T - 3(1, 0, 1)T = ( -1, -2, 3)T + (-3, 0, -3)T = (-4, -2, 0 )T جبر الأشعة إذا كان هناك عنصر مجهول أو اثنان في التعبير الذي يحتوي أنواع عمليات مختلطة، فيمكنك استخدام الجبر بالطريقة المعتادة للحل، ولكن كن حذرًا من أنّ كل خطوة تطبّقها تعطي تعبيرًا صالحًا. حل ما يلي مثلًا من أجل a و y: a(1, y)T + 2(0, 5 )T = (2, 20)T قد تقول أنه لا يمكن ذلك بسبب وجود مجهولين (a و y) مع معادلة واحدة فقط، ولكن: a(1, y)T + 2(0, 5)T = (2, 20)T ‎(a, ay)T + (0, 10)T = (2, 20)T ‎(a, ay+10)T = (2, 20)T يجب أن تكون العناصر المتقابلة متساوية، لذا: a = 2 ay + 10 = 20 2y = 10 y = 5 تُعَد هذه الخدعة شائعة وتسمى مساواة العناصر المتقابلة Equating Corresponding Elements. مساواة العناصر المتقابلة لنوجد قيمة x و y فيما يلي: 4‎( -1, y)T + 2( 3x, 10)T = (8, 24)T 4‎( -1, y)T + 2( 3x, 10)T = (8, 24)T ( -4, 4y)T + ( 6x, 20)T = (8, 24)T (6x-4, 4y+20)T = (8, 24)T 6x-4 = 8 4y+20 = 24 6x = 12 x = 2 4y = 4 y = 1 تعني الإشارةُ "=" في المعادلة الأصلية معادلةً شعاعية، بينما تؤدي مساواة العناصر المتقابلة إلى الحصول على معادلتين، حيث تعني الإشارةُ "=" معادلة عددية أو معادلة أعداد حقيقية. تتغير معادلة المصفوفات العمودية إلى عدة معادلات عددية باستخدام مساواة العناصر المتقابلة، حيث يكون لكل بُعد من المصفوفة العمودية معادلة واحدة، ويمكن بعد ذلك حل المعادلات العددية لإيجاد قيمة المجهول في بعض الأحيان وليس دائمًا. إليك مثلًا حالة لا تنجح فيها هذه الطريقة: أوجد قيمة x و y : 4‎(x, 5)T + 2(y, 1)T = 2(12, 11)T قد يبدو كل شيء جيدًا، ولكن يكشف تطبيق بعض الخطوات عن وجود مشكلة كما يلي: 4‎( x, 5)T + 2( y, 1)T = 2(12, 11)T ‎(4x, 20)T + (2y, 2)T = (24, 22)T ‎(4x+2y, 22 )T = (24, 22)T 4x + 2y = 24 22 = 22 لا تحتوي المعادلتان العدديتان اللتان تحصل عليهما من خلال مساواة العناصر المتقابلة على معلومات كافية للمتابعة. لنوجِد الآن قيمة a و x : a( -1, 5 )T + 2( 3x, 10 )T = ( 8, 25 )T يمكن أن نخمن أنه يمكننا إيجاد قيمة a و x كما يلي: a( -1, 5 )T + 2( 3x, 10 )T = ( 8, 25 )T ( -a, 5a)T + ( 6x, 20 )T = ( 8, 25 )T ( 6x-a, 5a+20 )T = ( 8, 25 )T ولنستخدم الآن مساواة العناصر المتقابلة: 6x-a = 8 5a+20 = 25 5a = 5 a = 1 6x-1 = 8 6x = 9 x = 9/6 x = 3/2 تغيير حجم شعاع باستخدام قيم أصغر من واحد نعلم من تعريف عملية تغيير حجم شعاع أنه: a( x, y )T = ( ax, ay )T فلا بأس إن كان a أصغر من واحد، فمثلًا: 0.5‎( x, y )T = ( 0.5x, 0.5y )T يمكن كتابة ذلك في بعض الأحيان على النحو التالي: شعاع الوحدة يبلغ طول الشعاع 1 لأنه محاذٍ للمحور x (في إطار الإحداثيات الحالي)، فالعنصر الوحيد غير الصفري هو 1.0 عند تمثيله بمصفوفة عمودية، ولكن يمكن أيضًا أن يساوي طول الأشعة غير المحاذية لأيّ محور واحدًا، وبالتالي فإن شعاع الوحدة Unit Vector هو شعاع طوله 1. هل يمثل ‎(1, 1, 1)T‎ شعاع وحدة؟ لا، لا يمثل شعاع وحدة لأن طوله لا يساوي 1: ‎√( 12 + 12 + 12 ) = √3 = 1.7320508 إنشاء أشعة الوحدة يبلغ طول أشعة الوحدة 1، وإذا كان لديك شعاع معين v، فيمكنك استخدامه لإنشاء شعاع وحدة، وتسمى هذه العملية بتوحيد الأشعة Normalizing التي تُطبَّق كما يلي: احسب طول الشعاع v وهو | v |. غيّر حجم الشعاع v من خلال تقسيمه على طوله: ‎.v / | v |‎ تُكتَب هذه العملية في كثير من الأحيان بالصيغة التالية (يعني الحرف "u" المنخفض "شعاعَ وحدة Unit Vector"): vu = v / | v |‎ إذا كان ‎v = (x, y, z)T‎، فإن: vu = v / | v | = ( x /| v |, y /| v |, z /| v | )T تستخدم بعض المصادر ترميزًا مختلفًا لذلك، حيث يُستخدَم رمز "القبعة" لأشعة الوحدة î ولكنه لا يظهر جيدًا في المتصفحات، ويسمَّى شعاع الوحدة أحيانًا بالشعاع "المُوحَّد Normalized". جرب توحيد الشعاع ‎(3, 4)T‎ كما يلي: الشعاع هو الوتر في المثلث القائم 3-4-5، وبالتالي فإن طوله هو 5، وشعاع الوحدة هو: 1/5‎ × (3,4)T = (3/5, 4/5)T = (0.6, 0.8)T اتجاه شعاع الوحدة تؤدي عملية تغيير الحجم إلى تغيير طول الشعاع دون تغيير اتجاهه، حيث إذا كان ‎vu‎ هو شعاع الوحدة المقابل للشعاع v، فإن الشعاعين ‎vu‎ و v لهما المنحى نفسه. قد يبدو ذلك مفهومًا، ولكن لنوضّحه أكثر: ابدأ بالشعاع ‎v = (3, 4)T‎. أنشئ شعاع الوحدة ‎vu = (3/5, 4/5)T‎. اتجاه الشعاع v هو arc tan( 4/3 )‎. اتجاه ‎vu‎ هو: arc tan( (4/5) / (3/5) ) = arc tan( (4/5) × (5/3) ) = arc tan( 4/3 ) يمكننا إنشاء شعاع وحدة له اتجاه الشعاع ‎w = (4, 6)T‎ نفسه مثلًا كما يلي: ‎| ‎w | = √(16 + 36) = √52 wu = (4, 6)T / ( √52) ولنتأكد الآن من صحة الإجابة: ‎| wu |T = (4T + 6T) / ( √52)T = (16 + 36)/52 = 52/52 =1.0 ‎| wu | = 1.0 يؤشّر شعاع الوحدة المتشكّل من شعاع ثلاثي الأبعاد إلى اتجاه الشعاع الأصلي نفسه أيضًا، إذًا لنجرّب مثلًا توحيد الشعاع ‎g = (-3, 4, -1)T‎: ‎| g | = √(9 + 16 + 1 ) = √26 gu = (-3, 4, -1)T / (√26) الاتجاه المعاكس يمثل ‎(1, 1)T / (√2)‎ شعاعَ وحدة له منحى مقداره 45 درجة، وطوله ‎√‎( 12/2 + 12/2 ) = 1، وزاويته مقدارها arctan(1/1)‎ =‫ 45 درجة، ولكن يمكنك إنشاء شعاع وحدة يؤشّر في الاتجاه المعاكس لهذا الشعاع من خلال أخذ معاكس كل مكوّن من مكوناته كما يلي: ‎-( 1, 1)T / (√2) = (-1, -1)T / (√2) تدريب: أنشئ شعاع وحدة يؤشّر إلى الاتجاه المعاكس للشعاع ‎(3, 0, 2)T‎: طول الشعاع = ‎√(9+4)‎ ‫= ‎√13 شعاع الوحدة في الاتجاه الأول = ‎(3, 0, 2)T / ( √13)‎ شعاع الوحدة في الاتجاه المعاكس = ‎( -3, 0, -2)T / ( √13)‎ بهذا نكون قد وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على مفهوم تغيير حجم الأشعة وشعاع الوحدة، وسنناقش في المقال التالي الجداء النقطي Dot Product لشعاعين في التصاميم ثلاثية الأبعاد. ترجمة -وبتصرُّف- للفصل Scaling and Unit Vectors من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد كيفية جمع الأشعة الهندسية للتصاميم ثلاثية الأبعاد

يناقش هذا المقال خاصيةً مهمةً أخرى للشعاع وهي خاصية الاتجاه، إذ ناقشنا في المقال السابق خاصية الطول، حيث تعرّف هاتان الخاصيتان الشعاع. سنوضّح في هذا المقال المواضيع التالية: المنحى Orientation أو اتجاه الحركة للأشعة ثنائية الأبعاد (مُمثَّلة في إطار إحداثي معين). الغموض عند استخدام قوس الظل arc tan لحساب الزاوية. تحويل الطول والمنحى إلى مكونات مصفوفة عمودية. قياس الزوايا بوحدتي الراديان Radian والدرجة المئوية. استخدام لغتي البرمجة سي C وجافا Java مع قوس الظل. الأشعة المحاذية للمحورين X-Y ما هو اتجاه الشعاع الذي تمثله المصفوفة العمودية ‎(4, 0)T‎؟ يوازي هذا الشعاع المحور X لإطار الإحداثيات الذي نستخدمه، وسيكون هذا الشعاع غالبًا أفقيًا ويؤشّر إلى اليمين (أو يمكن القول أن الشعاع له منحى مقداره 0 درجة). للشعاع ثنائي الأبعاد الذي يحاذي محور الإحداثيات -كما هو الحال مع ‎(4, 0)T‎- منحًى يسهل رؤيته، ويكون عند 0 درجة أو 90 درجة أو 180 درجة أو 270 درجة. يُعبَّر عن منحى الشعاع عادةً من خلال زاوية مع المحور x الموجب لإطار الإحداثيات، وهناك طريقتان لذلك: تُقاس الزاوية من 0 إلى 360 درجة بعكس اتجاه دوران عقارب الساعة ابتداءً من المحور x الموجب. تُقاس الزاوية من 0 إلى ‎+180 درجة بعكس اتجاه دوران عقارب الساعة, ابتداءً من المحور x الموجب، أو تُقاس من 0 إلى ‎-180 درجة مع اتجاه دوران عقارب الساعة ابتداءً من المحور x الموجب. حساب زاوية الشعاع عن المحور X ما هو اتجاه الشعاع a في المخطط البياني السابق؟ يكون منحى الشعاع a = (4, 4)T‎ بزاوية مقدارها 45 درجة. يجب أن تعطي الرياضيات الإجابة نفسها، إذ يُقدَّر ميل Slope الشعاع a بما يلي: (التغير في قيمة x)/(التغير في قيمة y)‫ = 4.0/4.0 = 1.0 بالتالي تكون الزاوية باستخدام قوس الظل هي: 45‎ = arc tan( 1.0 )‎ درجة. ليس للأشعة موقع، لذا لا يعتمد الطول ولا الاتجاه على المكان الذي ترسم فيه الشعاع، وتكون صيغة اتجاه الشعاع ثنائي الأبعاد هي: angle of (x, y)T = arc tan( y/x ) وللتأكيد يعني استخدام قوس الظل لقيمةٍ ما arc tan( z )‎ أنه تم العثور على الزاوية التي لها ظل tangent مقداره z، وتذكّر -عند حسابها باستخدام الآلة الحاسبة- أن الإجابة يمكن أن تكون بالراديان أو بالدرجات، إذ تمنحك معظم الآلات الحاسبة خيار استخدام أيّ من هذين التنسيقين. وبما أن الآلات الحاسبة تعطي عادةً الإجابة محصورةً بين ‎-90.0 و ‎+90.0 درجة (أو بين ‎-pi و ‎+pi راديان)، فقد تضطر إلى تعديل الإجابة (سنوضح ذلك لاحقًا). يمكنك أيضًا استخدام الآلة الحاسبة على حاسوبك، فإذا كنت تستخدم نظام التشغيل ويندوز، فانقر على الخيار "علمي Scientific" في قائمة "العرض View" للآلة الحاسبة التي تحتوي على قوس الظل arc tan الذي يمكن أن يكون له تسمية هي tan-1‎. ما هو منحى الشعاع الذي تمثله المصفوفة العمودية: ‎k = (3,4)T‎ (باستخدام الآلة الحاسبة)؟ ‪arc tan( y/x ) = arc tan( 4/3 ) = arc tan( 1.333333333333 ) = 53.13 درجة التعامل مع القيم السالبة يوضح المخطط البياني السابق الشعاع الذي تمثله المصفوفة العمودية: ‎k = (3,4)T‎، والذي حسبنا منحاه ليكون 53.13 درجةً عن محور x الموجب، وبالتالي يبدو كل شيء صحيحًا. لنحسب الآن منحى الشعاع ‎-k = (-3,-4)T‎ من خلال استخدام الصيغة التالية: ‪arc tan( y/x ) = arc tan( -4/-3 ) = arc tan( 4/3 ) = arc tan( 1.333333333333 ) = 53.13 درجة لاحظ وجود خطأ، إذ أعطتنا هذه الصيغة الزاوية نفسها للشعاع الذي يؤشّر إلى الاتجاه المعاكس لاتجاه الشعاع الأول. تكمن المشكلة في فقدان المعلومات عند قسمة ‎-4 على ‎-3، إذ لا يمكننا تفريق هذه النتيجة عن نتيجة قسمة ‎+4 على ‎+3، وبالتالي هذه الصيغة ليست كافيةً لتعطيك الإجابة الصحيحة، ويجب عليك رسم الشعاع ثم تعديل الإجابة. لاحظ من المخطط البياني أن منحى الشعاع ‎-k الذي يُعبَّر عنه بالدرجات من 0 إلى 360 بعكس اتجاه عقارب الساعة عن المحور x هو (180 + 53.13) = 233.13 درجة. ما هو منحى الشعاع الذي تمثله المصفوفة العمودية: ‎ p = (3,-4)T‎(استخدم تطبيق الآلة الحاسبة الموجود على حاسوبك)؟ ضع الأعداد في حاسبة ويندوز كما يلي: ‪arc tan( y/x ) = arc tan( -4/3 ) = arc tan( -1.333333333333 ) = -53.13 درجة يبدو الحساب صحيحًا في المخطط البياني السابق، وإذا أردتَ التعبير عن الزاوية بعكس اتجاه دوران عقارب الساعة، فهي 360 - 53.130 = 306.870 درجة، ولكن سيعطيك الشعاع ‎-p النتيجة نفسها للأسف، لذا ارسم دائمًا الشعاع عندما تحسب منحاه، بعدها يمكنك أن ترى أن الزاوية التي تريدها للشعاع ‎-p هي 180 - 53.130 = 126.87 درجة. تتوفر الدالة atan2(y, x)‎ في معظم لغات البرمجة، إذ تحسب هذه الدالة الزاوية بالراديان بين المحور x الموجب والنقطة المعطاة بالإحداثيات (x, y)، وتستخدِم إشارتَي x و y لتحديد الربع الصحيح للزاوية. ما هو منحى الشعاع ‎u = (-4,-2)T‎ ؟ (ارسم الشعاع أولًا، ثم استخدم الآلة الحاسبة)؟ عوّض القيم في الصيغة واستخدم الآلة الحاسبة لإيجاد الناتج: ‪arc tan( y/x ) = arc tan( -2/-4 ) = arc tan( 0.5 ) = 26.565 درجة ولكن سترى عند رسم الشعاع أنه يقع في الربع الخطأ، لذا يجب أن تكون الإجابة 180 + 26.565 = 206.565 درجة. حساب السمتين (x, y) الخاصتين بالشعاع لنفترض أنك تعلم أن الشعاع يمكن تمثيله بمصفوفة عمودية ‎(x, y)T‎ باستخدام إطار إحداثي معين، ويمكن حساب هاتين السمتين x و y كما يلي: ‪orientation of (x, y)T = arc tan( y/x ) ‪|(x, y)T| = √( x2 + y2 ) ارسم الشعاع r الذي تمثله المصفوفة العمودية ‎(4, 5)T‎، ثم قدّر طوله واتجاهه، وأجرِ العمليات الحسابية للحصول على الإجابة الدقيقة كما يلي: الطول: ‪| r | = | (4,5)T | = √(16+25) = 6.40 الاتجاه: ‪direction = arc tan{ 5/4 } = 51.34 درجة تحويل الطول والاتجاه إلى السمتين (x, y) لنفترض أن لديك طول واتجاه وتريد التعبير عنهما بشعاع عمودي ثنائي الأبعاد، يمكنك فعل ذلك باتباع الخطوات التالية: أنشئ مخططًا بيانيًا. احسب قيمة x من خلال إسقاط الطول على المحور x باستخدام length*cos( θ )‎. احسب قيمة y من خلال إسقاط الطول على المحور y باستخدام length*sin( θ )‎. تحقق من الإجابات وفق المخطط البياني. لنفترض أن لدينا شعاعًا طوله 4 ومنحاه بزاويةٍ مقدارها 150 درجة. إذًا ما هي المصفوفة العمودية التي تمثّل هذا الشعاع؟ سنمثّل هذا الشعاع بالمصفوفة العمودية ثنائية الأبعاد ‎( -3.464, 2.0 )T‎ . حساب الزوايا بالراديان اتبع الخطوات التالية في هذا الحساب: أنشئ مخططًا بيانيًا كما يلي: احسب قيمة x من خلال إسقاط الطول على المحور x كما يلي: ‪4 * cos( 150 ) = -3.464 احسب قيمة y من خلال إسقاط الطول على المحور y كما يلي: ‪4 * sin( 150 ) = 2.0 تحقق من الإجابات وفق المخطط البياني (تبدو جيدة). كن حذرًا بشأن استخدام هذه الصيغ وتوقّع الإجابات الصحيحة، خاصةً عند البرمجة بلغة سي أو جافا، إذ يمكن للمكتبات الرياضية الخاصة بلغة البرمجة أن تعطي أشياءً غير متوقعة إن لم تكن حذرًا، ولكن توجد ثلاثة أماكن يجب توخي الحذر فيها بصورة خاصة وهي: من المتوقع أن يكون وسيط sin()‎ و cos()‎ و tan()‎ بالراديان، والقيمة التي تعيدها atan()‎ بالراديان. من المتوقع أن يكون وسيط معظم الدوال الرياضية من النوع double، ولكن إذا استخدمتَ عددًا عشريًا float أو عددًا صحيحًا int، فلن تحصل على رسالة خطأ، بل مجرد إجابة غريبة غير صحيحة. توجد عدة إصدارات من دالة "arc tan" في معظم مكتبات لغة سي، وكلٌ منها مخصَّص لمجال مختلف من قيم الخرج. يُعبَّر عن الزوايا عادةً بالراديان، وتُقاس الزوايا بعكس اتجاه عقارب الساعة ابتداءً من المحور x الموجب (أو تُقاس الزاوية السالبة باتجاه عقارب الساعة ابتداءً من المحور x الموجب أحيانًا)، إذ يوجد ما مقداره 2‎ pi راديان في الدائرة الكاملة، أي أن: (‎(2 pi راديان = 360 درجة لنفترض أن لدينا شعاعًا له طول length وزاوية angle! أوجد في هذه الحالة قيمة vector[0]‎ التي تمثل المركّبة x، وأوجد قيمة vector[1]‎ التي تمثّل المركّبة y الخاصة بهذا الشعاع. #include <math.h> double length, angle; /* طول وزاوية الشعاع */ double vector[2]; /* عناصر الشعاع */ . . . length = قيمةٌ ما angle = عددٌ ما بالدرجات vector[0] = ???? vector[1] = ???? لنفترض أن رمز pi هو M_PI، ولكن لسوء الحظ تستخدم المصرّفات Compilers المختلفة رموز PI مختلفة وتعرّفها في ترويسات ملفات مختلفة، لذا يجب أن تستخدم الرمز المناسب لنظام تشغيلك بدلًا من تعريف PI بنفسك. ملاحظة: إذا لم تكن على دراية بلغة سي، فيمكنك عَدّ هذه الشيفرة بأنها مكتوبة بلغة جافا. #include <math.h> double length, angle; double vector[2]; . . . length = قيمةٌ ما angle = عددٌ ما بالدرجات vector[0] = length * cos( angle*M_PI/180.0 ) vector[1] = length * sin( angle*M_PI/180.0 ) تدريب عملي تذكّر أولًا الخطوات التي يجب اتخاذها لتحويل الشعاع المعلوم طوله واتجاهه إلى (x,y): أنشئ مخططًا بيانيًا. احسب قيمة x من خلال إسقاط الطول على المحور x باستخدام length*cos( θ )‎. احسب قيمة y من خلال إسقاط الطول على المحور y باستخدام length*sin( θ )‎. 4: تحقق من الإجابات وفق المخطط البياني. وتبقى الخطوات نفسها إذا كانت الزاوية مُعطاةً بالراديان. تدريب 1: ليكن لدينا شعاع طوله 4.5 (بأيّ وحدة طول) وزاوية منحاه 0.70 راديان، ولنعبّر عن هذا الشعاع بالصيغة ‎( x, y )T‎ كما يلي: أنشئ مخططًا بيانيًا كما يلي: احسب قيمة x من خلال إسقاط الطول على المحور x كما يلي: ‪4.5*cos( 0.70 ) = 3.442 احسب قيمة y بإسقاط الطول على المحور y كما يلي: ‪4.5*sin( 0.70 ) = 2.899 تحقق من الإجابات وفق المخطط البياني. تدريب 2: لنفترض أن الدعسوقة ليلى أضاعت صديقتها سلوى، ولكن كان مع ليلى هاتف محمول لحسن الحظ وكان: موقع ليلى عند النقطة ‎(1, -4)‎. موقع سلوى عند النقطة ‎( -4, 3)‎. اتصل بليلى وأخبرها في أيّ اتجاه وإلى أيّ مسافة يجب أن تمشي للوصول إلى صديقتها سلوى. الحل: الاتجاه = 125.54 درجة، والمسافة = 8.60. كان عليك أن تتذكر كيفية حساب الإزاحة للحصول على الإجابة، إذ يمكنك حساب شعاع الإزاحة بين نقطتين (أو بين الدعسوقتين) كما يلي: (المكان الذي تريد أن تكون فيه) - (مكانك الحالي) = (الإزاحة التي تحتاجها) إذًا الإزاحة التي يجب أن تمشيها ليلى هي: ‪( -4, 3) - (1, -4) = (-5, 7) ولكن تحتاج ليلى إلى مسافة وجهة هما: المسافة: ‎√(25 + 49) = 8.60 الاتجاه: ‪arc tan( 7/-5 ) = arc tan( -1.4 ) = -54.46 درجة نعدّل الاتجاه بالنظر إلى المخطط البياني ويصبح الاتجاه هو: 180 - 54.46 = 125.54 درجة هل يمكن تطبيق الأفكار المتعلقة بمنحى الشعاع ثنائي الأبعاد الواردة في هذا المقال في الفضاء ثلاثي الأبعاد؟ نعم، ولكن ليس بهذه السهولة، إذ سيتطلب منحى الأشعة ثلاثية الأبعاد مزيدًا من العمل. وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على خاصية الاتجاه الخاصة بالشعاع، وسنناقش في المقال التالي حاصل ضرب شعاع وقيمة عددية. ترجمة -وبتصرُّف- للفصل Vector Direction من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق تعرف على خاصية الطول Length للأشعة الهندسية وكيفية حسابه. المعاملات (parameters) في جافا. الأنواع الحقيقية والصحيحة في لغة سي C.

يناقش هذا المقال طول Length الأشعة وكيفية حساب هذا الطول باستخدام تمثيل المصفوفة العمودية للأشعة، وسنناقش في المقال التالي خاصيةً أخرى للأشعة، وهي خاصية الاتجاه Direction؛ إذ للأشعة بجميع أبعادها خاصيتان هما: الطول والاتجاه، ولكن سنستخدم أشعة في فضاء ثنائي الأبعاد للسهولة. سنوضّح في هذا المقال المواضيع التالية: طول الأشعة ثنائية وثلاثية الأبعاد. صيغة فيثاغورس. حساب طول الشعاع من خلال تمثيله بالمصفوفة العمودية. طول الشعاع الصفري. طول الشعاع السالب. الأشعة المحاذية للمحورين X-Y ما هو طول الشعاع التالي الذي تمثله المصفوفة العمودية ‎(3, 0)T‎؟ يمكن القول أن الطول يساوي 3 وحدات. إذا كان هناك شعاع ثنائي الأبعاد يحاذي المحور x، فإن المصفوفة العمودية التي تمثله لها قيمة غير صفرية في العنصر الأول، وصفر في العنصر الثاني، إذ من السهل تحديد طول الشعاع الأخضر المُمثَّل بالمصفوفة العمودية ‎ (3, 0)T‎في المخطط البياني التالي، فالطول هو قيمة العنصر الوحيد غير الصفري في تلك المصفوفة. يحاذي الشعاع a (الشعاع الأزرق في المخطط البياني السابق) المحور y، ومصفوفته هي ‎(0, 4)T‎، فما هو طول الشعاع a؟ طوله 4 وحدات، إذ يمكن قراءته من المخطط البياني، ولكن ليس للشعاع موقع ثابت طبعًا، لذلك يمكن رسم الشعاع a في أيّ مكان وسيكون له الطول نفسه. صيغة فيثاغورس يوضح المخطط البياني التالي شعاعين بطول 3 و4 مع الشعاع الجديد h: من الصعب معرفة طول الشعاع h، ولكنه ليس صعبًا كثيرًا؛ خاصةً إذا كنت على معرفة بقاعدة "3، 4، 5 في المثلثات قائمة الزاوية"، إذ يمكن ترتيب الأشعة الثلاثة في مثلث قائم الزاوية، بحيث يكون h هو الوتر، والضلعان الآخران هما 3 و 4؛ وبالتالي فإن طول h يساوي 5 باستخدام صيغة فيثاغورس والتي هي: (طول الوتر)2 = (طول الضلع القائمة الأولى)2 + (طول الضلع القائمة الثانية)2 إذا استخدمنا صيغة فيثاغورس مع مثلث قائم الزاوية له ضلعان قائمان طولهما 3 و 4، فسنحصل على طول الوتر كما يلي: ‫(طول الوتر)2 ‫= ‫32 + ‪‫42 ‫ ‫(طول الوتر)2 ‫=‫ ‪‫9 +‫ 16 = 25 (طول الوتر) = 5 إذًا ما هو طول الوتر في المثلث القائم الزاوية الذي طول ضلعيه 6 و 8؟ وما طول الوتر في المثلث القائم الزاوية الذي طول ضلعيه القائمين 6 و 8؟ سنستخدم للحل صيغة فيثاغورس كما يلي: ‫الطول2 ‫= ‪ ‫62 + ‪‫62 ‫ ‫الطول2 ‫= ‪‫36 +‫ 64 = 100 الطول = 10 استخدام صيغة فيثاغورس لحساب طول الأشعة يمكن استخدام صيغة فيثاغورس لحساب طول الشعاع ثنائي الأبعاد. لنفترض أن الشعاع تمثّله المصفوفة العمودية ‎(x, y)T‎، لذا ضع ذيل الشعاع عند نقطة الأصل، ثم أنشئ مثلثًا من خلال رسم الضلعين الآخرين كما في المخطط البياني السابق: side_1 = (x, 0)T side_2 = (0, y)T طول الضلع الأول side_1 هو x، وطول الضلع الثاني side_2 هو y، وبالتالي ينتج لدينا أن الطول: length (x, y)T = √( xT + yT ) يمثّل الرمز √ الجذرَ التربيعي الموجب في هذه الصيغة، إذ لا نريد بالطبع أن يكون الطول سالبًا. ما طول الشعاع الذي تمثله المصفوفة العمودية ‎(4, 3)T‎؟ الطول يساوي 5.0، إذ يمكنك استخدام الصيغة السابقة، أو إدراك أنه مثلث قائم زاوية آخر أطول أضلاعه 3-4-5. الرمز المستخدم لطول الشعاع تعمل صيغة فيثاغورس مع الأشعة المحاذية للمحاور كما يلي: length of( (8,0)T ) = √( 8*8 + 0*0 ) = 8 لا يُعَد الاستمرار في قول "طول ( ) أو length of ( )‎" مناسبًا، لذا يوجد رمزٌ لذلك وهو: طول ‎| a | = ( a )‎ للرمز a شريطٌ عمودي من كل جانب، وتستخدم الكتب أحيانًا شريطين عموديين على كل جانب، وبالتالي تكون الصيغة كما يلي: ‪| (x, y)T | = √( x2 + y2 ) إذا كان ‎g = (1, 1)T‎، فما هو | g | ؟ نعوّض في الصيغة كما يلي: ‪| g | = √( 12 + 12 ) ‪= √2.0 ‪= 1.414213562373 لاحظ أن الطول ليس 1.0 ولا 2.0، وهذا خطأ يقع فيه بعض الأشخاص. إثبات متراجحة المثلث تذكّر أن طول مجموع شعاعين أقل من أو يساوي مجموع طولي هذين الشعاعين: طول ( v + u ) <= طول ( u ) + طول ( v ) وفي الصيغة الجديدة: | u + v | <= | u | + | v | لتكن لدينا الأشعة المُمثَّلة بالمصفوفات العمودية التالية: u = (3, 4)T v = (3, -4)T w = u + v = (6, 0)T يوضّح المخطط البياني التالي كيفية عمل متراجحة المثلث في هذا المثال، إذ يكون مجموع طولي الشعاعين الأحمر والأزرق أقل من طول الشعاع الأخضر. ولكن هل يمكن تطبيق ذلك عدديًا؟ وما هي قيمة كلٍّ من | u | و | v | و | w |؟ إجابة: ‎u = (3, 4)T‎ وبالتالي: ‎| u | = 5 ‎v = (3, -4)T‎ وبالتالي: ‎| v | = 5 ‎w = u + v = (6, 0)T‎ وبالتالي: ‎| w | = 6 طبعًا 6 < 5 + 5 مما يدل على أن: | u + v | <= | u | + | v | تدريب عملي لا تكون عناصر الشعاع عادةً قيمًا صحيحةً بسيطة، ولتكن لدينا مثلًا بعض الأشعة المُمثَّلة بمصفوفات عمودية تحتوي على كسور عشرية في عناصرها كما يلي: q = (2.2, 3.6)T r = (-4.8, -2.2)T s = q + r يمكن طبعًا استخدام صيغة فيثاغورس، ولكنك ستحتاج إلى آلة حاسبة لاستخدامها. ‪| (x, y)T | = √( x2 + y2 ) ما هي أطوال الأشعة q و r و s؟ ‪| q | = √( 2.22.2 + 3.63.6 ) = √( 4.84 + 12.96 ) = √ 17.8 = 4.219 ‪| r | = √( -4.8* -4.8 + -2.2 * -2.2 ) = √( 23.04 + 4.84 ) = √ 27.88 = 5.280 ‪| s | = √( -2.6 * -2.6 + 1.4*1.4 ) = √( 6.76 + 1.96 ) = √ 8.72 = 2.953 يكون | s | أصغر من | q | + | r | كما هو متوقع. حساب طول الأشعة ثلاثية الأبعاد تكون للأشعة ثلاثية الأبعاد خاصية الطول، ويمكن استخدام الصيغة فيثاغورس نفسها لحساب الطول، إذ يكون طول الشعاع الذي تمثله مصفوفة مكونة من ثلاثة مكونات هو: ‪| (x, y, z)T | = √( x2 + y2 + z2) كما في المثال التالي: ‪| (1, 2, 3)T | = √( 12 + 22 + 32 ) = √( 1 + 4 + 9 ) = √14 = 3.742 إذًا لنحسب طول ‎(2, -4, 4)T‎ و ‎(-1, -2, 3)T‎ كما يلي: ‪| (2, -4, 4)T | = √( 2 * 2 + -4 * -4 + 4 * 4) = √( 4+ 16 + 16 ) = √36 = 6 ‪| (-1, -2, 3)T | = √( -1 * -1 + -2 * -2 + 3 * 3) = √( 1 + 4 + 9 ) = √14 = 3.742 يعطي تربيع عناصر الشعاع ناتج جمع للقيم الموجبة (أو الصفرية)، مما يضمن أن يكون الطول قيمة موجبة (أو صفرًا). الأشعة الهندسية ضع في بالك أن الأشعة هي كائنات هندسية، أي يُعبَّر عنها بطولٍ واتجاه في الفضاء. تُمثَّل الأشعة بالمصفوفات العمودية، وتفترض صيغ حساب الطول في هذا المقال استخدام إطار إحداثي وأن الأشعة مُمثَّلة بمصفوفات عمودية ضمن هذا الإطار. يمكن أن يناقش أيّ كتابٍ خاص بالرسوميات الحاسوبية كيفية استخدام الإحداثيات المتجانسة Homogeneous Coordinates لتمثيل الأشعة، إذ تستخدم هذه الطريقة مصفوفات عمودية مكونة من 4 مكونات لتمثيل الأشعة في فضاء ثلاثي الأبعاد، ويتطلب حساب طول الشعاع المُمثَّل بهذه الطريقة تعديل الصيغ، مع تجاهل المكون الرابع للمصفوفة العمودية. لا تقلق بشأن هذه الطريقة حاليًا، إذ سنوضّح التفاصيل لاحقًا، وخذ الوقت الكافي لفهم فكرة أن المصفوفات العمودية التي نستخدمها ليست الطريقة الوحيدة لتمثيل الأشعة، وأن خاصية الطول هي خاصة بالشعاع، وليست خاصة بالمصفوفة العمودية التي تمثل هذا الشعاع، لذا قد تتساءل عن وجود أيّ أهمية لتمييز شيء ما عن تمثيله في علوم الحاسوب! حسنًا، نعم هناك أهمية طبعًا، ويُعَد ذلك من أهم الأفكار في علوم الحاسوب. ليكن لدينًا مثلًا المخطط البياني التالي الذي يحتوي شعاعًا وإطارين للإحداثيات هما: إطار رمادي فاتح وإطار برتقالي. نمثّل الشعاع بالمصفوفة العمودية ‎(8, 6)T‎ في الإطار الرمادي الفاتح، ونمثّله في الإطار البرتقالي بالمصفوفة العمودية ‎(9.8, 2)T‎، ولنفترض أن المحاور في كلا الإطارين مُدرَّجة باستخدام الوحدات نفسها (سم مثلًا). يكون طول الشعاع باستخدام التمثيل الأول هو: ‪√( 82 + 62 ) = √( 64 + 36 )= √( 100 )= 10.0 ويكون طول الشعاع باستخدام التمثيل الثاني هو: ‪√( 9.82 + 22 ) = √( 96 + 4 ) = √( 100 ) = 10.0 ولكن هل ستنجح العملية الحسابية إذا وضعنا ذيل الشعاع في مكان آخر من الإطار؟ نعم، فليس للشعاع موضع محدّد، لذلك يمكن وضع الذيل في أيّ مكان تريده. الطول قيمة موجبة أو صفرية بما أن مربع الطول يساوي مجموع المربعات، وينتج عن تربيع الأعداد الحقيقية قيمة صفرية أو موجبة، فهذا يعني أنه يجب أن يكون الطول دائمًا صفرًا أو عددًا موجبًا. ‪| a | = | (a1, a2, a3 )T | = √( a12 + a22 + a32 ) >= 0 يكون طول الشعاع ثلاثي الأبعاد صفرًا فقط عندما يكون هذا الشعاع هو الشعاع الصفري، إذ يُمثَّل الشعاع الصفري ثلاثي الأبعاد في جميع الإطارات الإحداثية كما يلي: ‪0 = (0, 0, 0)T ويكون طول الشعاع الصفري هو: ‪| 0 | = √( 02 + 02 + 02 ) = 0 يكون طول الشعاع الصفري ثنائي الأبعاد صفرًا أيضًا، وهو الشعاع ثنائي الأبعاد الوحيد الذي يكون طوله صفرًا. إذًا هل سيكون للشعاعين المتساويين الطول نفسه، وهل سيكون الشعاعان اللذان لهما الطول نفسه متساويين دائمًا؟ سيكون للشعاعين المتساويين الطول نفسه، إذ يجب أن تكون عناصرهما المتقابلة متساويةً، لذا يجب أن تكون عمليات التربيع المتقابلة متساوية أيضًا، وبالتالي يجب أن يكون المجموع متساويًا، ويجب أن يكون الطول متساويًا. لن يكون الشعاعان اللذان لهما الطول نفسه متساويين دائمًا، إذ يمكن أن يكون مجموع مربعات العناصر متساويًا دون أن تكون العناصر نفسها متساوية. طول الشعاع السالب إذا كان v شعاعًا، فإن ‎-v هو شعاع يؤشّر إلى الاتجاه المعاكس، وإذا كان تمثيل v هو ‎(a, b, c)T‎، فسيكون تمثيل ‎-v هو ‎(-a, -b, -c)T‎، فما هي العلاقة بين طول الشعاعين v وطول ‎-v؟ العلاقة هي: ‪| v | = |-v| الأشعة ذات الاتجاهات المتعاكسة يوضّح المخطط البياني التالي بيانيًا شعاعين باتجاهين متعاكسين في فضاء ثنائي الأبعاد: يمكنك تمثيل المخطط البياني السابق رياضيًا كما يلي: ‪| v | = |(a, b, c)T| = √( a2 + b2 + c2) ‪|-v | = |(-a, -b, -c)T| = √( -a2 + -b2 + -c2) = √( a2 + b2 + c2 ) يمكن القول أن الشعاعين لهما الطول نفسه، ولكنهما يؤشّران إلى اتجاهين متعاكسين كما سنوضّح في المقال التالي. يمكن حساب طول الشعاع الذي تمثله المصفوفة العمودية ‎(1, -1, 1 )T‎ كما يلي: ‪√( 12 + -12 + 12) = √3 ترجمة -وبتصرُّف- للفصل Vector Length من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: كيفية جمع الأشعة الهندسية للتصاميم ثلاثية الأبعاد كيفية جمع وطرح المصفوفات العمودية والمصفوفات السطرية الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد

تعرّفنا في المقال السابق على جمع المصفوفات العمودية الذي يُعَد إجراءً سهلًا، وسنوضّح في هذا المقال سبب كون هذا الإجراء مفيدًا من خلال مناقشة كيفية تمثيله لعملية جمع الأشعة. سنتعرّف في هذا المقال على المواضيع التالية: جمع الأشعة. جمع الأشعة باستخدام قاعدة الرأس إلى الذيل Head to Tail. قاعدة الرأس إلى الذيل في فضاء ثلاثي الأبعاد. الخاصية التجميعية Associative لجمع الأشعة. الخاصية التبديلية Commutative لجمع الأشعة. الإطارات الإحداثية Coordinate Frames. تمثيل النقاط الهندسية باستخدام إطارات الإحداثيات والمصفوفات العمودية. تمثيل الأشعة باستخدام المصفوفات العمودية. جمع الأشعة باستخدام المصفوفات العمودية. استخدام متوازي الأضلاع في عملية جمع الأشعة. متراجحة المثلث Triangle Inequality. الأشعة المرتبطة الخطية Collinear. جمع الأشعة الصفرية. عملية جمع شعاع ونقطة. تذكير: اجمع المصفوفتين العموديتين التاليتين: a = ( 3, 2 )T b = (-2, 1 )T والجواب هو: a + b = ( 1, 3 )T الأشعة في الفضاء ثنائي الأبعاد تُعَد الأشعة كائنات هندسية يمكن تمثيلها بطرق متعددة، ولكن يجب أن نفهم الفرق بين الكائن الهندسي (مثل النقطة أو الشعاع)، وطريقة تمثيله (باستخدام مصفوفة عمودية غالبًا). يوضّح المخطط البياني السابق النقاط A و B و C في فضاء ثنائي الأبعاد؛ حيث يُعبَّر عن الإزاحة Displacement بمسافة واتجاه، فالشعاع u هو الإزاحة من النقطة A إلى النقطة B، أما الشعاع v فهو الإزاحة من النقطة B إلى النقطة C. بينما يعبٌر الشعاع w عن الإزاحة من النقطة A إلى النقطة C؛ ويكون تأثير التحرك عبر الإزاحة u ثم عبر الإزاحة v هو تأثير التحرك عبر الإزاحة w نفسه وبالتالي يمكن القول أن: u + v = w عدم اعتمادية عملية جمع الأشعة على موضعها هل تعتمد عملية جمع الأشعة على مكان وجودها؟ لا، فليس للأشعة موضع محدّد. توضّح النقاط في المخطط البياني السابق كيفية حساب التأثير المشترك لإزاحتين من خلال جمعهما، ولكن لم يتضمّن جمعُ الإزاحات النقاط فعليًا، حيث يظهر جمع الأشعة عادةً كما في المخطط البياني السابق، الذي يوضح أن تأثير التحرك عبر الإزاحة u ثم التحرك عبر الإزاحة v هو تأثير التحرك عبر الإزاحة w نفسه. لنفترض مثلًا أنك ترغب في نقل جميع نقاط كائن هندسي عبر الإزاحة u، ثم عبر الإزاحة v. يمكنك تطبيق ذلك من خلال تحريك كل نقطة عبر الإزاحة w. قاعدة الرأس إلى الذيل Head-to-Tail جرب رسم الخط الذي يمثل مجموع الشعاعين s و t: والحل باستخدام قاعدة الرأس إلى الذيل هو: يمكن جمع الشعاعين v و u في المخطط البياني التالي من خلال تحريك الشعاع v مع الحفاظ على طوله ومنحاه Orientation حتى يلمس ذيلُ هذا الشعاع رأسَ الشعاع u، والناتج هو الشعاع المتشكّل من ذيل الشعاع u إلى رأس الشعاع v: اجمع الشعاعين e و d: والحل هو: يوضّح المخطط البياني السابق تحريك الشعاع e للأعلى حتى يلامس ذيله رأس الشعاع d، والناتج هو الشعاع المتشكّل من ذيل الشعاع d إلى رأس الشعاع e . جمع الأشعة في الفضاء ثلاثي الأبعاد يوضّح المخطط البياني التالي جمع الشعاعين a و b ثلاثيّي الأبعاد لتشكيل الشعاع c. وضعنا الصندوق ثلاثي الأبعاد للمساعدة على تصوّر الأبعاد الثلاثية، إذ تعمل قاعدة الرأس إلى الذيل في الفضاء ثلاثي الأبعاد أيضًا. تحدّد قاعدة الرأس إلى الذيل مثلثًا مُوجَّهًا في الفضاء ثلاثي الأبعاد عند جمع شعاعين في فضاء ثلاثي الأبعاد. الخاصية التجميعية Associative لجمع الأشعة هل يمكن جمع ثلاثة أشعة مثل الأشعة a و b و d في المخطط البياني التالي؟ نعم يمكن ذلك، والنتيجة هي الإزاحة الإجمالية الناتجة عن اتباع كل شعاع بدوره. يوضّح المخطط البياني التالي نتيجة جمع ‎(a + b) + d = c + d‎، والنتيجة هي شعاع بطول واتجاه مماثل لقطر الشكل. يوضّح المخطط البياني التالي نتيجة جمع ‎a + (b + d)‎، والنتيجة هي نفسها، ويُعَد ذلك دليلًا على الخاصية التجميعية لجمع الأشعة: a + (b + c) = (a + b) + c يمكن تطبيق هذه القاعدة في جميع الأبعاد، إذ تكون الأشعة الهندسية للرسوميات الحاسوبية غالبًا ثنائية وثلاثية الأبعاد بالرغم من إمكانية وجود أبعاد أعلى بصورة عامة. تعني الخاصية التجميعية أنه يمكن كتابة مجموع عدة أشعة مثل: a + b + c + d + e بدون قوسين. الخاصية التبديلية Commutative لجمع الأشعة لنفترض أنك تمشي مسافة خمس بنايات شمالًا، ثم ثلاث بنايات شرقًا، ولكن إذا مشيت ثلاث بنايات شرقًا ثم خمس بنايات شمالًا، فهل ستصل إلى المكان نفسه؟ نعم، هذا صحيح. يُعَد جمع الأشعة عملية تبديلية مثل جمع الأعداد الحقيقية تمامًا: a + b = b + a إذا بدأت من النقطة P، فسينتهي بك الأمر في المكان نفسه بغض النظر عن الإزاحة (a أو b) التي ستأخذها أولًا. سينتج الشعاع c عن كلٍّ من عمليتي الجمع a + b و b + a عند تطبيق قاعدة الرأس إلى الذيل، ولكن هل يمكن تطبيق الخاصية التبديلية على جميع الأبعاد؟ نعم، يمكن ذلك. تمثيل النقاط باستخدام المصفوفات العمودية يمكن تمثيل النقاط باستخدام المصفوفات العمودية، ولكن يجب أولًا اتخاذ قرار بشأن الإطار الإحداثي Coordinate Frame الذي يُسمَّى أحيانًا بالإطار فقط. ويتكون الإطار الإحداثي من نقطة مميزة P0‎ تسمى نقطة الأصل Origin، ومن محور لكل بُعد يُسمَّى X و Y غالبًا، فهناك محوران في الفضاء ثنائي الأبعاد، وثلاثة محاور تُسمَّى X و Y و Z في الفضاء ثلاثي الأبعاد. لنبدأ بالفضاء ثنائي الأبعاد، حيث يُظهِر المخطط البياني الأيسر عالمًا افتراضيًا بسيطًا إلى حدٍ ما في فضاء ثنائي الأبعاد، إذ تكون النقاط والأشعة موجودةً في الفضاء بصورة مستقلة عن أيّ إطار إحداثي، بينما يوضّح المخطط البياني الأوسط العالم الافتراضي نفسه مع إطار إحداثي يتكون من نقطة معينة P0‎ ومحورين، وتُمثَّل النقطة A في هذا الإطار الإحداثي بالمصفوفة العمودية ‎(2, 2)T‎. يُظهر المخطط البياني الأيمن العالم الافتراضي نفسه مع إطار إحداثي مختلف، إذ تُمثَّل النقطة A في هذا الإطار الإحداثي بالمصفوفة العمودية ‎(2, 3)T‎. إذًا، كيف تُمثَّل النقطة B باستخدام الإطار الإحداثي الأول، وباستخدام الإطار الإحداثي الثاني؟ تُمثَّل النقطة B باستخدام الإطار الإحداثي الأول بالمصفوفة العمودية ‎(6, 2)T‎، وتُمثَّل باستخدام الإطار الإحداثي الثاني بالمصفوفة العمودية ‎(4.8, 1.6)T‎. تمثيل النقاط باستخدام إطارات إحداثية مختلفة الفكرة الأساسية -والمربكة في كثير من الأحيان- هي أنه يوجد في برنامج الرسوميات عالم افتراضي واحد، ولكن قد يكون هناك أيّ عددٍ من الإطارات الإحداثية قيد الاستخدام، إذ لكل كائنٍ إطاره الخاص غالبًا، بحيث يُستخدَم إطار مختلف لوصف مواقع الكائنات؛ ويمكن استخدام إطارٍ آخر لمجال الرؤية، ويُعَد ذلك شيئًا تفعله فعليًا طوال الوقت مع العالم الحقيقي، ولكنه يكون الجزء الصعب في معرفة كيفية العمل مع العالم الافتراضي. لنفترض أن لديك مزهريةً موضوعةً على طاولة مثلًا، وأنت تتحدث مع صديق عبر الهاتف وترغب في وصف المزهرية له ومكانها وكيف تبدو لك. يمكنك وصف المزهرية بأنها كرة مركزها نقطة الأصل ومتقاطعة مع أسطوانة محورها هو المحور y، ويُعَد ذلك وصفًا للمزهرية في إطارها الخاص. يمكنك وصف موقع المزهرية بأنه "يبعد 20 سم تقريبًا من الحافة الأمامية للطاولة و30 سم من الحافة اليمنى"، واستخدمنا بذلك إطارًا آخر لوصف الموقع. يمكنك أيضًا التحدث عن كيفية مشاهدتك للطاولة من مسافة 2 متر تقريبًا وارتفاع 1.5 متر، ويستخدم ذلك إطارًا آخر لوصف مجال رؤيتك. يمكن أن تتجول أيضًا حول الطاولة معجبًا بالمزهرية الجميلة، وعندها يجب أن تستخدم إطارًا آخر لوصف مجال رؤيتك الجديد. لنفترض أنك خرجت للمشي، واقترب منك شخص غريب وسألك عن الاتجاهات إلى مكتب البريد، فما هو إطار الإحداثيات الذي ستستخدمه؟ هل ستستخدم خط العرض وخط الطول استنادًا إلى جرينتش في إنجلترا؟ أم ستستخدم عدد مباني المدينة على يسار ويمين موقعك الحالي؟ حسنًا، إن لم يكن لدى هذا الشخص الغريب جهاز استقبال GPS، فيُرجَّح أن يكون إطار إحداثيات مباني المدينة هو الأكثر فائدة. تمثيل الأشعة باستخدام المصفوفات العمودية لنعُد إلى عالمنا الافتراضي، حيث تكون الإزاحة من النقطة A إلى النقطة B هي الشعاع v، ولكن لا يعتمد الشعاع على أيّ نظام إحداثي. يمكن تمثيل الإزاحة باستخدام نظام الإحداثيات الأول (المخطط البياني الأوسط) بأنها: (الفرق في إحداثيات y, الفرق في إحداثيات x) وبالتالي تكون الإزاحة هي: ‎(4, 0)T‎ في هذا المخطط البياني، أي التحرّك بمقدار 4 وحدات من النقطة A باتجاه المحور x للوصول إلى النقطة B، بينما يُمثَّل الشعاع نفسه بالمصفوفة العمودية ‎(2.8, -1.4)T‎ في نظام الإحداثيات الثاني (الرسم البياني الأيمن). تُمثَّل كلٌّ من النقاط والأشعة باستخدام المصفوفات العمودية، فهل يُحتمَل أن يكون ذلك مربكًا؟ نعم هذا محتمل، إذ يؤدي هذا الارتباك إلى استخدام الإحداثيات المتجانسة Homogeneous Coordinates، والتي هي طريقة أخرى لتمثيل النقاط والأشعة باستخدام المصفوفات العمودية، ولكننا لن نشرحها في في هذا المقال. تمثيل جمع الأشعة باستخدام جمع المصفوفات العمودية إذا كانت الأشعة مُمثلَّة بالمصفوفات العمودية، فسنمثّل جمع الأشعة بجمع المصفوفات العمودية كما يلي: a = ( 3, 2 )T b = ( -2, 1 )T a + b = c = ( 1, 3 )T يوضح المخطط البياني السابق قاعدة الرأس إلى الذيل المُستخدَمة لجمع الشعاعين a و b للحصول على الشعاع c، وينتج عن جمع المصفوفتين العموديتين a و b المصفوفة العمودية c التي هي التمثيل الصحيح للشعاع c. تغيير ترتيب معاملات عملية الجمع مع الإجابة نفسها جرب حساب c = b + a للمصفوفتين العموديتين a و b السابقتين نفسهما، وستكون الإجابة نفسها هي: b + a = c = ( 1, 3 )T اتبع الخطوات التالية التي يكون فيها الشعاع b بمثابة شعاع البداية لإنشاء الرسم البياني التالي: ارسم الشعاع الأول b على شكل سهم، بحيث يكون ذيله عند نقطة الأصل. ارسم الشعاع الثاني a على شكل سهم، بحيث يكون ذيله عند نقطة رأس الشعاع الأول. يكون مجموعهما هو السهم المتشكّل من نقطة الأصل إلى رأس الشعاع الثاني. ملاحظة: تذكّر أن الأشعة ليس لها موقع محدّد، لذا يمكنك رسم مثيل للشعاع بحيث يبدأ ذيله من أيّ نقطة تريدها. يجب أن تكون نتيجة الجمع هي نفسها بما أن جمع الأشعة عملية تبديلية. تذكير: تُعَد عملية جمع الأشعة وجمع المصفوفات العمودية عملية تجميعية أيضًا. تدريب عملي ليكن لدينا الشعاعان: R = ( 4, 3 )T S = ( 1, 2 )T أوجد ناتج عملية الجمع: T = R + S يمكنك إيجاد الناتج من خلال استخدام جمع المصفوفات العمودية وقاعدة الرأس إلى الذيل، وسيكون الناتج عند تطبيق القاعدة هو: T = (5, 5)T ولنجمع الآن الشعاعين بترتيب معاكس كما يلي: T = S + R حيث يكون الشعاعان هما: S = ( 1, 2 )T R = ( 4, 3 )T وتبقى الإجابة نفسها: T = (5, 5)T استخدام متوازي الأضلاع في عملية جمع الأشعة هناك طريقتان لتشكيل عملية الجمع: T = S + R T = R + S حيث يكون الشعاعان هما: R = ( 4, 3 )T S = ( 1, 2 )T هناك طريقتان للرسم اعتمادًا على ذيل السهم الذي تضعه عند نقطة الأصل، بحيث إذا استخدمتَ كلا الطريقتين، فستحصل على متوازي أضلاع مع ناتج جمع الأشعة الذي يُمثَّل بسهم قطري يبدأ ذيله من نقطة الأصل. قد تتساءل عن ما هو متوازي الأضلاع Parallelogram وعمّا إذا كانت مادة الهندسة التي تعلّمتها في المدرسة الثانوية غامضة قليلًا، فمتوازي الأضلاع هو شكل رباعي فيه كل ضلعين متقابلين متوازيين ومتساويين في الطول، مثل السهمين الأزرقين الممثلين للشعاع s اللذين لهما الطول والاتجاه نفسه، والسهمين الأخضرين الممثلين للشعاع r اللذين لهما الطول والاتجاه نفسه. رحلة ثنائية الاتجاه أوجد ناتج ما يلي: w = u + v إذا كان: u = ( -3, 2 )T v = ( 1, -5 )T والجواب هو: w = ( -2, -3 )T يوضح المخطط البياني السابق عملية الجمع w= u + v. لنفترض أن نملةً ما تبدأ التحرك من نقطة الأصل وتسير على طول الشعاع u، ثم تسير على طول الشعاع v حتى تصل إلى رأس الشعاع w، وتبدأ النملة الثانية من نقطة الأصل وتسير على طول الشعاع w حتى تصل إلى نهايته، وبالتالي ستصل كلتا النملتين إلى النقطة نفسها. جمع الإزاحات وجمع الأطوال غير متساويين هل مشت النملتان المسافة نفسها في المثال السابق؟ في هذه الحالة، لا! فمن الواضح أن المشي في خط مستقيم إلى الوِجهة النهائية أقصر. لا يُعَد جمع الإزاحات (أو الأشعة) مثل جمع أطوالها، إذ ينتج عن جمع الشعاعين u و v شعاع أقصر من طول الشعاع u مع طول الشعاع v في المثال السابق؛ ويمكنك ملاحظة ذلك حاليًا من خلال النظر إلى المخطط البياني السابق، وتذكّر أن "الخط المستقيم هو المسافة الأقصر بين نقطتين" (سنناقش ذلك لاحقًا باستخدام صيغة فيثاغورس). تسمى هذه الحقيقة الرياضية بمتراجحة المثلث Triangle Inequality، وهي تنص على أن ناتج جمع أي طولين من أضلاع المثلث أكبر من طول الضلع الثالث. طول (v + u) <= طول (u) + طول (v) إليك حالة يكون فيها طول ناتج الجمع أقصر بكثير من مجموع الأطوال: e = ( 5, 4 )T g = ( -4.9, -3.9 )T e + g = (0 .1, 0.1 )T ملاحظة: نقلنا الشعاع g قليلًا من المكان الذي ينبغي أن يكون فيه للتوضيح. الأشعة ذات الاتجاه نفسه هل يمكنك التفكير في حالة يكون فيها طول ناتج الجمع مساويًا لمجموع طولي شعاعي الدخل؟ نعم يمكن ذلك إذا كان لأحد الشعاعين اتجاه الشعاع الآخر. يمكن توضيح هذه الحالة في المخطط البياني التالي، إذ تُستخدَم قاعدة الرأس إلى الذيل لجمع شعاعين يؤشّران إلى الاتجاه نفسه، وتُسمَّى الأشعة ذات الاتجاه نفسه بأنها مرتبطة خطية Collinear. نقلنا شعاع ناتج الجمع قليلًا عن مكانه الصحيح حتى تتمكّن من رؤيته. بعد ذلك جمعنا الشعاعين ‎(4, 3)T‎ و ‎(2, 1.5)T‎، والناتج هو ‎(6, 4.5)T‎. يمكنك حاليًا تحديد ما إذا كان هناك شعاعان لهما الاتجاه نفسه من خلال النظر إلى الصورة أو باستخدام المفاهيم الهندسية، وستتعرّف لاحقًا على إجراءٍ لاختبار ما إذا كان هناك شعاعان يؤشّران إلى الاتجاه نفسه. يعبِّر هذا المثال عن حالةٍ تطبِّق إشارة المساواة "=" الموجودة في الصيغة التالية: طول (v + u) <= طول (u) + طول (v) جمع الأشعة الصفرية هل يمكنك التفكير في حالةٍ أخرى تطبّق إشارة المساواة "=" الموجودة في الصيغة السابقة؟ نعم، عندما يكون أحد الشعاعين شعاعًا صفريًا كما يلي: طول ‎(0 + u)‎ <= طول (u) + طول (0) اجمع المصفوفة الصفرية ‎( 0, 0 )T‎ مع المصفوفة ‎( 4, 3 )T‎، فإذا مثّلت المضفوفة ‎( 0, 0 )T‎ شعاع إزاحة، فهذا يعني عدم تطبيق أيّ شيء لتغيير موضع الشعاع الآخر. جمع النقاط والأشعة لنفترض أنك تريد جمع الشعاع ‎(1, 2)T‎ والنقطة ‎(4, 4)T‎. إذا كان ذلك منطقيًا، فأجرِ هذه العملية، وما هو نوع الكائن الناتج؟ يكون الناتج نقطة كما يلي: ‭‭(4, 4)T + (1, 2)T = ( 5, 6 )T إذا كان الشعاع ‎(1, 2)T‎ إزاحة (أي مقدار يمكن تغيير قيمة x به، ومقدار يمكن تغيير قيمة y به)، فيجب أن تكون النتيجة نقطة في موقع جديد كما يلي: ‭(4, 4)T + (1, 2)T = ( 5, 6 )T هذه إحدى الحالات التي يكون فيها استخدام التمثيل (أي المصفوفات العمودية) نفسه لكل من النقاط والأشعة أمرًا مربكًا، لذا يجب عليك تتبّع نوع الكائن الذي تمثله كل مصفوفة. تنتج نقطةٌ عن جمع شعاع إزاحة ونقطة كما في المخطط البياني التالي: يُعَد جمع كائنين رياضيين من نوعين مختلفين غريبًا قليلًا، ولا تنسَ أن إشارة الجمع "+" إشارة قابلة للتحميل الزائد overloaded. الانسحاب Translation تُسمَّى عملية جمع شعاع ونقطة بالانسحاب Translation، ويُقال أحيانًا أن النقطة الأصلية مسحوبةً إلى موقع جديد. قد تكون المصطلحات هنا مربكةً قليلًا، إذ ينتج عن جمع شعاع ونقطة من الناحية الرياضية نقطةٌ جديدة، بحيث تبقى النقطة الأولى دون تغيير، ولكن من الجيد التفكير في الصور "التي تتحرك عبر الشاشة" عند جمع أشعة الإزاحة والنقاط الخاصة بها في مصطلحات الرسوميات الحاسوبية، لذا قد تسمع أحيانًا مصطلحات مثل "تحريك نقطة" و"النقطة القديمة" و"النقطة الجديدة". لقد رأينا تطبيق العمليات التالية: شعاع + شعاع. نقطة + شعاع. نقطة - نقطة. فهل تفترض أنه يمكن إجراء العملية نقطة + نقطة؟ لا يُعَد جمع نقطتين شيئًا هندسيًا. يمكنك تشكيل مجموع شعاعين عموديين يمثلان نقاطًا ميكانيكيًا، ولكن النتيجة لا تكون ذات معنى فعلي. لقد وصلنا إلى نهاية هذا المقال، وسنناقش في المقال التالي العمليات على الأشعة بصورة أكبر، وسنناقش لاحقًا مزيدًا من العمليات على الأشعة. ترجمة -وبتصرُّف- للفصل Vector Addition من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا المقال السابق: كيفية جمع وطرح المصفوفات العمودية والمصفوفات السطرية الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد

سنناقش في هذا المقال كيفية جمع وطرح المصفوفات العمودية والسطرية ولكن لنتعرّف على بعض المصطلحات التي سنستخدمها: النقطة Point: كائن هندسي، وهو موقع في فضاء ثلاثي الأبعاد أو ثنائي الأبعاد. الشعاع Vector: كائن هندسي له خصائص الاتجاه والطول، ولكن ليس لديه خاصية الموقع. المصفوفة العمودية Column Matrix: قائمة مرتبة من الأعداد تُرتَّب ضمن عمود. المصفوفة السطرية Row Matrix: قائمة مرتبة من الأعداد تُرتَّب ضمن صف. العنصر Element: أحد الأعداد التي تشكل المصفوفة العمودية أو السطرية. البعد Dimension: عدد العناصر في مصفوفة عمودية أو سطرية. الإزاحة Displacement: هو الفرق بين موقعين، ويعبَّر عنه باستخدام شعاع. كما سنوضّح في هذا المقال المواضيع التالية: منقول Transpose المصفوفة العمودية أو السطرية. جمع المصفوفات العمودية والمصفوفات السطرية. الخاصية التبديلية لجمع المصفوفات. الخاصية التجميعية لجمع المصفوفات. طرح المصفوفات العمودية والمصفوفات السطرية. الخاصية غير التبديلية لطرح المصفوفات. منقول مصفوفة Transposition ماذا تُسمَّى عملية قَلب مصفوفة العمودية، أو ماذا تُسمَّى عملية قَلب مصفوفة سطرية إلى مصفوفة عمودية؟ تسمّى عملية المنقول Transposition. تُعَد المصفوفة السطرية والمصفوفة العمودية من نوعين مختلفين حتى لو كان لهما البعد نفسه وتحتويان على العناصر نفسها، لذا يُستخدَم الحرف العُلوي "T" عند كتابة مصفوفة عمودية مثل صفٍ من الأعداد، إذ يكون العنصر الأول في المصفوفة العمودية هو العنصر الموجود أعلى العمود، ويكون العنصر الأول في المصفوفة السطرية هو العنصر الموجود على يسار الصف. سنوضح فيما يلي طريقتين لكتابة المصفوفة العمودية نفسها، إذ تُكتَب عناصر المصفوفة العمودية بالطريقة نفسها بغض النظر عن كيفية عرض المصفوفة العمودية. يعني وجودُ حرف T العُلوي في المصفوفة العمودية قلبَ العمود إلى صف، وينتج عنه مصفوفة سطرية، وتستخدم بعض الكتب حرف t صغير. ما هو : ‎(1, 2, 3)T T‎؟ ‭( 1, 2, 3 )T T = ( 1, 2, 3 ) يؤدي تطبيق المنقول مرتين إلى العودة إلى ما بدأت به. يبدو هذا واضحًا الآن، ولكن قد يكون من المفيد تذكّر ذلك لاحقًا عند تطبيق المعالجة الجبرية. جمع المصفوفات العمودية يمكن جمع مصفوفتين عموديتين لهما البُعد نفسه، وتنتج مصفوفة عمودية لها البعد نفسه أيضًا، وينطبق الشيء نفسه على المصفوفات السطرية. تُطبَّق عملية الجمع من خلال جمع العناصر المتقابلة لمصفوفات الدخل لإنتاج العناصر المقابلة لمصفوفة الخرج كما يلي: ‭( 42, -12 )T + ( 8, 24 )T = ( 50, 12 )T ‭( 32.98, -24.71, 9.392 )T + ( -32.98, +24.71, -9.392 )T = (0, 0, 0)T ‭( 9.2, -8.6, 3.21, 48.7 ) + ( -2.1, 4.3, 1.0, 2.3 ) = ( 7.1, -4.3, 4.21, 51.0 ) ‭( 1, 2, 3 ) + ( 10, 20, 30 ) = ( 11, 22, 33 ) إذا كان a و b مصفوفتين من النوع نفسه، فإن ‎a + b = c‎ يعني أن كل عنصر ci = ai + bi‎ أوجد ناتج ما يلي: ‎( 2, -2 )T + ( 8, 6 )T‎ الجواب: ‭( 2, -2 )T + ( 8, 6 )T = ( 10, 4 )T جمع المصفوفات ثلاثية الأبعاد يجب أن تكون المصفوفات التي تجمعها لها البُعد والنوع نفسه سواءً كانت عمودية أم سطرية. يجري التعامل مع كل بُعد بصورة مستقلة عن الأبعاد الأخرى عند جمع المصفوفات، فمثلًا سيكون لديك ثلاث عمليات جمع منفصلة باستخدام العمليات الحسابية العادية عند جمع مصفوفتين عموديتين ثلاثيتي الأبعاد، إذ تُجمَع العناصر الأولى من المصفوفات التي تمثل معاملات عملية الجمع لتكوين العنصر الأول من المصفوفة الناتجة. أوجد ناتج ما يلي:‭ ( 8, 4, 6 )T + ( 2, -2, 9 )T ‭ ( 2, -2, 9 )T + ( 8, 4, 6 )T الجواب: ‭( 8, 4, 6 )T + ( 2, -2, 9 )T = ( 10, 2, 15 )T ‭( 2, -2, 9 )T + ( 8, 4, 6 )T = ( 10, 2, 15 )T الخاصية التبديلية Commutative لجمع المصفوفات تُعَد عملية جمع المصفوفات عملية تبديلية، أي أن: a + b = b + a، وينطبق ذلك على المصفوفات السطرية والعمودية بجميع أبعادها، إذ يمكن القول أن: a + b + c = b + c + a = c + a + b = …..‎. تعني الخاصية التبديلية أن ترتيب جمع المصفوفات غير مهم، إذ تعمل المصفوفات باستخدام طريقة عمل الأعداد نفسها بالنسبة للجمع: 1 + 2 = 2 + 1، فالمصفوفات والأعداد عادةً لا تعمل بالطريقة نفسها ولكنها كذلك بالنسبة لعملية الجمع. أوجد ناتج ما يلي: ‎( -1, -2, 3 )T + ( 1, 2, -3 )T‎ الجواب: ‭( -1, -2, 3 )T + ( 1, 2, -3 )T = ( 0, 0, 0 )T المصفوفة العمودية الصفرية ليكن لدينا مثلًا مصفوفة صفرية كما يلي: ‭( 73.6, -41.4 )T + ( 0.0, 0.0 )T = (73.6, -41.4 )T تُسمَّى المصفوفة التي تكون جميع عناصرها أصفارًا بالمصفوفة الصفرية Zero Matrix، ويكون ناتج جمع المصفوفة الصفرية والمصفوفة a لهما النوع نفسه هو المصفوفة a. نرمّز المصفوفة الصفرية بالرمز 0 (صفر بالخط العريض) الذي يختلف عن 0 (العدد الحقيقي صفر)، ويحدّد السياق الذي ترى فيه الرمز 0 ما إذا كانت مصفوفة صفرية سطرية أم عمودية وعدد العناصر التي تحتوي عليها. فإذا رأيت ‎(73.6, -41.4 )T + 0‎ ، فيمكنك أن تفترض ما هو النوع الصحيح للمصفوفة 0 والمناسب للتعبير. الخاصية التجميعية Associative لجمع المصفوفات أوجد ناتج ما يلي: ‎( 2, 5, -9 ) + ( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 )‎ الجواب: ( 2, 5, -9 ) + ( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 ) = ( -32.034, 94.79, 201.062 ) + ( -2, -5, 9 ) + ( 2, 5, -9 ) = ---------------------------- ( -32.034, 94.79, 201.062 ) + ( 0, 0, 0) = ( -32.034, 94.79, 201.062 ) قد يفقد بعض الطلاب صبرهم عندما يجمّعون المصفوفتين الأوليتين، ثم يجمّعون الناتج مع المصفوفة الثالثة، ولكن يدرك بعضهم أنه يمكن إعادة ترتيب المصفوفات إلى ترتيب أكثر ملاءمة بما أن جمع المصفوفات يُعَد عملية تبديلية، إذ يمكنهم اختيار عملية الجمع "+" التي يريدون تطبيقها أولًا بعد أن تصبح المصفوفات في ترتيب مناسب. يُعَدّ جمع المصفوفات عملية تجميعية، وهذا يعني أن: ‭( a + b ) + c = a + ( b + c ) أي يمكن جمع المصفوفتين a و b‎ ثم جمع النتيجة مع المصفوفة c، وستكون النتيجة النهائية هي نفسها كما لو جمعت المصفوفة a إلى نتيجة جمع المصفوفتين b و c. يمكن تطبيق ذلك على المصفوفات السطرية والعمودية بجميع أبعادها. هل يمكنك إيجاد ناتج ما يلي في الوقت المناسب؟ ‎( 25.1, -19.6 ) + ( -5.0, 9.0 ) + ( 12.4, 8.92 ) + ( -20.1, 10.6 )‎ الجواب: ( 25.1, -19.6 ) + ( -5.0, 9.0 ) + ( 12.4, 8.92 ) + ( -20.1, 10.6 ) = ------------- --------------- \ / \ / \ / \ / ( 25.1, -19.6 ) + ( 12.4, 8.92 ) + ( -25.1, 19.6 ) --------------- --------------- \ / \ / \ / \ / \ / ( 0.0, 0.0 ) + ( 12.4, 8.92 ) = ( 12.4, 8.92 ) بعض الأشياء التي لا يمكن استخدامها عند جمع المصفوفات يعني الرمز "+" زيادة التحميل Overloaded في مصطلحات علوم الحاسوب، مما يعني أن العملية المُستدعاة تعتمد على نوع المعاملات، فمثلًا: يعني الرمز + هنا جمع أعداد حقيقية: 1.34‎ + -9.06 يعني الرمز + هنا جمع مصفوفات عمودية: ‎( 84.02, 90.31 )‎T + ( -14.23, 10.85 )T‎ بينما لا تعطي الأمور التالية أيّ معنًى: لا يمكن جمع عدد ومصفوفة: 34.5‎ + ( 84.02, 90.31 )T‎ لا يمكن جمع مصفوفة سطرية ومصفوفة عمودية: ‎( 84.02, 90.31 )‎ + ( -14.23, 10.85 )T‎ ‎* لا يمكن جمع مصفوفات ذات أبعاد مختلفة: ‎( 84.02, 90.31 ) + ( -14.23, 10.85, 32.75 )‎ تكون هذه المشاكل واضحة عند كتابة العناصر كما سبق، ولكنها تكون أقل وضوحًا عند استخدام الرموز المتغيرة كما يلي: لا يمكن جمع عدد ومصفوفة a + x‎. يجب التأكد من أن المعاملين x + y من النوع نفسه. يمكن إجراء عملية الجمع: ‎( 4.5, x1, w ) + ( -2.3, 3, y2 )‎ كما يلي: ‭( 4.5, x1, w ) + ( -2.3, 3, y2 ) = ( 2.2, x1 +3, w+ y2 ) طرح المصفوفات يمكن طرح مصفوفتين من النوع نفسه وتنتج مصفوفة ثالثة من ذات النوع، إذ يمكن طرح مصفوفتين من خلال طرح العناصر المتقابلة، مع الحرص على إبقاء العناصر بالترتيب نفسه كما يلي: ‭(10, 8, 12 ) - (2, 14, 9 ) = ( 10 - 2, 8 - 14, 12 - 9 ) = ( 8, -6, 3 ) إذا كانت a و b مصفوفتان من النوع نفسه، فإن ‎a - b = c‎ تعني أن كل عنصر ci = ai - bi‎ ليست عملية الطرح تبديلية أوجد ناتج ما يلي: ‭(22, 5, -12 ) - (10, -5, 3 ) ‭(10, -5, 3 ) - (22, 5, -12 ) الجواب: ‭(22, 5, -12 ) - (10, -5, 3 ) = ( 22 - 10, 5 - (-5), -12 - 3 ) = ( 12, 10, -15 ) ‭(10, -5, 3 ) - (22, 5, -12 ) = ( 10 - 22, (-5) - 5, 3 - (-12) ) = (-12, -10, 15 ) حقيقة رياضية: لا تُعَد عملية الطرح تبديلية، وهذا يعني أنه لا يمكنك تغيير الترتيب عند طرح المصفوفتين a - b. يمكن إيجاد معاكس مصفوفة ‎-a‎ من خلال إيجاد معاكس كل عنصر من عناصر هذه المصفوفة كما يلي: ‭-(22, 5, -12 ) = ( -22, -5, 12 ) ‭-( 19.2, 28.6, 0.0 )T = ( -19.2, -28.6, 0.0 )T يمكن القول أنه إذا كانت a هي ( a0, a1, …, a2‎) فإن ‎-a تعني ‎(-a0, -a1, …, -a2)‎. إدخال الإشارة السالبة داخل الأقواس أوجد ناتج عملية الطرح التالية: ‎( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T‎ الجواب: ‭( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T = ‭( -7.2 -(-2.2), -98.6 -(-2.4), 0.0 - 3.0)T = ‭( -5.0, -96.2, - 3.0)T ولكن قد تجد أن الطريقة التالية أسهل للحل: ‭( -7.2, -98.6, 0.0 )T - ( -2.2, -2.4, 3.0 )T = ‭( -7.2, -98.6, 0.0 )T + ( +2.2, +2.4, -3.0 )T = ‭( -5.0, -96.2, - 3.0)T اُستخدِمت الإشارة السالبة الخارجية لعكس إشارة المصفوفة الثانية، ثم تُجمَع المصفوفتان الناتجتان كما يلي: a - b = a + (-b) قد يكون من المفيد تذكّر ذلك، حيث يمكنك عكس إشارة المصفوفات بحيث تكون العملية هي جمع المصفوفات ثم إعادة ترتيب عملية الجمع لأن عملية الجمع تُعَد عملية تبديلية: a - b + c - d = a + (-b) + c + (-d) = (-d) + a + c + (-b) = الجمع بأيّ ترتيب تريده إليك بعض الحقائق الأخرى: ‭a + (-a) = 0 ‭a - a = 0 لاحظ أن 0 هي المصفوفة الصفرية، ولها نوع المصفوفة a نفسه ولكن تكون جميع عناصرها صفر. أجرِ العملية التالية: ‭‎( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) - ( 4, -5, -4.8 )‎ حاول إعادة الترتيب بدلًا من التسرع والحساب مباشرةً: ( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) - ( 4, -5, -4.8 ) = ( 4, -5, 6.2 ) + ( -43.132, 13.6, 86.5 ) + ( -4, 5, 4.8 ) = ( 4, -5, 6.2 ) + ( -4, 5, 4.8 ) + ( -43.132, 13.6, 86.5 ) = ( 0, 0, 11 ) + ( -43.132, 13.6, 86.5 ) = (-43.132, 13.6, 97.5 ) وقد تتخطى بعض الخطوات إذا حاولت الحساب ذهنيًا. تدريب عملي أولًا، ما هو مجموع الإزاحات الثلاثة التالية: ‭d = ( -12.4, 14.8, 0.0 )T ‭e = ( 6.2, -10.2, 17.0 )T ‭f= ( 6.2, -4.6, -17.0 )T والناتج هو: ‎(0.0, 0.0 0.0)‎T‎. ثانيًا، أوجد قيمة x و y و z بحيث يكون ما يلي صحيحًا: ‭a = ( 8.6, 7.4, 3.9 ) ‭b = ( 4.2, 2.2, -3.0 ) ‭c = ( x, y, z ) ‭a + b + c = 0 وبالتالي يمكن كتابة ما يلي: ‭a + b + c = ( 12.8, 9.6, 0.9 ) + (x, y, z) = ( 12.8+x, 9.6+y, 0.9+z ) = (0, 0, 0) لذا يجب أن يكون: ‭12.8 + x = 0; x = -12.8 ‭ 9.6 + y = 0; y = -9.6 ‭ 0.9 + z = 0; z = -0.9 استخدام الجبر في جمع وطرح المصفوفات كان التمرين السابق هو العثور على عناصر المصفوفة c عندما: a** + b + c = 0‎**، ولكن إن لم تكن على علمٍ أنها مصفوفات، فقد تميل إلى حل هذا التمرين باستخدام جبر الأعداد الحقيقية real كما يلي: ‭a + b + c = 0 ‭a + b = -c + 0 ‭(a + b) = -c ‭-(a + b) = c يمكن استخدام هذه الطريقة طالما أن المصفوفات من النوع نفسه، والعمليات هي جمع "+" أو طرح "-" فقط، وبالتالي يمكنك التظاهر بأنك تطبّق عمليات جبرية عادية. لاحظ أن المعادلة الأخيرة تعني "اجمع a مع b، ثم اعكس إشارة النتيجة لتحصل على c". لنتعمق أكثر ولننظر فقط إلى العناصر الأولى من المصفوفات: ‭( a0, … ) + ( b0, … ) + ( c0, … ) = ( 0, …) ‭( a0, … ) + ( b0, … ) = -( c0, … ) + ( 0, …) ‭( a0, … ) + ( b0, … ) = -(c0, … ) ‭( a0 + b0, … ) = -( c0, … ) ‭-( a0 + b0, … ) = ( c0, … ) ‭-( a0 + b0) = c0 إذا كان ذلك غير منظم بالنسبة لك، فامسح ذهنيًا بعض الأشياء غير المرغوب فيها كما يلي: a0 + b0 + c0 = 0 ‭a0 + b0 = -c0 + 0 ‭a0 + b0 = -c0 a0 + b0 = -c0 ‭-( a0 + b0) = c0 وتتبع العناصر الأخرى النمط نفسه، وبالتالي تكون النتيجة صحيحة بالنسبة للمصفوفة ككل. أوجد قيمة c1‎ و c0‎ بحيث يكون ما يلي صحيحًا: ‭a = ( -4, 2 )T ‭b = ( 8, 3 )T ‭c = ( c0, c1 )T ‭a + b + c = 0 ويكون الحل باستخدام الطريقة التالية: ‭a + b + c = 0 ‭a + b = -c ‭( 4, 5 )T = -( c0, c1 )T ‭-( 4, 5 )T = ( c0, c1 )T ‭(-4, -5 )T = ( c0, c1 )T وبالتالي: ‭c0 = -4 ‭c1 = -5 وصلنا إلى نهاية المقال الذي تعلّمنا من خلاله كيفية جمع وطرح المصفوفات وسنوظّف هذه المعرفة في المقال التالي لتعلّم كيفية جمع [الأشعة](رابط المقال التالي). ترجمة -وبتصرُّف- للفصل Matrix Addition من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ المزيد المقال السابق الأشعة والنقاط والمصفوفات العمودية في الرسوميات الحاسوبية ثلاثية الأبعاد. أنواع البيانات والعمليات الأساسية في لغة بايثون.

سنناقش في هذا المقال كائنات الرسوميات الحاسوبية التي هي الأشعة والنقاط وكيفية تمثيلها في الحاسوب بوصفها مصفوفات عمودية، فالمصفوفة العمودية column matrix هي كائن رياضي له العديد من الاستخدامات إلى جانب استخدامه في الرسوميات الحاسوبية، ولكن سنتعرف في هذا المقال على كيفية استخدامها في الرسوميات الحاسوبية فقط. سنتعرّف في هذا المقال على المواضيع التالية: نمذجة وعرض الرسوميات الحاسوبية. النقاط والأشعة الهندسية. المصفوفات العمودية والسطرية. حساب الإزاحات. مساواة المصفوفات العمودية. أسماء المصفوفات العمودية وعناصرها. تمثيل النقاط باستخدام المصفوفات العمودية. تُعَد النقاط والأشعة الهندسية ضروريةً في الرسوميات الحاسوبية، ويجب تمثيلها بطريقة تسهّل التعامل معها، لذا تُعَد المصفوفة العمودية الخيار المعتاد لذلك. تستخدم بعض كتب الرسوميات مصطلح الشعاع العمودي Column Vector للتعبير عن الكائن الذي نسميه في مقالنا بالمصفوفة العمودية، إذ يُعَد ذلك مجرد اختلافٍ في المصطلحات ولا يؤثر على المفاهيم أو الصيغ التي سنوضّحها لاحقًا، ولكن المشكلة الأسوأ هي أن بعض الكتب تستخدم المصفوفات السطرية Row Matrices، فالمصفوفات العمودية والمصفوفات السطرية متكافئة، ولكن المعادلات المكتوبة باستخدام المصفوفات السطرية ليست هي نفسها المكتوبة باستخدام المصفوفات العمودية. يمكننا ضبط هذه الاختلافات، ولكنها مزعجة قليلًا. مثال مشهد السائح الافتراضي ما هما نوعا الكائنات الهندسية التي يمكن تمثيلها باستخدام المصفوفات العمودية؟ هما النقاط والأشعة. تتكون الرسوميات الحاسوبية من نشاطين: أولهما إنشاء عالم خيالي ثلاثي الأبعاد في الحاسوب، وثانيهما إنتاج صور ثنائية الأبعاد لذلك العالم من نقاط نظر مختلفة. يشبه برنامج الرسوميات السائحَ الذي يتجول في معالم طبيعية رائعة ويلتقط الصور بالكاميرا، ويُجهَّز السائح الافتراضي بكاميرا سينمائية مع الرسوم المتحركة الحاسوبية. يتكون المشهد الخيالي من كائنات في فضاء ثلاثي الأبعاد، ويُحدَّد كل كائن باستخدام النقاط والخطوط التي تقع على سطحه مثل المشهد الشتوي السابق لصاحبه توان فان Tuan Phan. يتكون هذا النموذج من نقاط وقطع مستقيمة تربط بينها، وهناك حاجة إلى مزيدٍ من العمل لملء المنطقة بين القطع المستقيمة ولتطبيق الإضاءة للحصول على صورة واقعية. صورة المشهد الكاملة هل يمكن تمثيل الكرة باستخدام النقاط والخطوط؟ نعم، بالتأكيد. انظر إلى جسد رجل الثلج، إذ يبدو الشكل وكأنه كرة عند ملء المضلعات. هذه هي الصورة الكاملة، مع ملء المضلعات وتطبيق الإضاءة وإلقاء قليلٍ من ندف الثلج. يمكنك طلب نماذج من الكرات والأسطوانات والأقماع ووضعها في مشهدك في المكان الذي تريده باستخدام حزم الرسوميات الحاسوبية ثلاثية الأبعاد مثل OpenGL التي تملأ أيضًا المضلعات تلقائيًا وتطبّق نموذج الإضاءة لإنتاج تظليل واقعي. مشهد افتراضي آخر هل يمكن لسائحنا الافتراضي أن يتجول في مشهد الثلوج الافتراضي ويلتقط صورة مختلفة؟ نعم، يمكنه ذلك. يضع نموذج المشهد الثلجي كائنات مختلفة في فضاء ثلاثي الأبعاد، وبالتالي يمكن لسائحنا الافتراضي أن يتجول على يمين رجل الثلج ويلتقط صورةً أخرى ثنائية الأبعاد باستخدام الكاميرا الافتراضية، إذ أُنتِجت الصورة السابقة باستخدام النموذج والإضاءة نفسها، ولكن مع وضعٍ مختلف للكاميرا. الشعاع Vector ما هي النقطة؟ وضحنا في المقال السابق مفهوم النقطة بأنها موقع في الفضاء، حيث تُعَد النقطة في الهندسة موقعًا في الفضاء فليس لها حجم وخاصيتها الوحيدة هي الموقع، بينما تكون النقطة عادةً في الرسوميات الحاسوبية هي رأس الشكل ثلاثي الأبعاد. أما الشعاع الهندسي فله خاصيتان: الطول والاتجاه، ولكن ليس له موقع ثابت في الفضاء، فإذا كان له موقع ثابت، فسيكون قطعة مستقيمة. قد يكون الحديث عن شيء ليس له موقع أمرًا غريبًا، ولكنه يسهّل تطبيق الرسوميات الحاسوبية ثلاثية الأبعاد. يسمى هذا المزيج من "المسافة والاتجاه" بالإزاحة Displacement أحيانًا، ويمكن تطبيق الإزاحة نفسها (أي إزاحة واحدة فقط) على كل نقطة من النقاط المختلفة. لنفترض أن لدينا المكعب التالي مثلًا، إذ يحتوي الوجه الأمامي على أربعة رؤوس (أربع نقاط). إذا تحركتَ من كل نقطة من هذه النقاط بمقدار المسافة والاتجاه نفسه، فستصل إلى النقاط الأربعة للوجه الخلفي. تمثل العبارة "المسافة والاتجاه نفسه" الشعاعَ الذي يظهر بوصفه خطًا مع رأس سهم، ويوضح الشكل التالي هذا الشعاع أربع مرات، مرة واحدة لكل نقطة من الوجه. المصفوفة العمودية لنفترض أنك قضيت عطلة الربيع على الشاطئ والشمس مشرقة، فهل يسطع ضوء الشمس في الاتجاه نفسه لكل الموجودين على الشاطئ؟ نعم، إذ يكون "الاتجاه نحو الشمس" نفسه لكل الموجودين على الشاطئ، وبالتالي فهو شعاع. نهتم أحيانًا بالاتجاه فقط دون الاهتمام بالموقع أو بالطول كما في السؤال السابق، لذا نستخدم الشعاع لهذا الغرض، فطوله ليس مهمًا، لأننا نستخدم طولًا واحدًا في كثير من الأحيان. نهتم في أحيانٍ أخرى بكلٍ من الاتجاه والحجم، وعندها يُستخدَم كلٌّ من اتجاه وطول الشعاع. يمكن تمثيل الشعاع بقائمةٍ من الأعداد تدعى المصفوفة العمودية، والتي هي قائمة مرتبة من الأعداد المكتوبة ضمن عمود. تستخدم بعض الكتب كلمة "شعاع" لتعبّر عن فكرة الشعاع وتمثيله بوصفه ترتيبًا لثلاثة أعداد، ولكن يمكن أن يكون ذلك مربكًا أحيانًا. إليك فيما يلي مثالًا لمصفوفة عمودية: يسمى كل عددٍ في المصفوفة العمودية عنصرًا Element، وتكون هذه الأعداد حقيقية real، ويسمى عدد العناصر في الشعاع بالبُعد Dimension. المصفوفة السطرية Row Matrix هي قائمة مرتبة من الأعداد المكتوبة في صف واحد مثل المصفوفة السطرية: ‎(12.5, -9.34)‎. سنمثّل الأشعة دائمًا باستخدام مصفوفات عمودية بهدف التناسق، وتمثل بعض الكتب الأشعة باستخدام مصفوفات سطرية، إذ لا يحدث ذلك فرقًا جوهريًا، ولكنه يغيّر بعض الصيغ الرياضية قليلًا. ما هو عدد العناصر الموجودة في كل مصفوفة عمودية؟ الجواب هو: استخدام المتغيرات بوصفها عناصر مصفوفة يمكن أن تكون عناصر المصفوفة العمودية متغيرات variables كما يلي: يُعطَى العنصر الأول في المصفوفة العمودية أحيانًا الفهرس "0" أوالفهرس "1" أحيانًا. العرض المناسب للمصفوفة العمودية هل المصفوفة العمودية التالية: هي المصفوفة العمودية التالية نفسها؟ لا يمكن ذلك، فالمصفوفة العمودية هي قائمة مرتبة من الأعداد، وهذا يعني أن كل موضع في المصفوفة العمودية يحتوي على عدد أو متغير معين. يُعَد مظهر المصفوفات العمودية غريبًا في النصوص المطبوعة، لذا من الشائع كتابتها كما يلي: ‭(2.9, -4.6, 0.0)‎ T يرمز الحرف "T" إلى منقول المصفوفة Transpose الذي يعني تحويل الصفوف إلى أعمدة (سنوضح لاحقًا بالتفصيل معنى المنقول). المساواة بين المصفوفات هل المصفوفة ‎(1.2, -3.9, 0.0)‎ تساوي المصفوفة ‎(1.2, -3.9, 0.0)T‎؟ لا، فالمصفوفة الأولى هي مصفوفة سطرية، والمصفوفة الثانية هي مصفوفة عمودية، أي مكتوبة ضمن صف، ولكن الحرف "T" يعني أنها مصفوفة عمودية، إذ تُعَد المصفوفات السطرية والمصفوفات العمودية أنواعًا مختلفة من الكائنات، ولا يمكن أن تكون متساوية. ربما لم نميّز سابقًا بين المصفوفات السطرية والمصفوفات العمودية، ولم نوضِّح اختلاف الأشعة الهندسية عن المصفوفات العمودية المستخدمة لتمثيل هذه الأشعة، إذ يمكن أن تبدو هذه الاختلافات صعبة حاليًا، ولكن أبقِها حاضرةً في ذهنك لتجنب الالتباس مستقبلًا. يمكن أن تكون المصفوفتان العموديتان متساويتين إذا كانت: كلتا المصفوفتين مصفوفةً عمودية. لكل منهما البعد (عدد العناصر) نفسه. العناصر المقابلة لبعضها البعض في المصفوفتين متساوية. يمكن أن تكون المصفوفتان السطريتان متساويتين إذا كان: كلتا المصفوفتين مصفوفات سطرية. لكل منهما البعد (عدد العناصر) نفسه. العناصر المقابلة لبعضها البعض في المصفوفتين متساوية. الفروق الدقيقة بين المصفوفات هل المصفوفتان السطريتان ‎(8.0, -1.63, 7.0, 0.0)‎ و ‎(8.0, -1.63, 7.0, 1.0)‎ متساويتان؟ لا. يمكن مقارنة المصفوفات من النوع نفسه فقط، إذ يمكنك المقارنة بين مصفوفتين عموديتين ثلاثيتي الأبعاد، أو مصفوفتين سطريتين رباعيتي الأبعاد مثلًا، فليس من المنطقي مقارنة مصفوفة سطرية ثلاثية الأبعاد مع مصفوفة عمودية ثلاثية الأبعاد. ‭( 6, 8, 12, -3 )T = ( 6, 8, 12, -3)T ‭( 6, 8, 12, -3 ) = ( 6, 8, 12, -3 ) ‭( 6, 8, 12, -3 ) ≠ ( -2.3, 8, 12, -3 ) ‭( 6, 8, 12, -3 )T ≠ ( 6, 8, 12, -3 ) ‭( 6, 8, 12, -3 )T ≠ ( 6, 8, 12 )T يمثل المحرف ≠ عدم المساواة (قد يكون من الصعب رؤيته باستخدام متصفح الويب). تكون القواعد أحيانًا مريحة وتؤدي إلى عدم الدقة في التمييز بين المصفوفات السطرية والمصفوفات العمودية، ولكن سيؤدي إبقاء التمييز بينها واضحًا إلى تجنب الارتباك مستقبلًا. هل تُعَد المصفوفتان العموديتان ‎(1.53, -0.03, 9.03, 0.0, +8.64)T‎ و ‎(1.53, -0.03, 9.03, 1.0, -8.64)T‎ متساويتين؟ لا، ليستا متساويتين. أسماء المصفوفات من المفيد أن يكون للمصفوفات أسماء، إذ يُستخدَم عادةً حرف صغير بخط عريض لمصفوفة سطرية أو عمودية كما يلي: a = ( 1.2, -3.6 ) x = ( x1, x2, x3, x4 ) r = ( r0, r1 )T من المعتاد استخدام الأسماء من بداية أحرف الأبجدية الإنجليزية للمصفوفات العمودية التي تكون عناصرها معروفة مثل المصفوفة a السابقة، واستخدام الأسماء من نهاية أحرف الأبجدية الإنجليزية للمصفوفات العمودية التي تكون عناصرها متغيرات. تكون أسماء عناصر المصفوفة العمودية غالبًا مؤلفة من اسم المصفوفة العمودية الكاملة مع رمز سفلي مثل المصفوفة العمودية r وعناصرها r0‎ وr1‎. من الصعب كتابة الأحرف ذات الخط العريض بالقلم الرصاص أو بالطباشير، لذا بدلًا من ذلك يُوضَع سهم أو شريط فوق اسم المصفوفة العمودية كما يلي: _ -> x x لنفترض أن لدينا ما يلي: x = ( x1, x2 ) y = ( 3.2, -8.6 ) x = y ما الذي يجب أن يكون صحيحًا بشأن x1‎ و x2‎؟ x1 = 3.2 و x2 = -8.6 تمثيل الأشعة باستخدام المصفوفات العمودية تُستخدَم المصفوفات العمودية لتمثيل الأشعة وتُستخدَم لتمثيل النقاط أيضًا. يُستخدَم في الفضاء ثنائي الأبعاد نوع البيانات نفسه -وتكون مصفوفات عمودية ثنائية الأبعاد- لتمثيل نوعين مختلفين من الكائنات الهندسية هما النقاط والأشعة، ويُعَد ذلك أمرًا مربكًا، لذا سنصحح هذا الوضع لاحقًا. يوضح الشكل السابق شعاع الإزاحة الذي يمثل الفرق بين نقطتين في المستوي x-y، إذ نستخدم حاليًا أمثلةً في فضاء ثنائي الأبعاد، وسيأتي الفضاء ثلاثي الأبعاد لاحقًا. النقطة A لها الإحداثيات: x=2 و y=1، ويمكن تمثيلها بمصفوفة عمودية: ‎(2, 1)T‎. النقطة B لها الإحداثيات: x=7 و y=3، ويمكن تمثيلها بمصفوفة عمودية: ‎(7, 3)T‎. يمكن حساب الإزاحة من النقطة A إلى النقطة B في مسألتين منفصلتين هما: الإزاحة x هي الفرق بين قيم X أي: ‎7-2 = 5. الإزاحة y هي الفرق بين قيم Y أي: 3‎-1 = 2. وشعاع الإزاحة المُعبَّر عنه بمصفوفة هو: ‎(5, 2)T‎ = d‎. تُصوَّر أشعة الإزاحة على شكل سهم يربط بين نقطتين، إذ تكون النقطة A هي ذيل الشعاع، والنقطة B هي رأس الشعاع في الرسم البياني، ولكن تذكّر أن الأشعة ليس لها موضع، لذا يُعَد هذا الرسم مجرد مكان مناسب لرسمها، ولا يعبّر عن موضعها. الإزاحة Displacement تمثل المصفوفة العمودية d شعاع الإزاحة من النقطة A إلى النقطة B، فما هي المصفوفة العمودية التي تمثل الإزاحة من النقطة B إلى النقطة A؟ الإزاحة من النقطة B إلى النقطة A هي: الإزاحة x هي: 2‎-7 = ‎-5 الإزاحة y هي: 1‎-3 = ‎-2 وبالتالي فإن المصفوفة العمودية التي تمثل الإزاحة هي: ‎(-5, -2)‎T‎ = e‎ يؤشر شعاع الإزاحة إلى الاتجاه المعاكس عند زيارة النقاط بالترتيب المعاكس، ويكون كل عنصر ناتجًا عن ضرب القيمة القديمة بالعدد ‎-1 في المصفوفة العمودية. تختلف الإزاحة من النقطة A إلى النقطة B عن الإزاحة من النقطة B إلى النقطة A، إذ يمكن التفكير في الإزاحة بوصفها "إرشادات حول كيفية المشي من نقطة إلى أخرى"؛ لذا إذا كنت واقفًا عند النقطة A وترغب في الوصول إلى النقطة B، فإن الإزاحة ‎(5, 2)‎T‎ تقول "امشِ 5 وحدات في الاتجاه الموجب X، ثم امشِ وحدتين في الاتجاه الموجب Y". تحتاج بالطبع إلى اتجاهات مختلفة للانتقال من النقطة B إلى النقطة A، حيث تقول الإزاحة ‎(-5, -2)‎T‎ "امشِ 5 وحدات في الاتجاه السالب X، ثم امشِ وحدتين في الاتجاه السالب Y"، مما يعيدك إلى النقطة A. يمكن التعبير عن الإزاحة من نقطة البداية إلى نقطة النهاية كما يلي: الإزاحة = ‎‪(x نقطة النهاية - x نقطة البداية, y نقطة النهاية - y نقطة البداية)‎T‎ لنفترض أن النقطة C هي: x=4, y=2 وأن النقطة D هي: x=3, y= 5، فما هي المصفوفة العمودية التي تمثل الإزاحة من C إلى D؟ X لنقطة النهاية - X لنقطة البداية = 3 - 4 = ‎-1 Y لنقطة النهاية - Y لنقطة البداية = 5 - 2 = 3 إذًا فالمصفوفة العمودية هي: ‎(-1, 3)‎T‎ قراءة الإزاحات من الرسوم البيانية الورقية يوضح الرسم البياني التالي شعاعًا بين نقطتين، حيث يمكن قراءة عناصر الإزاحة بين النقطتين من الرسم البياني من خلال حساب عدد المربعات من ذيل الشعاع إلى رأسه: ‎(-3, 5)‎T‎. افعل الشيء ذاته الآن مع الرسم البياني التالي: ما هي الإزاحة من النقطة E إلى النقطة F؟ الإزاحة هي: ‎(7, 3)‎T‎ للتحقق من إجابتك، ابدأ من نقطة البداية واتبع التعليمات التالية: امشِ بمقدار 7 وحدات على محور X، ثم امشِ بمقدار 3 وحدات على محور Y. إذا كانت إجابتك صحيحة، فسينتهي بك الأمر عند نقطة النهاية. ليس للأشعة موقع محدد ما هي الإزاحة من النقطة G: (-3, 4)‎T‎ إلى النقطة H: (5, -2)‎T‎؟ يمكن الإجابة على هذا السؤال من خلال طرح قيم نقطة البداية G من القيم المقابلة لنقطة النهاية H ويعطي ذلك: ‎(8, -6)‎T‎. احسب الآن الإزاحة من النقطة M إلى النقطة N في الرسم البياني التالي من خلال طرح قيم نقطة البداية N من القيم المقابلة لنقطة النهاية M، ويعطي ذلك: ‎(8, -6)‎T‎، وهي القيمة نفسها للرسم البياني السابق. يُعَد شعاع الإزاحة هندسيًا من النقطة G إلى النقطة H هو شعاع الإزاحة نفسه من النقطة M إلى النقطة N، وتكون المصفوفتان العموديتان متساويتين باستخدام قاعدة مساواة المصفوفات العمودية. يُعَد ذلك منطقيًا، لأنك تقطع المسافة والاتجاه نفسه للمشي من النقطة M إلى النقطة N عند المشي من النقطة G إلى النقطة H، وبالتالي توضح هذه الرسوم البيانية الإزاحات مع الطول والاتجاه نفسه ولكن مع نقاط بداية مختلفة، فليس للأشعة موقعٌ محدد. من الشائع رسم الشعاع على شكل سهم في الرسوم البيانية، ذيله عند نقطة ورأسه عند نقطة أخرى، ولكن يمكن أن يمثل أيّ سهم له الطول والاتجاه نفسه هذا الشعاع. طرح النقاط هل تُعَدّ الإزاحة بين نقطتين فريدة؟ نعم، هذا صحيح. يمكن كتابة صيغة حساب شعاع الإزاحة على النحو التالي، إذ تساوي الإزاحة من النقطة S (نقطة البداية) إلى النقطة F (نقطة النهاية) ما يلي: F - S = ( Xf , Yf )T - ( Xs , Ys )T = ( Xf-Xs , Yf-Ys )T تُستخدَم نقطتان في هذه العملية لإنتاج شعاع واحد، فمن الغريب أن ينتج عن طرح كائنين لهما النوع نفسه كائنٌ من نوع آخر، وهذا يقودنا إلى السؤال التالي: إذا طرحنا نقطةً ثلاثية الأبعاد من نقطة أخرى ثلاثية الأبعاد، فهل ستكون النتيجة شعاعًا؟ نعم، إذ تعمل هذه الطريقة في الفضاء ثلاثي الأبعاد وثنائي الأبعاد. تدريب عملي لحساب الإزاحة لنفترض أن النملة ريم ضاعت عند النقطة ‎(8, 4)‎T‎، فأوجد الإزاحة التي ستوصِلها إلى صديقتها سلمى عند النقطة ‎(2, 2)‎T‎، أو ما هي الإزاحة التي يجب أن تتحرك بها ريم للعثور على صديقتها سلمى؟ لنطرح النقاط (سلمى - ريم): ‎(2, 2)‎T‎ - (8, 4)‎T‎ = (-6, -2)‎T‎ ستحصل على الإجابة نفسها من خلال عدّ مربعات ورقة الرسم البياني. استخدام الأعداد الحقيقية قد نرغب في تجنب الأعداد السالبة وبالتالي سنحسب الإزاحة بصورة غير صحيحة، إذ يُعَد وجود إزاحات سالبة أمرًا طبيعيًا، فالجزء "السلبي" مطلوب لإظهار الاتجاه. شيء آخر يجب أخذه في الحسبان وهو أن عناصر المصفوفة العمودية هي أعداد حقيقية، ولكن استخدمنا في الأمثلة أعدادًا صحيحة لتسهيل الأمور فقط، فلا يوجد أيّ خطأ في المصفوفة العمودية ‎(-1.2304, 9.3382)‎T‎. لنفترض أن لدينا النقطتان: النقطة B وهي: ‎( 4.75, 6.23 )‎ والنقطة A وهي: ‎( 1.25, 4.03 )‎، فما هي الإزاحة من النقطة A إلى النقطة B؟ الإزاحة من النقطة A إلى النقطة B هي: ‭( 4.75, 6.23 ) - ( 1.25, 4.03 ) = ( 3.50, 2.20 )T وصلنا إلى نهاية هذا المقال، وسنناقش في المقال التالي العمليات على الأشعة والعمليات المكافئة باستخدام المصفوفات العمودية. ترجمة -وبتصرُّف- للفصل Vectors, Points, and Column Matrices من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ المزيد المقال السابق التعرف على النقاط والخطوط في الرسوميات الحاسوبية ثلاثية الأبعاد. الرسم باستخدام الأدوات المساعدة في كريتا دليلك الشامل إلى أنواع البيانات.

سنوضح في هذا المقال الأدوات الرياضية المُستخدَمة في الرسوميات الحاسوبية ثلاثية الأبعاد Three Dimensional Computer Graphics -أو 3D Graphics اختصارًا، إذ يبني برنامج الرسوميات ثلاثية الأبعاد مشهدًا مكونًا من كائنات ثلاثية الأبعاد في فضاء ثلاثي الأبعاد، ثم تُنتَج صور ثنائية الأبعاد من المشهد ثلاثي الأبعاد، ويُمثَّل المشهد بوصفه هيكل بيانات في ذاكرة الحاسوب، وتُعَد الصورة ثنائية الأبعاد عادةً هي الصورة الموجودة على واجهة شاشة الحاسوب. تتكون الكائنات ثلاثية الأبعاد من نقاط وخطوط ومضلعات، إذ لا بد أنك تعرف ماهية هذه المفاهيم، ولكننا سنوضح في هذا المقال هذه المفاهيم ونقدم بعض المفردات الخاصة بالرسوميات الحاسوبية حتى نبدأ من أرضية مشتركة، إذ سنتعرّف على المواضيع التالية: النقاط. الخطوط. المثلثات. تمثيل النقاط والخطوط. إطارات الإحداثيات. تحديد الإحداثيات. تأثير تغيير الإطارات على الإحداثيات. الأشعة. تمثيل الأشعة. هناك شيئان أساسيان في الهندسة هما النقاط والخطوط، إذًا لنتعرف على هذين المفهومين، ولكن لنبدأ بالإجابة على سؤال "ما هي النقطة؟". النقطة ما هي النقطة؟ النقطة هي موقع في الفضاء. النقطة الهندسية هي موقع في الفضاء بدون أيّ خصائص أخرى، إذ لا تملك طولًا أو عرضًا أو سماكة، وتعَد موقعًا مجردًا. لن يساعدك هذا التعريف لمفهوم النقطة إن لم يكن لديك فهمٌ مسبق له، إذ تشير عبارة "موقع في الفضاء" إلى مفهوم كلمة "نقطة" نفسه، ولا يمكن للتعريف أن ينقل لك مفهومًا لا تملكه مسبقًا. لا يوجد تعريف لكلمة نقطة في الهندسة، فالنقطة هي إحدى المفاهيم الأولية غير المُعرَّفة التي تُستخدَم لتعريف الكائنات الأخرى، إذ تعطي الكتب أمثلةً عنها وتأمل أن تبني بنفسك مفهومًا منها بطريقةٍ ما بدلًا من إعطائك تعريفًا لها. تُظهر الصورة التالية قبتين على أحد المباني، وتُعَد هذه الصورة ثنائية الأبعاد، لكن فكّر في المبنى الفعلي ثلاثيّ الأبعاد، وركّز على القضيب المعدني (النهائي) الموجود أعلى القبة الأقرب. إذًا، تحدّد النهايةُ الحادة للقضيب المعدني موقعًا دقيقًا بحسب مقياس المبنى، إذ يمكننا تصور هذا الموقع بوصفه نقطة. ما هي النقاط فيزيائيا؟ لنفترض أن هذا القضيب المعدني أمامك على مكتبك، فهل تُعَد نهايته نقطة؟ غالبًا لا، إذ تكون النهاية غير حادة جدًا بحسب هذا المقياس، بحيث لا يمكن عدّها نقطة. تعبّر النقطة عن المثالية، إذ تكون نهاية القضيب المعدني بحسب مقياس المبنى صغيرةً بما يكفي لعَدّها موقعًا محددًا، وبالتالي يمكن عدّها نقطة، ولكن تكون نهايته غير حادة جدًا بحسب مقياس مكتبك بحيث لا يمكنها تحديد موقع واحد فعلًا. يجب أن يتناقص حجم هذا القضيب المعدني إلى حجم الدبوس بحسب مقياس المكتب، وبالتالي يمكنك أن تحدّد نهايته نقطةً ما. لكن إذا وضعت الدبوس تحت المجهر، فستكون نهايته غير حادة جدًا بالنسبة لهذا المقياس مرة أخرى، وبالتالي يجب أن تتقلص أكثر إلى حجم البكتيريا مثلًا قبل أن تتمكن النهاية من تحديد نقطة ما، لكن أصبحت نهاية القضيب المعدني مرةً أخرى سميكةً جدًا بحسب مقياس البكتيريا بحيث لا يمكنها تحديد الموقع بدقة. إذًا تعبّر النقاط في الفضاء ثلاثي الأبعاد عن المثالية، إذ تكون النهاية الحادة للقضيب المعدني دقيقةً بما يكفي لتكون نقطة بالنسبة لنموذج المبنى الحاسوبي، ولا يلزم تحديد الحواف والمستويات والأشكال الأخرى التي يتكون منها المبنى بدقة أكبر. النقاط في الفضاء ما هو موقع نهاية القضيب المعدني الأبعد في الفضاء؟ انظر إلى الصورة مرةً أخرى وتخيل العلاقة بين نقطتي نهايتي القضيبين المعدنيين، إذ لا توجد إجابة فعلية ضرورية حاليًا. تكون نقاط النهاية للقضيبين المعدنيين في مواقع محدّدة من العالم الحقيقي real world، وسنحدّد هذه المواقع باستخدام إطار إحداثي لاحقًا، ولكن لنفكر الآن فقط في النقاط الموجودة في الفضاء. تضع في برامج الرسوميات ثلاثية الأبعاد نقاطًا وخطوطًا وأشياءً أخرى في الفضاء، ثم تسقطها على صورة ثنائية الأبعاد، ويحاكي ذلك ما حدث عند إنتاج الصورة باستخدام الكاميرا، إذ تكون نهايات القضيبين المعدنيين فيزيائيًا نقاطًا في الفضاء ثلاثي الأبعاد. تسقط العدسة كامل المشهد على مستشعر الصور ثنائية الأبعاد، وتحدد نهايات القضبان المعدنية في الصورة ثنائية الأبعاد نقطتين ثنائيتي الأبعاد. الخطوط ما المسافة بين النقطتين عند طرفي القضيبين المعدنيين؟ يمكن أن نخمن أن المسافة حوالي 30 مترًا. يكون الحكم على العمق صعبًا في الصورة ثنائية الأبعاد في أغلب الأحيان، إذ تُفقَد معلومات العمق عند إنتاج صورة ثنائية الأبعاد من مشهد ثلاثي الأبعاد (إما مشهد حقيقي أو مشهد في الحاسوب). فكر الآن في القطعة المستقيمة Line Segment الواقعة بين النقطتين، والتي هي المسار المستقيم بين نقطتين بدون سماكة، ولا توجد سوى قطعة مستقيمة واحدة بين النقطتين. إن لم يكن لديك مفهوم مسبق عن "الخط"، فلن يكون التعريف السابق كافيًا لتعلمه، إذ تشير عبارة "المسار المستقيم" إلى مفهوم الخط الذي عرّفناه. تتعامل غالبًا مع القطع المستقيمة في الرسوميات ثلاثية الأبعاد، بينما تستمر الخطوط بلا نهاية في الهندسة، إذ تكون القطعة المستقيمة جزءًا من الخط بين نقطتين. لا يُعرَّف الخط العالمي في كتب الهندسة عادةً، وهو -مثل النقطة- مفهوم غير مُعرَّف يستخدم لتعريف كائنات أخرى، إذ تقدّم الكتب صورًا وأمثلة عن الخطوط، وتأمل أن تفهم بطريقة أو بأخرى ما هو الخط من خلال النظر إليها. يستخدم بعض الأشخاص مصطلح "خط" بينما يجب عليهم استخدام مصطلح "قطعة مستقيمة" الذي سنستخدمه في هذا المقال، نظرًا لأن القطع المستقيمة شائعة جدًا. القطع المستقيمة هل يمكنك تمديد stretch طول السلك بين النقطتين؟ نعم، من الناحية المفاهيمية على الأقل. يوجد سلك رفيع ممتد بين القضيبين المعدنيين بحسب مقياس المبنى، والذي يعبر عن تقريبٍ لقطعة مستقيمة، وكما تعلم يتعلق هذا الأمر بالمقياس، إذ يُرجَّح أن يكون السلك أسمك من الخط المرسوم بقلم رصاص، فالسلك الموجود على مكتبك سميك جدًا بحيث لا يمكن عدّه قطعة مستقيمة. بينما يكون الخط المرسوم بقلم الرصاص الرفيع والمستقيم رفيعًا بدرجة كافية لعدّه خطًا هندسيًا، وإذا كان سميكًا جدًا، فيمكن أن يكون طول خيط العنكبوت الممتد بين نقطتين مناسبًا. لكن يمكن عَدّ الأسلاك المدروسة على المستوى المعماري بمثابة قطع مستقيمة، ويمكنك بناء نموذج هندسي للمبنى باستخدام القطع المستقيمة لتمثيل الحواف. المثلثات جرّب رسم مثلث يربط بين القضيبين المعدنيين والزاوية العلوية اليسرى من السور الأبيض كما في الصورة التالية: يمكن إنشاء المثلث من خلال ربط ثلاث نقاط في فضاء ثلاثي الأبعاد بقطع مستقيمة، فإذا لم تقع النقاط الثلاث جميعها على الخط نفسه، فستحدّد ثلاث نقاط في الفضاء مثلثًا فريدًا. تُعَد المثلثات الموجودة في الفضاء مهمةً في الرسوميات ثلاثية الأبعاد، إذ تُنشَأ الكائنات ثلاثية الأبعاد التي تشكّل المشهد من المثلثات والمضلعات المسطحة الأخرى. المثلث الموجود في الصورة ثنائية الأبعاد هو إسقاط للمثلث ثلاثي الأبعاد في المشهد، ولكن يشوه الإسقاطُ المثلثَ ثلاثيّ الأبعاد، فالمثلث ثلاثي الأبعاد أكبر بكثير من المثلث ثنائي الأبعاد، وتكون الزوايا مختلفة. لنفترض أن الكائن ثلاثي الأبعاد في المشهد مكونٌ من عدة مثلثات، ولنسقط كل مثلث على صورة ثنائية الأبعاد، والنتيجة هي النسخة المُسقَطة من الكائن ثلاثي الأبعاد. يتكون السور الشبكي الأبيض في المبنى من العديد من المثلثات، وتُظهِر نسخة السور الشبكي الموجودة في الصورة جميع هذه المثلثات التي تسقطها عدسة الكاميرا. التمثيل باستخدام إطار إحداثيات هل تحتاج إلى إطار إحداثي -أي نظام مع تسمية النقاط بالإحداثيات x و y و z- للحديث عن النقاط والخطوط والأشكال المستوية؟ في الحقيقة لا حاجة لذلك. يمكنك التفكير في النقاط والخطوط والأشكال المستوية التي تشكّل المشهد ثلاثي الأبعاد دون استخدام نظام إحداثي، وهذا ما كنا نفعله في الحقيقة، ولكن يجب تمثيل هذه الكائنات بطريقة أو بأخرى والتعامل معها في رسوميات الحاسوب، ولذلك نحتاج إلى طريقة لتمثيلها. اختر نقطةً مناسبة في المشهد ثلاثي الأبعاد وأطلِق عليها اسم نقطة الأصل Origin، وحدد ثلاثة خطوط تسمى X و Y و Z والتي تمر عبر نقطة الأصل، وتكون الخطوط الثلاثة عادةً متعامدة على بعضها بعضًا، ويسمى كل خط محورًا Axis. اختر اتجاهًا إيجابيًا لكل خط، فهناك عدة خيارات لذلك، ولكن لنستخدم الخيار الموضّح في الصورة السابقة. تمثل كل نقطة من المحور X مسافةً فريدةً (موجبة أو سالبة أو صفر) من نقطة الأصل، فمثلًا تقع زاوية المبنى الموجودة على المحور X على مسافة 2.4 متر (8 أقدام) تقريبًا من نقطة الأصل. الإحداثيات تقع نقطة الأصل على ارتفاع صفر، ولكن على أي ارتفاع تقع نقطة نهاية القضيب المعدني الأقرب تقريبًا؟ يمكن القول أن ارتفاعها حوالي 3.6 مترًا (10 أقدام). أو يمكنك القول أن y=3.6 بالنسبة لنقطة نهاية القضيب المعدني، إذ يمكن إسناد تمثيل لأيّ نقطة في مشهدنا ثلاثيّ الأبعاد من خلال قياس المسافة على طول المحاور الثلاثة، إذ سنضع هذه المسافات الثلاث في مصفوفة عمودية على النحو التالي في هذا المقال (وفي العديد من كتب الرسوميات الحاسوبية): قد تكون معتادًا على وضع الإحداثيات الثلاثة في صف ثلاثي مثل (x, y, z)، ولكن سيتبين أنه من الملائم أكثر وضعها في مصفوفة عمودية كما ذكرنا بالنسبة للرسوميات الحاسوبية، فمثلًا إحداثيات زاوية المبنى التي تقع على طول المحور X هي تقريبًا: تحديد الإحداثيات ما هي إحداثيات نقطة زاوية الشبكة البيضاء على طول الحافة العلوية (المسمَّاة P0)؟ يمكن القول أنها تقريبًا: احسب عند تحديد الإحداثيات قياس المسافة على طول الخطوط الموازية لمحاور الإحداثيات، إذ ستشكّل الخطوط التي تستخدمها مستطيلًا أو أوجه صندوق. تشكّل الخطوط السوداء المنقطة المستخدمة للنقطة Q0 مستطيلًا، ويعطي قياس أضلاع المستطيل الإحداثيات التالية: من الصعب معرفة إحداثيات النقطة Q1، فالصورة ثنائية الأبعاد، ولكن المشهد الذي تظهره ثلاثي الأبعاد، وبالتالي فإن المحور Z مشوه، ولكن تشكل الخطوط المنقطة في المشهد ثلاثي الأبعاد صندوقًا، فقياس جميع الزوايا 90 درجة. مزيد من النقاط يمكن تقدير إحداثيات النقطة Q1 بالقيم التالية: لنعُد الآن إلى مشهدنا الواقعي، إذ يبلغ طول الشبكة البيضاء تقريبًا حوالي 2.4 متر (8 أقدام) من كل جانب. النقطة وتمثيلها يمكن تخمين إحداثيات طرف القضيب المعدني الأقرب بالقيم التالية: تُعَد المصفوفة العمودية كائنًا رياضيًا يمثل النقطة باستخدام إطار الإحداثيات الذي اخترناه، ولكن ليست هذه المصفوفة العمودية هي النقطة بحد ذاتها، فالمصفوفة العمودية والنقطة شيئان مختلفان، إذ يُستخدَم أحدهما لتمثيل الآخر مثل استخدام اسمك لتمثيلك. نأمل أن يكون ذلك واضحًا، ولكنه سيكون غامضًا بالنسبة للطلاب الذين يحاولون تخطي مواضيع رياضيات الرسوميات الحاسوبية بسرعة، مما يؤدي إلى ندمهم في نهاية المطاف، إذ يمكن أن يمثل كتاب الرسوميات الحاسوبية النقطة نفسها بعدة طرق مختلفة، لذا من الضروري الفصل بين أفكار النقطة الهندسية والطرق المتعددة التي يمكن تمثيلها باستخدامها. ملاحظة: يتحدث الأشخاص في أغلب الأحيان عرضيًا ويقولون أشياء مثل "النقطة ‎(4, 12, -4)‎"، كما لو كان هذا الصف الثلاثي من الأرقام متطابقًا مع النقطة، ولكن يُستخدَم ذلك للراحة فقط، إذ ينبغي عليهم أن يقولوا: "النقطة المُمثَّلة في نظام الإحداثيات الذي اخترناه بالتمثيل ‎(4, 12, -4)‎." تأثير تغيير الإطارات على الإحداثيات هل تقاس المسافات على طول محاور الإحداثيات بوحدة القدم أم بالأمتار؟ لا يهم، طالما أنك تستخدمها بصورة متناسقة. لا تُوضَع إطارات الإحداثيات المستخدمة في كتب الرياضيات في مشهد من العالم الحقيقي عادةً، لذلك لا يُعبَّر عن المسافات بأيّ وحدة معينة، ولكن يتعين عليك تحديد الوحدات التي تستخدمها عندما تنشئ عالمًا ثلاثي الأبعاد في الحاسوب. تُظهر الصورة التالية عالمًا ثلاثيّ الأبعاد مع وضع إطارٍ إحداثي مختلف فيه، إذ تبقى النقاط في العالم نفسها كما كانت سابقًا، ولكن سيكون لديها تمثيلات مختلفة مع إطار إحداثي مختلف: مثلنا النقطة المسمَّاة P1 بما يلي في الإطار السابق: ستكون الآن المسافات على طول المحاور في الإطار الجديد (الأخضر) مختلفة، فالمصفوفة العمودية التي تمثل النقطة P1 في الإطار الجديد هي تقريبًا: لم نمارس الرياضيات بصورة دقيقة هنا، بل نظرنا إلى الصورة وخمّنا المسافات فقط، لذا حاول أن تفعل الشيء نفسه، فالهدف ليس حساب أي شيء، بل التفكير في النقاط في الفضاء. للنقطة نفسها تمثيلات مختلفة في كل إطار، لذا يجب أن تعرف الإطار المُستخدَم عندما تمثل نقطةً بمصفوفة عمودية. ضوء الشمس يمكن تقدير إحداثيات النقطة P0 على الحافة العلوية للشبكة المبينة في الصورة أعلاه بالمصفوفة العمودية التالية: ولكن هذه القيم مجرد تقدير فقط. انظر إلى صورة المبنى مرةً أخرى، إذ تضيء الشمسُ المشهد، ولكنها ليست موجودة في الصورة، إذ يأتي ضوء الشمس في المشهد قطريًا من خارج المشهد إلى يساره. الأشعة Vector ارسم ذهنيًا بعض الخطوط في الصورة التي تظهر ضوء الشمس كما في الشكل التالي: يتدفق الضوء من أعلى اليسار عندما تنظر إلى المبنى، إذ تمثل الصورة ضوء الشمس بأسهم. حاول التفكير في المشهد ثلاثي الأبعاد بالرغم من أن الصورة ثنائية الأبعاد، فالاتجاه الذي يتحرك فيه الضوء موضَّح بالسهم، ويمثل طول السهم مثلًا شدة الضوء. توجد عدة أسهم في الصورة، إلا أنّ أيّ سهمٍ يكفي لتمثيل الضوء وشدته. يمكن تمثيل اتجاه الضوء وشدته بشعاع، والذي هو كائن هندسي له خاصيتان هما: الطول والاتجاه. للضوء الصادر من الشمس خاصيتان، هما: السطوع والاتجاه (مع تجاهل معلومات اللون)، ويتناسب طول الشعاع مع سطوع الضوء. يمكن تمثيل الرياح أيضًا بشعاع، فالرياح لها اتجاه وسرعة، إذ تنتقل ذرة من الغبار مع اتجاه الريح، ويتناسب طول الشعاع مع سرعة ذرة الغبار. ليس للشعاع موضع، إذ تُظهِر الصورة السابقة عدة أسهم تمثل تدفق الضوء القادم من الشمس، ولكن يمكن رسم الأسهم في أيّ مكان طالما أن اتجاهها وطولها هو نفسه. تمثيل الأشعة هل تفترض أن برنامج الرسوميات الحاسوبية يحتاج إلى تمثيل شدة الضوء واتجاهه؟ نعم، في الحقيقة هناك حاجة لذلك. تُستخدَم الأشعة لعدة أغراض في رسوميات الحاسوب ثلاثية الأبعاد، لذلك يجب أن تُمثَّل بطريقة يمكن للبرامج التعامل معها، ويحدث ذلك باستخدام الأرقام. لاحظ أن الصورة التالية تتضمن الآن إطار إحداثياتنا: يُمثَّل الشعاع بمصفوفة عمودية كما هو الحال مع النقاط، ويمكن أن يكون من المربك إلى حدٍ ما أن تُمثَّل النقاط والأشعة باستخدام الشيء نفسه، ولكن ذلك سيثبت أنه هذه الطريقة مناسبة ليتعامل معها الحاسوب. يمكن تمثيل الشعاع بمصفوفة عمودية باتباع الخطوات التالية: اختر إطارًا إحداثيًا. احسب طول X (موجب أو سالب) من ذيل الشعاع إلى رأسه. 3.احسب طول Y (موجب أو سالب) من ذيل الشعاع إلى رأسه. احسب طول Z (موجب أو سالب) من ذيل الشعاع إلى رأسه. ضع هذه الأرقام الثلاثة في عمود. إحدى الطرق الملائمة لذلك هي وضع ذيل الشعاع عند نقطة الأصل، ثم قراءة قيم x و y و z عند رأسه. الأشعة والإطارات كم مترًا في الاتجاه X للمسافة بين رأس الأسهم عن ذيلها في الصورة؟ يمكن أن نخمنها بمقدار حوالي 0.9 متر (3 أقدام). كم مترًا في الاتجاه Y يبعد الرأس عن الذيل؟ يمكن أن نخمنها بمقدار 1.2- متر (‎-4 أقدام). كم مترًا في الاتجاه Z يبعد الرأس من الذيل؟ يمكن أن نخمنها بمقدار 0.9- متر (‎-3 أقدام). إذًا، الشعاع الذي يعطي شدة واتجاه ضوء الشمس في الصورة هو: تمثل المصفوفة العمودية السابقة الشعاع باستخدام إطار الإحداثيات الذي اخترناه، ولكنها ليست الشعاع نفسه. إذا اخترنا إطارًا إحداثيًا مختلفًا، فسيكون الشعاع في المشهد الحقيقي هو نفسه، ولكن سيتغير تمثيله باستخدام الإطار الجديد، وسنواصل في المقال التالي هذه المناقشة. مراجعة سريعة: للنقطة خاصية واحدة فقط هي: الموقع. للشعاع خاصيتان، هما: الطول والاتجاه ولكن ليس له موقع. ترجمة -وبتصرُّف- للفصل Points and Lines من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell. اقرأ أيضًا تعرف على أشهر برامج وتطبيقات تصميم الصور والرسوميات قواعد تصميم الرسوم البيانية قواعد التعامل مع الصور والرسوميات