لوحة المتصدرين
المحتوى الأكثر حصولًا على سمعة جيدة
المحتوى الأعلى تقييمًا في 10/02/22 في كل الموقع
-
وبالمناسبة في visual studio code ال حجم الخط ال front size صغير كيف ازود حجم الخط.2 نقاط
-
اذا انا كاتب كود مكون من خمس اسطر مثلا وبدي اعمل سلاش // للكود كامل هل يوجد اختصار؟2 نقاط
-
سلام عليكم اواجه هذا الخطأ فقط في ال live لكن على الللوكال سيرفر الدنيا شغاله جدا PHP Fatal error: Uncaught Error: Call to a member function bind_param() on bool الكود $name = mysqli_real_escape_string($conn,$_POST['name']); $defaultLang = mysqli_real_escape_string($conn,$_POST['defaultLang']); $section = mysqli_real_escape_string($conn,$_POST['section']); $workTitle = mysqli_real_escape_string($conn,$_POST['workTitle']); $hiring = mysqli_real_escape_string($conn,$_POST['hiring']); $permission = mysqli_real_escape_string($conn,$_POST['permission']); $username = mysqli_real_escape_string($conn,$_POST['username']); $password = mysqli_real_escape_string($conn,password_hash($_POST['password'], PASSWORD_DEFAULT)); $email = mysqli_real_escape_string($conn,$_POST['email']); $created_by = mysqli_real_escape_string($conn,$_POST['created_by']); $created_at = mysqli_real_escape_string($conn,date('Y-d-m')); if (isset($_FILES['image']['name'])) { $filename = $_FILES['image']['name']; // Valid extension $valid_ext = array('png','jpeg','jpg'); $image = time() . $_FILES['image']['name']; // Location $location = '../assets/images/' . $image; // file extension $file_extension = pathinfo($location, PATHINFO_EXTENSION); $file_extension = strtolower($file_extension); // Check extension if(in_array($file_extension,$valid_ext)){ // Compress Image compressImage($_FILES['image']['tmp_name'],$location,35); $imageAdds = $image; } else { exit ; } } else{ $imageAdds = 'bee.png'; } if (mysqli_num_rows($chkUSR) > 0){ echo 'userFound'; exit; } if (mysqli_num_rows($chkMAIL) > 0){ echo 'emailFound'; exit; } $stmt = $conn->prepare( "INSERT INTO users(first_name,lang, section, title, hiring, permission, profile_image, username, password, email,created_at,verified_at,created_by) VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?) "); echo $conn->error; $stmt->bind_param("sssssssssssss", $name,$defaultLang,$section,$workTitle,$hiring,$permission,$imageAdds,$username,$password,$email,$created_at,$created_at,$created_by); //---- //$result = $conn->query("INSERT INTO users(first_name,lang, section, title, hiring, permission, profile_image, username, password, email,created_at,verified_at,created_by) VALUES ('$name','$defaultLang','$section','$workTitle','$hiring','$permission','$imageAdds','$username','$password','$email','$created_at','$created_at','$created_by')"); if ($stmt->execute()) { echo "done"; } else{ echo "Errormessage: %s\n". $conn->error; } الخطأ يشير الى هذا السطر $stmt->bind_param("sssssssssssss", $name,$defaultLang,$section,$workTitle,$hiring,$permission,$imageAdds,$username,$password,$email,$created_at,$created_at,$created_by); ما المشكلة فضلا1 نقطة
-
نعيش حرفيًا في عالم من البيانات، فما نقرؤه وما نكتبه وما نفكر به أنواع من البيانات، وما تستند عليه أفعالنا اليومية وسلوكنا هي أنواع من البيانات. قد تقرر الذهاب إلى التسوق لأنك تحتاج إلى بعض الحاجيات التي سجلتها على قائمتك، إن ما سجّلته على قائمتك هي بيانات، ثم تمضي في طريقك لتقف عند إشارة مرور حمراء، إن وقوفك عند الإشارة الحمراء عائد إلى بيانات أيضًا، فالأحمر للوقوف والأخضر للمتابعة، ثم تصل بعد ذلك إلى المتجر لتتفقد ما تحتاج إليه، فقد تنظر إلى العلامة التجارية للمنتج وهذه بيانات قد تعطيك فكرة عن جودة المنتج، وقد تنظر إلى سعر المنتج وهذه أيضًا بيانات تستخدمها لاتخاذ قرار الشراء وفقًا لميزانيتك، وإن كان المنتج غذائيًا مثلًا ستهتم بتاريخ الإنتاج وتاريخ انتهاء الصلاحية والمكوّنات، فهي بيانات ستؤثر على صحتك، وأخيرًا عندما تنتهي من التسوق وتتوجه إلى كوة المحاسبة سيقرأ الماسح الضوئي رمز المنتج وهو نمط من البيانات التي تعرّف هذا المنتج وتحدد هويته وقد خُزّنت ضمن هذا الرمز وفق سلسلة من الأرقام أو الأحرف أو كليهما كما خزّنت على حاسوب كوة المحاسبة أيضًا بطريقة ما. ما هي البيانات إذًا وما هي أنواع البيانات؟ من أين تأتي البيانات؟ كيف نستقبلها وكيف نفهمها؟ كيف نصنّف أنواع البيانات المختلفة وأين نخزّنها وكيف نسترجعها ونحللها؟ وكيف نستفيد منها في المحصلة؟ سنحاول في هذا المقال الإجابة عن الأسئلة السابقة بشيء من التفصيل لتكون عونًا لك في تعاملك مع أنواع البيانات سواء كنت راغبًا في أن تكون مصممًا لقواعد البيانات أو محللًا لأنواع البيانات أو مبرمجًا لها. إليك فهرس بعناوين المقال لتسهيل الوصول إلى مختلف أجزاء المقال: تعريف البيانات الفرق بين البيانات والمعلومات من أين تأتي البيانات؟ أنواع تخزين البيانات تصنيف أنواع البيانات Data Types البيانات الكمية البيانات النوعية البيانات المنطقية أنواع البيانات في الحاسب تصنيفات البيانات الرقمية أنواع البيانات في لغات البرمجة أنواع البيانات المستخدمة في قواعد البيانات خاتمة تعريف البيانات البيانات Data تُعرَّف بأنها مقادير منفصلة على شكل رموز أو إشارات قابلة للتحليل والمعالجة، ويمكن للبيانات أن تكون واضحةً ومفهومة لنا دون سياق محدد -أي دون أي تسلسل أو ترابط- مثل مجموعة أرقام تمثل أحجية، فالأرقام مقاديرٌ مفهومةٌ بالنسبة لنا، لكن الربط بينها لحل الأحجية قد يكون عصيًا. وقد لا تكون البيانات مفهومةً كخطوط رمز الماسح الضوئي (بار كود). تُدعى النتيجة المستخلصة من تحليل مجموعة من البيانات والربط بينها بالمعلومة أو المعلومات عمومًا information، كما تُدعى أصغر وحدة من مجموعة بيانات يمكن أن تُستخدم أو تفهم باستقلالية بعنصر البيانات datum. عندما نجمع المعلومات المتعلقة بموضوع معين وننظمها ثم نفهمها من خلال التطبيق والممارسة، سيكون توثيق هذه المعلومات المصنّعة انطلاقًا من البيانات معرفةً knowledge، أما الأسلوب الأمثل في تطبيق هذه المعرفة فقد ندعوه حكمة wisdom. إذًا فالبيانات عمومًا هي وسيلة للحصول على معلومات أو وسيلة لتمثيلها بطريقة أفضل كي تُعالح وتُستخدم. وقد تكون هذه البيانات مجرّدة كأسماء علامات تجارية وقد تكون مقاسة كدرجات الحرارة أو نسبة الفائدة أو عدد الولادات خلال عام. تُنظم البيانات ضمن بنىً خاصة تسمى بنى البيانات أو هياكل البيانات data structure لتسهيل الوصول إليها واستخلاص المعلومات منها مثل الجداول، وقد جُمعت أنواع البيانات ما قبل الثورة الرقمية في مراجع وكتب ووثائق، لكن مع بزوغ فجر الحوسبة كان الانتقال إلى البيانات الرقمية أمرًا حتميًا لتقود بالفعل العالم الرقمي منتجات ومختصين نحو تقنيات أكثر قدرة وترابطًا ابتداءً بقواعد البيانات النمطية databases إلى تقنيات التعامل مع البيانات الضخمة Big data وصولًا إلى تطوير الذكاء الصنعي AI. الفرق بين البيانات والمعلومات يجري الخلط في مواضع عدة بين البيانات والمعلومات على أنها الشيء ذاته وهذا أمر خطأ، فهناك فرق بيّن بين المصطلحين تعريفًا وغاية، ولقد أشرنا سابقًا أن البيانات تعرّف حقائق مفردة، بينما تمثل المعلومات تنظيمًا لهذه الحقائق أو تفسيرًا لها. تأتي البيانات بأشكال مختلفة، نصوصًا وأرقام وأشكال وصور وتواريخ لكنها لا تحمل دلالات على أهميتها أو الحاجة لوجودها، فقد يشير جهاز قياس تردد الصوت إلى القيمة 12 كيلو هرتز عندما يعجز المريض عن سماع أي صوت في عيادة تخطيط السمع، إذ القراءة بحد ذاتها لا دلالة لها ولن يتمكن سوى المختص من تأويلها إلى المعلومة التالية "المريض يعاني نقصًا في السمع". وقد تجد أيضًا أن مقدار المبيعات من منتج ما هو 20 جهازًا في العام، لن يقدم كذلك عنصر البيانات هذا أي دلالة ما لم يحلل ويوازن ويتحول إلى معلومة مثل "حققت الشركة هذا العام نسبة مبيعات عالية!". وهكذا يمكن أن نلخص الفرق بين البيانات والمعلومات كالتالي: البيانات مجموعة من الحقائق غير المنظمة، أما المعلومات فهي من يضع تلك البيانات في سياقها الصحيح. البيانات مصدر خام للحقائق دون أية دلالات وقد لا تتمكن من قراءتها أحيانًا، أما المعلومات فهي التي توضّح أنواع البيانات وتستخلص منها ما يُفهم ويُطبق ويُختبر. البيانات حقائق مستقلة بذاتها وقد لا تربط بينها أية علاقات، بينما تجد المعلومات العلاقات التي تربط بين أنواع البيانات لعرض صورة أوسع عن الظاهرة المدروسة. لا تعتمد البيانات على المعلومات لكن العكس صحيح. لا يمكن الاعتماد على البيانات لاتخاذ القرارات، فلا بد من وجود معلومات حتى يُتّخذ القرار الصحيح. من أين تأتي البيانات؟ تأتي البيانات -والتي تتنوع إلى أنواع البيانات- من تطور الفهم البشري للبيئة المحيطة به، وبالتالي من تطور معارفه والحاجة إلى توثيق هذه المعارف ووضعها حيز التنفيذ بالأسلوب الأمثل والأكثر كفاءة من جميع النواحي تحليلًا ومعالجة وسرعة، لكن يمكننا القول أن الأساليب الأساسية التي نحوز بها على بيانات أو نحدّث الموجودة منها قد تنحصر بما يلي: الافتراض assumption المراقبة observations القياس measurement التحليل analysis الافتراض assumption عادة ما يكون الافتراض منهجيًا، أي يستند إلى أفكار مسبقة عن موضوع ما أو إلى معلومات غير دقيقة أو بياناتها غير كافية. عادة ما تكون أنواع البيانات المفترضة خطوة مرحلية تُلغى لاحقًا عند حيازة البيانات المطلوبة، إلا أن توثيقها ضروري جدًا. فلو أردنا مثلًا أن نقدّر عدد المشترين المتوقعين لمنتج جديد في مدينة ما لدراسة جدوى توزيعه فيها سيكون هذا الرقم مفترضًا والنتائج التي تتأتى عنه افتراضيةً أيضًا ستصحح مع الوقت لكن بالطبع سيكون عدد المشترين متوقعًا بناء على أفكار أو دراسات مشابهة. المراقبة observations وهي إحدى الطرق الإحصائية Statistics المتبعة في حيازة البيانات، إذ تجري مراقبة ظاهرة اجتماعية أو اقتصادية أو غيرها ضمن جماعة population محددة للحصول على أنواع بيانات محددة تتعلق بالحالة المدروسة، كأن نسجل بيانات عن عدد المتزوجين تحت سن الثلاثين في منطقة معينة مثل سن الزواج وتاريخه وعدد الأطفال. تقدم هذه البيانات قاعدة قوية للحصول على الكثير من المعلومات التي يحتاجها الإحصائي للإجابة عن الأسئلة التي صمم هذه الدراسة لأجلها. القياس measurement تُعنى هذه الطريقة بالحصول على بيانات كمية (سنتحدث عنها لاحقًا) ثابتة توصّف الحالة المدروسة، ويقصد بالحصول على قيمة: إجراء ما يلزم من الاختبارات لتحديد القيمة المقاسة بأقل خطأ ممكن. من الأمثلة على البيانات المحازة عن طريق القياسات درجات الحرارة في مدينة محددة أو منسوب المياه في نهر خلال العام أو كمية المشتريات من منتج محدد وغيرها. التحليل analysis تهدف هذه العملية إلى تفكيك ظاهرة مجهولة أو مجموعة معلومات مجهولة التكوين إلى بياناتها الأولية لفهمها والاستفادة منها كالبيانات الناتجة عن تحليل الطيف الضوئي لنجم بعيد أو تحليل إشارة لاسلكية مركبة إلى مكوناتها الأساسية للحصول على بيانات تتعلق بالتردد والشدة. إذًا فعمليات الحصول على أنواع البيانات أو حيازتها تتعلق بالظاهرة المدروسة والهدف النهائي من هذه الدراسة والمعلومات التي يجب الحصول عليها أو فهمها تمهيدًا لتخزينها أو وضعها حيز التطبيق. أنواع تخزين البيانات تخزن البيانات في وسائط تخزين والتي إما أن تكون فيزيائية باستعمال الأوراق والدفاتر وكل ما يصلح للكتابة عليه أو باستعمال وسائط تخزين رقمية عبر الحواسيب التي هي الأشيع حاليًا بما أنها تسهل عمليات البحث والفهرسة ومعالجة البيانات. فبالنسبة لتخزين البيانات في الحواسيب، فإنها تعتمد على وسائط تخزين رقمية مثل الأقراص المدمجة والأقراص الصلبة HDD وذواكر الحالة الصلبة SSD والتي تتطور تدريجيًا مع الزمن وفيها إما أن تخزن البيانات مباشرةً باستعمال نظام ملفات يوفره نظام التشغيل أو تخزن بطريقة مهيكلة عبر جداول مثلًا لتسهيل معالجتها والوصول إليها وهنا يمكن استعمال برامج بسيطة مثل برنامج إكسل من مايكروسوفت أوفيس وقواعد بيانات أكسس وحتى استعمال قواعد بيانات مخصصة تكون عادة الأساس الذي ترتكز عليه تطبيقات الحاسوب كلها. تصنيف أنواع البيانات Data Types أنواع البيانات Data Types تُصنّف ضمن ثلاثة فئات رئيسية هي: البيانات الكمية quantitative data البيانات النوعية qualitative data البيانات المنطقية logical data وسنشرح كل تصنيف منها. البيانات الكمية البيانات الكمية هي البيانات التي تأخذ قيمًا عددية أو ناتجة عن الموازنة مع مقاييس عددية ومن الأمثلة عليها ارتفاع بناء، فلا بد من أن يكون قيمة عددية محددة 30 متر مثلًا، أو أن تحدد مستوى مهارتك في لغة برمجة معينة على مقياس من 1 إلى 10. تنتج هذه البيانات عن طريق قياس المقادير عبر الأجهزة المختلفة كمقاييس الضغط والحرارة والارتفاع، وقد نحصل عليها من الاستبيانات questionnaire التي تُنشر وتتطلب الإجابة عنها عن طريقة التقييم العددي لأسئلتها. قد نجد أيضًا تصنيفات فرعية لهذا النوع من البيانات: بيانات منفصلة discrete data: وهي بيانات كمية تأخذ قيمها من مجموعة قيم محددة سلفًا كعدد الوجبات التي يمكن للمطاعم أن تقدمها أو عدد الأولاد في عائلة محددة. بيانات مستمرة continuous data: وتمثل عادة القيم التي تقيسها التجهيزات والتي يمكن أن تأخذ أي قيمة عددية ضمن مجال محدد مثل درجات الحرارة، ويمكن تصنيف هذه الأخيرة إلى: بيانات مجالية interval data: وهي بيانات تمثل قيم عددية مرتبة تزيد كل قيمة عن التي تسبقها بمقدار محدد تمامًا كأن نعرض تسلسل طلبات الشراء، أو أن نسجل ارتفاع بالون في الجو كلما ارتفع 10 أمتار عن سطح البحر. بيانات نسبية Ratio data: وهي بيانات مستمرة تمثل نسبة تكرار حالة إلى جميع الحالات الممكنة كأن تحدد احتمال إصابة هدف أو إمكانية ولادة طفل مصاب بمرض وراثي. بيانات إحصائية: وهي البيانات التي تنتج عن تطبيق العلاقات الرياضية الخاصة بالإحصاء ومن أنواع البيانات الإحصائية: المتوسط الحسابي mean: ويقيس مجموع عدة قراءات إلى عددها كأن نحسب المتوسط الحسابي لأطوال الذكور في بيئة معينة بجمع أطوال جميع الذكور المشاركين في الدراسة ثم تقسيم الناتج على عددهم. المتوسط الهندسي geometric mean: وهو الجذر من المرتبة n لجداء القراءات المتعلقة بظاهرة معينة. الوسيط median: ويحدد القيمة التي تأتي في وسط مجموعة قيم مرتبة أي بمعنى آخر القيمة التي تقسم مجموعة قيمة مرتبة إلى مجموعتين متساويتين. الانحراف المعياري standard deviation: ويمثل مقدار ابتعاد عينة عن المتوسط الحسابي. المدى range: الفرق بين أعلى وأدنى قراءة من مجموعة قراءات. المنوال mode: ويحدد القيمة أو القيم الأكثر ورودًا. البيانات النوعية البيانات النوعية هي البيانات التي تصف نوعية أو خصائص الظاهرة المدروسة وبالتالي هي غير قابلة للعد وصعبة القياس والتحليل الدقيق، كأن تكون ملاحظات مأخوذة عن نوعية الوجبات المقدمة في مطعم أو أسماء الناجحين في اختبار. قد تكون هذه البيانات على شكل كلمات تصف الظاهرة ولا تحتاج إلى تحليل أبعد أو يمكن أن تكون لهذه البيانات أنماط محددة أو معانٍ محددة لا بدّ من تحليلها للحصول على المعلومات المطلوبة مثل سمات السلوك العدواني لعينة من المرضى النفسيين أو الميزات الأنسب لأحد المرشحين للحصول على وظيفة معينة. كما قد تكتب البيانات النوعية على شكل بيانات رقمية لكنها لا تحتمل معنى الأعداد الرياضي ولا توازن بأعداد لا تماثلها كأن نجعل الرقم 1 يدل على جنس المولود إن كان أنثى و 0 إذا كان ذكرًا. وقد نجد أيضًا تصنيفات فرعية لهذا النوع من أنواع البيانات مثل: بيانات فئوية categorical data: وهي بيانات تمثل ميزة محددة للعينة المدروسة مثل العمر، والجنس، واللغة. بيانات مسماة nominal data: وهي بيانات نوعية تأخذ قيمها ضمن مجموعة محددة من الخيارات كأن تختار لغة من بين خمس لغات محددة سلفًا أو أن تختار تقييمًا لخدمة زبائن من بين عدة تقييمات متاحة. بيانات مرتبة ordinal data: وهي ببساطة بيانات مسماة لكنها مرتبة على أساس محدد كأن تحدد البيانات قائمة العقوبات التدريجية التي تطبق على مخالفي النظام الداخلي لمؤسسة او شركة أو تسلسل خطوات إصلاح خلل في برنامج. ما الفرق بين البيانات الكمية والنوعية؟ شرحنا ما هي البيانات الكمية والنوعية ويجدر الذكر أنه يمكن لعينة بيانات نفسها أن تنقسم إلى بيانات كمية ونوعية في الوقت نفسه مثل عينة بيانات من مجموعة مدارس، فقد تنقسم إلى بيانات كمية من عدد الطلاب وقد تنقسم إلى بيانات نوعية بناءً على جنس الطلاب بين ذكر وأنثى وهكذا لذا وجب التفريق جيدًا بين البيانات الكمية والنوعية. أمر آخر وهو أن العمليات المطبقة على البيانات الكمية قد تختلف أغلب الأحيان عن تلك المطبقة على البيانات النوعية فقد يصلح تطبيق عمليات إحصائية وعمليات رياضية على بيانات كمية في وقت لا يصلح تطبيقها على بيانات نوعية بما أن قيمة البيانات الكمية تمثَّل مباشرةً بعدد، وهذا خلاف البيانات النوعية فحتى لو مثلناها بعدد مثل تمثيل الطلاب الذكور بعدد 1 والطلاب الإناث بعدد 2 فهو طريقة لعرض البيانات بشكل آخر. البيانات المنطقية وهي أبسط أنواع البيانات، وتجيب عن سؤال ما بصحيح أو خاطئ، نعم أو لا وقد تأخذ إحدى القيمتين الرقميتين 0 أو 1، وتدعى أيضًا البيانات البوليانية نسبة إلى الجبر البولياني. قد تصنف هذه البيانات على أنها بيانات نوعيّة إذا جاءت على شكل "صحيح/خاطئ" أو "نعم/لا"، وقد تصنّف أنها بيانات كمية إن جاءت على شكل "0/1". أنواع البيانات في الحاسب عزز ظهور الحواسب قدرة البشر على حيازة وتخزين كميات هائلة من البيانات وأمنت الوسائل اللازمة لتحليلها واستخلاص المعلومات عنها والاستفادة من تلك المعلومات في عمليات اتخاذ القرار، ولا تختلف أنواع البيانات في الحاسب وفي العالم الرقمي من حيث التعريف والغاية لكنها تخزّن وتعالج بطريقة أفضل وأسرع، لهذا السبب وضعت بعض التصنيفات الفرعية وحددت أنواع للبيانات تلائم طريقة عمل الحواسيب. تمثّل البيانات في الحواسيب على شكل سلاسل من الواحدات والأصفار وهي ما يفهمه الحاسوب أولًا وآخرًا ويُدعى أصغر حجم لتخزين عنصر البيانات "بت Bit" ويخزن القيمة 0 أو 1 ومن البت يتكون البايت Byte الذي هو 8 بت والكيلو بايت والميغا بايت …إلخ. تصنيفات البيانات الرقمية تُدعى أنواع البيانات التي تُخزّن على شكل سلاسل من الأصفار والواحدات وتعالج وفق هذه الطريقة بالبيانات الرقمية digital data، وقد نجد أن البيانات الرقمية قد تأخذ أصنافًا جديدة منها: بيانات مهيكلة structured: تُرتب البيانات المهيكلة وفق نموذج بيانات محدد لتسهل معالجتها وتخزينها والوصول إليها مثل الجداول المكوّنة من أسطر وأعمدة والتي تُعد أساس قواعد البيانات العلاقيّة relational databases أو على شكل بنية هرمية متداخلة hierarchical data structure أو أنها قادرة على تخزين كائنات objects لها هيكليات محددة سلفًا. بيانات غير مهيكلة not structured: البيانات غير المهيكلة هي تلك التي تُنظّم فيها البيانات بطريقة محددة كأن توضع في ملفات نصية أو تُستخدم بعض اللغات التوصيفية في تنظيمها. بيانات وصفية metadata: وهي بيانات نصية تصف بيانات أخرى كأن تحدد إصدار برنامج وتاريخ الإصدار ومعلومات عن ترخيص الاستخدام وهكذا. بيانات خام raw Data: وهي تسلسل غير منسّق من الواحدات والأصفار يُخزّن للمعالجة اللاحقة. القواميس dictionary: وهي نوع من أنواع البيانات التي يمكن الوصول إليها بطريقة "مفتاح-قيمة" أي تُفهرس فيها بيانات "القيمة" وفقًا لبيانات "المفتاح" وللوصول إلى القيمة قراءةً أو تخزينًا لا بد من معرفة المفتاح المرتبط بها. البيانات الضخمة big data: ظهر هذا المصطلح في فترة قريبة نسبيًا ليدل على أنواع البيانات التي تتجاوز أحجامها البيتا بايت (1000 تيرا بايت)، وبالتالي سيصعب معالجة هذا الكم الهائل من البيانات من قبل حاسوب واحد أو تنظيمها باستخدام قواعد البيانات النمطية، لهذا توزّع المهام على عدة حواسب رئيسية تتمتع بقدرات كبيرة في المعالجة من خلال استخدام خوارزميات واختبارات متقدمة بغية استخلاص المعلومات والرؤى التي تقدمها تلك البيانات خلال فترة زمنية مقبولة. أنواع البيانات في لغات البرمجة تختلف أنواع البيانات التي تستخدمها لغات البرمجة للتعبير عن القيم التي تتعامل معها وفقًا للغة البرمجة نفسها فكل لغة برمجة لها مجموعة أنواع بيانات محددة تتعامل معها توضحها في توثيقها الرسمي فانظر مثلًا مقال أنواع البيانات في لغة بايثون في أكاديمية حسوب وقسم أنواع البيانات في لغة بايثون في توثيق موسوعة حسوب وكذلك صفحة أنواع البيانات في لغة PHP وصفحة أنواع البيانات الأساسية في لغة TypeScript وصفحة أنواع البيانات الأساسية في لغة كوتلن وغيرها، فكل لغة كما أشرنا تملك أنواع بيانات تحددها صراحة لما يترتب عليها لاحقًا من ضبط العمليات التي يمكن تنفيذها على كل نوع بيانات، فمثلًا الأعداد تطبق عليها عمليات رياضية من جمع وطرح وضرب والنصوص تطبق عليها عمليات القص والجمع مع نصوص أخرى والتنسيق وغيرها. دورة تطوير التطبيقات باستخدام لغة Python احترف تطوير التطبيقات مع أكاديمية حسوب والتحق بسوق العمل فور انتهائك من الدورة اشترك الآن وتنقسم لغات البرمجة في طريقة تحديد أنواع البيانات إلى قسمين إما بتحديدها صراحةً أثناء كتابة الشيفرة وتدعى آنذاك لغات برمجة صارمة في تحديد الأنواع Strongly typed language أو بترك الأمر للغة البرمجة لتحديدها أثناء تنفيذ الشيفرة وتدعى آنذاك لغات برمجة متهاونة في تحديد الأنواع Loosely typed language. أما في لغات البرمجة التي تعد صارمة في تحديد الأنواع مثل لغة سي C وجافا Java، فهي تفرض على المبرمج تحديد نوع المتغير عند تعريفه أول مرة ويبقى هذا النوع ملازمًا له طيلة عمل البرنامج ولا يمكن تغييره مطلقًا ولا يمكن استعماله إلا في العمليات المرتبطة بنوعه المحدد وغيرها من القواعد الأخرى التي تختلف باختلاف اللغة، فالمثال التالي من لغة سي يعرِّف ثلاثة متغيرات الأول عدد صحيح والثاني عدد عشري والثالث محرف واحد: int intNumber = 2; float floatNumber = 2.3; char character = 'e'; وإن لم يتبع المبرمج هذه القواعد فسيحصل على خطأ قبل تنفيذ الشيفرة وقت تصريفها (إن كانت اللغة مصرَّفة compiled مثلًا)، فستحصل على خطأ إن جربت جمع العدد الصحيح intNumber السابق مع الحرف character بالشكل intNumber + character مباشرةً وكذلك إن أردنا جمعه مع العدد العشري floatNumber وهنا يجب إجراء عملية تحويل صريحة للنوع انظر مثلًا: int intNumber = 2; float floatNumber = 2.3; int sum = intNumber + (int)floatNumber; printf("Value of sum : %d\n",sum); عندما جمعنا العدد الصحيح intNumber مع العدد العشري floatNumber حولنا الأخير إلى عدد صحيح عبر تحديد النوع بين القوسين قبل المتغير ثم جمعنا العدد لنحصل على الناتج التالي: Value of sum : 4 ولاحظ أن الفاصلة العشري قد أُهملَت بما فيها من أجزاء عشرية وهذا ناتج عملية التحويل. تختلف لغات البرمجة أيضًا من ناحية التصريح والتلميح في عمليات التحويل بين الأنواع casting ففي التصريح يضطر المبرمج إلى ذكر النوع المراد التحويل إليه صراحةً وسيحصل على خطأ إن لم يفعل، وفي التلميح تكون اللغات ذكية في استنتاج النوع المراد التحويل إليه وتدعى smart casting فمثلًا إن جربت ما يلي في لغة سي: int intNumber = 2; float floatNumber = 2.3; int sum = intNumber + floatNumber; printf("Value of sum : %d\n",sum); فستحصل على الناتج 4 كعدد صحيح لأن لغة سي مباشرةً حولت العدد العشري إلى صحيح بما أن المتغير الذي سنخزن فيه النتيجة من نوع عدد صحيح وكذلك العدد الأول عدد صحيح، أما إن جربنا ما يلي: int intNumber = 2; float floatNumber = 2.3; float sum = intNumber + floatNumber; printf("Value of sum : %f\n",sum); فستحصل على ناتج 4.3 حتى لو كان العدد الأول صحيح إلا أن المتغير المراد تخزين القيمة فيه اختلف نوعه فاختلفت عملية التحويل الآلية وجرى تحويل العدد الصحيح إلى عدد عشري. وأما في لغات البرمجة التي تعد متهاونة في تحديد النوع مثل جافاسكربت وبايثون ولغة PHP فلا حاجة لتحديد أنواع البيانات للمتغيرات ويكتفي المبرمج بالتصريح عن المتغير فقط دون نوعه، فانظر إلى المثال التالي في لغة جافاسكربت الذي يعرف المتغيرات الثلاثة كما في المثال السابق: let intNumber = 2; let floatNumber = 2.3; let character = 'e'; سيُترك الأمر إلى لغة البرمجة لتحديد نوع المتغير أثناء وقت تنفيذ الشيفرة runtime لتحديد العمليات التي يمكن تنفيذها مع كل متغير وفق نوع، ولاحظ أنه يمكن لمتغير أخذ نوع عدد صحيح أن يأخذ نوع آخر مثل عدد عشري أو نص ولا يُعد ذلك خطأ: let intNumber = 2; intNumber = 'e'; وأما بخصوص عمليات التحويل بين الأنواع فهو أمر متروك كليًا إلى لغة البرمجة وذكائها، فإن جربنا الجمع بين العدد الصحيح والعشري كما فعلنا مع لغة سي الصارمة في تحديد الأنواع: let intNumber = 2; let floatNumber = 2.3; let sum = intNumber + floatNumber; console.log('Value of sum: ' + sum) فسنحصل على النتيجة التالية: Value of sum: 4.3 لاحظ أن عملية التحويل مالت إلى كفة العدد العشري ولاحظ أيضًا أننا جمعنا نصًا 'Value of sum: ' مع عدد sum أثناء طباعة النتيجة وكان الناتج نصًا ولم نحصل على خطأ بل اجتهدت لغة جافاسكربت في عملية التحويل ما يمكنها قبل أن تطلق أي خطأ للمبرمج، وقد شاعت الكثير من الدعابات بين المبرمجين حول عثرات لغة جافاسكربت تحديدًا في ضبط عملية التحويل بين أنواع البيانات بدقة. وهذا الأمر يربك المبرمجين بعض الأحيان في اللغات المتهاونة في تحديد النوع لعدم معرفة نوع البيانات النهائي للعملية بالضبط، فتخيل مثلًا في تطبيق بنكي مبني بلغة متهاونة في ضبط النوع أو أن الأمر متروك للغة البرمجة لاستنتاج نوع البيانات أثناء وقت التنفيذ فيرسل مستخدمًا مبلغ 100.54 دولار لصديقه ليستلم الأخير مبلغ 100 فقط ويُعلل الأمر بأن لغة البرمجة قد أخطأت في عملية تحويل نوع البيانات لذا اختيار طريقة التعامل مع البيانات أمر مهم جدًا يعتمد على نوع التطبيق المراد العمل عليه! في النهاية، المتغيرات في لغات البرمجة هي حاويات للبيانات التي تصنف إلى أنواع وقد تُحدد أحجام تلك الحاويات وفقًا لحجم البيانات المخزنة فيها تلقائيًا كما في اللغات المتهاونة في تحديد النوع أو وفقًا لنوع البيانات المحدد لها ويحصل خطأ إن تجاوزت البيانات الحجم المضبوط بنوع البيانات ذاك كما في اللغات الصارمة في تحديد النوع فمثلًا يأخذ متغير بنوع بيانات short حجم 2 بايت من الذاكرة لتخزين أعداد تتراوح بين القيمة -32768 والقيمة 32767 فقط بينما يأخذ متغير من النوع bool حجم 1 بت فقط في لغة سي. وأيًا كانت أنواع البيانات التي تُعرّفها لغات البرمجة المختلفة إلا أنها تشترك جميعها بأنواع بيانات عامة سنتحدث عنها بالتفصيل. الأعداد الصحيحة تعبّر الأعداد الصحيحة Integer عن البيانات بالأعداد الكاملة أي دون فواصل عشرية سواء كانت الأعداد موجبة أو سالبة مثل 5، 110-، 42345، وهكذا، وتُستخدم الأعداد الصحيحة لتمثيل مقادير مثل عدد الولادات في عام أو عدد مرات وقوع حدث معين أو الأرقام التسلسلية لمنتجات أو رقم جواز السفر وما شابه. تمثل لغات البرمجة الأعداد الصحيحة ببايت واحد أو 2 بايت أو 4 بايتات، ويعود السبب في ذلك إلى حجم البيانات التي تريد تمثيله فإن أردت أن تمثل أعدادًا صحيحة من 0 إلى 100 مثلًا لا حاجة عندها لأربعة بايتات ويُكتفى ببايت واحد، أما إن احتجت إلى تخزين أرقام ضخمة ككتلة الأرض مثلًا فستحتاج إلى عدد صحيح من أربع بتات بالتأكيد. إليك بعض الأمثلة: في اللغة C++/C: // متغير حجمه أربعة بايتات ويخزّن فيه بيانات عددية صحيحة سالبة وموجبة int a =0; // متغير حجمه بايت واحد ويخزّن فيه بيانات عددية صحيحة موجبة وسالبة int8_t a=0; // متغير حجمه بايتين ويخزّن فيه بيانات عددية صحيحة موجبة وسالبة int16_t a=0; // متغير حجمه بايت واحد ويخزّن فيه بيانات صحيحة موجبة فقط uint8_t a=0; في اللغة Java: // متغير حجمه بايت واحد ويخزّن فيه بيانات عددية صحيحة موجبة وسالبة byte x=0; // متغير حجمه بايتين ويخزّن فيه بيانات عددية صحيحة موجبة وسالبة short x=0; // متغير حجمه أربعة بايتات ويخزّن فيه بيانات عددية صحيحة موجبة وسالبة int a=0; إذًا تختلف طريقة تمثيل الأعداد الصحيحة وفقًا للحجم المحجوز من الذاكرة من لغة إلى أخرى ويمكنك العودة إلى ويكيبيديا لتتعرف على طريقة تمثيل البيانات الصحيحة في أكثر اللغات انتشارًا. الأعداد الحقيقية تمثل الأعداد الحقيقية Real numbers جميع الأعداد الصحيحة والعشرية ذات الفاصلة الموجبة منها والسالبة مثل 2.56 أو 2341.234- وهكذا، وتُستخدم هذه الأعداد عند الحاجة إلى تخزين قراءات لمقادير فيزيائية مثل درجات الحرارة أو نواتج العمليات الحسابية المتنوعة كناتج عملية قسمة أو حساب الجذور التربيعية وما شابه. تمثل لغات البرمجة الأعداد الحقيقية بكلمة ذات أربع بايتات 232 عددًا أو كلمة ذات ثمان بايتات 264 عددًا، وتختلف تسمية الأعداد الحقيقية من لغة إلى أخرى. إليك بعض الأمثلة: في اللغات #C++/Java/C: // متغير حجمه أربعة بايتات ويخزّن فيه بيانات عددية حقيقية بإشارة float a=0; // متغير حجمه ثمان بايتات ويخزّن فيه بيانات عددية حقيقية بإشارة double a=0; الاختلاف بين نوع البيانات float ونوع البيانات double هو في دقة الأجزاء العشرية أي الأرقام المخزنة بعد الفاصلة العشرية، فالثاني هو عدد عشري مضاعف الدقة عن الأول. البيانات المنطقية البوليانية تمثل هذه البيانات إحدى القيمتين 0 أو 1 وتحجز بتًا واحدًا من الذاكرة، تُستخدم هذه البيانات لتخزين البيانات الناتجة عن أسئلة تحتمل فقط جوابًا بنعم/لا أو صح/خطأ، كأن تكون غرفة في فندق ما محجوزة أو هل اشترى عميل منتج معين أم لا وهكذا. إليك بعض الأمثلة: في لغة JAVA: // متغير حجمه بت واحد ويخزّن فيه قيمة منطقية 0 أو 1 boolean a=1; في لغة ++C: // متغير حجمه بت واحد ويخزّن فيه قيمة منطقية 0 أو 1 bool a=0; المحارف والنصوص تُمثّل هذه البيانات محرفًا واحدًا character كحرفٍ "ب" مثلًا أو رمزٍ "#" مثلًا أو علامة ترقيمٍ ":" مثلًا أو بعض المحارف الخاصة (لها استخدامات خاصة ولا تطبع على الشاشة كالمحارف التي تهيئ موقع الحركات في اللغة العربية)، وتُمثّل المحارف بكلمة من بايت أو بايتين أو ثلاثة أو أربعة وذلك وفقًا لطريقة الترميز. فترميز ASCII مؤلف من 128 أو 256 محرفًا أي يستخدم بايت واحد وقد وُسِّعت إلى الترميز الموحد UTF-8 الذي يستخدم من بايتين إلى أربعة بايتات ويرمز ملايين المحارف التي تغطي معظم الرموز والحروف في جميع اللغات المعروفة كما ظهرت توسيعات أخرى لمحارف ASCII مثل ISO وOEM وwindows125x وغيرها. تتعامل مختلف لغات البرمجة مع المحارف وتعرفها بطرق مختلفة، وإليك بعض الأمثلة: في لغات ++JAVA/C#/C: // متغير يعبّر عن محرف واحد char ch="#"; هذا بخصوص المحارف ولكن ماذا لو أردنا تخزين نص في متغير؟ النص String هو في الواقع سلسلة متلاحقة من المحارف أو مصفوفة من المحارف array of characters وبالتالي تُشتق الأنواع النصية انطلاقًا من المحارف وتتعامل معها انطلاقًا من العمليات على المحارف أيضًا، وتُعرف معظم اللغات هذا النوع بالاسم string. إليك مثالًا: في لغة ++C: #include <string> //إدراج المكتبة المعيارية الخاصة بالتعامل مع النصوص using std::string // استخدام فضاء أسماء النوع النصي int main(){ string s1= "مرحبًا"; sting s2="أيها العالم"; cout<< s1+s2;// "ستكون النتيجة "مرحبًا أيها العالم return 0; } انتبه إلى أنَّ لغة البرمجة قد تعامل المحرف معاملة النص وتدخله ضمن نوع النص String مثل لغة جافاسكربت وقد تميز اللغة بين المحرف Char وبين النص أو السلسلة النصة String كما في لغة جافا وسي. أنواع البيانات مقابل هياكل البيانات تُدعى الأنواع المدمجة في أي لغة بالأنواع الأساسية basic أو البدائية primitive ويمكنك استخدامها مباشرة في تعريف المتغيرات دون أية مقدمات فلغة جافاسكربت مثلًا التي تتصف بأنها متهاونة في تحديد أنواع البيانات تملك الأنواع الأساسية التالية: String: يمثل النصوص والسلاسل النصية. Boolean: يمثل القيم المنطقية مثل صح/خطأ. Number: يمثل الأعداد. BigInt: يمثل الأعداد الكبيرة جدًا. Undefined: يمثل عدم التعريف. Null: يمثل القيمة الفارغة أو عدم وجود قيمة. Symbol: يمثل الرموز الفريدة الخاصة. Object: يمثل هيكلة لتخزين البيانات. ناقشنا بعض الأنواع السابقة في القسم السابق والتي قلنا أن أغلب لغات البرمجة تشترك فيها ولكن أريد التركيز على النوع الأخير Object فقد تطلق لغة البرمجة على طريقة وهيكلة محددة لتخزين البيانات بنوع بيانات وقد تكون من ضمن الأنواع الأساسية كما رأينا في لغة جافاسكربت التي هي عبارة عن طريقة تخزين بيانات على شكل مفتاح/قيمة key/value مثل: const colorsObj = { black: '#000000', white: '#ffffff', red: '#ff0000', cyan: '#00ffff', pink: '#ffc0cb' } لاحظ أننا ربطنا اسم كل لون بقيمته الست عشرية والتي تمثِّل سلسلة نصية string ويمكننا الوصول إلى قيمة اللون الأسود مثلًا بالشكل colorsObj.black، ويمكن وضع أي نوع بيانات من الأنواع السابقة مكان النص. ومن هذه الهيكلة تُشتق هياكل بيانات أخرى أشهرها على الإطلاق المصفوفات Arrays التي تمثل بالشكل التالي في جافاسكربت: const colorsObj = [ '#000000', '#ffffff', '#ff0000', '#00ffff', '#ffc0cb' ] ستجد الكثير من أشكال هياكل البيانات ولا يسعنا في هذا المقال حصرها كلها ولكن وجبت الإشارة إليه بأنه وسيلة مهمة جدًا لتنظيم البيانات وهيكلتها وقد يعدها البعض نوعًا من أنواع البيانات إلا أنها عبارة عن حاويات تحوي البيانات وتسهل الوصول إليها. أنواع البيانات المستخدمة في قواعد البيانات تحدد معظم قواعد البيانات -وهي برمجيات صممت لاحتواء البيانات وتنظيمها والتعامل معها- أنواع البيانات التي تخزّنها كي يسهل التعامل معها وتعديلها، وتستعمل قواعد البيانات جميع الأنواع التي تستخدمها لغات البرمجة أي: الأعداد الصحيحة integer. الأعداد العشرية (وهي أعداد حقيقية) ذات الفاصلة العائمة float. البيانات المنطقية (0 أو 1). المحارف character. القيم النصية string. ويضاف إليها: المحارف متغيرة الطول varchar: وتمثل مجموعة محددة الطول من المحارف المتتابعة فعندما نحدد نوع أحد البيانات على أنه varchar(20) أي أن العدد الكلي للمحارف في هذا المتغير هو 20 محرفًا. القيم الزمنية والتاريخ date-time: وتخزن بيانات تتعلق بالتاريخ (يوم:شهر:سنة) والوقت (ساعة:دقيقة). إن كنت ستتخصص في قواعد البيانات وستعمل مع أحد أنظمة قواعد البيانات، فيمكنك آنذاك التحقق من توثيقات قاعدة البيانات التي ستستخدمها وما ستوفره من أنواع بيانات يمكن استخدامها، وعمومًا ننصحك بالاطلاع على مقال البيانات في SQL: أنواعها والقيود عليها وانظر أيضًا توثيق أنواع البيانات في لغة SQL العربي من موسوعة حسوب. ملاحظة: تطور حاليًا ما يُدعى بقواعد البيانات الكائنية OODB التي تخزّن بياناتها على شكل كائنات بدلًا من الأنواع الأساسية التي تعرفنا عليها وستجد لنفسها قريبًا مكانًا في عالم البيانات الضخمة المتغير. خاتمة رأينا في هذا المقال أن الأساس المتين للمعرفة البشرية مبني على البيانات التي نستخلصها من بيئتنا المحيطة عند محاولة فهم أو توصيف أو تحليل ما يجري حولنا. لقد حُفظت البيانات على جدران الكهوف وعلى جلود الحيوانات وعلى الأوراق وفي الكتب وصولًا إلى الخوادم المخصصة التي تخزن كميات هائلة من أنواع البيانات وتساعد عبر إمكاناتها التقنية في معالجة هذه البيانات وإيجاد الروابط فيما بينها والحصول على معارف ورؤىً جديدة. تحدثنا أيضًا عن طرق حيازة المعلومات وكيفية تصنيفها، وتعرفنا على الطريقة الرقمية في تخزين واسترجاع البيانات، وفصلنا الشرح في أنواع البيانات في لغات البرمجة وضربنا مختلف الأمثلة عليها لما لها من أهمية كبيرة في فهم أي لغة برمجة تريد أن تتعلمها. وهكذا نكون قد أحطنا ببعض المفاهيم الأساسية التي قد تجدها عونًا لك إن أردت الخوض في مجال البيانات المزدهر وسريع التطور كتحليل البيانات وتصميم قواعدها وتحليل الأنظمة والحوسبة الحدية والتنقيب في البيانات الضخمة أو حتى العمل في البرمجة التي ستعالج البيانات أولًا وآخرًا. اقرأ أيضًا تعلم البرمجة المدخل الشامل لتعلم علوم الحاسوب علم البيانات Data science: الدليل الشامل مفهوم علم البيانات Data Science المرجع الشامل إلى تعلم لغة بايثون1 نقطة
-
يمكنك الذهاب إلى الإعدادات (Settings) ولذهاب إليها من خلال القائمة File ثم نقوم بإختيار العنصر Preferences سوف تظهر لديك خيارات جديدة قم باختيار Settings ، عندها سوف تفتح لديك صفحة الإعدادات ، ضمن الإعدادات يوجد الخيار Editor: Font Size قم بتعديله إلى الحجم الذي تريده . أو إن كنت لا تريد تعديل الخط يمكنك عمل Zoom من خلال (+) + ctrl أو (-) + ctrl لتقليل حجم Zoom .1 نقطة
-
يمكنك فعل ذلك بعدة طرق الاولى : من خلال وضع مؤشر الماوي في أي مكان في الصفحة ومن ثم الضغط على ctrl وتحريك عجلة الماوس للأعلى لتكبير الخط أو للأسفل لتصغير الخط الطريقة الثانية يمكنك تكبير التطبيق بالضغط على ctrl و + أو تصغير التطبيق بالضغط على ctrl و - الطريقة الثالثة من خلال الضغط على زر f1 ومن ثم الضغط كتابة setting ومن ثم اختيار الخيار التالي وسوف تجد بداخله اعدادات التطبيق ومنها حجم الخط وسمكه وغيرها من الاعدادات , ابحث عن editor.fontSize وغير الخط لما تريده1 نقطة
-
هل تستخدم برنامج Vs Code؟ اذا كنت تستخدمه فيمكنك فعل ذلك بطريقتين عن طريق الاختصارات الأولى باستخدام الاختصار ctrl+/ او ctrl+ظ الاختصار الثاني يمكنك من خلال الضغط على alt+shift+A1 نقطة
-
يمكنك تحديد الكود الذي تريد تعليقه (الأسطر الخمسة لديك) وباستخدام الزرين / + ctrl سوف يقوم بتعليق جميع الأسطر المحددة ، قم بالتجربة وأخبرنا بالنتيجة هل نجح معك أو لا1 نقطة
-
شرح المشكلة: عند إستدعاء التابع: bind_param $stmt->bind_param("sssssssssssss", $name,$defaultLang,$section,$workTitle,$hiring,$permission,$imageAdds,$username,$password,$email,$created_at,$created_at,$created_by); يجب أن يُستدعى إنطلاقاً من كائن من النوع mysqli_stmt لكن حالياً يتم إستدعاؤه من خلال متغير يحمل قيمة بوليانية false. أي أن stmt ليس من النوع mysqli_stmt و إنما bool ما يعني أن ما يُعيده السطر: $conn->prepare( "INSERT INTO users(first_name,lang, section, title, hiring, permission, profile_image, username, password, email,created_at,verified_at,created_by) VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?) "); هو false حيث أن تهيئة الإستعلام فشلت لسبب ما.1 نقطة
-
يرجى تحديد نوع الإستضافة ، إذا كانت vps او غير ذلك وأيضا نظام تشغيل الإستضافة ...، حتى نستطيع مساعدتك1 نقطة
-
1 نقطة
-
السلاش / يتعرف عليها في لغات البرمجة أنها علامة القسمة مثلاً 6/2 سيكون الناتج 3 وفي لغات برمجة تستخدم الdouble slash // لكاتبة تعليق في البرنامج ويتم تخطي هذه الكتابة عند التنفيذ وتكون فقط للقراءة مثال : // هذا تعليق في الشيفرة البرمجية في الأسفل يتم تنفيذ أمر طباعة في لغة جافا public static void main(String[] args) { System.out.println("Hello World !"); //print Hello World ! }1 نقطة
-
1 نقطة
-
أثناء قراءة التعليمات الإرشادية لتثبيت تطبيق ما ستصادف غالبًا مصطلحات مثل فلات باك Flatpak وسناب Snap وآب إيماج AppImage، وربما تكون قد استخدمت أحدها على لينكس بدون أن تعلم، فما هي هذه المصطلحات؟ يُعَد كل من فلات باك وسناب وآب إيماج نظامًا شاملًا للتحزيم packaging، وسنخص بالذكر في هذا المقال نظام فلات باك. المشكلات قبل فلات باك يُعَد تثبيت وإدارة البرمجيات أحد أهم جوانب إدارة نظام لينكس، والتي تزداد صعوبتها بسبب وجود العديد من توزيعات لينكس. وعند استخدام الأنظمة التقليدية لإدارة الحزم بتنسيقات تقليدية deb/rpm، كانت تتواجد المشكلات التالية أثناء محاولة تشغيل برنامج ما في النظام: البحث عن المكتبات اللازمة لعمل البرنامج. الاعتماديات، والتي تعني اعتماد البرنامج في عمله على حزم أخرى. الحاجة لتحقيق التوافق مع مدير الحزم الجديد عند التبديل من توزيعة لينكس الأخرى. لا توفر أمانًا كبيرًا لعمليات تثبيت وإدارة البرمجيات. يمكن لمستخدمي لينكس المحترفين إيجاد أفضل طريقة للتغلب على الصعوبات، ولكن بالنسبة للمبتدئين أو المستخدمين الذين لا يمتلكون وقتًا لتعلم إدارة الحزم أو يجدون صعوبةً بتعلمها أو الخبرة بالبحث عن كل خلل وإصلاحه؛ يكون الأمر صعبًا جدًا، وهنا يأتي دور فلات باك. ما هو فلات باك Flatpak بالتفصيل؟ أسّس ألكسندر لارسون Alexander Larsson فلات باك مفتوح المصدر في صيف عام 2007 ليكون نظامًا مُساعدًا لإدارة الحزم ويتيح نشر البرمجيات وتثبيتها وإدارتها، ويتم تثبيت البرمجيات بلا أي مشكلات ودون الحاجة إلى القلق بشأن الاعتماديات أو زمن التنفيذ أو المكتبات التي يحتاجها البرنامج في عمله أو توزيعة لينكس المستخدمة سواءً كانت التوزيعة تعتمد على ديبيان أو آرتش لذلك يوُصف بالنظام الشامل الذي وفر حلولًا لمعظم مشكلات الأنظمة التقليدية. آلية عمل فلات باك تعمل تطبيقات فلات باك في بيئة معزولة sandbox تحتوي على عدة أمور لتلبية متطلبات تشغيل برنامج محدد مثل زمن التنفيذ والمكتبات المجمعة. وبسبب خاصية العزل، لا يمكن لتطبيقات فلات باك أن تجري أي تغييرات على النظام دون إذن من المستخدم، مما يُحسّن أمان النظام. من أين يمكن الحصول على تطبيقات فلات باك؟ لا يمكن استخدام حزم فلات باك بدون أن توفر توزيعة لينكس المستخدمة خاصية دعم فلات باك، وتتوفر هذه الخاصية افتراضيًا في توزيعات معينة مثل فيدورا Fedora وسولس Solus، بينما تحتاج بعض التوزيعات مثل أوبنتو Ubuntu إلى تثبيت خاصية الدعم يدويًا. لا يقيّد فلات باك المستخدم بمصدر واحد للحصول على البرامج، حيث توجد العديد من مستودعات فلات باك وأشهرها المستودع الخارجي فلات هاب Flathub وهو مركز تطبيقات وبرامج أنشأه فريق فلات باك ويمكن من خلاله نشر البرمجيات وإدارتها، وتوضح الصورة التالية الصفحة الرئيسية لموقع فلات هاب: مزايا وعيوب فلات باك يمتلك فلات باك العديد من المزايا والعيوب كغيره من الأنظمة، سنناقش تاليًا العديد من هذه المزايا والعيوب: مزايا استخدام فلات باك يمكن تشغيل تطبيقات فلات باك على أي توزيعة لينكس. يوفر توافقيةً مستقبليةً أي أنه يلغي مشكلة عدم عمل بعض التطبيقات عند ترقية إصدار توزيعة لينكس (فقد لا تدعم بعض التطبيقات التوزيعات الجديدة). يحل مشكلة الاعتماديات. يوفر في بعض الحالات أحدث وأهم إصدار من برنامج ما. لا يقيد المستخدمين بمورد واحد بسبب عدم اعتماد التوزيع على خادم مركزي. يُحسّن أمان النظام بسبب خاصية التطبيقات المعزولة sandboxed applications. يحقق تكامل مريح مع مركز البرمجيات الموجود على توزيعة لينكس. عيوب استخدام فلات باك لا يدعم نسخة الخادم، أي لا تتوفر منه نسخة للخادم، وهو متاح فقط لأجهزة الحاسوب المكتبي بنظام التشغيل لينكس. امتلاء أسرع لمساحة التخزين، حيث تشغل تطبيقات فلات باك مساحة أكبر على القرص مما تشغله عادةً ملفات deb/rpm، مما يوجب إيجاد طريقة لتفريغ مساحة التخزين. تفقد بعض البرمجيات فعاليتها بسبب خاصية العمل في بيئة معزولة، فقد لا تدعم تطبيقات فلات باك مثلًا سمة GTK المخصصة حسب المستخدم. تثبيت فلات باك يكون فلات باك مثبتًا على بعض توزيعات لينكس مثل توزيعات فيدورا ولا يكون مثبتًا على توزيعات أخرى مثل أوبنتو، لذا سنشرح كيفية تثبيته وضبطه على تلك التوزيعة، أما إن كانت توزيعتك التي تستخدمها مختلفة، فاختر من صفحة التثبيت الرسمية لفلات باك توزيعتك وطبق الأوامر. نفذ الأمر التالي في سطر الأوامر لتثبيت فلات باك على توزيعة أوبنتو لديك: sudo apt install flatpak يجب أن يكون إصدار التوزيعة 18.10 وما بعد ليعمل الأمر بنجاح، أو نفذ الأوامر الثلاثة التالية: sudo add-apt-repository ppa:flatpak/stable sudo apt update sudo apt install flatpak نزل إضافة باسم Software Flatpak حتى تتاح إمكانية تثبيت التطبيقات دون الحاجة إلى سطر الأوامر، وذلك بتنفيذ الأمر التالي: sudo apt install gnome-software-plugin-flatpak أضف المستودع Flathub الذي أشرنا إليه سابقًا حتى تتمكن من الوصول إلى التطبيقات وتثبيتها منه: flatpak remote-add --if-not-exists flathub https://flathub.org/repo/flathub.flatpakrepo أعد تشغيل الحاسوب حتى تكتمل عملية التثبيت، وبعدها يمكنك تثبيت التطبيقات، تصفحها من واجهة التطبيق أو جرب تصفح قائمة apps في الموقع الرسمي وثبت التطبيق الذي تريد. استخدام فلات باك عبر سطر الأوامر عمومًا، توفر واجهة فلات باك الرسومية كل ما تريده في عملية إدارة التطبيقات من تثبيت وتحديث وإزالة مثلًا، وهي سهلة ولا تحتاج إلى تفصيل وشرح ونتركك للتعرف عليها بنفسك، ولكن هنالك طريقة أخرى لاستخدام فلات باك وهي عبر واجهة سطر الأوامر وهذا الاستخدام قد يهم بعض المستخدمين خصوصًا من يحبون استعمال سطر الأوامر وليس لعموم المستخدمين كما أشرنا. يعد الأمر flatpak الأمر الأساسي المستخدم ثم تلحق به كافة الأوامر، مثلًا أمر التثبيت يكون flatpak install وأمر الإزالة يكون flatpak uninstall وهكذا. البحث عن تطبيق يمكنك البحث ضمن التطبيقات باستعمال الأمر search، فمثلًا، إن أردت البحث عن تطبيق الرسم GIMP نفذ الأمر التالي: flatpak search gimp سيعيد الأمر أي نتيجة تطابق عبارة البحث، وتمثل تلك النتيجة معرّف التطبيق والمستودع الموجود فيه وهي تفاصيل مهمة لاستعمالها في عملية التثبيت كما يلي. تثبيت تطبيق إن أردت تثبيت تطبيق ما وليكن تطبيق الرسم GIMP الذي بحثنا عنه في الأمر السابق، فاستعمل الأمر التالي: flatpak install flathub org.gimp.GIMP يشير flathub في الأمر إلى المستودع الذي سيثبّت التطبيق منه والجملة التي في آخره org.gimp.GIMP إلى معرف التطبيق وهو GIMP المراد تثبيته، ويتكون المعرف ذاك من 3 أجزاء كما هو واضح آخرها اسم التطبيق. تثبيت أي تطبيق آخر مشابه للعملية ولكن يختلف جزء معرِّف التطبيق أو أحيانًا المستودع المراد تثبيت التطبيق منه أيضًا، وعمومًا وبدءًا من الإصدار 1.2 من فلات باك، أصبح بإمكانك اختصار الأمر السابق بذكر اسم التطبيق فقط كما يلي: flatpak install gimp ستظهر لك رسالة باسم المستودع ومعرف التطبيق لتؤكدها قبل بدء تثبيت التطبيق. أضف إلى ذلك، توفر معلومات التطبيقات المراد تثبيتها عبر ملف .flatpakref والذي يمكن استعماله في عملية التثبيت أيضًا، سواءً بتحديده محليًا إن كان على الحاسوب أو تحديده عبر رابط ويب، مثلًا يمكن تثبيت تطبيق GIMP السابق بهذه الطريقة عبر الأمر التالي: flatpak install https://flathub.org/repo/appstream/org.gimp.GIMP.flatpakref تشغيل تطبيق يمكنك تشغيل التطبيق بمجرد تثبيته كما وضحنا آنفًا باستعمال الأمر run مع معرّف التطبيق كما يلي: flatpak run org.gimp.GIMP تحديث التطبيقات يمكنك تحديث جميع التطبيقات المثبتة عبر فلات باك باستعمال الأمر التالي: flatpak update عرض التطبيقات المثبتة استعمل الأمر التالي لعرض كافة التطبيقات المثبتة: flatpak list --app حذف تطبيق استعمل الأمر التالي لحذف تطبيق مثبّت بتحديد معرّفه: flatpak uninstall org.gimp.GIMP عرضنا إلى هنا الأوامر شائعة الاستخدام ويمكنك الرجوع إلى الموقع الرسمي لمزيد من التفاصيل إن احتجت لها. ترجمة -وبتصرف- للمقال What is Flatpak? لصاحبه Ankush Das. اقرأ أيضًا عرض موجز لأشهر توزيعات لينكس مدخل إلى مستودعات أوبنتو تثبيت نظام لينكس داخل نظام ويندوز في بيئة وهمية عشرون أمرا في لينكس يفترض أن يعرفها كل مدير نظم1 نقطة
-
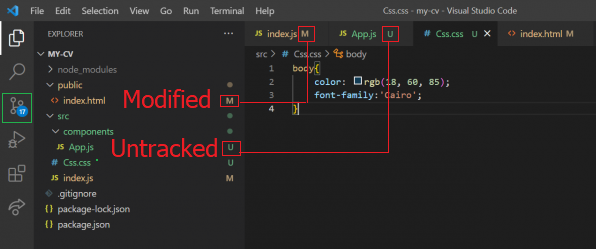
حرف U هو إختصار لكلمة Untracked أي أن هذا الملف غير مسجل في Git ولن يتم تتبع أي تغيرات تجري عليه، بينما حرف M يعني Modified (أي مُعدل)، ولفهم ما تعنيه هذه الكلمات يجب دراسة Git وهو برنامج يستخدم لإدارة الملفات والمشاريع البرمجة، بحيث يمكن عمل أي تغيرات على الملفات وتسجيلها وإرجاع الملفات إلى الحالة التي كانت عليها قبل التعديلات، ويسمح كذلك بأن يكون أكثر من مبرمج بالعمل على المشروع في نفس الوقت (عبر إستخدام GitHub أو GitLab)، بالإضافة إلى عمل أكثر من فرع Branch (نسخة كاملة من المشروع) للعمل عليها (لأصلاح خطأ معين أو لإضافة ميزة جديدة) بشكل سهل للغاية. إن أردت إخفاء حرف U فعليك أن تقوم بتنفيذ الأمر التالي: git add <اسم الملف> مع تغير <اسم الملف> إلى اسم الملف، مثال: git add App.js الأمر السابق سوف يخبر Git بمراقبة الملف App.js وحفظ أي تغيرات تجري عليه. ملاحظة: يجب التأكد من أنك في مجلد المشروع الصحيح عند تنفيذ الأمر السابق لكي يعمل بشكل سليم. هنا فيديو يشرح أهل الأساسيات الخاصة بـ Git: ويمكنك كذلك الإطلاع على العديد من المقالات الخاصة بـ Git من هنا.1 نقطة
-
تأكد من أنك قمت بتنفيذ الأمر التالي: heroku git:remote -a yourapp أيضًا عندما تقوم بعمل push يجب أن تكون في مجلد المشروع الرئيسي (أي لا تقوم بالدخول إلى مجلدات فرعية عبر الأمر cd لأن هذا سيسبب خطأ). إن أستمرت المشكلة حاول تنفيذ الأمر التالي وتأكد من أن تكون النتيجة صحيحة: git remote get-url heroku // نتيجة تنفيذ الأمر السابق كالتالي https://git.heroku.com/app-name.git إن ظهر لك الخطأ error: No such remote 'heroku فقم بتنفيذ الأمر التالي: git remote add heroku https://git.heroku.com/app-name.git git push heroku main مع تغير قيمة app-name باسم المشروع الخاص بك.1 نقطة
-
ربما أخبرك أحدهم من قبل بأنك لا تستطيع أن تُعرِّف الشيء بالإشارة إلى ذاته، ولكن هذا ليس صحيحًا عمومًا؛ فإذا أُنجز هذا التعريف بالصورة الصحيحة، فسيُصبِح مُمكِنًا ويتحول إلى تقنيةٍ فعالةٍ للغاية. التعريف التعاودي recursive لشيءٍ أو لمفهومٍ هو ذلك التعريف الذي يُشير إلى نفسه ضِمْن تعريفه، حيث يُمكِننا مثلًا تعريف السلف ancestor بأن يكون إما أبًا أو سلفًا للأب؛ وفي مثال آخر، تعريف الجملة sentence على أنها مكوَّنة -من بين أشياءٍ أخرى كثيرة- من جملتين مرتبطتين بحرف عطفٍ مثل "و". مثالٌ ثالث هو تعريف المُجلد directory على أنه جزءٌ من قرصٍ صلب disk drive، والذي بدوره قد يحتوي على ملفاتٍ ومجلدات. يُمكِننا أيضًا تعريف المجموعة set بسياق علم الرياضيات على أنها مجموعةٌ من العناصر التي يُمكِنها أن تكون مجموعةً بحد ذاتها. في مثال أخير، يمكن الإشارة إلى إمكانية تعريف التعليمة statement بلغة جافا، على أنها قد تَكُون تَعليمَة while المُكوَّنة بدورها من كلمة while وشرط منطقي وتعليمة. تستطيع التعريفات التعاودية recursive وصف أكثر المواقف تعقيدًا بعدة كلماتٍ قليلة، فإذا أردنا مثلًا تعريف السلف دون استخدام التعاود، فإننا قد نقول أنه "أبٌ، أو جدٌ، أو جدٌ أكبر،… وهكذا". في الحقيقة، ليس واضحًا ما هو المقصود وراء كلمة "إلخ"، حيث قد تقع بنفس المشكلة إذا حاولت تعريف مجلد على أنه ملفٌ مُكوَّنٌ من قائمةٍ من الملفات التي قد يكون بعضها بدوره قائمةً أخرى من الملفات، والتي قد يكون بعضها أيضًا قائمةً من الملفات، وهكذا". حاول وصف مصطلح تعليمة جافا statement دون استخدام التعاود، وسترى أنه أمرٌ غايةٌ في الصعوبة. يُمكِننا في الواقع استخدام التعاود مثل تقنيةٍ برمجية، فعلى سبيل المثال البرنامج الفرعي التعاودي recursive subroutine، أو التابع التعاودي recursive method هو ذلك البرنامج أو التابع الذي يُعاود استدعاء ذاته استدعاءً مباشرًا أو غير مباشر. ويعني الاستدعاء المباشر احتواء تعريف البرنامج الفرعي على تعليمة استدعاء برنامجٍ فرعي للبرنامج ذاته قيد التعريف؛ أما الاستدعاء غير المباشر فيعني استدعاء البرنامج الفرعي لبرنامجٍ فرعيٍ ثانٍ، والذي بدوره يستدعي البرنامج الفرعي الأول استدعاءً مباشرًا أو غير مباشر. تستطيع البرامج الفرعية التعاودية التي تتمكن من معاودة استدعاء ذاتها، أن تُعرِّف بعض المهمات المعقدة بعدة أسطر من الشيفرة. سنناقش بالجزء المتبقي من هذا المقال عدة أمثلة على ذلك، كما سنتعرَّض لأمثلةٍ أخرى خلال المقالات المتبقية من هذه السلسلة. بحث ثنائي تعاودي Recursive Binary Search لنبدأ بمثال خوارزمية البحث الثنائي binary search الذي تَعرَّضنا له بمقال البحث والترتيب في المصفوفات Array في جافا، حيث يُستخدم البحث الثنائي للعثور على قيمةٍ مُحدَّدةٍ ضِمْن قائمةٍ مُرتَّبةٍ من العناصر في حالة وجودها ضِمْن تلك القائمة. وتتمحور فكرة الخوارزمية حول فحص عنصر منتصف القائمة، فإذا كان ذلك العنصر يُساوِي القيمة المطلوبة، فإننا نَكُون قد انتهينا بالفعل؛ أما إذا كانت القيمة المطلوبة أقل من قيمة عنصر منتصف القائمة، فإننا نبحث عن تلك القيمة بالنصف الأول من القائمة؛ أما إن لم تَكْن كذلك، فإننا نبحث عنها بالنصف الثاني من القائمة. يُطلق اسم البحث الثنائي binary search على الأسلوب المُتبَّع للبحث عن قيمةٍ ضِمْن النصف الأول أو الثاني من قائمة؛ أي أن نَفْحَص عنصر منتصف القائمة الذي ما يزال قيد البحث، وبناءً على ذلك إما نَجِد القيمة التي نبحث عنها أو أن نضطَّر إلى إعادة تطبيق البحث الثنائي على النصف المُتبقي من عناصر القائمة. يُعدّ هذا توصيفًا تعاوديًا، ولهذا يُمكِننا تنفيذه بكتابة برنامجٍ فرعيٍ تعاودي recursive subroutine. قبل كتابة ذلك البرنامج، يجب علينا أخذ نقطتين مهمتين بالحسبان تُمثِلان حقائقًا عامةً عن البرامج الفرعية التعاودية. النقطة الأولى: تبدأ خوارزمية البحث الثنائي بفحص عنصر منتصف القائمة، ولكن ما الذي سيحدُث إذا كانت تلك القائمة فارغة؟ ببساطة، إذا لم jكْن هناك أي عناصر ضمن القائمة، فسيستحيل بالتأكيد فحص عنصر منتصف تلك القائمة. كنا قد أضفنا شرطًا مُسبقًا precondition بمقال كيفية كتابة برامج صحيحة باستخدام لغة جافا ينص على ضرورة أن تَكُون القائمة غير فارغة. وبناءً على ذلك، علينا تعديل الخوارزمية، بحيث تأخذ هذا الشرط المُسبَّق بالحسبان. وينقلنا هذا إلى السؤال التالي. النقطة الثانية: ما الذي ينبغي أن نفعله في تلك الحالة؟ الإجابة بسيطة، فإذا كانت القائمة فارغة، فيُمكِننا ببساطة استنتاج أن القيمة التي نبحث عنها غير موجودةٍ بالقائمة، أي أنه يُمكِننا إعادة الإجابة دون الحاجة لإجراء أي عملٍ آخر. يُعدّ وصولنا لقائمةٍ فارغة وفقًا لخوارزمية البحث الثنائي حالةً أساسيةً base case؛ حيث أن الحالة الأساسية لخوارزمية تعاودية، هي تلك الحالة المُمكن مُعالجتها مباشرةً دون الحاجة لإعادة تطبيق الخوارزمية تطبيقًا تعاوديًا. بالإضافة إلى ذلك، يُعدّ العثور على القيمة المطلوبة بعنصر منتصف القائمة وفقًا لخوارزمية البحث الثنائي حالةً أساسيةً أخرى، حيث نكون قد انتهينا دون الحاجة لأي إجراءٍ تعاوديٍ آخر. تتعلَّق النقطة الثانية بمعاملات parameters البرنامج الفرعي، حيث تُصاغ المشكلة عادةً بكوننا نبحث عن قيمةٍ معينة ضمن قائمة، وتستقبل النسخة الأصلية غير التعاودية non-recursive من برنامج البحث الثنائي تلك القائمة على أنها مصفوفة. في المقابل، لابُدّ أن تُمكِّننا النسخة التعاودية من تطبيق البرنامج الفرعي تطبيقًا تعاوديًا على جزءٍ معينٍ من القائمة الأصلية. بصياغةٍ أخرى، إذا كان البرنامج الفرعي الأصلي مُصمَّمًا للبحث ضمن كامل المصفوفة، فلا بُدّ للبرنامج الفرعي التعاودي أن يَكُون قادرًا على البحث ضِمْن جزءٍ معينٍ من المصفوفة، وبناءً على ذلك لا بُدّ أن يستقبل البرنامج الفرعي معاملاتٍ تُحدِّد ذلك الجزء من المصفوفة الذي ينبغي البحث ضمنه. ولكي تَكُون قادرًا على حل مشكلةٍ معينة حلًا تعاوديًا، فعادةً ما يَكُون من الضروري تَعمِيم المشكلة بعض الشيء. يوضح المثال التالي خوارزمية البحث الثنائي التعاودي التي تبحث عن قيمة مُحدٍَّدة ضمن جزءٍ من مصفوفة أعداد صحيحة. static int binarySearch(int[] A, int loIndex, int hiIndex, int value) { if (loIndex > hiIndex) { // 1 return -1; } else { // 2 int middle = (loIndex + hiIndex) / 2; if (value == A[middle]) return middle; else if (value < A[middle]) return binarySearch(A, loIndex, middle - 1, value); else // لابُدّ أن تكون القيمة أكبر من [A[middle return binarySearch(A, middle + 1, hiIndex, value); } } // end binarySearch() [1] جاء موضع البداية لنطاق البحث قبل موضع نهايته؛ أي ليس هناك أي عناصرٍ فعليةٍ ضمن ذلك النطاق، مما يعني أن القيمة غير موجودةٍ بالقائمة الفارغة. [2] انظر للموضع بمنتصف القائمة، فإذا كانت القيمة بذلك الموضع، أعِد هذا الموضع؛ أما إذا لم تكن، فابحث بالنصف الأول أو الثاني من القائمة بحثًا تعاوديًا. يُحدِّد المعاملان loIndex وhiIndex بالبرنامج الفرعي السابق جزء المصفوفة المطلوب البحث فيه. لاحظ أنه ما يزال بإمكاننا استدعاء binarySearch(A, 0, A.length - 1, value) للبحث ضمن المصفوفة بأكملها. في حال وقوع أي من الحالتين الأساسيتين base cases، أي عند عدم وجود أي عناصرٍ أخرى ضمن النطاق المخصص من فهارس المصفوفة، أو عندما تكون القيمة بمنتصف النطاق المُخصَّص هي نفسها القيمة المطلوب العثور عليها؛ فيمكن عندها للبرنامج الفرعي إعادة الإجابة تلقائيًا دون اللجوء إلى التعاود؛ بينما يضطر في الحالات الأخرى إلى الاستدعاء التعاودي recursive call لحساب الإجابة ثم يعيدها. يواجه الكثير من المبرمجين في البداية صعوبةً ليدركوا أن التعاود يعمل بنجاح فعليًا، حيث تَكمُن الفكرة في تَحقُّق أمرين لضمان عمل التعاود بالشكل السليم، أولهما أنه لا بُدّ من تخصيص واحدةٍ أو أكثر من الحالات الأساسية base cases المُمكِن معالجتها تلقائيًا دون اللجوء إلى التعاود. ثانيًا، عند تطبيق التعاود أثناء حل المشكلة، فلا بُدّ أن تكون المشكلة أصغر بطريقةٍ ما بكل مرة؛ وبتعبيرٍ آخر، لابُدّ أن تكون المشكلة بكل مرةٍ أقرب إلى واحدةٍ من الحالات الأساسية بالموازنة مع المشكلة الأصلية. يَعنِي ما سبق أنه إذا كنا نستطيع حلّ نُسخٍ أصغر من مشكلةٍ معينة، وكذلك تَقسِيم النسخ الكبيرة من تلك المشكلة إلى نسخٍ أصغر، فيمكننا حل تلك المشكلة مهما بلغ حجمها. وفي النهاية، سنتمكَّن من تقسيم النسخة الكبيرة من المشكلة عبر عدة خطوات إلى النسخة الأصغر من المشكلة؛ أي إلى واحدةٍ من الحالات الأساسية. في الواقع، يتطلّب ذلك الاحتفاظ بقدرٍ هائلٍ من التفاصيل، ولكن لحسن الحظ لست مطالبًا بإجراء أي من ذلك يدويًا، حيث يُجرِيه الحاسوب بدلًا منك. في المقابل، عليك فقط تحديد الخطوط العريضة أي الحالات الأساسية وكيفية تقسيم المشكلة الكبيرة إلى مشكلاتٍ صغيرة. يُجري الحاسوب كل ما هو مطلوب لتقسيم المشكلة الكبيرة إلى مشكلاتٍ أصغر عبر كثيرٍ من الخطوات، حتى يَصِل إلى أيٍ من الحالات الأساسية. ستدفعك محاولة التفكير بكيفية إجراء عملية التقسيم تفصيليًا إلى الجنون، وستشعر أن التعاود عمليةً معقدةً وصعبة، لكنه في الحقيقة أسلوبٌ رائعٌ وفعال، وعادةً ما يُعدّ الطريقة الأبسط لحل المشكلات المُعقدة. تذكَّر دومًا القاعدتين الأساسيتين: لا بُدّ من تخصيص واحدة أو أكثر من الحالات الأساسية base cases. لا بُدّ من تطبيق البرنامج الفرعي تطبيقًا تعاوديًا recursively على مشكلاتٍ أصغر من المشكلة الأصلية. يُعدّ انتهاك أي من هاتين القاعدتين أخطاءً شائعةً أثناء كتابة البرامج الفرعية التعاودية، وينتج عن انتهاك أي من القاعدتين عادةً حدوث تعاودٍ لا نهائي infinite recursion؛ أي يستمر البرنامج الفرعي باستدعاء نفسه مرةً بعد أخرى بصورةٍ لانهائية دون الوصول أبدًا إلى حالة أساسية. يتشابه التعاود اللانهائي نوعًا ما مع التكرار اللانهائي infinite loop، ولكنه يستهلك أيضًا من ذاكرة الحاسوب؛ حيث تتطلَّب كل عملية استدعاء تعاودي recursive call جزءًا من الذاكرة، وبالتالي ستَنفُد الذاكرة لدى الوقوع بتعاودٍ لا نهائي، ثم ينهار crash البرنامج، حيث ينهار البرنامج نتيجةً لحدوث اعتراض exception من النوع StackOverflowError بلغة جافا تحديدًا. مشكلة أبراج هانوي Hanoi درسنا حتى الآن خوارزمية البحث الثنائي، والتي يُمكِن تنفيذها بسهولة باستخدام حلقة while بدلًا من التعاود. سنتناول الآن مشكلةً يسهُل حلّها بالتعاود ويَصعُب بدونه، وهي مثالٌ نموذجيٌ يُعرَف باسم مشكلة أبراج هانوي The Towers of Hanoi، حيث تتكوَّن المشكلة من مجموعة أقراصٍ مختلفة الحجم موضوعةٍ على قاعدة بترتيبٍ تنازلي، والمطلوب هو تحريك مجموعة الأقراص من مكدسٍ Stack إلى آخر وفقًا لشرطين، هما: يُمكِن تحريك قرصٍ واحدٍ فقط بكل مرة. لا يُمكِن أبدًا وضع قرصٍ معينٍ فوق آخر أصغر منه. هناك أيضًا قرصٌ إضافيٌ ثالث يُمكِنك استخدامه، حيث يُظهِر النصف الأعلى من الصورة التالية الحالة المبدئية لعشرة أقراص، بينما يُوضِح النصف السفلي حالة الأقراص بعد إجراء عدة حركات. الصورة التالية مأخوذة من البرنامج التوضيحي TowersOfHanoiGUI.java الذي سنتعرض له جزئية لاحقة من هذه السلسلة، حيث سننشئ خلال ذلك البرنامج صورةً متحركةً animation لحل هذه المشكلة خطوةً بخطوة. تكمن المشكلة ببساطة في تحريك عشرة أقراصٍ من المكدس 0 إلى المكدس 1 وفقًا للشروط المذكورة أعلاه، ويُمكِن أيضًا استخدام المكدس 2 بمثابة موضعٍ مؤقت. يقودنا ذلك إلى السؤال التالي: هل يُمكننا تقسيم هذه المشكلة إلى مشكلاتٍ أصغر من نفس النوع أي تعميم المشكلة قليلًا؟ من البديهي أن يكون حجم المشكلة هو عدد الأقراص المطلوب تحريكها، فإذا كان هناك عدد N من الأقراص بالمكدس 0، فإننا نعرف أنه سيكون علينا بالنهاية تحريك القرص السفلي من المكدس 0 إلى المكدس 1. مع ذلك وفقًا للشروط، فلا بُدّ أن يكون أول عددٍ N-1 من الأقراص في المكدس 2، وبمجرد أن نُحرِّك القرص N إلى المكدس 1، فسيكون علينا تحريك عدد N-1 من الأقراص من المكدس 2 إلى المكدس 1 لإكمال الحل. لاحِظ أن مشكلة تحريك عدد N-1 من الأقراص هي من نفس نوع المشكلة الأصلية أي تحريك عدد Nمن الأقراص، باستثناء أنها نسخةٌ أصغر من المشكلة، حيث يُمثل ذلك بالضبط ما نريده لإجراء التعاود. علينا تعميم المشكلة قليلًا، حيث تتطلب المشكلات الأصغر تحريك الأقراص من المكدس 0 إلى المكدس 2، أو من المكدس 2 إلى المكدس 1، بدلًا من مجرد تحريكها من المكدس 0 إلى المكدس 1، وذلك يعني وجوب تمرير كلٍ من مكدس المصدر والوجهة إلى البرنامج الفرعي التعاودي المسؤول عن حل المشكلة. على الرغم من أن ذلك سيُمكِّننا من تحديد المكدس الاحتياطي ضمنيًا، إلا أنه سيبقى من المريح تمرير المكدس الاحتياطي صراحةً للبرنامج. ويُمثِل وجود قرص واحد فقط الحالة الأساسية، كم سيكون الحل ببساطة في هذه الحالة هو تحريك القرص ضمن خطوةٍ واحدة. تطبع شيفرة البرنامج الفرعي التالي تعليمات حل المشكلة تفصيليًا خطوةً بخطوة. static void towersOfHanoi(int disks, int from, int to, int spare) { if (disks == 1) { // هناك قرصٌ واحدٌ فقط للتحريك. عليك فقط أن تُحرِكه System.out.printf("Move disk 1 from stack %d to stack %d%n", from, to); } else { // 1 towersOfHanoi(disks-1, from, spare, to); System.out.printf("Move disk %d from stack %d to stack %d%n", disks, from, to); towersOfHanoi(disks-1, spare, to, from); } } [1] حَرِّك جميع الأقراص باستثناء قرصٍ واحدٍ فقط إلى المكدس الاحتياطي، ثم حرِّك القرص السفلي وضَع بقية الأقراص الأخرى فوقه. يعبِّر هذا البرنامج الفرعي عن الحل التعاودي البديهي، حيث يشتمل الاستدعاء التعاودي بكل مرةٍ على عددٍ أقل من الأقراص، كما أنه يُمكِن حل المشكلة بسهولةٍ في حالتها الأساسية base case؛ أي عند وجود قرصٍ واحدٍ فقط. لحل مشكلة تحريك عدد N من الأقراص من المكدس 0 إلى المكدس 1، ينبغي استدعاء البرنامج الفرعي على النحو التالي TowersOfHanoi(N,0,1,2)، ويُبيِّن لنا ما يلي خَرْج البرنامج الفرعي عند ضَبْط عدد الأقراص ليُساوِي 4. Move disk 1 from stack 0 to stack 2 Move disk 2 from stack 0 to stack 1 Move disk 1 from stack 2 to stack 1 Move disk 3 from stack 0 to stack 2 Move disk 1 from stack 1 to stack 0 Move disk 2 from stack 1 to stack 2 Move disk 1 from stack 0 to stack 2 Move disk 4 from stack 0 to stack 1 Move disk 1 from stack 2 to stack 1 Move disk 2 from stack 2 to stack 0 Move disk 1 from stack 1 to stack 0 Move disk 3 from stack 2 to stack 1 Move disk 1 from stack 0 to stack 2 Move disk 2 from stack 0 to stack 1 Move disk 1 from stack 2 to stack 1 يُبيِّن خَرْج البرنامج بالأعلى تفاصيل حل المشكلة، ولست بحاجةٍ إلى التفكير بطريقة الحل تفصيليًا، حيث من الصعب جدًا تتبُّع تفاصيل عمل الخوارزميات التعاودية بدقة على الرغم من سهولتها وأناقتها، وسيتولى الحاسوب عمومًا مهمة تنفيذ كل تلك التفاصيل. قد تفكر بما سيحدث في حال عدم تحقُّق الشرط المُسبَق precondition، الذي ينص على أن يكون عدد الأقراص موجبًا، حيث سيؤدي ذلك ببساطة إلى حدوث تعاودٍ لا نهائي infinite recursion. هناك قصةٌ متداولةٌ تشرح السبب وراء تسمية مشكلة أبراج هانوي بذلك الاسم. وفقًا لتلك القصة أُعطيَ مجموعةٌ من الرهبان المتواجدون ببرجٍ معزول قرب هانوي عدد 64 من الأقراص، وطُلِبَ منهم تحريك قرصٍ واحدٍ يوميًا وفقًا لنفس شروط المشكلة بالأعلى؛ وفي اليوم الذي سيكملون فيه تحريك جميع الأقراص من مكدسٍ إلى آخر، سينتهي الكون، لكن لا داعي للقلق، حيث ما يزال أمامنا الكثير من الوقت؛ فعدد الخطوات المطلوبة لحل مشكلة أبراج هانوي لعدد N من الأقراص هو 2N-1 أي 264-1 أي ما يَقرُب من 50,000,000,000,000 سنة. وفقًا لما تطرقنا له في المقال السابق، فإن زمن تشغيل run time خوارزمية أبراج هانوي هو Θ(2n)، حيث تُمثِل n عدد الأقراص المطلوب تحريكها، ونظرًا لنمو الدالة الأسية 2n بسرعةٍ كبيرة، فإنه من الممكن عمليًا حل مشكلة أبراج هانوي لعددٍ صغيرٍ من الأقراص فقط. بالإضافة إلى برنامج حل مشكلة أبراج هانوي بالأعلى، هناك أيضًا برنامجين توضيحين آخرين قد ترغب بإلقاء نظرةٍ عليهما، حيث يوفر كل برنامجٍ منهما توضيحًا مرئيًا لخوارزمية تعاودية. البرنامج الأول هو برنامج Maze.java، والذي يَستخدِم التعاود لحل متاهة؛ أما البرنامج الآخر فهو برنامج LittlePentominos.java، الذي يَستخدِم التعاود لحل نوعٍ معروفٍ من الألغاز. في الحقيقة، تستخدم الشيفرة المصدرية لتلك البرامج بعض التقنيات التي لن نتعرَّض الآن، ومع ذلك سيكون من المفيد أن تُشغِّلها وتشاهدها قليلًا. يُنشِئ البرنامج الأول متاهةً عشوائيةً، ثم يُحاول أن يحل تلك المتاهة بالعثور على مسارٍ عبر المتاهة من ركنها الأيسر العلوي إلى ركنها الأيمن السفلي. في الواقع، تتشابه مشكلة المتاهة كثيرًا مع مشكلة عدّ الكائنات blob-counting، التي سنتعرَّض لها لاحقًا ضمن هذا المقال، حيث يبدأ برنامج حل مشكلة المتاهة التعاودي من مربعٍ معين، ويَفْحَص جميع المربعات المجاورة من خلال إجراء استدعاءٍ تعاودي، وينتهي التعاود إذا تَمكَّن البرنامج من الوصول إلى الركن الأيمن السفلي للمتاهة. في حال لم يتمكَّن البرنامج من العثور على حلٍ من مربعٍ معين، فإنه سيَخرُج من ذلك المربع ويحاول بمكانٍ آخر. يشيع استخدام ذلك الأسلوب ويُعرَف باسم التتبع الخلفي التعاودي recursive backtracking. يُعدّ البرنامج الآخر LittlePentominos تنفيذًا للغزٍ تقليدي، حيث أن pentomino هو شكلٌ متصلٌ مُكوَّنٌ من خمسة مربعات متساوية الحجم. هناك بالتحديد 12 شكلًا محتملًا يُمكن تكوينه بتلك الطريقة بدون عدّ الانعكاسات أو الدورانات المحتملة للأشكال، والمطلوب هو وضع الأشكال الاثنى عشر داخل لوحة 8x8 مملوءة مبدئيًا بأربعة من تلك الأشكال. يفحص الحل التعاودي اللوحة المملوءة جزئيًا، كما يفحص جميع الأشكال المتبقية واحدةً تلو الأخرى، ويُحاول أن يضعها بالموضِع المتاح التالي من اللوحة؛ فإذا كان الموضع مناسبًا، فإنه يعاود استدعاء ذاته استدعاءً تعاوديًا لإكمال الحل؛ أما إذا فشل أثناء ذلك، فإنه سينتقل إلى الشكل التالي. لاحِظ أن ذلك يُعدّ مثالًا آخر على أسلوب التتبع الخلفي التعاودي، وستجد في بنتومينوس نسخةً أعم من البرنامج بميزاتٍ أخرى متعددة. خوارزمية ترتيب تعاودي سنناقش الآن كيفية كتابة خوارزميةٍ تعاوديةٍ لترتيب مصفوفة، وربما يُعَد هذا البرنامج الأكثر عمليًا حتى الآن. لقد تعرَّضنا لخوارزميتي الترتيب بالإدراج insertion sort والترتيب الانتقائي selection sort بمقال البحث والترتيب في المصفوفات Array في جافا، وعلى الرغم من سهولة هاتين الخوارزميتين وبساطتهما، إلا أنهما بطيئتان عند تطبيقهما على المصفوفات الكبيرة. في الواقع، تتوفَّر خوارزمياتٌ أخرى أسرع لترتيب المصفوفات، مثل الترتيب السريع Quicksort؛ التي أثبتت كونها واحدةً من أسرع خوارزميات الترتيب بغالبية الحالات، وهي في الواقع خوارزميةٌ تعاودية recursive algorithm. تعتمد خوارزمية الترتيب السريع Quicksort على فكرةٍ بسيطةٍ وذكية، فإذا كانت لدينا قائمةٌ من العناصر، فسنختار أي عنصر منها وسنُطلِق عليه اسم المحور pivot، حيث يُستخدم العنصر الأول مثل محور، وبعد ذلك سنُحرِك جميع العناصر التي قيمتها أصغر من قيمة المحور إلى بداية القائمة، كما سنُحرِك جميع العناصر التي قيمتها أكبر من قيمة المحور إلى نهاية القائمة. في الأخير، سنضع المحور بين مجموعتي العناصر، وبذلك نكون قد وضعنا المحور بموضعه الصحيح الذي ينبغي أن يحتله بالمصفوفة النهائية المُرتَّبة بالكامل؛ أي أننا لن نحتاج إلى تحريكه مجددًا، وسنُشير إلى تلك العملية باسم QuicksortStep. يُمكنك بسهولة أن ترى أن العملية السابقة QuicksortStep ليست تعاودية، وإنما تُستخدم فقط من قِبل خوارزمية الترتيب السريع Quicksort. تعتمد سرعة الخوارزمية الأساسية على كتابة تنفيذ سريع لعملية QuicksortStep، ونظرًا لأن تلك العملية ليست محور المناقشة، فإننا سنكتفي بعرض تنفيذٍ لها دون مناقشتها تفصيليًا. انظر الشيفرة التالية: static int quicksortStep(int[] A, int lo, int hi) { int pivot = A[lo]; // Get the pivot value. // 0 while (hi > lo) { // Loop invariant (See Subsection Subsection 8.2.3): A[i] <= pivot // for i < lo, and A[i] >= pivot for i > hi. while (hi > lo && A[hi] >= pivot) { // 1 hi--; } if (hi == lo) break; // 2 A[lo] = A[hi]; lo++; while (hi > lo && A[lo] <= pivot) { // 3 lo++; } if (hi == lo) break; // 4 A[hi] = A[lo]; hi--; } // end while // 5 A[lo] = pivot; return lo; } // end QuicksortStep [0] تُحدِّد الأعداد hi وlo نطاق الأعداد المطلوب فحصها. اُنقُص العدد hi وزِد العدد lo حتى يُصبحِا متساويين، وحرِّك الأعداد التي قيمتها أكبر من قيمة المحور بحيث تقع قبل hi، وحرِّك أيضًا الأعداد التي قيمتها أقل من قيمة المحور، بحيث تقع بعد lo. بالبداية، سيكون الموضع A[lo] متاحًا لأن قيمته قد نُسخَت إلى المتغير المحلي pivot. [1] حرِك hi للأسفل بعد الأعداد الأكبر من قيمة المحور، ولاحِظ أنه ليست هناك حاجةً لتحريك أيٍ من تلك الأعداد. [2] العدد A[hi] أقل من قيمة المحور، ولذلك يُمكِنك تحريكه إلى المساحة المتاحة A[lo]، وبالتالي سيُصبِح الموضع A[hi] مُتاحًا. [3] حرِك lo للأعلى قبل الأعداد الأقل من قيمة المحور. لاحِظ أنه ليس هناك حاجةً لتحريك أيٍ من تلك الأعداد. [4] العدد A[lo] أكبر من قيمة المحور، لذلك حرِكه إلى المساحة المتاحة A[hi] وبالتالي سيُصبِح الموضع A[lo] متاحًا. [5] ستُصبِح قيمة lo مساويةً لقيمة hi بهذه النقطة من البرنامج، كما ستتبقَّى مساحةٌ متاحةٌ لذلك الموضع بين الأعداد الأقل من قيمة المحور والأعداد الأكبر منه. ضع المحور بذلك المكان ثم أعِد موضعه. بمجرد حصولنا على التنفيذ السابق لعملية QuicksortStep، ستُصبِح خوارزمية الترتيب السريع Quicksort لترتيب قائمة من العناصر بسيطةً جدًا؛ فهي تتكوَّن من مجرد تطبيق عملية QuicksortStep على تلك القائمة، ثم تطبيق الخوارزمية تطبيقًا تعاوديًا على العناصر الواقعة على كلٍ من يسار الموضع الجديد للمحور ويمينه. سنحتاج أيضًا إلى تخصيص الحالات الأساسية base cases، وفي حال احتواء القائمة على عنصرٍ واحدٍ فقط أو عدم احتوائها على أية عناصر، فذلك يعني أنها مُرتَّبة فعلًا، أي لا حاجة لأي إجراءٍ تعاوديٍ آخر. static void quicksort(int[] A, int lo, int hi) { if (hi <= lo) { // 1 return; } else { // 2 int pivotPosition = quicksortStep(A, lo, hi); quicksort(A, lo, pivotPosition - 1); quicksort(A, pivotPosition + 1, hi); } } [1] طول القائمة يُساوي 0 أو 1، لذلك لسنا بحاجةٍ إلى أي إجراءاتٍ أخرى. [2] سنُطبِّق عملية quicksortStep للحصول على موضع المحور الجديد، ثم سنُطبِّق عملية quicksort تعاوديًا لترتيب تلك العناصر التي تسبق المحور، وتلك التي تليه. كان تعميم المشكلة ضروريًا، حيث كانت المشكلة الأصلية هي ترتيب كامل المصفوفة، بينما ضُبطَت الخوارزمية التعاودية recursive algorithm، بحيث تُصبِح قادرةً على ترتيب جزءٍ معينٍ من المصفوفة. يُمكنك استخدام البرنامج الفرعي quickSort() لترتيب مصفوفةٍ بأكملها من خلال استدعاء quicksort(A, 0, A.length - 1). تُعدّ خوارزمية الترتيب السريع Quicksort مثالًا شيقًا على تحليل الخوارزميات analysis of algorithms؛ لأن زمن تنفيذ الحالة الوسطى average case يختلف تمامًا عن زمن تنفيذ الحالة الأسوأ worst case. سنتناول هنا تحليلًا عاميًا informal للخوارزمية، فبالنسبة للحالة الوسطى، ستُقسِّم عملية quicksortStep المشكلة إلى مشكلتين فرعيتين ويكون حجمهما في المتوسط متساويًا؛ وذلك يعني أننا نُقسِّم مشكلةً بحجم 'n' إلى مشكلتين بحجم 'n/2' تقريبًا، ثم نُقسِّمهما إلى أربع مشكلات بحجم 'n/4' تقريبًا، وهكذا. نظرًا لأن حجم المشكلة يقل إلى النصف في كل مرحلة، فسيكون لدينا عدد log(n) من المراحل. يتناسب القدر المطلوب من المعالجة بكل مرحلةٍ من تلك المراحل مع 'n'؛ أي تُفحَص بالمرحلة الأولى جميع عناصر المصفوفة ويُحتمَل تحريكها. ستكون لدينا بالمرحلة الثانية مشكلتين فرعيتين، حيث تقع جميع عناصر المصفوفة عدا واحدٍ ضمن واحدةٍ من المشكلتين، وبالتالي ستُفحَص جميع تلك العناصر ويُحتمَل تحريكها، وبذلك يكون لدينا إجماليًا عدد n من الخطوات في كلتا المشكلتين الفرعيتين. بالمرحلة الثالثة، ستكون لدينا أربعة مشكلات فرعية وعدد n من الخطوات، وهذا يعني أن لدينا عدد log(n) من المراحل تقريبًا؛ حيث تشتمل كل مرحلةٍ على عدد n من الخطوات، ولهذا يكون زمن تشغيل الحالة الوسطى average case لخوارزمية الترتيب السريع هو Θ(n*log(n)). يَفترِض هذا التحليل تقسيم عملية quicksortStep المشكلة إلى أجزاءٍ متساويةٍ تقريبيًا. وفي الحالة الأسوأ worst case، سيُقسِّم كل تطبيق لعملية quicksortStep مشكلةً بحجم n إلى مشكلتين، حيث تكون الأولى بحجم 0 والأخرى بحجم n-1. يحدث ذلك عندما يكون موضع عنصر المحور ببداية أو نهاية المصفوفة بعد الترتيب، وفي هذه الحالة سيكون لدينا عدد n من المراحل، ويكون زمن تشغيل الحالة الأسوأ هو Θ(n<sup>2</sup>). يندر وقوع الحالة الأسوأ؛ حيث تعتمد على أن تَكون عناصر المصفوفة مُرتَّبةً بطريقةٍ خاصةٍ جدًا، لذلك يُعدّ متوسط أداء خوارزمية الترتيب السريع Quicksort في العموم جيدًا جدًا، باستثناء بعض الحالات النادرة. يُعدّ كَوْن المصفوفة مُرتَّبة بالكامل أو تقريبًا، واحدةً من تلك الحالات النادرة، وإذا أردنا توخّي الدقة، فهي ليست بتلك الحالة النادرة عمليًا. سيستغرق تطبيق خوارزمية الترتيب السريع المُوضَّحة أعلاه على مصفوفةٍ كبيرةٍ مُرتَّبة وقتًا طويلًا، ويُمكِننا في الغالب تَجنُّب حدوث ذلك باختيار موضع المحور عشوائيًا بدلًا من استخدام العنصر الأول دائمًا. تتوفَّر خوازرميات ترتيبٍ أخرى بزمن تشغيلٍ يُساوِي Θ(n*log(n)) بالحالتين الأسوأ والوسطى؛ واحدةٌ منها هي خوارزمية الترتيب بالدمج MergeSort، والتي تُعدّ من الخوارزميات سهلة الفهم، ويُمكِنك البحث عنها إذا كنت مهتمًا. عد الكائنات Blob سنفحص الآن مثالًا آخرًا، حيث سنَعُدّ خلاله عدد المربعات الموجودة ضمن تكتلٍ من المربعات المتصلة، وسنُطلِق على ذلك التكتل اسم كائن blob. يعرض البرنامج التوضيحي Blobs.java شبكةً grid من المربعات الصغيرة مُلوّنةً بالأبيض والرمادي والأحمر. وتُظهِر الصورة التالية لقطة شاشةٍ من البرنامج، والتي يُمكِنك أن ترى خلالها شبكة المربعات مع بعض أزرار التحكم. تُعدّ المربعات الحمراء والرمادية مملوءةً أما المربعات البيضاء فهي فارغة. سنُعرِّف الكائن blob لهذا المثال على النحو التالي: يتكوَّن أي كائنٍ من مربعٍ معين مملوءٍ، بالإضافة إلى جميع المربعات المملوءة التي يُمكِن الوصول إليها من خلال ذلك المربع الأصلي، وذلك عن طريق خلال التحرك لأعلى، أو لأسفل، أو لليمين، أو لليسار عبر مربعاتٍ مملوءةٍ أخرى. إذا نقر المُستخدِم على أي مربعٍ مملوءٍ بالبرنامج، فسيَعُدّ الحاسوب عدد المربعات التي يشتملها الكائن المُتضمِّن للمربع المنقور عليه، وسيُبدِّل لون تلك المربعات إلى الأحمر، حيث أظهرت الصورة السابقة إحدى الكائنات باللون الأحمر. يُوفِّر البرنامج أيضًا أزرار تحكم أخرى مثل زر كائنات جديدة New Blobs، الذي يؤدي النقر عليه إلى إنشاء نمطٍ عشوائي جديدٍ بالشبكة، كما تتوفَّر أيضًا قائمةٌ لتخصيص النسبة التقريبية للمربعات التي ينبغي ملؤها بالنمط الجديد، حيث ستؤدي زيادة تلك النسبة إلى الحصول على كائناتٍ بأحجام أكبر. إلى جانب ما سبق، يتوفَّر أيضًا زر عدّ الكائنات Count the Blobs، الذي سيحسُب بطبيعة الحال عدد الكائناتٍ المختلفة الموجودة بالنمط. يعتمد البرنامج على التعاود recursion لحساب عدد المربعات التي يحتويها كائنٌ blob معين؛ فإذا لم يستخدم البرنامج التعاود، فستكون المهمة صعبة التنفيذ. على الرغم من تسهيل التعاود لحل تلك المشكلة نسبيًا، فما يزال من الضروري استخدام تقنيةٍ أخرى جديدة يشيع استخدامها بعددٍ من التطبيقات الأخرى. سنُخزِّن بيانات شبكة المربعات بمصفوفةٍ ثنائية الأبعاد من القيم المنطقية boolean boolean[][] filled; تكون قيمة filled[r][c] مساويةً للقيمة المنطقية true إذا كان المربع بالصف r والعمود c مملوءًا. وسنُخزِّن عدد صفوف الشبكة بمتغير نسخة instance variable اسمه rows، بينما سنُخزِّن عدد الأعمدة بمتغير النسخة columns. يستخدم البرنامج تابع نسخةٍ تعاودي recursive instance method اسمه getBlobSize(r,c) لعدّ عدد المربعات بكائن، حيث يستطيع التابع الاستدلال على الكائن المطلوب الذي عدّ عدد مربعاته من خلال المعاملين r وc؛ أي عليه أن يَعُدّ عدد مربعات الكائن المُتضمِن للمربع الواقع بالصف r والعمود c، وإذا كان المربع بالموضِع (r,c) فارغًا، فستكون الإجابة ببساطة صفرًا؛ أما إذا لم يَكْن كذلك، فينبغي للتابع getBlobSize() أن يَعُدّ جميع المربعات المملوءة المُمكن الوصول إليها من المربع الموجود بالموضِع (r,c). تتلخَّص الفكرة باستدعاء getBlobSize() استدعاءً تعاوديًا لحساب عدد المربعات المملوءة المُمكن الوصول إليها من المواضع المجاورة، أي (r+1,c) و(r-1,c) و(r,c+1) و(r,c-1). بحساب حاصل مجموع تلك الأعداد، ثم زيادتها بمقدار الواحد لعدّ المربع بالموضِع (r,c) نفسه، نكون قد حصلنا على العدد الكلي للمربعات المملوءة المُمكِن الوصول إليها من الموضع (r,c). تعرض الشيفرة التالية تنفيذًا لتلك الخوارزمية، ولكنها تعاني من عيبٍ خطر؛ فهي ببساطة تؤدي إلى حدوث تعاودٍ لا نهائي infinite recursion. int getBlobSize(int r, int c) { // BUGGY, INCORRECT VERSION!! // 1 if (r < 0 || r >= rows || c < 0 || c >= columns) { // هذا الموضع غير موجودٍ بالشبكة، أي ليس هنالك أي كائنٍ بذلك الموضع // أعد كائنًا حجمه يساوي صفر return 0; } if (filled[r][c] == false) { // المربع ليس جزءًا من الكائن، لذلك أعد القيمة صفر return 0; } // 2 int size = 1; size += getBlobSize(r-1,c); size += getBlobSize(r+1,c); size += getBlobSize(r,c-1); size += getBlobSize(r,c+1); return size; } // end INCORRECT getBlobSize() [1] لاحِظ أن هذه الطريقة غير صحيحة، حيث تحاول عَدّ كل المربعات المملوءة التي يُمكِن الوصول إليها من الموضع (r,c). [2] عَدّ المربع بذلك الموضع، ثم عَدّ عدد الكائنات المتصلة بذلك المربع ارتباطًا أفقيًا أو رأسيًا لسوء الحظ، سيَعُدّ البرنامج بالأعلى نفس المربع أكثر من مرة، فإذا تضمّن الكائن مربعين على الأقل، فسيحاول البرنامج عدّ كل مربعٍ منهما بصورةٍ لانهائية. لنتخيل أننا نقف بالموِضِع (r,c) ونحاول أن نتبّع التعليمات، حيث تخبرنا التعليمة الأولى بأنه علينا التحرك للأعلى بمقدار صفٍ واحدٍ، ثم نُطبِق نفس الإجراء على ذلك المربع. بينما نُنفِّذ ذلك الإجراء، سيتعيّن علينا أن نتحرك لأسفل بمقدار صفٍ واحد، ونُطبِق نفس الإجراء مرةً أخرى، ولكن سيُعيدنا ذلك إلى الموضع (r,c) مجددًا، حيث سيتعين علينا التحرك لأعلى مجددًا، وهكذا. يُمكِننا أن نرى بوضوحٍ أننا سنستمر بذلك إلى الأبد، لذلك علينا أن نتأكَّد من أننا نُعالِج كل مربعٍ ونَعُدّه مرةً واحدةً فقط حتى لا ينتهي بنا الحال جيئةً وذهابًا. يَكْمُن الحل بأن نترك أثرًا من القيم المنطقية boolean مثل علامةٍ لتمييز المربعات التي زرناها فعليًا. بمجرد وضع تلك العلامة على مربعٍ معين، فلن نُعالجه مرةً أخرى، وسيقل بذلك عدد المربعات المتبقية غير المُعالَجة ونكون قد أحرزنا تقدمًا بتقليل حجم المشكلة، وعليه نتجنَّب حدوث تعاودٍ لا نهائي. سنُعرِّف مصفوفةً أخرى من القيم المنطقية visited[r][c] لتمييز المربعات التي زارها البرنامج وعالجها بالفعل، حيث أنه من الضروري بالطبع ضَبْط قيم جميع عناصر تلك المصفوفة إلى القيمة المنطقية false قبل استدعاء getBlobSize(). عندما يواجه التابع getBlobSize() مربعًا لم يزره من قبل، فسيَضبُط القيمة المقابلة لذلك المربع بالمصفوفة visited إلى القيمة المنطقية true؛ وفي المقابل، عندما يواجه التابع getBlobSize() مربعًا زاره من قبل، فعليه ببساطةٍ تخطيه دون إجراء أي معالجةٍ أخرى. في الحقيقة، يَكثُر استخدام ذلك الأسلوب من تمييز العناصر المُعالَجَة من غير المُعالجة بالخوارزميات التعاودية recursive algorithms. اُنظُر النسخة المُعدَّلة من التابع getBlobSize(). int getBlobSize(int r, int c) { if (r < 0 || r >= rows || c < 0 || c >= columns) { // هذا الموضع غير موجود بالشبكة، أي ليس هنالك أي كائنٍ بذلك الموضع // أعد كائنًا حجمه يساوي صفر return 0; } if (filled[r][c] == false || visited[r][c] == true) { // المربع ليس جزءًا من الكائن أو عُدّ من قبل، لذلك أعِد صفرًا return 0; } visited[r][c] = true; // 1 int size = 1; // 2 size += getBlobSize(r-1,c); size += getBlobSize(r+1,c); size += getBlobSize(r,c-1); size += getBlobSize(r,c+1); return size; } // end getBlobSize() [1] ضع علامةً تُبيِّن أن البرنامج زار هذا الموضع حتى لا نَعُدّه مرةً أخرى أثناء الاستدعاءات التعاودية. [2] عدّ المربع بذلك الموضع، ثم عدّ عدد الكائنات المتصلة بذلك المربع ارتباطًا أفقيًا أو رأسيًا. يَستخدِم البرنامج التابع المُعرَّف أعلاه لتحديد حجم كائنٍ معين عندما ينقُر المُستخدِم على مربعٍ ينتمي لذلك الكائن. بعد انتهاء التابع getBlobSize() من مهمته، ستكون المصفوفة visited مضبوطةً بحيث تُشير إلى جميع مربعات الكائن. بناءً على ذلك، سيُظهِر التابع المسؤول عن رسم الشبكة المربعات التي قد زارها باللون الأحمر، وعليه سيُصبِح الكائن مرئيًا. يُستخدَم التابع getBlobSize() أيضًا لعدّ عدد الكائنات، كما هو موضحٌ في الشيفرة التالية. void countBlobs() { int count = 0; // عدد الكائنات // 1 for (int r = 0; r < rows; r++) for (int c = 0; c < columns; c++) visited[r][c] = false; // 2 for (int r = 0; r < rows; r++) for (int c = 0; c < columns; c++) { if (getBlobSize(r,c) > 0) count++; } draw(); // 3 message.setText("The number of blobs is " + count); } // end countBlobs() [1] أولًا، امسح المصفوفة visited. سيحدِّد التابع getBlobSize() كل مربعٍ مملوءٍ مر عليه من خلال ضبط عنصر المصفوفة المقابل إلى القيمة المنطقية true. وبمجرد زيارة مربعٍ معين ووضع علامةٍ عليه، فسيبقى كذلك إلى أن ينتهي التابع من عدّ كل الكائنات، وسيمنع هذا عدّ نفس الكائن أكثر من مرة. [2] استدعِ التابع getBlobSize() لكل موضعٍ في الشبكة من أجل حساب حجم الكائن الموجود بذلك الموضع؛ فإذا كان حجمه لا يُساوي الصفر، فزِد قيمة العداد بمقدار الواحد. لاحِظ أنه في حالة عُدنا إلى موضعٍ ينتمي لكائنٍ زرناه من قبل، فسيعيد التابع getBlobSize() القيمة صفر، وبذلك لن نَعُدّ ذلك الكائن مرةً أخرى. [3] أعِد رسم شبكة المربعات. لاحِظ أن كل المربعات المملوءة ستكون باللون الأحمر. ترجمة -بتصرّف- للقسم Section 1: Recursion من فصل Chapter 9: Linked Data Structures and Recursion من كتاب Introduction to Programming Using Java. اقرأ أيضًا كيفية كتابة برامج صحيحة باستخدام لغة جافا تطبيق عملي: بناء لعبة ورق في جافا التعاود recursion والمكدس stack في جافاسكربت1 نقطة
-
من السهل جدًّا تصميم خط منقّط باستخدام الفوتوشوب. كل ما تحتاج إليه هو تتبّع هذه الخطوات الثلاثة. 1. كيف تجهّز إعدادات أداة القلم لتصميم تأثير الخط المنقّط؟ افتح الصورة التي تريد رسم تأثير الخط المنقط حولها. أنا اخترت صورة هذه الكعكة. الآن اختر أداة القلم Pen Tool مع اختيار خيار الشكل Shape من شريط خيارات هذه الأداة عبر القائمة المنسدلة. سنتابع تجهيز إعدادات القلم من شريط الخيارات العلوي. اجعل لون التعبئة Fill بدون لون واجعل لون الحدود باللون الذي تريده. أنا اخترت اللون الأبيض وجعلتُ حجم الحدود 0.65pt. 2. كيف نستخدم أداة القلم لرسم مسار تحديد قبل تأثير الخط المنقّط؟ إذا انتهيت من الخطوة الأولى، عليك أن تقوم برسم تحديد حول الصورة. باستخدام أداة القلم كما يلي. 3. كيف تُجهّز وتُعِد تأثير الخط المنقّط النهائي؟ وصلنا إلى الخطوة الأخيرة. استخدم أداة القلم مع التأكيد على أن الخط الذي رسمناه محدّد سلفًا ثم اختر خطًّا منقطًّا من شريط الخيارات العلوي من قائمة Stroke Option. يمكنك تغيير إعدادات شكل وحجم الخطوط المنقطة من زر More Option أسفل القائمة. أنا قمتُ بجعل حجم الخط 4 وحجم الفجوة بين الخطوط 2 من أجل هذا التصميم. وبهذا يتم صناعة خط منقط حول الصور في الفوتوشوب. وهذه هي النتيجة النهائية. ترجمة -وبتصرّف- للمقال: How to Make Dashed Line Effect in Photoshop لصاحبه: Bijutoha1 نقطة












.png.11911b857e50dab3d04d1da344d193b2.png)
