عناوين IP ما هي إلا سلسلة مكونة من 32 رقمًا ثنائيًا؛ وسنستعرض في هذا الدرس مراجعةً عن نظام العد الثنائي لكي نفهم عملها. وسنبدأ بمقارنته بالنظام العشري، وسنشرح كيف أنَّ الرقم 2 هو اللبنة الأساسية لعملية العد؛ وسنمنحك الفرصة في هذا الدرس للتدرب على التحويل من عددٍ بالنظام العشري إلى رقمٍ عددٍ الثنائي وبالعكس.
الأعداد بالنظام العشري والنظام الثنائي
لما كانت الأعداد بالنظام الثنائي مهمةً جدًا في عناوين IP والشبكات الفرعية (subnets)، فلنلقِ نظرةً أعمق على بنيتهم وقيمهم؛ وسنحتاج أيضًا إلى أن نتعلم كيفية تحويلهم إلى أعدادٍ بالنظام العشري لأننا -نحن البشر- لسنا «أذكياء» كفايةً للتعامل مع الأعداد بالنظام الثنائي، ونرغب في التعامل مع أشياءٍ ألفنا استعمالها (مثل الأرقام بالنظام العشري)؛ وفي الواقع، أفضل طريقة لفهم الأعداد الثنائية هي مقارنتها بالأعداد العشرية؛ فالسؤال الفلسفي الأول لهذا اليوم هو: ما هي الأعداد العشرية؟ نحن نعرفها ﻷننا نتعامل معها يوميًا؛ فأساسها (base) هو الرقم 10، والأعداد العشرية ما هي إلا سلسلة من الأرقام التي تتراوح بين 0 و 9؛ ونعلم أنَّ خانة أو منزلة الرقم في الأعداد العشرية تُفسِّر دلالة ذاك الرقم؛ أي بكلامٍ آخر، نحن نعلم معنى أول رقم في أول خانة في العدد؛ ونعلم أنَّ قيمة العدد هي الرقم نفسه إن كان أقل من 10؛ ونعلم أن الخانة الثانية هي العشرات، والقيمة الفعلية هي قيمة الرقم مضروبًا بالرقم 10، وبنفس الطريقة نعرف أنَّ الخانة الثالثة هي المئات، والرابعة هي الآلاف، والخامسة هي عشرات الآلاف، وهلمَّ جرًّا. وهذه العشرات والمئات والآلات ما هي إلا قوى الرقم 10.
|
عشري |
ثنائي |
عشري |
ثنائي |
|---|---|---|---|
|
0 |
0000 |
9 |
1001 |
|
1 |
0001 |
10 |
1010 |
|
2 |
0010 |
11 |
1011 |
|
3 |
0011 |
12 |
1100 |
|
4 |
0100 |
13 |
1101 |
|
5 |
0101 |
14 |
1110 |
|
6 |
0110 |
15 |
1111 |
|
7 |
0111 |
16 |
10000 |
|
8 |
1000 |
17 |
10001 |
حسنًا، الأعداد الثنائية شبيهة جدًا بالأعداد العشرية، لكن الأساس هو 2، لذا نتمكن من استعمال الرقمين 0 و 1 فقط؛ وهذان الرقمان يُستعمَلان من الحواسيب لأنه يسهل التعامل معهم؛ إذ نستطيع أن نبني حواسيب تستعمل الأعداد ذات الأساس 10، لكنها ستكون باهظة الثمن للغاية.
تتبع الأعداد الثنائية نفس الآلية أو العملية المستعملة لبناء الأعداد العشرية؛ إذ أنَّ العدد الثنائي هو سلسلةٌ من الأرقام، ويجب أن يكون كل رقم من تلك الأرقام إما 0 أو 1 وتلعب خانة (أو مكان) الرقم دورًا في تحديد قيمة العدد؛ فجميع الخانات تمثِّل قوى للأساس، وفي هذه الحالة أساس العد الثنائي هو الرقم 2؛ أي أنَّ الخانات تمثِّل قوة (Exponentiation) الرقم 2.
لمحة نظرية عن التحويل من النظام العشري إلى الثنائي
قد تستعجب من معرفة قيمة عدد ثنائي بسرعة بمجرد النظر إليه؛ حسنًا، سأخبرك أنَّ الأمر منوطٌ باعتيادك على قراءة الأعداد الثنائية. إذ نألف الأعداد العشرية ونعرف كيف نحسب القيمة الإجمالية للعدد، أو على الأقل تقديرها أو أن يكون لدينا فكرة عن الناتج. فيمكننا النظر إلى عددٍ ما ونرى أنَّ أول خانة هي الرقم 9، والخانة الثانية ستكون من العشرات وهي الرقم 2، التي تمثِّل القيمة 20؛ أما الخانة الثالثة فهي الرقم 8 وتمثِّل المئات، وتعني 800 وهكذا. ربما لا نفكِّر في الأمر كثيرًا عند قراءتنا للأعداد العشرية، لكن كل قيمة مرتبطة بمنزلة أو خانة ما هي إلا قوى الرقم 10.
مثال عن تفسير عدد ذي الأساس 10 – العدد: 63204829
|
الرقم الأقل أهميةً |
|
|
|
|
|
|
الرقم الأكثر أهميةً |
|
|---|---|---|---|---|---|---|---|---|
|
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
الأساس الأس |
|
9 |
2 |
8 |
4 |
0 |
2 |
3 |
6 |
قيمة الخانة |
|
1 |
10 |
100 |
1000 |
10000 |
100000 |
1000000 |
10000000 |
المنزلة العشرية |
|
9 |
20 |
800 |
4000 |
0 |
200000 |
3000000 |
60000000 |
القيمة النهائية للخانة |
60000000 + 3000000 + 200000 + 0 + 4000 + 800 + 20 + 9 = 63204829
كما ذكرنا سابقًا، الأمر متعلقٌ باعتيادك على إجراء عملية الحساب. فالتحويل الثنائي، أو حساب قيمة العدد الثنائي، هي نفس العملية تمامًا؛ لكن لدينا هنا أرقامٌ تحتوي 0 و 1، ثم سنطبِّق عليها نفس المبادئ التي تقول أن كل رقم يجب أن يُضرَب بقوى 2 لأن الأساس في الأعداد الثنائية هو2، فأول رقم (1) سيُضرَب بالرقم 1، أي 2 للقوة 0؛ أما الرقم الثاني (0) سيُضرَب بالرقم 2، الذي هو 2 للقوة 1؛ أما ثالث خانة فستُضرَب بالرقم 2 للقوة 2 (مربَّع)، والخانة الرابعة بالرقم 2 للقوة 3 (مُكعَّب) وهكذا. وعليك أن تعتبر أنَّ آخر بت في العدد هو أهم بت، مثَلُهُ كمَثَلِ الأعداد العشرية.
مثال عن تفسير عدد ذي الأساس 2 – العدد: 1110100 (223)
|
الرقم الأقل أهميةً |
|
|
|
|
|
|
الرقم الأكثر أهميةً |
|
|---|---|---|---|---|---|---|---|---|
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
الأساس الأس |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
قيمة الخانة |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
القيمة العشرية |
|
1 |
0 |
0 |
8 |
0 |
32 |
64 |
128 |
القيمة النهائية للخانة |
128 + 64 + 32 + 0 + 8 + 0 + 0 + 1 = 233
تبدأ مضاعفات العدد 2 من أقل البتات منزلةً ومن منزلة أو خانة الرقم الذي يمثِّل الأس للأساس 2 الذي علينا ضرب الرقم به بدءًا من الصفر؛ فعندنا 8 خانات في المثال السابق، الذي يتكون من 8 بتات التي تمثِّل بايتًا، تذكر أننا نُجمِّع البتات والبايتات، ونفصلها بنقط كي نحصل على عناوين IP. قيمة العدد الثنائي السابق هي 223 بالنظام العشري.
قوى الرقم 2
لقد تقلصت مشكلتنا الأساسية -التي هي النظر إلى العدد الثنائي وحساب قيمته العشرية بسرعة لكي نستطيع فهم عناوين IP بالنظر إليها- إلى معرفة قوى الرقم 2، لأننا نعرف أن الخانة أو مكان الرقم مهم ويعطينا قوى الرقم 2 التي سنستخدمها في حساباتنا. فلنعد إلى مثالنا السابق عن البايت (أو 8 بت)، فكل ما علينا تذكره هو ثماني قيم: أول قوى الرقم 2 هي 2 للقوة 0 وتساوي 1، و2 للقوة 1 هي 2، و2 مربع هي 4، وهلمَّ جرًا حتى يحصل على كل تلك القيم؛ فكر بها مليًّا، حفظها ليس صعبًا، 1، 2، 4، 8، 16، 32، 64، 128:
-
قوى الرقم 2
العملية الحسابية
القيمة
20
1 21
2
2
22
2 * 2
4
23
2 * 2 * 2
8
24
2 * 2 * 2 * 2
16
25
2 * 2 * 2 * 2 * 2
32
26
2 * 2 * 2 * 2 * 2 * 2
64
27
2 * 2 * 2 * 2 * 2 * 2 * 2
128
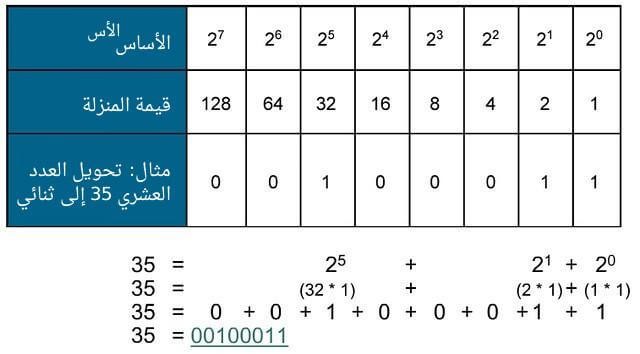
مثال عن التحويل من عدد عشري إلى ثنائي
من المفيد أحيانًا في عناوين IP التحويل من الأعداد العشرية إلى الأعداد الثنائية؛ وخصيصًا في الشبكات الفرعية، التي سنبحث أمرها في الدرس القادم. هذه طريقة التحويل: نحن نعلم أن القيمة العشرية ستكون سلسلة أرقامٍ ثنائية في العدد الثنائي، وكل رقم من تلك الأرقام سيكون له قيمة عشرية معيّنة بناءً على منزلته أو خانته. فمثلًا، الرقم 1 في الخانة السابعة (لاحظ أن الخانة السابعة رقمها 8، ﻷننا نعد من 0 إلى 7) يُمثِّل الرقم العشري 128؛ والرقم 1 في الخانة الثالثة (نذكر مرة أخرى أننا نعد من 0 إلى 7) يُمثِّل الرقم 8؛ فبعد أن نضع في بالنا قوى الرقم 2، كل ما علينا فعله (للتحويل بين العشري إلى الثنائي) هو العثور على أكبر قوى 2 التي تكون أصغر من العدد العشري الذي نريد تحويله، ثم نضع في تلك المنزلة الرقم الثنائي 1 ثم نطرح العدد الناتج من العدد العشري الأصلي.
ثم نكرر العملية حتى تصبح نتيجة عمليات لطرح مساويةً للرقم 0؛ لنلقِ نظرةً على هذا المثال، لنقل أننا نريد تحويل العدد 35 إلى النظام الثنائي، فلنفكر ما هي أكبر قوة للرقم 2 أصغر من (أو تتسع في) 35؟ الجواب بدهي، إنها 32، إذ لا تتسع 128 و 64 في العدد العشري المُحوَّل (35)، ولهذا تكون قيمة تلك المنزلتين الثنائية مساويةً للصفر (0)، أي أنَّ أول 1 هو 32، فنضع 1 في تلك المنزلة (أو الخانة) ثم نطرح 32 من 35، والناتج هو 3؛ لنكرر الآن العملية: ما هي أكبر قوة للرقم 2 تتسع في 3؟ لا تتسع 16 أو 8 أو 4، إذ أنها جميعًا أكبر من 3، وسنضع أصفارًا في خاناتها؛ فالرقم الذي يتسع في 3 هو 2 للقوة (أو للأس) 1، أي 2؛ ونضع الرقم الثنائي 1 في تلك المنزلة ونطرح 2؛ حيث 3 ناقص 2 يساوي 1، الذي يساوي إلى 2 للقوة 0، ونضع الرقم الثنائي 1 في تلك المنزلة ونطرح 1، والجواب النهائي هو 0؛ وبهذا يكتمل التحويل ويكون ناتج تحويل العدد العشري 35 إلى ثنائي هو 00100011.
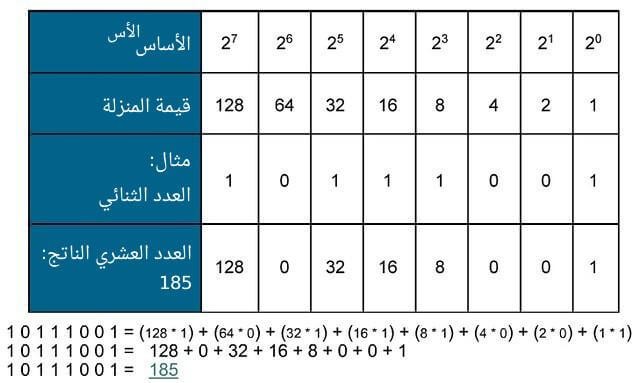
مثال عن التحويل من عدد ثنائي إلى عشري
التحويلات من الأعداد الثنائية إلى الأعداد العشرية أكثر سهولةً، فكل ما علينا فعله هو تطبيق نفس العملية التي قادتنا إلى فهم الأعداد الثنائية كما يلي: نأخذ الأرقام في العدد الثنائي ونضربها بقوة العدد 2 الموافقة للخانة بدءًا من الخانة 0 في أقصى اليمين (التي هي «الرقم الأقل أهميةً») منتقلين إلى اليسار حتى نصل إلى الخانة السابعة (التي هي «الرقم الأكثر أهميةً»)، ثم سنجمع الأرقام الناتجة معنا لنحصل على القيمة العشرية له.
الرقم 1 في الخانة 0 يعني أنَّ علينا ضرب الرقم 1 بقوة الرقم 2 الموافقة للخانة، التي هي 1 أيضًا؛ أما الرقم 0 فيعني أن نضرب 0 بقوة العدد 2، ولهذا لن تُضاف أيّة قيمة للنتيجة النهائية؛ وكذلك الأمر بالنسبة إلى الخانة التي تليها؛ أما الخانة الرابعة ففيها الرقم 1، فسيضرب الرقم 1 بقوة الرقم 2 الملائمة للمنزلة (تذكر أنَّ ترتيب الخانة الرابعة هو 3 لأننا نبدأ العد من الصفر) التي هي 2 للقوة 3 ثم سنضيفها للناتج؛ وبإكمال تلك العملية حتى نصل إلى آخر خانة، ويصبح لدينا سلسلة من الأرقام العشرية التي عندما نجمعها مع بعضها فسنحصل على الناتج بالنظام العشري، الذي هو 185.
ترجمة -وبتصرّف- للمقال Understanding Binary Basics.













أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.