كشف الأخطاء على مستوى البت في الشبكات الحاسوبية

تُدخَل أحيانًا أخطاء البت في الإطارات، ويحدث هذا على سبيل المثال بسبب التداخل الكهربائي (electrical interference) أو التّشويش الحراري (thermal noise)، وعلى الرّغم من ندرة الأخطاء خاصًّة على الروابط الضوئيّة، إلا أنّ هناك حاجة إلى بعض الآليات لاكتشاف هذه الأخطاء، وذلك من أجل اتخاذ الإجراءات الصحيحة، بينما يُترك المستخدم النهائي بخلاف ذلك يتساءل عن سبب ظهور خطأ صياغي (syntax error) فجأةً في برنامج مكتوب بلغة C يكون قد صُرِّف بنجاح منذ لحظة واحدة فقط، رغم أنّ كلّ ما حدث في غضون ذلك هو نسخه عبر نظام ملفّات الشبكة.

هناك تاريخ طويل من تقنيّات التعامل مع أخطاء البت في أنظمة الحاسوب، حيث يعود تاريخه إلى الأربعينات على الأقل، وتُعَد شيفرات هامينغ (Hamming) وريد-سولومون (Reed-Solomon) مثالين بارزين طُوِّرا للاستخدام في قارئات البطاقات المُثقَّبة (punch card readers) عند تخزين البيانات على أقراص مغناطيسيّة (magnetic disks) وفي الذواكر الأساسيّة القديمة، حيث يشرح هذا القسم بعض تقنيّات اكتشاف الأخطاء الأكثر استخدامًا في الشبكات.

يُعدّ اكتشاف الأخطاء جزءًا من المشكلة فقط، والجزء الآخر هو تصحيح الأخطاء بمجرد اكتشافها، ويمكن اتّباع طريقتين أساسيّتين عندما يكتشف مستلم الرسالة خطأً، والطريقة الأولى هي إبلاغ المرسل بأن الرسالة تالفة حتّى يتمكّن المرسل من إعادة إرسال نسخة من الرسالة، وبالتالي إذا كانت أخطاء البت ناذرة، فمن المحتمل أن تكون النسخة المعاد إرسالها خاليةً من الأخطاء؛ أمّا الطريقة الثانية، فتتمثّل في سماح بعض أنواع خوارزميّات اكتشاف الأخطاء للمستلم بإعادة بناء الرسالة الصحيحة حتّى بعد تلفها، حيث تعتمد مثل هذه الخوارزميات على شيفرات تصحيح الأخطاء (error-correcting codes) الموضّحة أدناه. وواحدة من أكثر التقنيّات شيوعًا لاكتشاف أخطاء الإرسال هي تقنيّة تُعرف باسم فحص التّكرار الدوري (cyclic redundancy check ويختصر إلى CRC)، والتي تُستخدم في جميع بروتوكولات مستوى الربط التي ستناقَش في هذا المقال تقريبًا، حيث سيوضّح هذا القسم خوارزميّة CRC الأساسيّة، ولكنّه سيشرح أوّلًا مخطّط المجموع الاختباري (checksum) الأبسط الذي تستخدمه العديد من بروتوكولات الإنترنت.

الفكرة الأساسيّة وراء أيّ مخطّط اكتشاف أخطاء هي إضافة معلومات زائدة إلى إطار، بحيث يمكن استخدامها لتحديد فيما إذا كانت الأخطاء قد أُدخلت أم لا، ويمكنك تخيّل إرسال نسختين كاملتين من البيانات في أسوأ الأحوال، فإذا كانت النسختان متطابقتين في المستقبل، فمن المحتمل أن تكون كلتا النسختين صحيحتين، وإذا اختلفتا، فقد أُدخِل خطأٌ في إحدى النسختين (أو كلتيهما) وبالتالي يجب إهمالها، لكن هذا يُعدّ مخطّطًا سيّئًا إلى حدّ ما لاكتشاف الأخطاء وذلك لسببين، أوّلهما إرسال هذا المخطّط n بت زائدة (redundant) لرسالة بحجم n بت، وثانيهما عدم اكتشاف العديد من الأخطاء مثل أيّ خطأٍ يحدث لإتلاف مواضع البت نفسها في النسختين الأولى والثانية من الرسالة، ولكن هدف شيفرات اكتشاف الأخطاء هو توفير احتمال كبير لاكتشاف الأخطاء مع عدد قليل نسبيًّا من البتّات الزائدة (redundant bits)، ولحسن الحظ يمكن القيام بأفضل بكثير من هذا المخطط البسيط، حيث يمكن توفير قدرة قويّة جدًّا لاكتشاف الأخطاء مع إرسال k بتّ زائدة فقط لرسالة بحجم n بت، حيث k أصغر بكثير من n، ففي شبكة إيثرنت على سبيل المثال لا يتطلّب الإطار الذي يحمل ما يصل إلى 12000 بتًّا (1500 بايت) من البيانات سوى شيفرة CRC مؤلّفة من 32 بتًا، أو كما يُعبَّرعنها CRC-32، حيث ستلتقط مثل هذه الشيفرة الغالبيّة العظمى من الأخطاء كما سترى لاحقًا.

يمكننا القول أنّ البتات الإضافية التي نرسلها زائدةٌ نظرًا لعدم إضافتها لمعلومات جديدة إلى الرسالة، بل تُشتَق مباشرةً من الرسالة الأصليّة باستخدام خوارزميّة معروفة جيّدًا، بحيث يعرف كلّ من المرسل والمستقبل بالضّبط ما هي هذه الخوارزميّة. ويطبّق المرسل الخوارزميّة على الرسالة لتوليد تلك البتات الزائدة، ثم ينقل الرسالة وتلك الأجزاء الإضافية القليلة. وإذا طبّق المستقبل نفس الخوارزميّة على الرسالة المستلمة، فيجب إنتاج نفس نتيجة المرسل (في حالة عدم وجود أخطاء)، حيث يوازن المستقبل تلك النّتيجة مع النّتيجة التي أرسلها المرسل إليه، فإذا تطابقت، يمكنه استنتاج (مع احتمال كبير) عدم حدوث إدخال أخطاءٍ في الرسالة أثناء الإرسال، وإذا لم تتطابق يمكن التأكّد من تلف الرسالة أو البتّات الزائدة، مع وجوب اتّخاذ الإجراء المناسب، أي إهمال الرسالة أو تصحيحها إذا كان ذلك ممكنًا.

توجد ملاحظةٌ واحدة حول المصطلحات الخاصّة بهذه البتات الإضافيّة، حيث يشار إليها باسم شيفرات اكتشاف الأخطاء، وقد يطلق عليها في حالات محدّدة، عندما تعتمد الخوارزميّة على الجمع (addition) لإنشاء الشيفرة مثلًا، اسم المجموع الاختباري (checksum)، حيث سترى أنّ المجموع الاختباري للإنترنت قد سُمي بطريقة مناسبة، فهو فحص خطأ يستخدم خوارزميّة جمع، ولكن لسوء الحظ تُستخدَم غالبًا كلمة المجموع الاختباري بصورة غير دقيقة للإشارة إلى أي نوع من أنواع شيفرة اكتشاف الأخطاء بما في ذلك شيفرات CRC، وبالتالي قد يكون هذا محيّرًا، لذلك يمكنك استخدام المجموع الاختباري للتطبيق على الشيفرات التي تستخدم الجمع بالفعل، ويمكنك استخدام شيفرة اكتشاف الأخطاء للإشارة إلى صنف الشيفرات العامّة الموضّحة في هذا القسم.

خوارزمية مجموع الإنترنت الاختباري (Internet Checksum Algorithm)

تتمثل الطّريقة الأولى لاكتشاف الأخطاء في مجموع الإنترنت الاختباري، وعلى الرّغم من عدم استخدامه على مستوى الرابط، إلا أنّه يوفّر نفس نوع وظائف آليّة CRC. وتُعدّ الفكرة الكامنة وراء مجموع الإنترنت الاختباري بسيطةً للغاية، حيث تضاف كلّ الكلمات المرسَلة ثمّ ترسَل نتيجة هذا المجموع، والنتيجة هي المجموع الاختباري، حيث يجري المستقبل نفس العمليّات الحسابيّة على البيانات المستلَمة ويوازن النتيجة مع المجموع الاختباري المستلَم، وفي حالة تلف أي بيانات مرسلَة، بما في ذلك المجموع الاختباري نفسه، فلن تتطابق النتائج، لذلك يعلم المستقبل بحدوث خطأ.

يمكنك تخيّل العديد من الاختلافات حول فكرة المجموع الاختباري الأساسيّة، ويعمل المخطط الذي تستخدمه بروتوكولات الإنترنت على النحو التالي: افترض أنّ البيانات التي سيطبّق عليها المجموع الاختباري هي سلسلة من الأعداد الصحيحة المؤلفة من 16 بتًا، ثم اجمعهم معًا باستخدام متمّم الواحد (ones’ complement) ذو 16 بت (الموضح أدناه)، ثم خذ متمّم الواحد للنتيجة، فهذا الرقم المؤلّف من 16 بتًا هو المجموع الاختباري، حيث يُمثَّل العدد الصحيح السالب -x باستخدام متمّم الواحد كمتمم للعدد x، أي يُقلَب كل بت من x، ويجب إضافة حِمل من البت الأكثر أهميّةً إلى النتيجة عند جمع الأعداد باستخدام مُتمّم الواحد. افترض على سبيل المثال جمع العددين -5 و -3 باستخدام مُتمّم الواحد على أعداد صحيحة مؤلّفة من 4 بتات: +5هي 0101 لذا -5 هي 1010، و +3 هي 0011 لذا -3 يساوي 1100. إذا جمعت العددين 1010، و1100، مع تجاهل الحمل، ستحصل على 0110. لكن بسبب حقيقة أنّ هذه العمليّة تسببت في حمل من البت الأكثر أهميّة باستخدام متمّم الواحد لذلك يجب زيادة النتيجة، قتصبح 0111، وهو تمثيل متمّم الواحد للعدد -8 الذي تحصل عليه من خلال قلب بتات العدد 1000.

تعطي الشيفرة الآتية تطبيقًا مباشرًا لخوارزمية مجموع الإنترنت الاختباري، ويعطي الوسيط count طول المتغيّر buf المُقاس بطول 16 بت، حيث تفترض الشيفرة أنّ المتغيّر buf محشوٌّ أصفارًا إلى حد 16 بت:

u_short
cksum(u_short *buf, int count)
{
    register u_long sum = 0;

    while (count--)
    {
            sum += *buf++;
            if (sum & 0xFFFF0000)
            {
                    /* ظهر حِمل في البت الأعلى أهميةً، لذلك أضف واحدًا إلى المجموع */
                    sum &= 0xFFFF;
                    sum++;
            }
    }
    return ~(sum & 0xFFFF);
}

تضمن الشيفرة السابقة استخدام العمليّة الحسابيّة لمتمّم الواحد بدلًا من المتمّم الثنائي المستخدم في معظم الأجهزة، ويمكنك ملاحظة استخدام عبارة if داخل حلقة while، وإذا وُجِد حِمل في البت الأعلى من 16 بت في المتغيّر sum الذي يُمثّل المجموع، فيجب زيادة المجموع كما في المثال المذكور سابقًا، وتحقق خوارزمية المجموع الاختباري نتائجًا جيّدةً عند استخدام عددٍ قليل من البتّات الزائدة، 16 بتًا فقط لأية رسالةٍ ذات أيّ طول، ولكنها لا تحقق نتائجًا جيدة للغاية بالنسبة لاكتشاف الأخطاء الأقوى، إذ لن يُكتشَف على سبيل المثال زوجٌ من الأخطاء أحاديّة البت، أحدهما يزيد كلمةً والآخر ينقص كلمةً أخرى بنفس المقدار، ويعود سبب استخدام مثل هذه الخوارزميّة رغم كون حمايتها ضعيفةً نسبيًّا ضدّ الأخطاء (مقارنةً بخوارزميّة CRC على سبيل المثال)، هو أنها خوارزميّة بسيطة، فهذه الخوارزميّة تُعدّ أسهل بكثير في التطبيق ضمن البرمجيّات، وقد أشارت التجربة إلى أنّ المجموع الاختباري (checksum) لهذا النموذج مناسب، ولكن أحد أسباب عدّه مناسبًا يعود لكون المجموع الاختباري بمثابة خطّ الدفاع الأخير في بروتوكول نقطة لنقطة، حيث تلتقط خوارزميّاتٍ أقوى لاكتشاف الأخطاء، مثل خوارزمية CRC، باكتشافها لغالبيّة الأخطاء على مستوى الروابط.

فحص التكرار الدوري (Cyclic Redundancy Check أو اختصارًا CRC)

يجب أن يكون واضحًا الآن أن الهدف الرئيسي في تصميم خوارزميات اكتشاف الأخطاء هو تكبير احتمالية اكتشاف الأخطاء إلى الحدّ الأقصى باستخدام عدد صغير فقط من البتّات الزائدة، حيث تُستخدم خوارزميّة فحص التكرار الدوري بعض الحسابات القويّة إلى حدّ ما لتحقيق هذا الهدف، وتوفّر خوارزميّة CRC ذات 32 بتًا على سبيل المثال حمايةً قويّةً ضدّ أخطاء البت الشائعة الموجودة في الرسائل التي يبلغ طولها آلاف البايتات. الأساس النظري لهذه الخوارزمية مُتجذّر في فرعٍ من فروع الرياضيات يسمّى الحقول المحدودة (finite fields). قد يبدو هذا صعبًا، ولكن يمكن فهم الأفكار الأساسيّة بسهولة، ابدأ بافتراض أن رسالةً مؤلّفةً من (n + 1) بت ممثّلةٌ بواسطة كثير حدود (polynomial) من الدّرجة n، أي كثير الحدود الذي حدّه الأعلى رتبةً هو xⁿ. تُمثَّل الرسالة بواسطة كثير حدود باستخدام قيمة كلّ بت في الرسالة كمعاملٍ لكلّ حدٍ من كثير الحدود، بدءًا من البت الأعلى أهميّةً لتمثيل الحدّ الأعلى رتبةً، حيث تتكوّن رسالةٌ مؤلّفة من 8 بتات، وهي البتات 10011010 على سبيل المثال التي تتوافق مع كثير الحدود التالي:

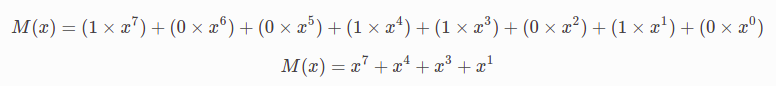
بالتالي يمكن التفكير في المرسل والمستقبل على أنهما يتبادلان كثيرات الحدود مع بعضهما البعض. يجب على المرسل والمستقبل الاتفاق على كثير الحدود القاسم (divisor polynomial) الذي يُرمز له C (x) لحساب CRC، حيث C (x) هو كثير حدود من الدرجة k. افترض أن C (x) = x³ + x² + 1 على سبيل المثال، حيث k = 3 في هذه الحالة؛ أمّا الإجابة على السؤال (من أين أتى كثير الحدود C (x)؟) هي (ابحث عنه في السلسلة)، فإن اختياره له تأثير كبير على أنواع الأخطاء التي يمكن اكتشافها بطريقة موثوقة. هناك عدد قليل من كثيرات الحدود القاسمة التي تُعد اختيارات جيدة جدًا لبيئات مختلفة، ويُضاف ذلك الاختيار الدقيق كجزءٍ من تصميم البروتوكول، كما يستخدم معيار إيثرنت على سبيل المثال كثير الحدود المعروف ذو الدرجة 32.

إذا أراد المرسل إرسال رسالة M (x) بطول n + 1 بت، فما يُرسَل بالفعل هو الرسالة التي طولها (n + 1) بت بالإضافة إلى k بت. وتدعى الرسالة المرسلة بالكامل بما في ذلك البتات الزائدة P (x). يجب جعل كثير الحدود الذي يمثّل P (x) قابلًا للقسمة تمامًا على C (x)، فإذا أُرسل P (x) عبر رابط دون حدوث أخطاء أثناء الإرسال، فيجب أن يكون المستقبل قادرًا على قسمة P (x)على C (x) تمامًا بلا باقٍ. ومن ناحية أخرى، إذا حدث خطأٌ ما في P (x) أثناء الإرسال، فلن يقبل كثير الحدود المستقبل القسمة تمامًا علىC (x)، وبالتالي سيحصل المستقبل على باقٍ غير صفريّ مما يعني حدوث خطأ.

سيساعدك فهم ما يلي إذا كنت تعرف القليل عن حساب كثيرات الحدود، فهو يختلف قليلًا عن حساب الأعداد الصحيحة العاديّة، حيث ستتعامل هنا مع صنفٍ خاصّ من حساب كثيرات الحدود، فقد تكون المعامِلات (coefficients) واحدًا أو صفرًا فقط، وتُجرى العمليّات على المعاملات باستخدام نظام الحساب modulo 2، الذي يُشار إليه باسم نظام حساب modulo 2 لكثير الحدود. لكن نظرًا لأن هذه السلسلة عن الشبكات، وليست عن الرياضيات، فيجب التركيز فقط على الخصائص الرئيسيّة لهذا النوع من الحساب (والتي نطلب منك قبولها بناءً على الثّقة):

يمكن تقسيم أيّ كثير حدود B (x) على كثير الحدود القاسم C (x) إذا كان B (x) من درجة أعلى من C (x).
يمكن تقسيم أيّ كثير حدود B (x) مرةً واحدة بواسطة كثير الحدود القاسم C (x) إذا كان B (x) من نفس درجة C (x).
ينتج باقي قسمة B (x) على C (x) من خلال إجراء عمليّة XOR على كلّ زوج من المعاملات المتطابقة.

يمكن قسمة كثير الحدود x³ + 1 مثلًا على كثير الحدود x³ + x² + 1 (لأنّ كليهما من الدرجة 3) والباقي هو ‎0×x³+1×x²+0×x¹+0×x⁰=x² (الذي نتج عن طريق إجراء عملية XOR على معاملات كل حد)، وبالتالي يمكن القول أنهّ يمكن قسمة 1001 على 1101 مع باقٍ هو 0100 (يجب أن تكون قادرًا الآن على رؤية أن الباقي هو مجرد تطبيق لعمليّة XOR ثنائيّة على الرسالتين)، وبعد أن عرفت القواعد الأساسيّة لتقسيم كثيرات الحدود، يمكنك إجراء قسمة طويلة، وهو أمر ضروري للتعامل مع الرسائل الأطول.

تذكر أنك تريد إنشاء كثير حدود للإرسال مشتق من الرسالة الأصلية M (x)، فهل k بت أطول من M (x)، وهل M (x) قابلة للقسمة تمامًا على C (x)؟ يمكنك القيام بذلك بالطريقة التالية:

اضرب M (x) بـ x^k وهذا يعني إضافة k صفرًا في نهاية الرسالة. ادعُ هذه الرسالة الصفرية الموسعة T (x).
اقسم T (x) على C (x) وجِد الباقي.
اطرح الباقي من T (x).

يجب أن يكون واضحًا أن ما تبقّى في هذه المرحلة هو رسالة قابلة للقسمة تمامًا على C (x)، وقد تلاحظ أيضًا أنّ الرسالة الناتجة تتكوّن من M (x) متبوعةً بالباقي الناتج عن الخطوة 2، فعند طرح الباقي (والذي لا يمكن أن يزيد طوله عن k بت)، فكأنّك أجريت عمليّة XOR فقط للباقي مع k صفرًا التي أُضيفت في الخطوة 1، وسيصبح هذا الجزء أوضح بمثال:

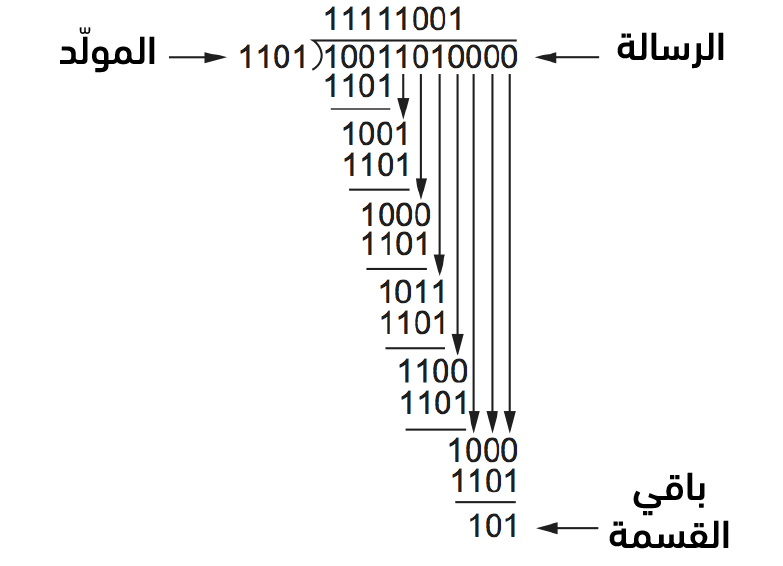
افترِض أنّ الرسالة هي x⁷ + x⁴ + x³ + x¹ أو 10011010. ابدأ بالضرب بـ x³، فكثير الحدود القاسم هو من الدرجة 3، وهذا يعطي 10011010000، ثمّ اقسم النتيجة السابقة على C (x) الذي يقابل 1101 في هذه الحالة. يوضح الشكل الآتي عمليّة قسمة كثير حدود طويلة، وبالنظر إلى قواعد حساب كثيرات الحدود الموصوفة سابقًا، تستمر عمليّة القسمة الطويلة كما لو كنت تقسم الأعداد الصحيحة، وهكذا ترى في الخطوة الأولى من المثال أنّ المقسوم عليه 1101 يُقسم عليه مرّةً واحدةً أوّل أربعة بتات من الرسالة (1001)، نظرًا لأنهما من نفس الدرجة، والباقي هو 100، أو (1101 XOR 1001). تتمثّل الخطوة التالية في إنزال رقم من كثير حدود الرسالة لتحصل على كثير حدود آخر بنفس درجة C (x)، وفي هذه الحالة هو 1001، ثمّ تحسب الباقي مرّةً أخرى وهو (100) وتستمر حتّى اكتمال الحساب. لاحظ أنّ نتيجة القسمة الطويلة (long division)، التي تظهر في الجزء العلويّ من الحساب، ليست ذات أهميّة كبيرة حقيقةً، وإنّما الباقي (remainder) في النهاية هو المهم.

يمكنك الرّؤية في أسفل الشّكل الآتي أنّ باقي القسمة هو 101، لذلك ستعلم أنّ 10011010000 ناقص 101 سيكون قابلًا للقسمة تمامًا على C (x)، وهذا الذي سيُرسَل. عمليّة الطرح في حساب كثير الحدود هي عمليّة XOR منطقية، لذلك ما يُرسَل فعليًّا هو 10011010101، والذي هو عبارة عن الرسالة الأصلية فقط ملحوقًا بها باقي حساب القسمة الطويلة. يقسم المستقبل كثير الحدود المستلَم على C (x)، وإذا كانت النتيجة 0، فسيستنتج عدم وجود أخطاء؛ أمّا إذا كانت النتيجة غير صفريّة، فقد يكون من الضروري تجاهل الرسالة التالفة، ولكن قد يكون من الممكن تصحيح خطأٍ صغير مع وجود بعض الشيفرات (إذا أثر الخطأ على بت واحد فقط على سبيل المثال). يُطلق على الشيفرة التي تفعّل تصحيح الخطأ شيفرة تصحيح الخطأ (error-correcting code أو اختصارًا ECC).

ولكن من أين أتى كثير الحدود C (x)؟ تكمن الفكرة في اختيار كثير الحدود هذا، بحيث لا يمكن تقسيم رسالة بها أخطاء عليه، فإذا كانت الرسالة المرسلة هي P (x)، فيمكن افتراض أنّ إدخال الأخطاء هو عبارة عن إضافة كثير حدود آخر هو E (x)، لذلك يرى المستقبل P (x) + E (x). الطريقة الوحيدة التي قد يمرّ بها الخطأ دون اكتشافه هي إذا كان من الممكن تقسيم الرّسالة المستلمة على C (x)، وبما أنك تعلم أن P (x) يمكن تقسيمها على C (x)، فقد يحدث هذا فقط إذا أمكن قسمة E (x) على C (x) أيضًا، ولكن الحل هو اختيار C (x) بحيث يكون غير محتملٍ جدًا بالنسبة لأنواع الأخطاء الشائعة، فمن بين أنواع الأخطاء الشائعة هو الخطأ أحادي البت (single-bit error)، والذي يمكن التعبير عنه بـ E (x) = xⁱ عندما يؤثّر على موضع البت i إذا اخترت كثير الحدود ،C (x) بحيث يكون الحدّ الأوّل والأخير (أي الحدان x^k و x⁰) غير صفريّين، فعندئذ يكون لديك بالفعل حدَّا كثير حدود لا يمكن تقسيمهما على حدٍّ واحد E (x)، وبالتالي يستطيع C (x) اكتشاف جميع الأخطاء أحادية البت. من الممكن إثبات أن الأنواع التالية من الأخطاء يمكن اكتشافها بواسطة كثير الحدود C (x):

جميع الأخطاء أحادية البت (single-bit errors)، طالما أنّ الحدين x^k وx⁰ لهما معاملات غير صفريّة.
جميع أخطاء البت المضاعفة (double-bit errors)، طالما أنّ كثير الحدود C (x) له معامل بثلاثة حدود على الأقلّ.
أيّ عدد فردي من الأخطاء (odd number of errors)، طالما يتضمّن كثير الحدود C (x) المعامل (x + 1).

من الممكن استخدام الشيفرات التي لا تكتشف وجود الأخطاء فحسب، بل تتيح أيضًا تصحيح الأخطاء، ولن نتناول تفاصيل هذه الشيفرات هنا نظرًا لأنها تتطلّب رياضيات أعقد من تلك المطلوبة لفهم خوارزميّة CRC، ومع ذلك يجب معرفة مزايا تصحيح الأخطاء مقابل اكتشافها، فقد يبدو تصحيح (correction) الأخطاء للوهلة الأولى أفضل دائمًا من اكتشافها (detection)، لأنه يجب التخلّص من الرسالة عند اكتشاف الأخطاء، ثمّ طلب إرسال نسخةٍ أخرى، وبالتالي يُستهلك حيّز النطاق التراسلي وقد يؤدّي إلى التأخير أثناء انتظار إعادة الإرسال، لكن هناك جانب سلبي للتصحيح، إذ يتطلّب عمومًا عددًا أكبر من البتّات الزائدة لإرسال شيفرة تصحيح أخطاء قويّة (أي قادرة على التعامل مع نفس نطاق الأخطاء) مثل الشيفرة التي تكتشف أخطاءً فقط، وبالتالي بينما يتطلّب اكتشاف الخطأ إرسال مزيدٍ من البتّات عند حدوث أخطاء، فيتطلّب تصحيح الخطأ إرسال مزيدٍ من البتات طوال الوقت، لذلك يميل تصحيح الخطأ إلى أن يكون ذو فائدة أكبر عندما: (1) تكون الأخطاء محتملةً تمامًا، مثل البيئة اللّاسلكية على سبيل المثال، أو (2) تكلفة إعادة الإرسال مرتفعة للغاية، بسبب احتواء التأخير إعادة إرسال رزمة عبر رابط فضائي على سبيل المثال.

يُشار أحيانًا إلى استخدام شيفرات تصحيح الأخطاء في الشبكات باسم تصحيح الأخطاء الأمامي (forward error correction أو اختصارًا FEC)، لأن تصحيح الأخطاء يُعالَج مسبقًا عن طريق إرسال معلومات إضافية، بدلًا من انتظار حدوث الأخطاء والتعامل معها لاحقًا عن طريق إعادة الإرسال، حيث يشيع استخدام آلية FEC في الشبكات اللاسلكية، مثل: 802.11. أي رشقة (burst) أخطاء (أي سلسلة بتات خاطئة متعاقبة) يكون طول الرشقة فيها أقل من k بت (معظم أخطاء الرشقات ذات طول أكبر من k يمكن أيضًا اكتشافها).

تُستخدم ستّة إصدارات من كثير الحدود C (x)على نطاق واسع في بروتوكولات مستوى الرابط، حيث يستخدم الإيثرنت آليّة CRC-32 على سبيل المثال، والذي يُعرَّف على النحو التالي:

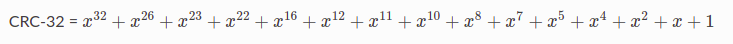
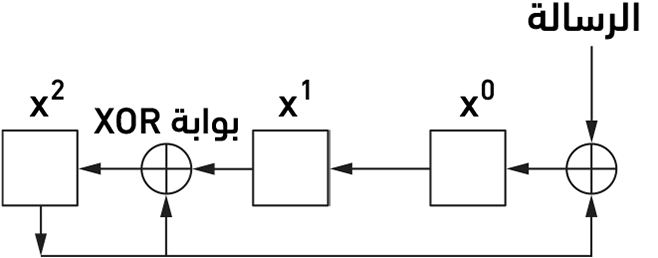
لاحظ أخيرًا أنّ خوارزميّة CRC، رغم أنّها تبدو معقدة، ولكنها تُطبَّق بسهولة في العتاد باستخدام مسجّل إزاحة بحجم k بت وبوّابات XOR، فعدد البتات في مسجل الإزاحة يساوي درجة كثير الحدود المولد (k)، ويوضح الشّكل الآتي العتاد الذي سيستخدمه المولّد x³ + x² + 1 من المثال السابق. حيث تُزاح الرسالة من اليسار بدءًا من البت الأكثر أهميّة وتنتهي بسلسلة k صفرًا المرفقة بالرسالة، فكما في مثال القسمة الطويلة إذا أُزيحت جميع البتّات وطُبِّق عليها XOR بطريقة مناسبة، فسيحتوي المسجّل على الباقي، وهذه هي خوارزميّة CRC (البت الأعلى أهميّةً على اليمين). يُحدَّد موضع بوابات XOR على النحو التالي: إذا سُميَّت البتات في مسجل الإزاحة من 0 إلى k − 1 من اليسار إلى اليمين، فضع بوّابة XOR أمام البت n إذا كان هناك حد xⁿ في كثير الحدود المولّد، وبالتالي ترى بوابة XOR أمام الموضعين 0 و2 للمولد x³ + x² + x⁰.