لوحة المتصدرين
المحتوى الأكثر حصولًا على سمعة جيدة
المحتوى الأعلى تقييمًا في 03/24/24 في كل الموقع
-
لدي سؤال اريد حله عندما اضع خلفية لل body واشغل الصفحه علي الجوال لاتظهر الخلفية الكاملة فقط تظهر ربعها او نصفها كي احل هذه المشكلة وشكرا ..2 نقاط
-
السلام عليكم مساعد في حل مشاكل في الكود ده بلغه الباثيون ده المسائل Replace all vowel to exclamation mark in the sentence. aeiouAEIOU is vowel. وده الكود بتاعي def replace(st): arr = ['a' , 'e' , 'i' , 'o' , 'u'] for i in range(len(st)): if st[i] in arr: st[i] = '!' print(st) replace('aeion') المشاكل موجود في السطر ال 4 مش المفروض هنا يستبدل كل حرف عله ب علامه تعجب1 نقطة
-
السلام عليكم لدي كود تالي اريد تعديل عليه بحث ارسل رمز الاستجابة السريعة للشخص علي ايميله ممكن تعديل كود مرفق في mial->body اريد ارسال رمز qr code ممكن تعديل على كود <?php include('header.php'); use PHPMailer\PHPMailer\PHPMailer; use PHPMailer\PHPMailer\Exception; require 'PHPMailer/src/Exception.php'; require 'PHPMailer/src/PHPMailer.php'; require 'PHPMailer/src/SMTP.php'; // require 'include/phpqrcode/qrlib.php'; // ?> <!--------------------------------------------------------------------------------> <!------------------------------------header--------------------------------------> <!--------------------------------------------------------------------------------> <div class="col-md-9 pan1"> <ol class="breadcrumb" style="background-color: #fff;padding-top:8px;padding-bottom:8px;color:#000;font-size:16px;"> <li><a href="projetcs.php">المشاريع</a></li> <li class="active">القبول</li> </ol> </div> </div> <div class="row"> <div class="col-md-9 pan1"> <div class="panel" style="color:#000;"> <div class="panel-body" style="font-size:14px; padding-left:40px;padding-right:40px;padding-bottom:25px;padding-top:25px;"> <?php if(isset($_GET['id'])){ // $id_p = intval($_GET['id']); $sql = "SELECT * FROM `show_projects_adm` WHERE id_Pro=$id_p"; $query_p = mysqli_query($con,$sql); $rows_p = mysqli_fetch_array($query_p); // $id_pro = intval($_GET['id']); $querypost2="SELECT * FROM `projects` WHERE `id_Pro`=$id_pro"; $result2=mysqli_query($con,$querypost2); $rows2=@mysqli_fetch_array($result2); $id_std = $rows2['Num_STD']; // //$id_std = intval($_GET['id']); $querypost="SELECT * FROM `student` WHERE `id_std`=$id_std"; $result=mysqli_query($con,$querypost); $rows=@mysqli_fetch_array($result); $email_std = $rows['Email_STD']; // // البيانات التي تريد تضمينها في رمز الاستجابة السريعة (QR code) $data = $rows_p['desc_Project']; // اسم الملف الذي يتم حفظه (يمكنك تغييره إلى أي اسم تفضله) $filename = 'img/qr/'.$rows_p['id_Pro'].'_qrcode.png'; // إنشاء رمز QR وحفظه في الملف المحدد QRcode::png($data, $filename); // // Create a new PHPMailer instance $mail = new PHPMailer(true); try { // Server settings $mail->isSMTP(); $mail->Host = 'aaa'; // SMTP server $mail->SMTPAuth = true; $mail->Username = 'aa'; // SMTP username $mail->Password = 'aa'; // SMTP password $mail->SMTPSecure = 'tls'; // Enable TLS encryption, `ssl` also accepted $mail->Port = 587; // TCP port to connect to $mail->CharSet = 'UTF-8'; // Sender and recipient $mail->setFrom('info@aa.com', 'موقع koora'); $mail->addAddress($email_std, 'info'); // Email content $mail->isHTML(true); $mail->Subject = 'قبول المشروع من قبل اللجنة'; // $mail->Body = '<h3>تم القبول المشروع الخاص بك بنجاح</h3>'; $mail->body= // Send email $mail->send(); //echo 'Email has been sent successfully'; } catch (Exception $e) { echo "Message could not be sent. Mailer Error: {$mail->ErrorInfo}"; } //$message = "لقد م قبول تم قبول المقترح بنجاح"; //$headers = "From: info@aa.com"; /// Send // mail($email_std, 'تم قبول المقترح بنجاح', $message); $sql = "UPDATE `projects` SET `Stat`=1 WHERE `id_Pro`='".intval($_GET['id'])."'"; mysqli_query($con,$sql); echo '<div class="col-md-12">'; echo '<div class="text-center alert alert-success" role="alert">تم قبول بنجاح</div>'; echo '<meta http-equiv="refresh" content="3;url=projetcs.php" />'; echo '</div>'; //$send = mysqli_real_escape_string($con,$_POST['username']); /* if(isset($_POST['submit'])){ } */ } ?> </div> </div> </div> </div> <?php include('footer.php'); ?> $mail->body= echo '<tr><td style="font-weight: bold;">QRcode :</td> <td><img src="'.$filename.'" /></td></tr>';1 نقطة
-
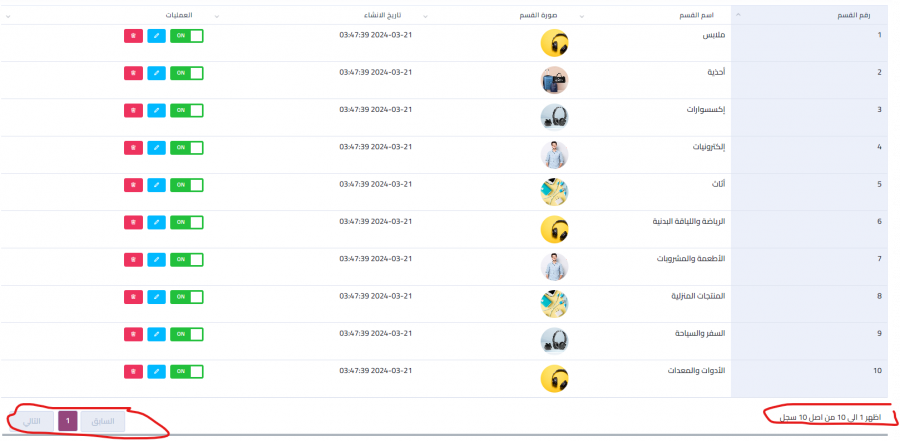
هنا اجلب كل الاقسام بهذه الطريقه public function index() { $categories = Category::orderBy('arrange')->orderByDesc('created_at')->paginate(10); return view('dashboard.catogery.index', compact('categories')); } و هذه هو الجدول الذي يعرض به البيانات بهذه الطريقه <div class="table-responsive"> <table class="table text-md-nowrap" id="example1"> <thead> <tr> <th class="wd-15p border-bottom-0">رقم القسم</th> <th class="wd-15p border-bottom-0">اسم القسم</th> <th class="wd-15p border-bottom-0">صورة القسم</th> <th class="wd-20p border-bottom-0">تاريخ الانشاء</th> <th class="wd-20p border-bottom-0">العمليات</th> </tr> </thead> <tbody> @php $i = 0; @endphp @foreach ($categories as $catogery) @php $i++; @endphp <tr> <td>{{ $i }}</td> </td> <td>{{ $catogery->name_ar }}</td> <td> <div class="image-container"> <img src="{{ asset($catogery->image) }}" alt="Avatar Image"> </div> </td> <td>{{ $catogery->created_at }}</td> <td> <div class="d-flex"> <div class="main-toggle main-toggle-success {{ $catogery->status == true ? 'on' : '' }} btn-sm ml-2" data-catogery-id="{{ $catogery->id }}"> <span></span> </div> <a class="modal-effect btn btn-sm btn-info btn-sm ml-2" data-effect="effect-scale" data-id="{{ $catogery->id }}" data-name_ar="{{ $catogery->name_ar }}" data-name_en="{{ $catogery->name_en }}" data-status="{{ $catogery->status }}" data-arrange="{{ $catogery->arrange }}" data-image="{{ $catogery->image }}" data-toggle="modal" href="#exampleModal2" title="تعديل"><i class="las la-pen"> </i> </a> <a class="modal-effect btn btn-sm btn-danger" data-effect="effect-scale" data-id="{{ $catogery->id }}" data-name="{{ $catogery->name_ar }}" data-toggle="modal" href="#modaldemo9" title="حذف"><i class="las la-trash"></i></a> </div> </td> </tr> @endforeach </tbody> </table> </div> المشكله هنا انه يتم جلب 10 اقسام فقط ولا يتم عرض باقي البيانات في الجدول ولا يوجد paginate في الجدول1 نقطة
-
في لعبة wordGuessing فقط لم افهم وجود failed = 0 ممكن شرح اذا سمحتم1 نقطة
-
1 نقطة
-
هل تفعيل البيئة الافتراضية يؤدي إلى مشاكل مثل اختراق الجهاز ؟ Execution Policy Change The execution policy helps protect you from scripts that you do not trust. Changing the execution policy might expose you to the security risks described in the about_Execution_Policies help topic at https:/go.microsoft.com/fwlink/?LinkID=135170. Do you want to change the execution policy? [Y] Yes [A] Yes to All [N] No [L] No to All [S] Suspend [?] Help (default is "N"): لأن عند تفعيل البيئة الافتراضية وبعد البحث على شات جي بي تي ظهر لي أن هذه الصلاحيات قد تؤدي إلى اختراق ؟ وهل هناك طريقة آمنة ؟1 نقطة
-
لا ضرر في ذلك بل هو أمر ضروري لتفعيل البيئة الإفتراضية في بايثون. فأنت قمت بتنفيذ الأمر التالي Set-ExecutionPolicy RemoteSigned وهو يقوم بتغيير سياسة تنفيذ PowerShell على مستوى الجهاز (LocalMachine) إلى RemoteSigned، وبالتالي يعني أنه لا يمكن تشغيل أي برنامج نصي PowerShell إلا إذا تم توقيعه رقميًا من قبل ناشر موثوق به. وسبب المشكلة هو أن تنفيذ البرامج النصية (السكريبتات) معطل على نظامك، بمعنى أن PowerShell يمنع تشغيل البرامج النصية. حيث يتم تعيين سياسة التنفيذ الافتراضية لـ PowerShell على Restricted، والتي تمنع تنفيذ البرامج النصية لأسباب أمنية، ولتمكين تنفيذها، تحتاج إلى تغيير سياسة التنفيذ إلى مستوى أكثر تساهلاً، وهناك ثلاث سياسات تنفيذ رئيسية في PowerShell: Restricted: السياسة الافتراضية، والتي تمنع جميع عمليات تنفيذ البرامج النصية. RemoteSigned: تسمح بتنفيذ البرامج النصية التي تم إنشاؤها محليًا والبرامج النصية الموقعة عن بُعد من الناشرين الموثوق بهم. Unrestricted: تسمح بتنفيذ جميع البرامج النصية دون أي قيود. الضرر يكمن عند تعيين سياسة التنفيذ إلى Unrestricted1 نقطة
-
1 نقطة
-
هل تقصد أنه بعد توليد الـ QR تريد إرساله في بريد إلكتروني؟ إليك مثال بواسطة مكتبة phpmailer في PHP: <?php use PHPMailer\PHPMailer\PHPMailer; use PHPMailer\PHPMailer\Exception; require 'vendor/autoload.php'; // تحقق من المسار الصحيح لملف autoload.php $mail = new PHPMailer(true); try { // إعداد معلومات البريد الإلكتروني $mail->isSMTP(); $mail->Host = 'smtp.example.com'; $mail->SMTPAuth = true; $mail->Username = 'your_email@example.com'; $mail->Password = 'your_email_password'; $mail->SMTPSecure = 'tls'; $mail->Port = 587; // إعداد المرسل والمستلم $mail->setFrom('your_email@example.com', 'Your Name'); $mail->addAddress('recipient@example.com', 'Recipient Name'); // إعداد محتوى البريد الإلكتروني $mail->isHTML(true); $filename = 'path_to_your_qr_code.png'; $mail->Subject = 'QR Code Email'; $mail->Body = '<h1>QR Code</h1><p>Here is your QR code:</p><img src="cid:qrcode">'; $mail->AltBody = 'Here is your QR code'; // إرفاق الصورة كجزء مضمن في البريد الإلكتروني $mail->addEmbeddedImage($filename, 'qrcode'); // إرسال البريد الإلكتروني $mail->send(); echo 'Message has been sent'; } catch (Exception $e) { echo "Message could not be sent. Mailer Error: {$mail->ErrorInfo}"; } ?> والفكرة هي بإرفاق صورة الرمز الشريطي QR باستخدام الدالة addEmbeddedImage وتعيينها كمرفق مضمن في البريد الإلكتروني، وعرض الصورة في البريد الإلكتروني باستخدام عنوان الرابط cid:qrcode، وبالطبع عليك تغيير path_to_your_qr_code.png إلى مسار الصورة الخاصة برمز QR لديك.1 نقطة
-
انا حلت المكشله وده الكود def replace(st): arr = ['a' , 'e' , 'i' , 'o' , 'u'] word = '' for key in range(len(st)): if st[key].lower() in arr: word += '!' else: word += st[key] return word print(replace('aeioun')) بس في الموقع عاوزني ارجع المتغير ال st حالتها الحمد الله انا هاجي في الاخر وهعمل كده st = world return st1 نقطة
-
1 نقطة
-
ماهي أنواع اختبارات المستخدم user testing ومتى تستخدم وهل هناك منصات عربية مثل أفكار1 نقطة
-
عند تشغيل الكود يظهر خطأ TypeError: 'str' object does not support item assignment وذلك طبيعي لأن السلاسل النصية (strings) في لغة بايثون غير قابلة للتعديل (immutable)، بمعنى أنه لا يمكن تغيير محتوياتها بعد إنشائها، وأنت تحاول تغيير أحرف السلسلة النصية "st" داخل الحلقة، لكن بايثون يمنع ذلك لمنع حدوث نتائج غير مرغوبة. لذا تحتاج إلى إنشاء سلسلة جديدة تحتوي على التغييرات المطلوبة، حاول التفكير في الأمر لكي تستفيد.1 نقطة
-
هل يمكننى الحصول على الشهادة بدون حفظ المشاريع السابقة لانني فعلت كل المشاريع التي ذكرت بدون حفظ اي واحدا منهن واذا اردت ان افعلهن سيستغرق هذا مني وقتا كثيرا1 نقطة
-
ما فهمته هو أنك قمت بتنفيذ المشاريع لكنها غير موجودة على الحاسوب أي لم تقم بحفظها، صحيح؟ في تلك الحالة تستطيع نسخ الأكواد من مستودع المشروع النهائي والذي ستجد الرابط الخاص به في مقدمة أو مدخل كل مسار، لكن المهم هو استيعاب ما تم تنفيذه بالمشروع حيث سيتم سؤالك عن ذلك ولن يفيد نسخ الكود بدون فهم. رغم أني أنصحك بعد فعل ذلك وتنفيذ المشاريع مرة أخرى بمفردك، وستحقق إفادة أكبر لنفسك، ففي المرة الأولى لا أحد يستوعب الأمر بشكل كامل وستجد أن هناك بعض الأمور التي تحتاج مراجعتها واستيعابها مرة أخرى عند التنفيذ بمفردك، أيضًا عند التنفيذ بمفردك ينصب تركيزك على المشروع وليس على متابعة الخطوات مع الشرح، لذا الكثير يظن أنه قادر على تنفيذ مشروع من البداية لأنه قام بمتابعة الشرح فقط ولم يقم بتنفيذ مشروع بمفرده. أما إن كنت تقصد أنك لم تقم برفع المشاريع على GitHub ، فالأمر بسيط ولن يستغرق وقت، وقد تم توضيح مصادر لتعلم كيفية تنفيذ ذلك.1 نقطة
-
1 نقطة
-
مرحبا أريد أن اعرف كيف اجتاز هذه الخطوة لأنني لم استطيع العثور على هذا الزر (Run) وخاصه من الواضح من الذي يشرح لديه نظام Mac OS وكما هو الواضح نظام جهازي Windows.1 نقطة
-
السلام عليكم هل ممكن اجيب ناتج قاسم المشتركه الاكبر باستخدم مكتبه Numpy1 نقطة
-
نعم بالتأكيد. باستخدام مكتبة نامباي يمكن حساب القاسم المشترك الأكبر (GCD) بسهولة. الخطوات هي: استيراد المكتبة: import numpy as np ثم تعريف الأعداد التي تريد حساب GCD لها: a = 12 b = 8 ثم استخدم دالة np.gcd(): result = np.gcd(a, b) إلان يمكنك طباعة الناتج: print(result) الناتج سيكون 4 حيث 4 هو القاسم المشترك الأكبر لـ 12 و 8. بهذه الطريقة يمكن حساب GCD لأعداد أكبر أو لمصفوفات بأكملها بسهولة باستخدام مكتبة نامباي.1 نقطة
-
وعليكم السلام ورحمة الله وبركاته . نعم يمكنك استخدام الدالة gcd فى numpy التى تسمح لك بتمرير رقمين لها وتقوم بارجاع لك ناتج القسمة المشترك الاكبر "Greatest common divisor" . وهذا كود للتوضيح. import numpy as np num1 = 6 num2 = 9 x = np.gcd(num1, num2) print(x) #3 ويمكنك ايضا استخدمها على مصفوفة تحتوى على عدة ارقام و تقوم بارجاع ناتج القسمة الاكبر لجميع هذه الارقام معا . وهذا هو الكود الخاص بها . import numpy as np arr = np.array([20, 8, 32, 36, 16]) x = np.gcd.reduce(arr) print(x) #ُ41 نقطة
-
من شروط الحصول على الشهادة رفع المشاريع على حسابك على GitHub لذلك يجب عليك رفع المشاريع التي قمت بها للحصول على الشهادة ولكن طالما أن التطبيقات لديك على الحاسوب فإنه من السهل رفعها على GitHub ولن تستغرق وقتاً طويلاً ولكن يفضل الإطلاع على الإجابات التالية1 نقطة
-
الأمر هنا يختلف على حسب لغة البرمجة التي تستخدمها و لكن خوازرمية المشكلة تكون مشابهة و يمكنك ترجمتها إلى لغة البرمجة التي تستعملها، و تتضمن العملية إنشاء جدول في قاعدة البيانات لتخزين بيانات المستخدمين أثناء الاستبيان، وإنشاء نموذج يجمع هذه البيانات ويخزنها في قاعدة البيانات، ثم يجب ربط صفحة الاستبيان بالنموذج المناسب لجمع البيانات وتخزينها، و عند اكتمال المستخدم للاستبيان، يمكن استخدام البرمجة النصية للتحقق من الإجابات وتخزينها في قاعدة البيانات لاستخدامها فيما بعد، مثل إنشاء كوبون خصم مخصص للمستخدم. و لإعطاء المستخدم كوبون خصم مخصص له فقط، يمكنك اتباع الخطوات التالية: قم بإنشاء كوبون خصم جديد في قاعدة البيانات وربطه بمعرف المستخدم الذي أكمل الاستبيان. قم بإظهار صفحة أخرى للمستخدم بعد اكتمال الاستبيان تحتوي على كوبون الخصم، و عند إدخاله للكوبون تأكد من معرف المستخدم و تطابقه مع الكود. تنفيذ هذه الخطوات يتطلب المهارات اللازمة في تطوير الويب وقواعد البيانات، ويمكنك استخدام لغة البرمجة التي تتقنها.1 نقطة
-
شكرا على المعلومات و الرد و جزاك الله خير هوا يمكنني عمل لوحة بسيطة و البرمجة ب php and MySQL لاكن باقي كيف يمكنني جلب مفاتيح فك التشفير و كيف يمكنني إرسالها الى المشترك1 نقطة
-
نعرفك في مقال اليوم على لغة جافا Java إحدى لغات البرمجة العريقة عامة الأغراض وذائعة الصيت بين أوساط المطورين، ونكتشف أبرز مميزاتها وعيوبها ومجالات استخداماتها، ونختم المقال بمجموعة من النصائح والخطوات التي تسهل عليك تعلم الجافا من الصفر حتى الاحتراف. ما هي لغة جافا لغة جافا Java هي لغة برمجة عامة الأغراض أطلقتها شركة صن ميكروسيستمز Sun Microsystems عام 1995، وكان الهدف من تطويرها في الأساس إنشاء لغة برمجة محمولة ومستقلة عن نظام التشغيل فخرجوا لنا بلغة البرمجة جافا Java التي اقتبس اسمها من جزيرة جافا المشهورة بإنتاج القهوة وهي كما تعرف المشروب المفضل لدى معشر المبرمجين، كما أن شعار اللغة يأخذ شكل فنجان من القهوة. وفي عام 2009 استحوذت شركة أوراكل Oracle على شركة Sun Microsystems فأصبحت هي المالك الفعلي للغة البرمجة جافا. وعملت على تطوير إصدارات مختلفة من اللغة وأحدث إصدار من جافا عند كتابة هذا المقال هو Java SE 21 الصادر في سبتمبر عام 2023، وهو إصدار طويل الدعم LTS (سينتهي دعمه الرسمي في سبتمبر 2028) وقد فرضت لغة جافا نفسها اليوم كإحدى أشهر وأقوى لغات البرمجة في العالم، كما أنها من لغات البرمجة الأعلى طلبًا في سوق العمل وهي تستخدم في العديد من المجالات والتطبيقات التي سنتعرف عليها في فقرات لاحقة. ما أهمية آلة جافا الوهمية JVM للغة البرمجة جافا؟ تعتمد لغة جافا في تصميمها على مبدأ الكتابة مرة واحدة والتشغيل في أي مكان "write once, run anywhere" مستعينة بما يسمى آلة جافا الوهمية Java Virtual Machine أو ما يعرف اختصارًا JVM، فأي نظام تشغيل مثبت عليه JVM يمكنه تشغيل تطبيقات جافا دون أي تغيير في الكود، وآلة جافا الوهمية أو الافتراضية هي عبارة عن برنامج موجود ضمن نظام التشغيل مهمته تفسير كود البايت لجافا Java bytecode كي يتمكن من العمل على أجهزة مختلفة وأنظمة مختلفة سواء ويندوز أو لينكس أو ماك أو أندرويد …إلخ فهي بمثلة المحرك الذي يحول كود البايت إلى لغة الآلة الخاص بكل نظام. لم تكن هذه الآلية في العمل متاحة في لغات البرمجة الأخرى والتي كانت تتطلب إعادة كتابة التعليمات البرمجية لكل نظام تشغيل على حدا. ولعل هذه الميزة هي أبرز ما ميز لغة جافا عن باقي لغات البرمجة، ولا تقتصر أهمية آلة جافا الوهمية على تمكين برنامج جافا من العمل في أي بيئة تشغيل، بل تساهم الآلة الوهمية كذلك في الحفاظ على ذاكرة برامج جافا وتحسينها فهي تتضمن ميزة تراقب البرنامج بشكل مستمر وتبحث عن أي بيانات مهملة وغير مستخدمة في الذاكرة وإزالتها ما يساهم في زيادة أداء البرامج وسرعتها. مميزات لغة جافا تتميز لغة جافا بالعديد من الجوانب الإيجابية ومن أبرزها: تعد واحدة من لغات البرمجة عالية المستوى وسهلة التعلم. لغة عامة الأغراض ومتعددة الاستخدامات وتصلح لتطوير العديد من التطبيقات. لغة مشهورة وذائعة الصيت وتملك مجتمع دعم كبير ونشيط يضم الكثير من المطورين المحترفين. يمكن تشغيل أكواد جافا على أي نظام تشغيل بفضل آلة جافا الوهمية JVM. توفر ميزات تعزز أداء البرامج مثل ميزة تجميع للبيانات المهملة في الذاكرة ومسحها تلقائيًا. لغة برمجة آمنة وتوفر العديد من المميزات لحماية التطبيقات. تدعم البرمجة الموزعة أي يمكن بسهولة توزيع تطبيقات Java عبر أجهزة متعددة. سلبيات لغة جافا بالرغم من أن لغة جافا تعد واحدة من لغات البرمجة سهلة التعلم لكنها أصعب من لغات أخرى أحدث مثل بايثون وروبي والتي تناسب المبتدئين أكثر. تعد لغة جافا أبطأ من بعض لغات البرمجة الأخرى مثل C وC++. لا توفر الكثير من الأدوات القوية فيما يتعلق بإنشاء واجهات المستخدم الرسومية GUI مقارنة بلغات أخرى مثل بايثون أو C#. استخدام لغة جافا مجاني للاستخدامات الشخصية والتطويرية، لكن شركة أوراكل تفرض رسومًا مالية للاستخدام التجاري لإصدارات جافا من الإصدار 11 والإصدارات الأحدث. استخدامات جافا تتميز لغة جافا Java بكونها لغة عامة الأغراض وهي تصلح للاستخدام في مجموعة واسعة من التطبيقات ومن أبرز استخدامات جافا نذكر: تطوير تطبيقات الجوال (تطبيقات أندرويد Android) تطوير الويب تطوير تطبيقات سطح المكتب برمجة ألعاب الفيديو والألعاب الإلكترونية برمجة تطبيقات الذكاء الاصطناعي وإنترنت الأشياء لنناقش كل استخدام من هذه الاستخدامات وأهمية استخدام لغة البرمجة جافا فيه. تطوير تطبيقات الجوال (تطبيقات أندرويد Android) كانت لغة جافا Java اللغة الافتراضية المعتمدة من قبل جوجل من أجل برمجة تطبيقات الأندرويد وهي توفر العديد من المكتبات والأدوات المساعدة في تطوير تطبيقات جوال أصيلة Native سريعة وعالية الأداء وقادرة على الوصول بسهولة إلى كافة موارد ومميزات الجوال. وبالرغم من أن جوجل طورت فيما بعد لغة كوتلن Kotlin واعتبرتها اللغة البرمجية الجديدة المعتمدة لتطوير تطبيقات أندرويد عام 2019 إلا أن لغة جافا لا تزال مستخدمة بشكل كبير في برمجة تطبيقات الجوال. تطوير الويب تصلح لغة جافا أيضًا للاستخدام في مجال تطوير الويب، فهي توفر مجموعة كبيرة من المكتبات وأطر العمل وواجهات برمجة التطبيقات APIs التي تسهل عليك تطوير تطبيقات الويب نذكر من بينها: Spring وMicroNaut و Google Web Toolkit أو اختصارًا GWT، كما أنها لغة برمجة آمنة وتوفر العديد من الميزات المدمجة التي يحتاجها مطورو الويب لتطوير تطبيقات آمنة وموثوقة مثل ميزة التحكم في الوصول Access control والمصادقة Authentication. تطوير تطبيقات سطح المكتب تساعد لغة جافا على برمجة تطبيقات سطح مكتب متوافقة مع كافة أنظمة التشغيل وذات واجهات مستخدم أنيقة وقادرة على تخزين ومعالجة البيانات بكفاءة، وتوفر العديد من الأدوات المساعدة لتطوير تطبيقات سطح المكتب وأشهرها Java Swing و JavaFX وهي عبارة عن مجموعة أدوات توفر لك ما تحتاجه لبناء واجهات المستخدم الرسومية GUI لتطبيقات سطح المكتب. برمجة الألعاب الإلكترونية تعد لغة جافا Java واحدة من أشهر لغات برمجة الألعاب الإلكترونية وبشكل خاص ألعاب الجوال فهي تدعم ميزة تعدد الخيوط threads والمعالجة على التوازي، وتوفر محركات ألعاب ومكتبات وأطر عمل مساعدة في مجال تطوير الألعاب ثنائية وثلاثية الأبعاد متعددة المنصات مثل jMonkeyEngine و libGDX وLWJGL. ومن أشهر الألعاب المطورة باستخدام لغة البرمجة جافا نذكر: لعبة ماين كرافت Minecraft لعبة Asphalt 6 لعبة Star Wars Galaxies برمجة تطبيقات الذكاء الاصطناعي وإنترنت الأشياء تناسب لغة البرمجة جافا Java تطوير تطبيقات الذكاء الاصطناعي وتعلم الآلة وتطوير تطبيقات مضمنة لإنترنت الأشياء IoT فهي توفر العديد من مكتبات تعلم الآلة، كما توفر واجهات برمجة التطبيقات APIs مفيدة في هذا المجال مثل مكتبة TensorFlow و Scikit learn و JML و Weka والتي يمكن الاعتماد عليها لتطوير تطبيقات ذكاء اصطناعي متوافقة مع مختلف المنصات، كما أنها لغة برمجة قوية قادرة على التعامل بكفاءة مع البيانات الضخمة Big Data وتحليلها بسرعة وفعالية. ما الفرق بين جافا و جافا سكريبت بالرغم من تشابه اسمي اللغتين، إلا أن لغة جافا ولغة جافا سكريبت هما لغتا برمجة مختلفتان تمامًا، ولكل منهم صياغة وطريقة مختلفة في كتابة التعليمات والأكواد البرمجية لكنهما تشتركان في بعض الجوانب وتختلفان في جوانب أخرى. تتشابه هاتان اللغتان بكونهما من لغات البرمجة عالية المستوى والشائعة بين معشر المطورين، لكن لغة البرمجة جافا هي لغة برمجة مصرفة compiled عامة الأغراض تستخدم لإنشاء مختلف أنواع التطبيقات التي تعمل ضمن آلة جافا الافتراضية JVM، أو ضمن متصفح يدعم جافا من خلال ما يعرف باسم بريمجات جافا Java applet وتعتمد لغة جافا بشكل أساسي على نموذج البرمجة كائنية التوجه OOP . أما لغة جافا سكريبت فهي لغة برمجة نصية مفسرة interpreted طورتها شركة Netscape Communications عام 1995 وكان الغرض الأساسي منها هو جعل صفحات الويب تفاعلية وديناميكية تعمل ضمن المتصفح أو من طرف العميل كما أنها أصبحت فيما بعد قادرة على العمل خارج المتصفح والعمل من جانب الخادم بفضل بيئة التشغيل نود جي إس Node.js وتدعم لغة جافا سكريبت كل من نموذج البرمجة الإجرائية ونموذج البرمجة كائنية التوجه بنفس الوقت. ما الفرق بين جافا وكوتلن لغة كوتلن Kotlin هي لغة برمجة منبثقة عن لغة جافا Java وهي تعد كذلك من لغات البرمجة القوية والتي تتشابه مع لغة جافا في كونها لغة كائنية التوجه OOP وتعمل ضمن آلة جافا الافتراضية JVM وتتوافق مع العديد من المنصات والأنظمة، كما أنها لغة عامة الأغراض وتستخدم لتطوير مختلف التطبيقات مثل تطبيقات الجوال والويب. ورغم تشابه اللغتين في عدة جوانب إلا أن لغة كوتلن Kotlin أحدث من لغة جافا، وتضيف عدة تحسينات عليها، إذ توفر كوتلن نظامًا صارمًا للتحقق من الأنواع يسهل على المطورين كشف الأخطاء وصيانة الكود البرمجي، وتوفر ميزات لتعزيز أمان التطبيقات مثل أمان القيم الفارغة Null Safety التي تمنع المبرمج من تعيين قيمة فارغة لمتغير ما، فضلًا عن كون شيفراتها البرمجية أكثر اختصارًا وأسهل مقروئيةً، وتستهلك موارد وذاكرة أقل من نظيرتها المكتوبة بلغة جافا Java، وهي كذلك تمكنك من كتابة توابع برمجية جديدة لتوسيع الأصناف البرمجية classes دون الحاجة إلى تعديل الأصناف نفسها. خطوات تعلم جافا إذا كنت ترغب في تعلم جافا Java ولكنك مشتت ولا تعرف من أين تبدأ، فإليك قائمة بأبرز الخطوات التي تساعدك على تعلم لغة جافا من الصفر حتى الاحتراف: قبل البدء بخطوات تعلم لغة جافا أسس نفسك في الخوارزميات والتفكير المنطقي فهي خطوة أساسية لتعلم أي لغة برمجة وفهمها بصورة أسرع. حدد هدفك من تعلم جافا ونوع التطبيقات الذي تهدف لتطويرها باستخدامها، فهذا يساعدك على التركيز على دراسة المواضيع التي تهمك أكثر من غيرها. تعلم كيفية تثبيت لغة جافا على جهازك وكيفية استخدام أحدد محررات الأكواد أو بيئات التطوير المتكاملة IDE الخاصة بها كي تتمكن من كتابة وتنفيذ أكواد جافا وجرب كتابة أول برنامج لك في جافا. تعلم أساسيات البرمجة بلغة جافا مثل أسلوب كتابة شيفرات جافا ومفاهيم المتغيرات وأنواع البيانات الأساسية وهياكل البيانات في جافا واستخداماتها وكيفيه كتابة تعليمات التحكم كالشروط وحلقات التكرار واستخدام الدوال البرمجية. طبق ما تتعلمه من أساسيات على برامج بسيطة مثل برامج حل المعادلات أو ترتيب مجموعة من البيانات بطرق مختلفة، وتدرب على اكتشاف ومعالجة الأخطاء البرمجية فهذه مهارة أساسية لأي مبرمج. بعد أن تتقن الأساسيات انتقل لتعلم مفاهيم متقدمة في جافا وأهمها مبادئ البرمجة كائنية التوجه OOP ومفاهيم الأصناف والكائنات وتعدد الخيوط Java Multi-threading، والحزم والواجهات، وآلية التعامل مع استثناءات جافا Exceptions، وعمليات الإدخال والإخراج، وغيرها من التقنيات التي تساعدك على بناء تطبيقات متكاملة بلغة جافا. تعلم أهم المكتبات وأطر العمل المفيدة لتطوير التطبيقات التي تهتم بها وفق الهدف أو المجال الذي حددته في الخطوة الأولى، وابدأ بتطوير تطبيقات متكاملة تعزز خبرتك في هذا المجال وطور عدة مشاريع تعزز خبرتك في هذا المجال. ابحث عن فرصة عمل مناسبة للعمل كمطور جافا وبناء مشاريع فعلية لعملاء حقيقين، فالعمل الفعلي هو ما يعزز خبرتك الحقيقة ويساعدك على معرفة متطلبات سوق العمل بشكل أفضل. لا تتوقف عن التعلم أبدًا، فالبرمجة مجال متجدد ومتطور بشكل مستمر وعليك التعلم بصورة مستمرة لتتمكن من الحفاظ على الصدارة ولا تتقادم معلومات. ستجد الكثير من مصادر التعلم المنوعة عبر الانترنت التي تساعدك على تعلم برمجة جافا بصورة ذاتية من دروس ومقالات لتعلم جافا ومقاطع فيديو وكتب ودورات تدريبية وغيرها، لكن من المهم أن تنظم وقتك في التعلم وتختار مصادر تعلم موثوقة تناسب أسلوبك في التعلم ولا تشتت نفسك بكثرة المصادر. كما يمكنك الاطلاع على دورس ومقالات لغة جافا التي تنشرها أكاديمية حسوب بصورة دورية، وإذا واجهت أي تساؤل حول لغة جافا يمكن طرحه في قسم أسئلة البرمجة في الأكاديمية أو في مجتمع حسوب IO ليجيبك عليك نخبة من المبرمجين والمطورين المحترفين. الخلاصة تعرفنا اليوم على لغة البرمجة جافا التي تعد واحدة من لغات البرمجة المشهورة ومتعددة الاستخدامات والتي تصلح لإنشاء مجموعة متنوعة من التطبيقات بدءًا من تطبيقات الهاتف الجوال والألعاب البسيطة وحتى البرامج المتطورة كبرامج المحاسبة وتطبيقات الذكاء الاصطناعي وتحليل البيانات الضخمة، ومهما كان التخصص أو المجال البرمجي الذي تهتم به فإن قرار تعلم الجافا سيكون ملائمًا للعمل بهذا التخصص. اقرأ أيضًا الدليل السريع للغة البرمجة Java تعرف على ماهية جافا Java مدخل إلى أساسيات البرمجة بلغة Java: ما هي البرمجة؟ كيفية كتابة برامج صحيحة باستخدام لغة جافا Kotlin هو جافا الجديد1 نقطة
-
لتعلم الأمن السيبراني (الهاكر الأخلاقي) يتطلب دراسة عدة مجالات: من ضمنها إحدى لغات البرمجة لتساعدك على تطوير أدواتك التي تساعدك في مهامك، ومن أشهر لغات البرمجة في الأمن السيبراني هي لغة البايثون. يتطلب الأمر دراسة أساسيات البايثون من أوامر الطباعة والقراءة والمتغيرات وحلقات التكرار والجمل الشرطية والمكتبات، ومن أهم المكتبات التي يتم دراستها في البايثون 1- Scapy: مكتبة قوية لإنشاء وتحليل حركة الشبكة، تستخدم لإنشاء حزم الشبكة المخصصة وفحص الشبكة. 2- PyCrypto أو معروفة باسم PyCryptodome: تستخدم للتشفير وفك التشفير وإنشاء التوقيعات الرقمية، توفر واجهات للعديد من خوارزميات التشفير. 3- Nmap:أداة معروفة لفحص المنافذ وتحديد الخدمات المتاحة على الخوادم. يمكن استخدامها لتحديد الثغرات وتقييم أمان الشبكة 4- Socket ومن خلالها يتم اختبار المنافذ عبر البروتوكولات المختلفة، وكذلك تكوين منصات الخادم-العميل. إضافة إلى دراسة نظام تشغيل اللينكس وخصوصًا تفريعة كالي لينكس، وكذلك دراسة الشبكات، والهندسة الاجتماعية من الأمور الهامة في مجال الأمن السيبراني (وهي دراسة نقاط ضعف البشر وجمع معلومات عنهم) وبعض علوم الأمن السيبراني الأخرى.1 نقطة
-
توفر نماذج البرمجة طرقًا مختلفة لحل المشكلات البرمجية التي يواجهها المطورون بسيطة فبعض النماذج يناسب حل المشكلات البرمجية البسيطة وبعضها الآخؤ يناسب لحل المشكلات المعقدة ومعرفة كل نموذج من هذه النماذج يساعد المبرمج على اعتماد النموذج الأنسب الذي يلبي متطلبات عمله. وكنا قد تحدثنا في المقال السابق على لغة البرمجة الإجرائية وهو واحد من أقدم نماذج البرمجة المتبعة في تطوير البرامج والتطبيقات، ونكمل الحديث في مقال اليوم عن أحد أشهر نماذج البرمجة التي يحتاج أي مطور لمعرفتها وهو نموذج لغة البرمجة بالكائنات أو البرمجة كائنية التوجه OOP ونتعرف على مبادئ عمله وطريقة تنظيم الشيفرات البرمجية من خلاله وأهم لغات البرمجة التي تستخدم هذا النموذج، كما سنشرح بالتفصيل مفهوم الأصناف Classes والكائنات المشتقة منها Objects والفرق بينهما وأهمية تطبيق هذه المفاهيم في تطوير البرامج الحاسوبية المعقدة وتسهيل صيانتها. أنواع لغات البرمجة تصنف لغات البرمجة إلى أنواع مختلفة بناء على عدة معايير ومن بين هذه المعايير تصنيفها وفق المنهجية المتبعة لهيكلة الشيفرات البرمجية، حيث تقسم لغات البرمجة بناء على هذا المعيار إلى عدة أصناف أو نماذج برمجية تحدد الأساليب المستخدمة لتمثيل عناصر البرنامج وخطوات معالجة البيانات وسير التنفيذ. تقسم لغات البرمجة بناء على هذا المعيار إلى عدة نماذج تشمل: نموذج البرمجة الأمرية Imperative Programming: الذي يصف بالتفصيل المدخلات وكيفية الحصول على المخرجات منها ويندرج تحته نموذج البرمجة الإجرائية procedural programming ونموذج البرمجة بالكائنات. نموذج البرمجة التصريحية Declarative Programming: الذي يعبر عن المهام التي يجب أن ينجزها البرنامج دون أن يصف بالتفصيل سير التنفيذ الخاص به ويندرج تحته البرمجة الوظيفية functional programming والبرمجة المنطقية logic programming. يمكنك معرفة المزيد من المعايير التي تصنف لغات البرمجة بناء عليها وأهم خصائص كل نوع منها من خلال مطالعة مقال أنواع لغات البرمجة وسنفرد مقال اليوم لشرح نموذج البرمجة بالكائنات وأشهر لغات البرمجة التي تعتمده ونكتشف أبرز مزاياها وعيوبها. ما هي لغة البرمجة بالكائنات؟ لغة البرمجة بالكائنات أو بتعبير أدق لغة البرمجة كائنية التوجه Object-Oriented Programming -واختصارًا oop- هي أحد أشهر نماذج البرمجة وقد تم ابتكارها منذ الستينيات وهي تعتمد على تنظيم شيفرات البرامج باستخدام مفهوم الأصناف classes والكائنات المشتقة منها objects بشكل مشابه لكائنات العالم الحقيقي. الصنف class هو بمثابة نموذج أو مخطط عام لتمثيل الكائنات حيث تتضمن الأصناف تعريف البيانات التي تصف الكائنات والوظائف الخاصة التي تصف سلوك الكائنات وتعالج بياناتها وهو يستخدم كقالب لاشتقاق العديد من الأمثلة أو الحالات المختلفة من هذه الكائنات objects، ولهذا السبب يسمى الكائن نسخة من الصنف instance. على سبيل المثال يمكن تعريف صنف يمثل السيارة حيث يكون لكل سيارة سمات أو خصائص تصفها تسمى المتغيرات الأعضاء أو حقول البيانات مثل طراز السيارة وسنة تصنيعها ولونها …إلخ ولها وظائف أو دوال تسمى دوال الصنف class functions تحاكي الأفعال أو السلوكيات التي تقوم بها السيارة مثل تشغيل السيارة وإيقافها وتغيير سرعتها وتحريكها لليمين واليسار …إلخ. كما يجب أن يتضمن الصنف دوال أخرى أهمها الدالة البانية constructor وهي الدالة التي تستدعى بشكل تلقائي عند إنشاء أو اشتقاق كائن من الصنف ويمكن من خلالها تمرير قيم تحدد متغيرات الكائن الجديد ودوال لضبط قيم متغيرات الكائن setter وجلبها getter وبعد اكتمال تعريف الصنف يمكننا اشتقاق كائن لكل سيارة جديدة نريد إنشاءها. توفر البرمجة بالكائنات للمطورين طريقة قوية لتنظيم البرامج وهيكلة التعليمات البرمجية بشكل وكائنات متفاعلة فيما بينها لتأدية المهام المطلوبة وتساعدهم على إنشاء تطبيقات قابلة للصيانة والتوسعة وإعادة الاستخدام وتعديل التعليمات البرمجية لتلبية المتطلبات. مثال برمجي على تعريف صنف وإنشاء كائنات منه قد يكون الشرح السابق لمفهوم البرمجة بالكائنات مربكًا وصعب الفهم لذا سنوضح لك المفاهيم بمثال عملي برمجي، لنفرض أنك تحتاج إلى تطوير برنامج لإدارة مكتبة باستخدام لغة البرمجة بايثون، إذا كنت تستخدم نموذج البرمجة كائنية التوجه لتطوير هذا البرنامج فأول ما ستفكر به هو الأصناف التي ستحتاجها. على سبيل المثال ستحتاج لتعريف صنف يمثل الكتاب وليكن اسمه Book ثم ستفكر في الخصائص أو السمات المميزة لكل كتاب مثل العنوان واسم المؤلف وعدد الصفحات …إلخ. ثم ستفكر في الوظائف التي ستطبق على هذا الكتاب وهي استعارة الكتاب وحجز الكتاب وإعادته للمكتبة إضافة لطريقة البناء init التي تستدعى عند إنشاء كائن أو كتاب جديد من الصنف وتهيئ خصائص هذا الكتاب ودوال الضبط والجلب لكل خاصية. سنحقق هذا الوصف برمجيًا من خلال كتابة الكود التالي بلغة بايثون: # تعريف صنف يمثل كتاب class Book(object): # تعريف الدالة البانية للصنف def __init__(self,title, author, pages): self.title = title self.author = author self.pages = pages # دالة ضبط عنوان الكتاب def setTitle(self, title): self.title = title # دالة جلب عنوان الكتاب def getTitle(self): return self.title # دالة ضبط اسم الكاتب def setAuthor(self, author): self.author = author # دالة جلب اسم الكاتب def getAuthor(self): return self.author # دالة ضبط عدد الصفحات def setNumPages(self, numPages): self.numPages = numPages # دالة جلب عدد الصفحات def getNumPages(self): return self.numPages # دالة لطباعة متغيرات الكتاب def printbook(self): print('تم إنشاء الكتاب التالي') print('------------') print('العنوان: ' , self.title) print('الكاتب: ' , self.author) print('عدد الصفحات: ' , self.pages) # دالة لإعارة الكتاب def borrow_book(self): print(f"{self.title} تمت استعارة كتاب") # دالة لإرجاع الكتاب def return_book(self): print(f"{self.title} تمت إعادة كتاب") # دالة لحجز الكتاب def reserve_book(self): print(f"{self.title} تم حجز كتاب") بعد تعريف الصنف يمكننا في أي مكان في البرنامج إنشاء كائنات والتعامل معها بالشكل التالي: # إنشاء كائن أول من صنف الكتاب book1=Book("البرمجة بلغة بايثون", "أكاديمية حسوب", 480) book1.printbook() book1.borrow_book() print('\n') سنحصل على المخرجات التالية بعد تنفيذ الشيفرة: يمكننا إنشاء كتاب آخر بتنفيذ تعليمة واحدة سهلة بسيطة وهكذا: # إنشاء كائن ثاني من صنف الكتاب book2=Book("البرمجة بلغة جافا سكريبت", "أكاديمية حسوب", 450) book2.printbook() book2.reserve_book() سنحصل أيضًا على المخرجات التالية: لاحظ كيف خلصتنا البرمجة بالكائنات الكثير من العمل ومن تكرار الشيفرة وهذه هي أبرز ميزة تتميز فيها البرمجة كائنية التوجه. يمكنك مطالعة المزيد من المعلومات حول إنشاء الأصناف والكائنات في لغة بايثون في مقال مختصر البرمجة كائنية التوجه OOP وتطبيقها في بايثون. مبادئ لغات البرمجة بالكائنات تعتمد لغات البرمجة بالكائنات على أربع مبادئ أساسية تمكن المبرمجين من تنظيم الشيفرات البرمجية وتقلل أخطاءها وتسهل إعادة استخدامها وصيانتها وتوسيعها في تطبيقات مختلفة. تشمل المبادئ الأربعة للبرمجة كائنية التوجه ما يلي: التغليف Encapsulation تجريد البيانات Abstraction الوراثة Inheritance تعدد الأشكال Polymorphism لنتعرف على كل مبدأ من هذه المبادئ بمزيد من التفصيل! 1. التغليف Encapsulation يشير مبدأ التغليف إلى عملية دمج البيانات والطرق ضمن وحدة مستقلة ومعزولة عن الشيفرات البرمجية الأخرى لها خصوصيتها، ففي البرمجة كائنية التوجه يمكن الوصول إلى بيانات الكائن وتعديلها فقط باستخدام وظائف أو دوال الكائن نفسها فقط وهذا يسمح بإخفاء الحالة الداخلية للكائن عن الكود الخارجي ويحد من صلاحية الوصول إلى بيانات ووظائف كل كائن أو تعديلها خارج نطاق الكائن ويمنع إساءة استخدامها ضمن الكود البرمجي ويضمن تنظيم الكود وموثوقيته. 2. تجريد البيانات Abstraction يمكن اعتبار مبدأ التجريد جزءًا من مبدأ التغليف فهو يساعد على تبسيط الأنظمة المعقدة عن طريق التركيز على المنطق العام للبرنامج وإخفاء تفاصيل التنفيذ عن المستخدمين، فالمقصود بتجريد البيانات في البرمجة بالكائنات إنشاء بنى مجردة عالية المستوى تسهل التعامل مع المهام المعقدة حيث يتم تمثيل خصائص الكائن وإخفاء تفاصيل التنفيذ أو العمليات الداخلية التي تجري على هذه الكائنات عن المستخدمين. ففي مثال الكتاب الوارد سابقًا ستهتم فقط كمستخدم بمعرفة مواصفات الكتاب وطرق التعامل معه من إعارة وحجز وإعادة دون أن تهتم للطريقة التي تنفذ فيها هذه الوظائف ما يهمك أن تستخدمها وتعمل بشكل صحيح دون أن تشغل بالك بتفاصيل عملها. 3. الوراثة Inheritance يسمح مبدأ الوراثة بإمكانية نقل السلوك والبيانات من كائن إلى آخر ويمكن المبرمج من إنشاء أصناف جديدة فرعية أو أبناء من أصناف أساسية موجودة تصبح آباء لها بدلًا من إنشاء أصناف جديدة كل مرة حيث يرث الصنف الابن كل المتغيرات (الصفات) والدوال (الوظائف) الخاصة بالصنف الأب ويمكنه إعادة تعريف وتخصيص الأمور الخاصة به وإضافة ميزات جديدة لها حسب الحاجة مما يسهل تعديل التعليمات البرمجية وتوسيعها. يمكن على سبيل المثال إنشاء صنف أب يمثل مركبة متحركة أو وسيلة نقل ويتضمن الأمور العامة المشتركة ثم استخدامه لإنشاء كائنات أخرى مثل الدراجات النارية أو الشاحنات أو الحافلات. كما يمكن اعتبار صنف الكتاب هو الصنف الأب وإنشاء صنف ابن منه يمثل مجلة وصنف آخر يمثل رواية يرث كل منهما خصائص ووظائف الصنف الأب ويضيف لها خصائص ووظائف إضافية خاصة به وهكذا. 4. تعدد الأشكال Polymorphism يشير مبدأ تعدد الأشكال إلى قدرة الكائنات المختلفة على الاستجابة بشكل مختلف عند استدعاء نفس اسم الدالة، بمعنى آخر استخدام نفس الوظيفة بمنطق مختلف حيث يمكن للكائنات المختلفة امتلاك وظائف أو دوال بنفس الاسم ولكنها تستخدم تعليمات مختلفة. يتضح استخدام هذا المبدأ بشكل جلي في الوراثة فعلى سبيل المثال بالعودة لمثال السيارة إذا كانت السيارة وهي الصنف الأب تحتوي على دالة لتشغيل السيارة تنفذ التعليمات بطريقة معينة فيمكن للمبرمج إعادة تعريفها وتنفيذها بشكل مختلف في الصنف الابن الذي يمثل الدراجات النارية ويمكن معرفة الدالة التي يجب تنفيذها وقت تشغيل الكود. باتباع مبادئ التغليف والتجريد والوراثة وتعدد الأشكال يمكن للمطورين إنشاء برامج قوية وإعادة استخدامها عند الحاجة ويسهل صيانتها وتطويرها. عمومًا، إن شعرت أنك لم تفهم هذه المبادئ فهمًا تامًا ولم تتضح لك اتضاحًا جليًا، فلا تقلق يكفي أن تتعرف عليها وعلى اسمها ثم ستفهما عندما تبدأ بالتطبيق والكتابة بلغة كائنية التوجه. ما معنى خاص ومحمي وعام في البرمجة بالكائنات؟ ستصادف في كافة لغات البرمجة بالكائنات مصطلحات عام وخاص ومحمي وإليك وصفًا موجز لكل مفهوم من هذه المفاهيم. خاص private: يمكن استخدام أي متغير (صفة) أو دالة (وظيفة) من النوع خاص ضمن الكود الموجود داخل الكائن فقط. محمي protected: لا يمكن استخدام أي متغير أو دالة محمية إلا من قبل الكائن نفسه ومن أبنائه. عام public: يمكن استخدام أي متغير أو دالة عامة أو تعديلها في أي مكان خارج الكائن. وتجدر الإشارة لضرورة الكشف عن الحد الأدنى من المعلومات المطلوبة خارج الكائن والحفاظ على خصوصيته قدر المستطاع إلا إذا دعت الضرورة البرمجية لغير ذلك. أشهر لغات البرمجة بالكائنات تستخدم البرمجة كائنات التوجه OOP على نطاق واسع وتعتمدها العديد من لغات البرمجة ومن أبرز لغات البرمجة بالكائنات نذكر: بايثون Python: من أشهر لغات البرمجة الكائنية وأكثرها تفضيلًا في الأوساط البرمجية فهي لغة مرنة وسهلة التعلم ومتعددة الأغراض تصلح لكثير من المجالات أبرزها تطوير الويب وعلوم البيانات والذكاء الصناعي وتعلم الآلة وهي توفر العديد من المكتبات المساعدة التي تسهل عمل المطورين. جافا Java: من أقوى لغات البرمجة كائنية التوجه وهي لغة قوية وآمنة وتتميز بكونها مستقلة وتعمل على كافة أنظمة التشغيل وهي من أبرز لغات تطوير تطبيقات أندرويد،لكن يعاب عليها أنها بطيئة وتستهلك الكثير من الذاكرة. روبي Ruby: لغة برمجة قوية تشبه لغة باثيون من ناحية امتلاكها قواعد صياغة بسيطة سهلة التعلم وهي تدعم البرمجة بالكائنات وتوفر الكثير من الأدوات والمكتبات وأطر العمل التي تسهل عمل المطورين وأبرزها روبي أون ريلز Ruby on Rails. C++: لغة برمجة قوية تدعم نموذج البرمجة كائنية التوجه وتوفر أداء عالي وإدارة جيدة للذاكرة وتملك مجتمع دعم ضخم وهي تصلح لبرمجة أنظمة التشغيل والتطبيقات المضمنة لكنها لغة صعبة التعلم وأقل مرونة من لغات البرمجة الأخرى. C#: لغة برمجة عامة الأغراض تدعم البرمجة الكائنية وتتكامل مع نظام التشغيل ويندوز وهي تستخدم بشكل أساسي لتطوير تطبيقات سطح المكتب وتطبيقات الويب وتصميم الألعاب. PHP: لغة برمجة مثالية لبناء تطبيقات الويب من جانب الخادم وهي لغة مفتوحة المصدر وسهلة الاستخدام أضافت ميزات البرمجة كائنية التوجه منذ الإصدار PHP5 وهي توفر الكثير من دعم المكتبات وأطر العمل وتعتمدها معظم نظم إدارة المحتوى الشهيرة مثل ووردبريس ودروبال. تايب سكريبت TypeScript: هي لغة برمجة مفتوحة المصدر تدعم البرمجة كائنية التوجه وقد طورتها شركة مايكروسوفت بالاعتماد على لغة جافا سكريبت JavaScript وهي تستخدم بشكل أساسي لتطوير تطبيقات الويب الكبيرة، أما لغة جافا سكريبت فبالرغم من كونها لغة تعتمد بشكل كبير على الكائنات لكنها لا تدعم كافة مبادئ البرمجة بالكائنات. إيجابيات وسلبيات لغات البرمجة بالكائنات لكل نموذج برمجي مميزاته وعيوبه وفيما يلي نوضح أهم إيجابيات وعيوب لغات البرمجة كائنية التوجه oop. إيجابيات لغات البرمجة بالكائنات يسمح أسلوب البرمجة بالكائنات بنمذجة مشكلات العالم الحقيقي بشكل أبسط بكثير من باقي النماذج البرمجية. تسهل البرمجة بالكائنات إعادة استخدام التعليمات البرمجية الحالية وتوسيعها باستخدام مبدأ الوراثة بدلاً من الاضطرار إلى إعادة كتابة نفس الكود مرارًا وتكرارًا تخفي البرمجة كائنية التوجه تفاصيل التنفيذ عن المستخدمين الخارجيين وتتيح لهم استخدام الأصناف بسهولة دون الكشف عن تفاصيل تنفيذ كل دالة من الدوال. تنظم البرمجة بالكائنات عملية تصميم البرامج من خلال تمثيلها بالاعتماد على كائنات منفصلة تتفاعل مع بعضها البعض ولكل منها خصائصها وسلوكياتها. تسرع البرمجة الكائنية تطوير البرمجيات وتزيد إنتاجيتها من خلال إمكانية إعادة استخدامها في مشاريع لاحقة. تحسن صيانة البرامج لأن الكائنات معزولة عن بعضها ويمكن حل مشكلاتها وتحسينها دون الحاجة إلى تعديل كامل الكود. تحافظ على أمان البيانات وتحميها من أي تعديلات غير مرغوب بها. سلبيات لغات البرمجة بالكائنات لغات البرمجة بالكائنات صعبة التعلم للمبتدئين ويستغرق فهمها والتعرف على طريقة عملها بشكل جيد وقتًا وجهدًا. تسبب البرمجة بالكائنات زيادة في حجم كود البرامج حيث تتضمن البرامج المطورة باستخدام نموذج البرمجة كائنية التوجه عددًا أكبر من التعليمات البرمجية مقارنة بالبرامج المطورة بنموذج البرمجة الإجرائية. تعد البرامج المطورة باستخدام نموذج البرمجة بالكائنات أبطأ من البرامج المطورة باستخدام نماذج البرمجة الأخرى. قد لا تناسب البرمجة بالكائنات جميع أنواع المشاكل البرمجية كالأنظمة البسيطة إلى حد ما التي يفضل حلها باستخدام نموذج البرمجة الإجرائية أو الأنظمة البالغة التعقيد التي تضطر فيها إلى إنشاء الكثير من مستويات الوراثة لتحقيقها ما يجعل الكود مربك وصعب الفهم والتي يناسبها نموذج البرمجة الوظيفية. الخلاصة تعرفنا في مقال اليوم على نموذج البرمجة بالكائنات OOP وشرحنا أهم المفاهيم والمصطلحات المرتبطة به مثل الصنف والكائن ومبادئ التجريد والتغليف والوراثة وتعدد الأشكال وعددنا أهم لغات البرمجة بالكائنات وأبرز سلبيات وإيجابيات هذا النموذج البرمجي، كل ما عليك الآن هو تطبيق هذه المفاهيم بشكل عملي من خلال إحدى لغات البرمجة التي تدعمها كي تتمكن من فهمها واستيعابها بشكل أفضل. اقرأ أيضًا البرمجة كائنية التوجه مختصر البرمجة كائنية التوجه OOP وتطبيقها في بايثون مفهوم الكائنات Objects والبرمجة كائنية التوجه OOP البرمجة كائنية التوجه (Object Oriented Programming) في PHP تعلم أساسيات البرمجة1 نقطة
-
تستعرض هذه المقالة أربعةً من خوارزميات الأشجار والمخططات، وهي خوارزمية البحث بالعرض أولا BFS، وخوارزمية البحث بالعمق أولا DFS، والبائع المتجول، وخوارزمية كثيرة الحدود للعثور على أصغر غطاء رأسي في مخطط ما. البحث بالعرض أولا Breadth-First Search سنحاول استعمال هذه الخوارزمية في عدة تطبيقات عمليات بحث. البحث عن أقصر مسار من المصدر إلى العقد الأخرى خوارزمية البحث بالعرض أولا BFS هي خوارزمية لتسلق مخطط أو البحث فيها. تبدأ الخوارزمية من جذر الشجرة (أو أيّ عقدة من المخطط، ويُشار إليها أحيانًا باسم "مفتاح البحث" - search key)، ثمّ تستكشف العقد المجاورة أولاً قبل الانتقال إلى المستوى التالي من العقد. اكتُشفت خوارزمية BFS في أواخر الخمسينيات من قبل إدوارد فورست مور Edward Forrest Moore، الذي استخدمها للعثور على أقصر مسار للخروج من متاهة، وقد اكتُشفت أيضًا بشكل مستقل من قبل CY Lee الذي استخدمها في مجال التوجيه السلكي في عام 1961. تفترض خوارزمية BFS الأمور التالية: لن نجتاز أي عقدة أكثر من مرة. تقع العقدة المصدرية (أي العقدة التي نبدأ منها) في المستوى 0. العقد التي يمكننا الوصول إليها مباشرة من العقدة المصدرية ستكون في المستوى 1، والعقد التي يمكننا الوصول إليها مباشرة من عقد المستوى 1 ستكون في المستوى 2 وهكذا دواليك. يشير مستوى عقدة ما إلى أقصر مسار يصل إلى تلك العقدة انطلاقًا من المصدر. انظر المثال التالي: لنفترض أنّ هذا المخطط يمثل طرقا بين عدة مدن حيث تمثل كل عقدة مدينة واحدة، فيما يشير كل ضلع بين عقدتين إلى طريق يربط بينهما، ونحن نريد الانتقال من العقدة 1 إلى العقدة 10. ستكون العقدة 1 هي المصدر، وهذا يجعلها في المستوى 0. نحدد (نلوّن) العقدة 1 لنشير إلى أننا زرناها. يمكننا الذهاب إلى العقدة 2 أو العقدة 3 أو العقدة 4 من العقدة المصدر، أي العقدة 1، لذلك ستكون هناك 3 عقد من المستوى 1. نحدد هذه العقد لنبيّن أنّها مُزارة، ثمّ نعمل عليها. نلوّن العقد المُزارة، حيث نلوّن العقد التي نعمل عليها حاليًا باللون الوردي، تذكّر أنّنا لن نزور العقدة نفسها مرتين. يمكننا الذهاب إلى العقد 6 و 7 و 8 عبر كل من العقدة 2 والعقدة 3 والعقدة 4، وسنحددهذه العقد لنبيّن أنّها مُزارة. مستوى هذه العقد سيساوي (1 +1) = 2. يشير مستوى العقد إلى أقصر مسافة بينها وبين المصدر. على سبيل المثال: بما أن العقدة 8 موجودة في المستوى 2، فهذا يعني أنّ المسافة من المصدر إلى العقدة 8 هي 2. لم نصل بعدُ إلى العقدة المستهدفة وهي العقدة 10، لذا ننتقل إلى العقد التالية. نستطيع الانطلاق من أيّ من عقد المستوى 2، وهي العقدة 6 والعقدة 7 والعقدة 8. ها قد وجدنا العقدة 10 عند المستوى 3، هذا يعني أنّ أقصر مسار من المصدر إلى العقدة 10 هو 3، وقد بحثنا في كل مستوى من مستويات المخطط إلى أن وجدنا أقصر مسار، وإذ ذاك سنمسح الأضلاع التي لم نستخدمها: بعد إزالة تلك الأضلاع التي لم نستخدمها نحصل على شجرة تُسمى شجرة البحث بالعرض أولًا BFS. تُظهر هذه الشجرة أقصر مسار من المصدر إلى جميع العقد الأخرى. مهمتنا الآن هي الانتقال من العقدة المصدر إلى العقد الموجودة في المستوى 1، ثم من عقد المستوى 1 إلى عقد المستوى 2، وهكذا حتى نصل إلى وجهتنا. يمكننا استخدام الطوابير Queues لتخزين العقد التي سنعالجها. لكل عقدة نعمل عليها فإننا ندفع (نضيف) إلى الطابور جميع العُقد الأخرى التي من الممكن اجتيَازها مباشرة لكنّنا لم نفعل بعد. هذه محاكاة للمثال: أولاً، ندفع العقدة المصدر إلى الطابور، فيبدو هكذا: front +-----+ | 1 | +-----+ مستوى العقدة 1 يساوي 0، أي level[1] = 0، نبدأ الآن البحث بالعرض أولا BFS. في البداية، ننزع عقدة من الطابور فنحصل على العقدة 1، يمكننا -انطلاقًا من هذه العقدة- أن نذهب إلى العقدة 4 أو 3 أو 2، لهذا فهذه العقد الثلاث من المستوى الأول، أي level[4] = level[3] = level[2] = level[1] + 1 = 1. سنحددالآن هذه العقد لنبيّن أنّها مُزارَة، ثمّ ندفعها إلى الطابور. front +-----+ +-----+ +-----+ | 2 | | 3 | | 4 | +-----+ +-----+ +-----+ ننزع الآن العقدة 4 من الطابور ونعالجها، نستطيع الذهاب منها إلى العقدة 7، لهذا يكون لدينا: level[7] = level[4] + 1 = 2. والآن نحددالعقدة 7، ثمّ ندفعها إلى الطابور. front +-----+ +-----+ +-----+ | 7 | | 2 | | 3 | +-----+ +-----+ +-----+ من العقدة 3، يمكننا الذهاب إلى العقدة 7 أو العقدة 8، وبما أن العقدة 7 محددة من قبل (أي مُزارة سابقًا)، فإننا نحدد العقدة 8، ونضع level[8] = level[3] + 1 = 2. والآن ندفع العقدة 8 إلى الطابور. front +-----+ +-----+ +-----+ | 6 | | 7 | | 2 | +-----+ +-----+ +-----+ ستستمر هذه العملية حتى نصل إلى وجهتنا أو نُفرِغ الطابور، وتزوّدنا مصفوفة المستويات level بطول أقصر مسار من المصدر. نستطيع تهيئة عناصر مصفوفة المستويات بقيمة اللانهاية، كناية إلى أنّ العقد لم تُزر بعد. انظر المثال التوضيحي لهذا: Procedure BFS(Graph, source): Q = queue(); level[] = infinity level[source] := 0 Q.push(source) while Q is not empty u -> Q.pop() for all edges from u to v in Adjacency list if level[v] == infinity level[v] := level[u] + 1 Q.push(v) end if end for end while Return level يمكننا معرفة المسافة التي تفصل كل عقدة عن المصدر من خلال التكرار عبر مصفوفة المستويات، على سبيل المثال: المسافة إلى العقدة 10 من المصدر مخزّنة في level[10]. قد نريد أحيانًا أن نعرف المسارات الأخرى التي يمكن أن تُوصلنا إلى العقدة انطلاقًا من المصدر، وذلك إلى جانب المسار الأقصر. لفعل هذا نحتاج إلى مصفوفة جديدة نسميها parent، قيمة parent[source] (source هنا تعني العقدة المصدر) ستكون معدومة NULL. نضيف التعليمة parent[v] := u إلى المثال الوهمي عند كل تحديث لمصفوفة المستويات level في حلقة for. لكي تعثر على المسار بعد انتهاء خوارزمية البحث العرضي أولًا، يكفي أن تجتاز المصفوفة parent خلفيًا إلى أن تصل إلى المصدر، والذي يحمل القيمة NULL في هذه المصفوفة. هذا مثال توضيحي يستخدم العودية recursion: Procedure PrintPath(u): if parent[u] is not equal to null PrintPath(parent[u]) end if print -> u وهذا مثال لا يستخدمها وإنما يستخدم التكرارية فقط iteration: Procedure PrintPath(u): S = Stack() while parent[u] is not equal to null S.push(u) u := parent[u] end while while S is not empty print -> S.pop end while تعقيد الخوارزمية: سوف نزور كل عقدة وكل ضلع مرّة واحدة بالضبط، لذا سيكون تعقيد الخوارزمية الزمني O (V + E)، حيث يمثل V عدد العقد، ويمثّل E عدد الأضلاع. البحث عن أقصر مسار ينطلق من المصدر في مخطط ثنائية الأبعاد قد نحتاج أحيانًا إلى العثور على أقصر مسار من مصدر معيّن إلى جميع العقد الأخرى، أو إلى عقدة محدّدة في مخطط ثنائية الأبعاد. على سبيل المثال: نريد أن نعرف عدد التحركات المطلوبة للفارس للوصول إلى مربع معين في رقعة الشطرنج، وهذه حالة خاصة من مشكلة أكبر، حيث تكون لدينا رقعة بعض مربعاتها محظورة (الفارس لا يمكنه الانتقال لبعض المربعات على الرقعة)، وعلينا العثور على أقصر مسار من مربع إلى آخر لا يمر عبر المربعات المحظورة. في مثل هذه الحالات، يمكننا تحويل المربعات أو الخلايا إلى عقد، ونحل هذه المشكلة بسهولة باستخدام خوارزمية البحث بالعرض أولًا BFS. ستكون المصفوفات visited و parent و level جميعها مصفوفات ثنائية الأبعاد. نأخذ جميع التحركات الممكنة لكل عقدة، ونحسب المسافة إلى العقد الأخرى عبر تحليل مسارات التحرك، ثم نضيف مصفوفة أخرى نسميها direction، والتي ستخزّن جميع التركيبات الممكنة للاتجاهات التي يمكننا الذهاب إليها. مثلا، هذه مصفوفة الاتجاهات الخاصة بالتحركات الأفقية والعمودية: +----+-----+-----+-----+-----+ | dx | 1 | -1 | 0 | 0 | +----+-----+-----+-----+-----+ | dy | 0 | 0 | 1 | -1 | +----+-----+-----+-----+-----+ تمثل dx الحركة على المحور الأفقي x بينما تمثل dy الحركة على المحور العمودي y، ولا شك أن هناك طرق أخرى لتمثيل اتجاهات الحركة لكن يُفضل استخدام مصفوفة الاتجاهات لأنها أسهل وأبسط. كذلك هناك الكثير من التركيبات الممكنة للحركة، إذ يمكن أن تكون التحركات قُطرية أو قد تكون أكثر تعقيدًا مثل تحركات الحصان على رقعة الشطرنج. وينبغي أن نضع في حسباننا الأمور التالية: إذا كانت أيّ من الخلايا محظورة فسيكون علينا أن نتحقق في كل حركة محتملة مما إذا كانت الخلية الحالية محظورة أم لا. علينا أن نتحقق أيضًا ممّا إذا كنا قد تجاوزنا الحدودَ، أي حدودَ المصفوفة. سنُعطى عدد الصفوف والأعمدة. انظر المثال التوضيحي التالي: Procedure BFS2D(Graph, blocksign, row, column): for i from 1 to row for j from 1 to column visited[i][j] := false end for end for visited[source.x][source.y] := true level[source.x][source.y] := 0 Q = queue() Q.push(source) m := dx.size while Q is not empty top := Q.pop for i from 1 to m temp.x := top.x + dx[i] temp.y := top.y + dy[i] if temp is inside the row and column and top doesn't equal to blocksign visited[temp.x][temp.y] := true level[temp.x][temp.y] := level[top.x][top.y] + 1 Q.push(temp) end if end for end while Return level ناقشنا سابقًا أن خوارزمية البحث بالعرض أولا BFS لا تصلح إلا للمخططات غير الموزونة unweighted graphs، أما بالنسبة للمخططات الموزونة فسنحتاج إلى خوارزمية ديكسترا. وبالنسبة لدورات الأضلاع السلبية negative edge cycles فسنحتاج إلى خوارزمية بِِلمان - فورد. هناك مسألة أخرى ينبغي الانتباه إليها، وهي أنّ هذه الخوارزمية مخصّصة لإيجاد أقصر مسار من مصدر واحد، فإذا أردت العثور على المسافة من كل عقدة إلى جميع العقد الأخرى ستحتاج إلى استخدام خوارزمية بِلمان - فورد كذلك. البحث عن المكونات المتصلة لمخطط غير موجهة باستخدام خوارزمية BFS يمكن استخدام خوارزمية BFS للعثور على المكونات المتصلة connected components في مخطط غير موجه، ويمكن استخدامها أيضًا للتحقق مما إذا كان المخطط متصلًا أم لا، وسنفترض فيما يلي أنّنا نتعامل مع مخططات غير موجهة. تعريف: يكون المخطط متصلًا connected إذا كان هناك مسار بين كل زوج من الحروف في المخطط. هذا مثال على مخطط متصل: المخطط التالي غير متصل، ولكن يحتوي على مكوّنتين متصلتين: المكونة المتصل الأولى: {a، b، c، d، e} . المكون المتصلة الثانية: {f} خوارزمية BFS هي خوارزمية لاجتياز المخططات، لذا إن بدأت الخوارزمية من عقدة مصدرية ما وانتقلت من عقدة إلى أخرى، ولم تترك عقدة إلا زارتها قبل انتهائها، فيكون المخطط في هذه الحالة متصلًا، أما إن بقيت بعض بعض العقد غير مُزارة، فسيكون المخطط غير متصل. انظر المثال التوضيحي التالي للخوارزمية: boolean isConnected(Graph g) { BFS(v) // هي عقدة مصدرية v if(allVisited(g)) { return true; } else return false; } وهذا تطبيق بلغة C للتحقق مما إذا كان مخططًا متصلًأ غير موجّه أم لا: #include<stdio.h> #include<stdlib.h> #define MAXVERTICES 100 void enqueue(int); int deque(); int isConnected(char **graph,int noOfVertices); void BFS(char **graph,int vertex,int noOfVertices); int count = 0; struct node { int v; struct node *next; }; typedef struct node Node; typedef struct node *Nodeptr; Nodeptr Qfront = NULL; Nodeptr Qrear = NULL; char *visited;// مصفوفة لتتبع العقد المُزارة int main() { int n,e;// يمثل n عدد الحروف، ويمثل e عدد الأضلاع int i,j; char **graph;//adjacency matrix printf("Enter number of vertices:"); scanf("%d",&n); if(n < 0 || n > MAXVERTICES) { fprintf(stderr, "Please enter a valid positive integer from 1 to %d",MAXVERTICES); return -1; } graph = malloc(n * sizeof(char *)); visited = malloc(n*sizeof(char)); for(i = 0;i < n;++i) { graph[i] = malloc(n*sizeof(int)); visited[i] = 'N';// في البداية، تكون جميع العقد غير مزارة for(j = 0;j < n;++j) graph[i][j] = 0; } printf("enter number of edges and then enter them in pairs:"); scanf("%d",&e); for(i = 0;i < e;++i) { int u,v; scanf("%d%d",&u,&v); graph[u-1][v-1] = 1; graph[v-1][u-1] = 1; } if(isConnected(graph,n)) printf("The graph is connected"); else printf("The graph is NOT connected\n"); } void enqueue(int vertex) { if(Qfront == NULL) { Qfront = malloc(sizeof(Node)); Qfront->v = vertex; Qfront->next = NULL; Qrear = Qfront; } else { Nodeptr newNode = malloc(sizeof(Node)); newNode->v = vertex; newNode->next = NULL; Qrear->next = newNode; Qrear = newNode; } } int deque() { if(Qfront == NULL) { printf("Q is empty , returning -1\n"); return -1; } else { int v = Qfront->v; Nodeptr temp= Qfront; if(Qfront == Qrear) { Qfront = Qfront->next; Qrear = NULL; } else Qfront = Qfront->next; free(temp); return v; } } int isConnected(char **graph,int noOfVertices) { int i; // نختار العقدة 0 لتكون عقدة مصدرية BFS(graph,0,noOfVertices); for(i = 0;i < noOfVertices;++i) if(visited[i] == 'N') return 0;//0 implies false; return 1;//1 implies true; } void BFS(char **graph,int v,int noOfVertices) { int i,vertex; visited[v] = 'Y'; enqueue(v); while((vertex = deque()) != -1) { for(i = 0;i < noOfVertices;++i) if(graph[vertex][i] == 1 && visited[i] == 'N') { enqueue(i); visited[i] = 'Y'; } } } للعثور على جميع المكونات المتصلة لمخطط غير موجه، يكفي أن نضيف سطرين إلى شيفرة الدالة BFS. الفكرة هي أن نستدعي الدالة BFS إلى أن تُزار جميع الحروف. هذا هو السطر الأول، المتغير count هو متغير عام مهيء على القيمة 0، وهذا السطر يوضع في بداية دالة BFS: printf("\nConnected component %d\n",++count); وهذا هو السطر الثاني، اجعله في بداية حلقة while في دالة BFS: printf("%d ",vertex+1); نعرّف الآن الدالة التالية: void listConnectedComponents(char **graph,int noOfVertices) { int i; for(i = 0;i < noOfVertices;++i) { if(visited[i] == 'N') BFS(graph,i,noOfVertices); } } خوارزمية البحث بالعمق أولا Depth First Search خوارزمية البحث بالعمق أولًا DFS هي خوارزمية لتسلق مخطط أو البحث فيها، وتبدأ من الجذر وتستكشف العقد على طول كل فرع وتتعمق فيه إلى آخر حدّ قبل أن ترتد backtrack، وقد استُخدِمت نسخة أولية من هذه الخوارزمية من قبل عالم الرياضيات الفرنسي تشارلز بيير Trémaux في القرن التاسع عشر لإيجاد حلول للمتاهات. البحث بالعمق أولًا هي طريقة تحاول العثور على جميع العقد التي يمكن الوصول إليها من العقدة المصدر، وتجتاز خوارزمية DFS عقد مُكوّنة متصلة connected component ما من مخطط خوارزمية البحث بالعرض أولًا، ثم تعرّف شجرة ممتدة spanning tree. كذلك تستكشف خوارزمية البحث بالعمق أولا كل الأضلاع بطريقة منهجية. إذ تبدأ من العقدة المصدرية، وبمجرد الوصول إلى عقدة من المخطط تبدأ خوارزمية DFS في الاستكشاف انطلاقًا منها (على عكس خوارزمية BFS، التي تضعها في طابور لأجل استكشافها لاحقًا). انظر المثال التالي: نجتاز المخطط باستخدام القواعد التالية: نبدأ من المصدر. لن نزور أيّ عقدة مرتين. نلوّن العقد التي لم نزرها بعد باللون الأبيض. نلوّن بالرمادي العقد التي زرناها ولكن لم نزر بعد جميع العقد المتفرّعة منها. نلوّن بالأسود العقد التي اجتزناها بالكامل هي والعقد المتفرعة منها. تبيّن الرسوم التالية هذه الخطوات: الكلمة المفتاحية التي تهمنا والتي نراها فيما سبق هي الضلع الخلفي backedge، فالضلع 5-1 هو ضلع خلفي backedge، لأننا لم ننته بعد من العقدة 1، فالعودة إلى العقدة المصدرية 1 يعني وجود دورة في المخطط. إذا كنا نستطيع الانتقال من عقدة رمادية إلى أخرى في خوارزمية البحث بالعمق أولا، فذلك دليل على أنّ المخطط يحتوي على دورة، وهذه إحدى طرق رصد الدورات في المخططات. يمكننا أن نجعل أيّ ضلع في الدورة كضلع خلفي اعتمادًا على العقدة المصدرية، وترتيب زيارة العقد. على سبيل المثال: لو انتقلنا إلى العقد 5 من العقدة 1 أولا، لوجدنا أنّ الضلع 2-1 أصبح ضلعًا خلفيًا. تسمى الأضلاع التي تنتقل من عقدة رمادية إلى عقدة بيضاء أضلاع الشجرة أو أضلاعًا شجرية tree edge، وإذا أبقينا على أضلاع الشجرة وحذفنا الأضلاع الأخرى، فسوف نحصل على شجرة البحث بالعمق أولا DFS. إذا استطعنا زيارة عقدة مزارة سابقًا في مخطط غير موجه فذلك يعني وجود ضلع خلفي، أمّا بالنسبة للمخططات الموجّهة فسيكون علينا أن نتحقق من الألوان، حيث يكون الضلع خلفيًا فقط إذا كان بمقدورنا الانتقال من عقدة رمادية إلى عقدة رمادية أخرى. أيضًا، في خوارزمية البحث بالعمق أولا، نستطيع تخزين علامات زمنية timestamps لكل عقدة، تخزن هذه العلامات الزمنية معلومات عما حدث للعقد أثناء المعالجة، ونخزّنها في مصفوفتين، مصفوفة f لتخزين أوقات الانتهاء، ومصفوفة d لتخزين أوقات استكشاف العقد: عندما يتغيّر لون العقدة v من الأبيض إلى الرمادي نسجّل الوقت في الموضع d[v]. عند يتغيّر لون عقدة v من الرمادي إلى الأسود، نسجّل الوقت في f [v]. سيبدو المثال التوضيحي لتخزين العلامات الزمنية كما يلي: Procedure DFS(G): for each node u in V[G] color[u] := white parent[u] := NULL end for time := 0 for each node u in V[G] if color[u] == white DFS-Visit(u) end if end for Procedure DFS-Visit(u): color[u] := gray time := time + 1 d[u] := time for each node v adjacent to u if color[v] == white parent[v] := u DFS-Visit(v) end if end for color[u] := black time := time + 1 f[u] := time التعقيد: تُزار كل عقدة وكل ضلع مرة واحدة، لذا فإن تعقيد خوارزمية DFS هو O (V + E)، حيث يمثّل V عدد العقد في المخطط، ويمثل E عدد الأضلاع. التطبيقات على خوارزمية البحث بالعمق أولًا كثيرة، منها على سبيل المثال لا الحصر: العثور على أقصر مسار بين كل زوج من العقد في مخطط غير موجه. رصد الدورات في المخططات. العثور على المسارات. الترتيب التخطيطي (الطوبولوجي). التحقق ممّا إذا كان المخطط ثنائي التجزئة. العثور على المكونات شديدة الاتصال Strongly Connected Component. حل الألغاز التي لها حل واحد. خوارزمية البائع المتجول إن إنشاء مسار يمر عبر كل رأس من رؤوس المخطط مرة واحدة يكافئ ترتيبًا يرتّب حروف ذلك المخطط، ويمكننا استغلال هذه الخاصية لحساب التكلفة الدنيا لعبور كل رأس مرة واحدة بالضبط عبر تجريب كل التبديلات لمجموعة الأعداد من 1 إلى N، وعددها N!. انظر الشيفرة العامة لهذا: minimum = INF for all permutations P // كل التبديلات current = 0 for i from 0 to N-2 // أضف تكلفة الانتقال من عقدة إلى إلى أخرى current = current + cost[P[i]][P[i+1]] // أضف تكلفة الانتقال من العقدة الأخيرة إلى إلى العقدة الأولى current = current + cost[P[N-1]][P[0]] if current < minimum // إن كان ذلك ضروريا minimum حدِّث minimum = current output minimum التعقيد الزمني: هناك N! تبديلة ينبغي معالجتها، وحساب تكلفة كل مسار تستغرق O(N)، من ثم فإنّ هذه الخوارزمية تستغرق مدة O (N * N!). استخدام البرمجة الديناميكية انظر المسار: (1,2,3,4,6,0,5,7) والمسار (1,2,3,5,0,6,7,4) تبقى تكلفة الانتقال من العقدة 1 إلى العقدة 2 ثمّ إلى العقدة 3 كما هي، لذا ليس علينا إعادة حسابها، إذ يمكن أن نحفظ هذه النتيجة لاستخدامها لاحقًا. لنفترض أنّ dp[bitmask][vertex] تمثل الحد الأدنى لتكلفة المسارات التي تعبر جميع الحروف التي قيمة البتّات المقابلة لها فيها bitmask تساوي 1، والتي تنتهي عند الحرف vertex. على سبيل المثال: dp[12][2] 12 = 1 1 0 0 ^ ^ vertices: 3 2 1 0 نظرًا لأنّ 1100 هي التمثيل الثنائي لـ 12، فإنّ dp[12][2] تمثل الانتقال عبر الحرفين 2 و 3 في المخطط عبر مسار ينتهي عند الحرف 2. هذا تطبيق على الخوارزمية بلغة C++: int cost[N][N]; // إن كان ذلك ضروريا N تعديل قيمة int memo[1 << N][N]; // -1 تهيئة كل العناصر بالقيمة int TSP(int bitmask, int pos){ int cost = INF; if (bitmask == ((1 << N) - 1)){ // استكشاف كل العقد return cost[pos][0]; // تكلفة الرجوع } if (memo[bitmask][pos] != -1){ // إن كنا قد حسبنا هذه القيمة سابقا return memo[bitmask][pos]; // فسنعيد القيمة السابقة، فلا داعي لإعادة حسابها } for (int i = 0; i < N; ++i){ if ((bitmask & (1 << i)) == 0){ //إن لم تُكن العقدة مُزارة بعد cost = min(cost,TSP(bitmask | (1 << i) , i) + cost[pos][i]); // زيارة العقدة } } memo[bitmask][pos] = cost; // حفظ النتيجة return cost; } //Call TSP(1,0) قد يكون هذا السطر مبهمًا، لذا سنفصِّله من أجل التوضيح: cost = min(cost,TSP(bitmask | (1 << i) , i) + cost[pos][i]); هنا، تعيّن العبارة bitmask | (1 << i) البتة رقم i في bitmask وتعطيها القيمة 1 دلالة على أنّ الحرف رقم i قد تمت زيارته. تمثّل i الموضوعة بعد الفاصلة قيمة الموضع pos الجديد في هذا الاستدعاء، والذي يمثل الحرف الأخير الجديد. وتضيف العبارةcost[pos][i] تكلفة الانتقال من الحرف الموجود في الموضع pos إلى الحرف i. يُحدّث هذا السطر قيمة cost، ويعطيها أدنى قيمة ممكنة للمرور عبر كل الحروف الأخرى التي لم تُزر بعد. التعقيد الزمني: هناك 2^N قيمة ممكنة لـ bitmask و N قيمة ممكنة لـ pos في الدالة TSP(bitmask,pos). ويستغرق تنفيذ كل دالة O(N) (الحلقة for). وبالتالي يستغرق هذا التطبيق إجمالا مدة O(N^2 * 2^N) لإيجاد الحل النهائي. خوارزمية كثيرة الحدود ومقيدة زمنيًا للعثور على أصغر غطاء رأسي تعريف: ليكن G مخطط، و C مجموعة من حروفها، فنقول أنّ C غطاء رأسي للمخطط G إن كانت تحتوي طرفًا واحدًا على الأقل من كل ضلع من أضلاع المخطط. وفي هذه الفقرة نستعرض خوارزمية كثيرة الحدود للحصول على أصغر غطاء رأسي vertex cover لمخطط متصل غير موجّه. التعقيد الزمني لهذه الخوارزمية يساوي O (n2). هذا مثال توضيحي لخوارزمية أصغر غطاء رأسي، إذ نُدخل إليها مخططًا متصلًا G لتعيد لنا مجموعة C تمثّل أصغر غطاء رأسي لهذا المخطط. Set C <- new Set<Vertex>() Set X <- new Set<Vertex>() X <- G.getAllVerticiesArrangedDescendinglyByDegree() for v in X do List<Vertex> adjacentVertices1 <- G.getAdjacent(v) if !C contains any of adjacentVertices1 then C.add(v) for vertex in C do List<vertex> adjacentVertices2 <- G.adjacentVertecies(vertex) if C contains any of adjacentVertices2 then C.remove(vertex) return C يمكنك استخدام ترتيب الدلو لترتيب الحروف بحسب درجاتها، وبما أن القيمة القصوى للدرجات تساوي (n-1)، حيث يمثّل n عدد الحروف، فستستغرق عمليات الترتيب O(n). ترجمة -بتصرّف- للفصول 41 و 42 و 44 و 53 من كتاب Algorithms Notes for Professionals. اقرأ أيضًا المقال السابق: خوارزميات البحث في النصوص تطبيقات الخوارزميات الشرهة خوارزمية ديكسترا Dijkstra’s Algorithm1 نقطة
-
الرسم التخطيطي أو المخطط هو مجموعة من النقاط والخطوط التي ترتبط ببعضها (يمكن أن تكون فارغة)، وتسمى نقاط المخطط رؤوسًا vertices أو عقدًا nodes، بينما تسمى الخطوط التي تربط رؤوس المخطط أضلاعًا edges أو أقواسًا أو خطوطًا. يعرَّف مخطط G مثلًا كزوْج (V، E)، حيث تمثّل V مجموعة من الحروف، وتمثّل E مجموعة الأضلاع التي تربط تلك الحروف، انظر: E ⊆ {(u,v) | u, v ∈ V} تخزين المخططات هناك طريقتان شائعتان لتخزين المخططات، وهما: مصفوفة التجاور Adjacency Matrix. قائمة التجاور. مصفوفة التجاور مصفوفة التجاور هي مصفوفة تُستخدم لتمثيل مخطط محدود finite graph، وتشير عناصر المصفوفة إلى ما إذا كانت أزواج الرؤوس متجاورة (مترابطة) في المخطط أم لا. وفي نظرية المخططات، نقول أنّ العقدة B مجاورة للعقدة A إذا كنا نستطيع الذهاب من العقدة A إلى العقدة B، وسنتعلم الآن كيفية تخزين العُقد المتجاورة عبر مصفوفة التجاور Adjacency Matrix ثنائية الأبعاد، هذا يعني أننا سنمثل العقد التي تتشارك الأضلاع فيما بينها. نرى في الشكل الموضح أعلاه جدولًا إلى جانب المخطط، ويمثّل هذا الجدول مصفوفة التجاور الخاصة بالمخطط المجاور له، وتمثل Matrix[i][j] = 1 هنا وجود ضلع بين i و j. بالمقابل، سنكتب Matrix[i][j] = 0 إذا لم يكن هناك أيّ ضلع يربطهما. نستطيع وزن تلك الأضلاع، أي إلحاق رقم بكل ضلع -قد يمثل هذا الرقم المسافة بين مدينتين مثلًا-، وهنا نضع الوزن في الموضع Matrix[i][j] بدلًا من 1. والمخطط الموضح أعلاه ثنائي الاتجاه Bidirectional، أو غير موجّه Undirected، أي أنّه إذا كان بإمكاننا الانتقال من العقدة 2 إلى العقدة 1 فيمكننا أيضًا الانتقال من العقدة 1 إلى العقدة 2. إن لم تتحقّق هذه الخاصية نقول أنّ المخطط موجّه Directed. وتوضع أسهم بدل الخطوط إذا كان المخطط موجَّهًا، كما يمكن استخدام مصفوفات التجاور لتمثيل هذا النوع من المخططات. لكن على خلاف المخططات غير الموجّهة، فإن العقد التي لا تشترك في أيّ ضلع تُمثَّل باللانهاية inf في المخططات الموجّهة كما يبيّن الرسم أعلاه. هناك أمر آخر ينبغي الانتباه له، وهو أنّ مصفوفة التجاور الخاصة بمخطط غير موجّه تكون دائما غير متماثلة. انظر الشيفرة التوضيحية pseudo-code التالية لإنشاء مصفوفة التجاور، حيث يمثل N عدد العُقد: Procedure AdjacencyMatrix(N): Matrix[N][N] for i from 1 to N for j from 1 to N Take input -> Matrix[i][j] endfor endfor فيما يلي طريقة أخرى لتعبئة المصفوفة، يمثل N فيها عدد العُقَد بينما يمثل E عدد الأضلاع: Procedure AdjacencyMatrix(N, E): Matrix[N][E] for i from 1 to E input -> n1, n2, cost Matrix[n1][n2] = cost Matrix[n2][n1] = cost endfor يمكنك إزالة السطر Matrix[n2][n1] = cost من الشيفرة في المخططات الموجّهة. عيوب استخدام مصفوفة التجاور إحدى المشاكل التي تنجم عن استخدام مصفوفات التجاور هو أنّها تستهلك مقدارا كبيرًا من الذاكرة، فمهما كان عدد أضلاع المخطط، سنحتاج دائمًا إلى مصفوفة بحجم N*N، حيث يمثّل N عدد العُقد. أما إذا كانت هناك 10000 عقدة في المخطط فسنحتاج مصفوفة بحجم 4 * 10000 * 10000، أي حوالي 381 ميغابايت، وهذا مضيعة للذاكرة، علمًا أنّ الكثير من المخططات لا تحتوي إلا القليل من الأضلاع. وبفرض أنّنا نريد أن نعرف العقد التي يمكننا الوصول إليها انطلاقًا من العقدة u، فسنحتاج إلى التحقق من الصفّ الخاص بـ u في المصفوفة بالكامل، وهذا سيكلفنا الكثير من الوقت. والفائدة الوحيدة لمصفوفة التجاور هي أنها تمكّننا من العثور بسهولة على مسار بين عقدتين مثل u-v، وكذلك تكلفة cost ذلك المسار، أي مجموع أوزان الأضلاع التي تؤلف المسار. شيفرة جافا التالية تطبق الشيفرة العامّة أعلاه: import java.util.Scanner; public class Represent_Graph_Adjacency_Matrix { private final int vertices; private int[][] adjacency_matrix; public Represent_Graph_Adjacency_Matrix(int v) { vertices = v; adjacency_matrix = new int[vertices + 1][vertices + 1]; } public void makeEdge(int to, int from, int edge) { try { adjacency_matrix[to][from] = edge; } catch (ArrayIndexOutOfBoundsException index) { System.out.println("The vertices does not exists"); } } public int getEdge(int to, int from) { try { return adjacency_matrix[to][from]; } catch (ArrayIndexOutOfBoundsException index) { System.out.println("The vertices does not exists"); } return -1; } public static void main(String args[]) { int v, e, count = 1, to = 0, from = 0; Scanner sc = new Scanner(System.in); Represent_Graph_Adjacency_Matrix graph; try { System.out.println("Enter the number of vertices: "); v = sc.nextInt(); System.out.println("Enter the number of edges: "); e = sc.nextInt(); graph = new Represent_Graph_Adjacency_Matrix(v); System.out.println("Enter the edges: <to> <from>"); while (count <= e) { to = sc.nextInt(); from = sc.nextInt(); graph.makeEdge(to, from, 1); count++; } System.out.println("The adjacency matrix for the given graph is: "); System.out.print(" "); for (int i = 1; i <= v; i++) System.out.print(i + " "); System.out.println(); for (int i = 1; i <= v; i++) { System.out.print(i + " "); for (int j = 1; j <= v; j++) System.out.print(graph.getEdge(i, j) + " "); System.out.println(); } } catch (Exception E) { System.out.println("Something went wrong"); } sc.close(); } } لتشغيل الشيفرة أعلاه، احفظ الملف، ثم صرّف compile الشيفرة باستخدام التعليمة الآتية: javac Represent_Graph_Adjacency_Matrix.java انظر المثال التالي الذي يوضح هذا: $ java Represent_Graph_Adjacency_Matrix Enter the number of vertices: 4 Enter the number of edges: 6 Enter the edges: 1 1 3 4 2 3 1 4 2 4 1 2 The adjacency matrix for the given graph is: 1 2 3 4 1 1 1 0 1 2 0 0 1 1 3 0 0 0 1 4 0 0 0 0 تخزين المخططات (قوائم التجاور) قائمة التجاور هي مجموعة من القوائم غير المرتبة تُستخدم لتمثيل المخططات المحدودة finite graphs، وتصف كل قائمة في المجموعة جيرانَ كلّ حرف من حروف المخطط. وميزة قوائم التجاور أنّها تحتاج مساحة ذاكرة أقل لتخزين المخططات. انظر المثال التالي عن مخططٍ ومصفوفة التجاور الخاصة به: وهذه قائمة التجاور الخاصة بالمخطط أعلاه: تسمى هذه القائمة قائمةَ التجاور adjacency list، وتوضّح الروابط بين العقد. نستطيع إن شئنا تخزين هذه المعلومات باستخدام مصفوفة ثنائية الأبعاد، لكن هذا سيكلفنا نفس مقدار الذاكرة الذي يتطلّبه تخزين مصفوفة التجاور. بدلاً من ذلك، سنستخدم الذاكرة المخصّصة ديناميكيًا لتخزين هذه القيم. تدعم العديد من لغات البرمجة نوعي البيانات المتجهات Vector والقوائم List ، والتي يمكننا استخدامها لتخزين قائمة التجاور، وهكذا لن يكون علينا تحديد حجم القائمة إذ يكفي أن نحدّد الحد الأقصى لعدد العقد. انظر الشيفرة العامة لذلك، حيث يمثل maxN الحد الأقصى للعُقد، بينما يمثل E عدد الأضلاع، ويشير التعبير x, y إلى وجود ضلع يربط بين x وy: Procedure Adjacency-List(maxN, E): edge[maxN] = Vector() for i from 1 to E input -> x, y edge[x].push(y) edge[y].push(x) end for Return edge وبما أنّ هذا المخطط غير موجّه فإنّ وجود ضلع من x إلى y يستلزم وجود ضلع معاكس، أي ضلعٍ من y إلى x، ولن تتحقق هذه الخاصية في المخططات غير الموجّهة. أما بالنسبة للمخططات الموزونة فسنحتاج إلى تخزين التكلفة (الوزن) أيضًا، من خلال إنشاء متجه أو قائمة أخرى باسم cost[] لتخزينها، انظر الشيفرة العامة لذلك: Procedure Adjacency-List(maxN, E): edge[maxN] = Vector() cost[maxN] = Vector() for i from 1 to E input -> x, y, w edge[x].push(y) cost[x].push(w) end for Return edge, cost يمكننا الآن أن نعثر بسهولة على العقد المتصلة بعقدة ما وعددها أيضًا، وسنحتاج وقتًا أقل مقارنة بمصفوفة التجاور. بالمقابل، ستكون مصفوفة التجاور أكثر كفاءة إن احتجنا إلى معرفة ما إذا كان هناك ضلع بين u وv. مقدمة إلى نظرية الرسوم التخطيطية نظرية المخططات أو الرسوم التخطيطية Graph Theory هي فرع من فروع الرياضيات يهتم بدراسة الرسوم التخطيطية، وهي كائنات رياضية تُستخدم لنمذجة العلاقات الزوجية بين الكائنات. طُوِّرت نظرية المخططات من قبل اختراع الحاسوب، إذ كتب ليونهارت أويلر Leonhard Euler ورقة حول جسور كونيجسبرج السبعة Seven Bridges of Königsberg والتي تُعدّ أوّل ورقة علمية عن نظرية المخططات، وأدرك الناس منذ ذلك الحين أنه إذا أمكننا تحويل المشاكل إلى مسائل من نوع مدينة-طريق City-Road، فيمكننا حلها بسهولة باستخدام نظرية المخططات. وهناك تطبيقات عديدة لهذه النظرية، لعل أشهرها هو العثور على أقصر مسافة بين مدينتين. فمثلا، ينبغي أن تمرّ عبر العديد من المُوجّهات routers عندما تدخل موقعًا إلكترونيا، انطلاقًا من الخادم، لكي تصل محتويات الموقع إلى حاسوبك. تساهم نظرية المخططات هنا في العثور على الموجّهات التي ينبغي المرور عبرها للوصول إلى حاسوبك في أسرع وقت. كما تُستخدم خلال الحروب لتحديد الطريق الذي يجب قصفه لقطع العاصمة عن المدن الأخرى. وسنتعلم فيما يلي بعض الأساسيات لهذه النظرية. إليك تعاريف من المهم الاطلاع عليها ومعرفتها: المخططات: لنقل أنّ لدينا 6 مدن، نرقّم هذه المدن من 1 إلى 6. سننشئ الآن مخططًا يمثّل هذه المدن، حيث تمثل الرؤوسُ المدن، مع ربط المدن التي تربطها طرق فيما بينها بأضلاع. هذا مخطط بسيط لتمثيل المدن والطرق الرابطة بينها، ونسمي هذه المدن في نظرية المخططات عقدًا Nodes أو حروفًا Vertex فيما نسمّي الطرق أضلاعًا Edge. يمكن أن تمثل العقدة أشياءً كثيرة، إذ قد تمثّل مدنًا أو مطارات أو مربّعات على رقعة الشطرنج. بالمقابل، تمثل الأضلاع العلاقات بين تلك العقد. مثلًا، يمكن أن تمثّل هذه العلاقات الوقت اللازم للانتقال من مطار إلى آخر، أو نقلة الفارس من مربّع إلى المربعات الأخرى على رقعة الشطرنج، وغير ذلك. تمثيل لمسار الفارس على رقعة الشطرنج وببساطة، تمثّل العقدة أيّ نوع من الكائنات، وتمثّل الأضلاع العلاقات بين تلك الكائنات. العقدة المتجاورة Adjacent Node: تكون B مجاورة لـ A إذا اشتركت عقدة A مع عقدة أخرى B في ضلع واحد، أي نقول أنّ العقدتين متجاورتان إذا اتصلت عقدتان اتصالًا مباشرًا، ويمكن لكل عقدة أن يكون لها عدة عقد مجاورة. المخططات الموجّهة وغير الموجّهة Directed and Undirected Graph: توضع علامات توجيهية (مثل الأسهم) على الأضلاع في المخططات الموجّهة للدلالة على أنّ الضلع أحادي الاتجاه. من ناحية أخرى، تحتوي أضلاع المخططات غير الموجّهة على علامات اتجاه على كلا الجانبين، للدلالة على أنها ثنائية الاتجاه. لكن تُحذف علامات التوجيه تلك في الغالب من المخططات غير الموجّهة، وتمثّل حينها الأضلاع كخطوط وحسب. وإذا افترضنا وجود حفلٍ في مكان ما، فسنمثّل الأشخاص الحاضرين بالعُقد، وسنرسم خطًا بين شخصين إذا تصافحا. لا شك أن هذه المخططات غير موجّهة هنا، لأنّه إذا صافح عمرو زيدًا فهذا يعني أنّ زيدًا صافح عَمرًا كذلك، فهي عملية ثنائية. بالمقابل، إذا رسمنا ضلعًا من عمرو إلى زيد إن كان زيد يقدّر عَمرًا ويحترمه فإنّ هذه المخططات ستكون موجّهة، ذلك أن الإعجاب لا يشترط أن يكون متبادلًا. يُطلق على النوع الأول مخططات غير موجّهة undirected graphs، وتسمّى الأضلاع أضلاعًا غير موجّهة undirected edges، بالمقابل، يسمّى النوع الثاني مخططات موجّهة directed graph وتسمّى الأضلاع أضلاعًا موجّهة directed edges. المخططات الموزونة وغير الموزونة Weighted and Unweighted Graph: المخطط الموزون هو مخطط يكون لكلّ ضلع من أضلاعه رقم (وزن)، يمكن أن تمثّل هذه الأوزان التكاليف أو الأطوال أو السعات وغير ذلك، وذلك اعتمادًا على المشكلة المطروحة. بالمقابل، المخططات غير الموزونة هي مخططات نفترض أنّ أوزان جميع أضلاعها متساوية (تساوي1 افتراضيًا ). المسارات: يمثّل المسار طريقًا للانتقال من عقدة إلى أخرى ويتألّف من سلسلة من الأضلاع، ولا شيء يمنع وجود عدة مسارات بين عقدتين. في المثال أعلاه، هناك مساران من A إلى D، الأول هو A-> B ،B-> C ،C-> D ، وكلفته (مجموع أوزان الأضلاع التي تؤلّفه) هي 3 + 4 + 2 = 9، أما المسار الآخر فهو A-> D، وكلفته 10. يقال أن المسار الذي يكلّف أدنى قدر هو المسار الأقصر. الدرجة degree: درجة الحرف degree of a vertex هي عدد الأضلاع المرتبطة به، فإذا كان هناك ضلع يرتبط بالحرف في كلا الطرفين (حلقة loop)، فسيُحسب مرتين. يكون للعُقد في المخططات الموجّهة نوعان مختلفان من الدرجات: الدرجة الداخلية In-degree: عدد الأضلاع التي تشير إلى العقدة. الدرجة الخارجية Out-degree: عدد الأضلاع التي تنطلق من العقدة الحالية وتشير إلى العقد الأخرى. بالنسبة للمخططات غير الموجّهة، يكون هناك نوع واحد طبعا، ويُسمّى درجة الحرف. بعض الخوارزميات المتعلقة بنظرية المخططات: خوارزمية بلمان فورد Bellman–Ford خوارزمية ديكسترا Dijkstra خوارزمية فورد فولكرسون Ford–Fulkerson خوارزمية كروسكال Kruskal. خوارزمية الجار الأقرب Nearest neighbour algorithm. خوارزمية بْرِم Prim. خوارزمية البحث العميق أولا Depth-first search. خوارزمية البحث العريض أولًا Breadth-first search. سوف نستعرضُ بعض هذه الخوارزميات لاحقًا. الترتيب الطوبولوجي Topological Sort يرتّب الترتيب الطوبولوجي حروف مخطط موجّه ترتيبًا خطيًا، إذ يضعها في قائمة مُرتّبة حسب الأضلاع الموجّهة التي تربط تلك الحروف. وليكون هذا الترتيب ممكنا، يجب ألّا يحتوي المخطط على دورة موجّهة directed cycle، فإن كان لدينا مخطط G = (V, E)، فالترتيب الخطي رياضيًا هو ترتيب متوافق مع المخطط، أي يحقّق ما يلي: إن كانت G تحتوي الضلع (u, v) ∈ E الذي ينتمي إلى E وينطلق من الحرف u إلى v، فستكون u أصغر من v وفق هذا الترتيب. وهنا من المهم ملاحظة أنّ كلّ مخطط موجّه غير دوري directed acyclic graph، أو DAG اختصارًا له ترتيب طوبولوجي واحد على الأقل، وهناك عدد من الخوارزميات التي تمكّننا من إنشاء ترتيب طوبولوجي لمخطط موجّه غير دوري في وقتٍ خطي، هذا مثال عام على إحداها: استدع دالة depth_first_search(G) لحساب أوقات الإنتهاء finishing times بـ v.f لكل حرف v عقب الانتهاء من حرف ما، أدرِجه في مقدّمة قائمة مرتبطة linked list. يُحدَّد الترتيب الطوبولوجي بقائمة الحروف المرتبطة التي نتجت من الخطوتين السابقتين. يمكن إجراء ترتيب طوبولوجي في مدة V + E، لأنّ "خوارزمية البحث العميق أولًا depth-first search" تستغرق مدّة (V + E) ـ كما ستستغرق Ω(1) (وقت ثابت) لإدراج كل الحروف |V| في مقدمة القائمة المرتبطة. تستخدم العديدُ من التطبيقات المخططاتَ الموجّهة الدورية directed acyclic graphs لتمثيل الأسبقية بين الأحداث، إذ يُستخدم الترتيب الطوبولوجي للحصول على الترتيب الصحيح لمعالجة كل حرف من حروف المخطط. وقد تمثّل حروف المخططُ المهامَ التي يتعيّن إنجازها، فيما تمثل الأضلاع أسبقية تنفيذ تلك المهام، وهكذا يمثّل الترتيب الطوبولوجي التسلسل المناسب لأداء مجموعة المهام الموضّحة في V. مثال ليكن v حرفًا يمثّل مهمّة Task(hours_to_complete: int)، بحيث يمثّل الوسيط hours_to_complete الوقت المُستغرَق لتنفيذ المهمة. فمثلًا، تمثّل Task(4) مهمّة تستغرق 4 ساعات لإكمالها. من جهة أخرى، يمثّل ضلع e قيمة Cooldown(hours: int)، والتي تمثّل المدة الزمنية التي تنقضي قبل استئناف المهمة التالية (أي التي يشير إليها الضلع) بعد الانتهاء من المهمة الحالية (التي ينطلق منها الضلع). فإن كان هناك ضلع Cooldown(3) يربط بين مهمّتين أ و ب، فذلك يعني أنه بعد الانتهاء من المهمة أ، ستحتاج أن تنتظر 3 ساعات حتى تستطيع تنفيذ المهمة ب (مثلا ليبرد المحرّك). فيما يلي، المخطط غير الدوري والموجّه dag يحتوي 5 رؤوس: A <- dag.add_vertex(Task(4)); B <- dag.add_vertex(Task(5)); C <- dag.add_vertex(Task(3)); D <- dag.add_vertex(Task(2)); E <- dag.add_vertex(Task(7)); نربط الحروف عبر أضلاع موجّهة بحيث يكون المخططات غير دوري، انظر: // A ---> C -----+ // | | | // v v v // B ---> D ---> E dag.add_edge(A, B, Cooldown(2)); dag.add_edge(A, C, Cooldown(2)); dag.add_edge(B, D, Cooldown(1)); dag.add_edge(C, D, Cooldown(1)); dag.add_edge(C, E, Cooldown(1)); dag.add_edge(D, E, Cooldown(3)); ستكون هناك ثلاثة تراتيب طوبولوجية ممكنة بين A وE: A -> B -> D -> E A -> C -> D -> E A -> C -> E رصد الدورات في المخططات الموجهة باستخدام الاجتياز العميق أولا Depth First Traversal إذا نتج عن الاجتياز العميق أولًا ضلعٌ خلفي back edge، فذلك يعني أنّ المخطط الموجّه يحتوي دورة cycle. والضلع الخلفي هو ضلع ينطلق من عقدة ويعود إليها أو إلى إحدى أسلافها في شجرة بحث عميق أولًا Depth-first search اختصارًا DFS. بالنسبة لمخطط غير متصل disconnected graph، سنحصل على غابة بحث عميق أولا أو غابة DFS وهي اختصار لـ DFS forest، لذلك سيكون عليك التكرار على جميع الحروف في المخطط لإيجاد أشجار البحث العميق أولًا والمنفصلة disjoint DFS trees. فيما يلي تنفيذ بلغة C++: #include <iostream> #include <list> using namespace std; #define NUM_V 4 bool helper(list<int> *graph, int u, bool* visited, bool* recStack) { visited[u]=true; recStack[u]=true; list<int>::iterator i; for(i = graph[u].begin();i!=graph[u].end();++i) { if(recStack[*i]) شرح السطر السابق في الشيفرة: عند إيجاد حرف v في مكدس التكرارية الخاص باجتياز DFS، أعِد true، تابع المثال الآتي: return true; else if(*i==u) // في حال كان هناك ضلع من الحرف إلى نفسه return true; else if(!visited[*i]) { if(helper(graph, *i, visited, recStack)) return true; } } recStack[u]=false; return false; } هنا تستدعي دالة التغليف الدالةَ helper على كل حرف لم يُزَر بعد، وتعيد دالة helper القيمة true عند رصد ضلع خلفي في الشجيرة، وإلا فإنها تعيد false، تابع المثال الآتي: bool isCyclic(list<int> *graph, int V) { bool visited[V]; // مصفوفة لتتبع الأحرف المُزارة سلفا bool recStack[V]; // مصفوفة لتتبع الأحرف في المكدس التكراري للاجتياز for(int i = 0;i<V;i++) visited[i]=false, recStack[i]=false; // تهيئة جميع الأحرف على أنها غير مُزارة تكراريًا for(int u = 0; u < V; u++) // التحقق اليدوي مما إذا كانت كل الأحرف مُزارة { if(visited[u]==false) { if(helper(graph, u, visited, recStack)) // التحقق مما إذا كانت شجرةُ “بحثٍ عميقٍ أولًا” تحتوي دورة. return true; } } return false; } /* Driver function */ int main() { list<int>* graph = new list<int>[NUM_V]; graph[0].push_back(1); graph[0].push_back(2); graph[1].push_back(2); graph[2].push_back(0); graph[2].push_back(3); graph[3].push_back(3); bool res = isCyclic(graph, NUM_V); cout<<res<<endl; } تكون النتيجة كما هو موضّح أدناه، أن هناك ثلاثة أضلاع خلفية في المخططات، واحد بين الحرفين 0 و 2؛ وآخر بين الحروف 0 و1 و2؛ والحرف 3. والتعقيد الزمني للبحث يساوي O (V + E)، حيث يمثّل V عدد الحروف، وE يمثّل عدد الأضلاع. خوارزمية Thorup كيف يمكن العثور على أقصر مسار من حرف (مصدر) معيّن إلى أيّ حرف آخر في مخطط غير موجّهة؟ قدّم "ميكيل توغوب Mikkel Thorup" -نُطْقُ اسمه من الدانماركية- أول خوارزمية تحل هذه المشكلة. يساوي التعقيد الزمني لهذه الخوارزمية O (m). وفيما يلي الأفكارُ الأساسية التي تعتمد عليها الخوارزمية: هناك عدّة طرق للعثور على الشجرة المتفرّعة spanning tree في مدة O (m) (لن نذكر هذه الطرق هنا)، سيكون عليك إنشاء الشجرة المتفرّعة من الضلع الأقصر إلى الأطول، وسينتج عن ذلك غابة (مجموعة من الأشجار غير المتصلة بالضرورة) تحتوي العديد من المكوّنات المتصلة قبل أن تنمو كاملةً. اختر عددًا صحيحًا b (b> = 2)، ولا تأخذ بالحسبان إلّا الغابات المتفرّعة ذات الطول الأقصى b ^ k، ثم ادمج المكونات المتشابهة في كل شيء ولكن تختلف في قيمة k. سنسمّى أصغر قيم k مستوى المكوّن level of the component. ثم ضع المكوّنات بعد هذا في الشجرة في المكان المناسب بحيث يكون الحرف u أبًا للحرف v إذ كان u هي أصغر مكوّن مختلف عن v ويحتوي v بشكل كامل. الجذر سيكون المخطط بأكمله، أمّا الأوراق فهي الحروف المفردة single vertices في المخطط الأصلي (مستواها يساوي سالب ما لا نهاية). ستحتوي الشجرة على O (n) عقدة. حافظ على المسافة بين كل مكوّن وبين المصدر كما هو الحال في خوارزمية Dijkstra، تساوي مسافة مكوّن يحتوي أكثر من حرفٍ المسافةَ الأقل بين أبنائها غير الموسَّعين unexpanded children. اجعل مسافة الحرف الأصلي source vertex على 0، ثمّ حدّث الأسلاف وفقًا لذلك. احسب المسافات بنظام العدّ من الأساس b أو base b، وعند زيارة عقدة في المستوى k للمرة الأولى، ضع أبناءها في مجموعات أو سلَّات buckets مشتركة بين جميع العقد من المستوى k. وخذ بالحسبان أوّل b سلّة وحسب في كل مرة تزور فيها عقدة، وَزُر كلّ واحدة منها ثمّ أزلها، ثمّ حدّث مسافة العقدة الحالية، وَأعِد ربط العقدة الحالية بأصلها باستخدام المسافة الجديدة وانتظر الزيارة القادمة للسلات التالية. عند زيارة ورقة leaf، تكون المسافة الحالية هي المسافة النهائية للحرف. وسِّع جميع الأضلاع المنطلقة منه في المخطط الأصلي، ثمّ حدّث المسافات وفقًا لذلك. زر العقدة الجذرية (المخطط كاملًا) بشكل متكرر إلى أن تصل إلى الوجهة المقصودة. تعتمد هذه الخوارزمية على حقيقة أنّه لا يمكن أن يوجد ضلع ذا طول أقل من l بين مكوّنيْن متصليْن في غابة متفرّعة ذات حدّ طولي يساوي length limitation، لذلك، يمكنك حصر تركيزك على مكوّن واحد متصل بدءًا من مسافة x إلى أن تصل إلى المسافة x + l. ستزور بعض الحروف في الطريق قبل زيارة جميع الحروف ذات المسافة الأقصر، لكن ذلك لا يهم بما أنّنا نعلم أنّه لن يكون هناك مسار أقصر إلى هنا من تلك الحروف. اجتياز المخططات Graph Traversals هناك العديد من الخوارزميات للبحث في المخططات، سنستعرض إحداها فيما يلي، وهي خوارزمية البحث العميق أولا. تنفذ الشيفرة التالية هذه الخوارزمية، إذ تنشئ دالة تأخذ فهرس العقدة الحالي كوسيط، وقائمة التجاور (مخزّنة في متجهة من المتجهات)، ومتجهة منطقية vector of boolean لتعقّب العقدة التي تمت زيارتها، انظر: void dfs(int node, vector<vector<int>>* graph, vector<bool>* visited) { // التحقّق مما إذا كانت العقدة مُزارة سلفا if((*visited)[node]) return; // set as visited to avoid visiting the same node twice (*visited)[node] = true; // نفّذ بعض الإجراءات هنا cout << node; // اجتياز العقد المتجاورة عبر البحث العميق أولا for(int i = 0; i < (*graph)[node].size(); ++i) dfs((*graph)[node][i], graph, visited); } ترجمة -بتصرّف- للفصلين 9 و10 من كتاب Algorithms Notes for Professionals اقرأ أيضًا المقالة السابقة: الأشجار Trees في الخوازرميات مدخل إلى الخوارزميات دليل شامل عن تحليل تعقيد الخوارزمية النسخة الكاملة من كتاب مدخل إلى الذكاء الاصطناعي وتعلم الآلة1 نقطة

























.png.603fdf87571e0cdfaa8f60e5abf75744.png)