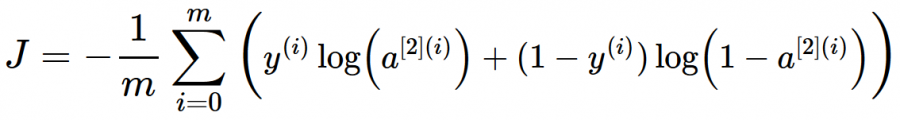لوحة المتصدرين

يقول دونالد كنوث Donald Knuth لا غنى عن الدوال في لغة جافاسكربت، إذ نستخدمها في هيكلة البرامج الكبيرة لتقليل التكرار، ولربط البرامج الفرعية بأسماء، وكذا لعزل تلك البرامج الفرعية عن بعضها، ولعل أبرز تطبيق على الدوال هو إدخال مصطلحات جديدة في اللغة. حيث يمكن إدخال أيّ مصطلح إلى لغة البرمجة من أيّ مبرمج يعمل بها، وذلك على عكس لغات البشر المنطوقة التي يصعب إدخال مصطلحات إليها، إلا بعد مراجعات واعتمادات من مجامع اللغة. وفي الواقع المشاهد، يُعَدّ إدخال المصطلحات إلى اللغة على أساس دوال، ضرورةً حتميةً لاستخدامها في البرمجة وإنشاء برامج للسوق. فمثلًا، تحتوي اللغة الإنجليزية -وهي المكتوب بحروفها أوامر لغات البرمجة-، على نصف مليون كلمة تقريبًا، وقد لا يعلم المتحدث الأصلي لها إلا بـ 20 ألف كلمة منها فقط، وقَلَّ ما تجد لغةً من لغات البرمجة التي يصل عدد أوامرها إلى عشرين ألفًا. وعليه، ستكون المصطلحات المتوفرة فيها دقيقة المعنى للغاية، وبالتالي فهي جامدة وغير مرنة، ولهذا نحتاج إلى إدخال مصطلحات جديدة على هيئة دوال، وذلك بحسب حاجة كل مشروع أو برنامج. تعريف الدالة الدالة هي رابطة منتظمة، حيث تكون قيمة هذه الرابطة هي الدالة نفسها، إذ تُعرِّف الشيفرة التالية مثلًا، الثابت square لتشير إلى دالة تنتج مربع أي عدد مُعطَى: const square = function(x) { return x * x; }; console.log(square(12)); // → 144 وتُنشأ الدالة بتعبير يبدأ بكلمة function المفتاحية، كما يكون للدوال مجموعة معامِلات parameters -معامِل وحيد هو x حسب المثال السابق-، ومتن body لاحتواء التعليمات التي يجب تنفيذها عند استدعاء الدالة، كما يُغلَّف متن الدالة بقوسين معقوصين حتى ولو لم يكن فيه إلا تعليمة واحدة. كذلك يجوز للدالة أن يكون لها عدة معامِلات، أو لا يكون لها أيّ معامِل، ففي المثال التالي، لا تحتوي دالة makenoise على أيّ معاملات، بينما تحتوي power على معاملين اثنين: const makeNoise = function() { console.log("Pling!"); }; makeNoise(); // → Pling! const power = function(base, exponent) { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; }; console.log(power(2, 10)); // → 1024 وتنتج بعض الدوال قيمًا، مثل: دالتي power، وsquare، ولكن هذا ليس قاعدة، إذ لا تعطي بعض الدوال الأخرى قيمةً، مثل دالة makenoise، ونتيجتها الوحيدة هي أثر جانبي side effect. تحدِّد تعليمة return القيمة التي تعيدها الدالة، فحين تمر بُنية تحكُّم control -مثل التعليمات الشرطية- على تعليمة مشابهة لهذه، فستقفز مباشرةً من الدالة الحالية، وتعطي القيمة المعادة إلى الشيفرة التي استدعت الدالة. وإن لم يتبع كلمة return المفتاحية أيّ تعبير، فستعيد الدالة قيمة غير معرفة undefined، كما تعيد الدوال التي ليس فيها تعليمة return قيمة غير معرفة undefined، مثل دالة makenoise. تتصرف معامِلات الدالة على أساس الرابطات المنتظمة regular bindings، غير أنّه يحدِّد مستدعي الدالة قيمتها الأولية، وليس الشيفرة التي بداخل الدالة. الرابطات Bindings والنطاقات Scopes نطاق الرابطة في البرنامج هو الجزء الذي تكون الرابطة ظاهرةً فيه، حيث كل رابطة لها نطاق. وإذا عرَّفنا الرابطة خارج دالة أو كتلة شيفرات، فيكون نطاق هذه الرابطة البرنامج كاملًا، ويمكنك الإشارة إلى مثل تلك الرابطات أينما تشاء، وتسمى رابطات عامة Global Bindings؛ أما الرابطات المنشأة لمعامِلات الدالة، أو المصرح عنها داخل دالة ما، فيمكن الإشارة إليها داخل تلك الدالة فقط، وعليه تسمّى رابطات محلية Local bindings، وتُنشأ نسخ جديدة من تلك الرابطات في كل مرة تُستدعَى الدالة فيها، وذلك يوفر نوعًا من العزل بين الدوال بما أنّ كل دالة تتصرف في عالمها الخاص -بيئتها المحلية-، وييسّر فهم المراد منها دون الحاجة إلى العلم بكل ما في البيئة العامة. كما تكون الرابطات المصرح عنها باستخدام let، وconst رابطات محلية لكتلة الشيفرة التي صُرح عن تلك الرابطات فيها، فإن أنشأت أحد تلك الرابطات داخل حلقة تكرارية، فلن تتمكن الشيفرات الموجودة قبل هذه الحلقة وبعدها، من رؤية تلك الرابطة. ولم يُسمح إنشاء نطاقات جديدة لغير الدوال في إصدارات جافاسكربت قبل 2015، لذا كانت الرابطات التي أُنشِئت باستخدام كلمة var المفتاحية، مرئيةً في كل الدالة التي تظهر فيها هذه الرابطات، أو في النطاق العام إن لم تكن داخل دالة ما. كما في المثال التالي: let x = 10; if (true) { let y = 20; var z = 30; console.log(x + y + z); // → 60 } // y is not visible here console.log(x + z); // → 40 يستطيع كل نطاق البحث في النطاق الذي يحيط به، لذا تكون x ظاهرة داخل كتلة الشيفرة في المثال السابق مع استثناء وجود عدة رابطات بالاسم نفسه، ففي تلك الحالة لا تستطيع الشيفرة إلا رؤية الأقرب لها، كما في المثال التالي، حيث تشير الشيفرة داخل دالة halve إلى n الخاصة بها وليس إلى n العامة: const halve = function(n) { return n / 2; }; let n = 10; console.log(halve(100)); // → 50 console.log(n); // → 10 النطاق المتشعب نستطيع إنشاء كتل شيفرات ودوال داخل كتل ودوال أخرى ليصبح لدينا عدة مستويات من المحلية، فمثلًا، تخرج الدالة التالية المكونات المطلوبة لصنع مقدار من الحمُّص، وتحتوي على دالة أخرى داخلها، أي كما يأتي: const hummus = function(factor) { const ingredient = function(amount, unit, name) { let ingredientAmount = amount * factor; if (ingredientAmount > 1) { unit += "s"; } console.log(`${ingredientAmount} ${unit} ${name}`); }; ingredient(1, "can", "chickpeas"); ingredient(0.25, "cup", "tahini"); ingredient(0.25, "cup", "lemon juice"); ingredient(1, "clove", "garlic"); ingredient(2, "tablespoon", "olive oil"); ingredient(0.5, "teaspoon", "cumin"); }; تستطيع شيفرة الدالة ingredient أن ترى رابطة factor من الدالة الخارجية، على عكس رابطتيها المحليتين الغير مرئيتين من الدالة الخارجية، وهما: unit، وingredientAmount. ويُحدِّد مكان كتلة الشيفرة في البرنامج الرابطات التي ستكون مرئيةً داخل تلك الكتلة، حيث يستطيع النطاق المحلي رؤية جميع النطاقات المحلية التي تحتويه، كما تستطيع جميع النطاقات رؤية النطاق العام، ويُسمّى هذا المنظور لمرئية الرابطات، المراقبة المُعجَمية Lexical Scoping. الدوال على أساس قيم تتصرف رابطة الدالة عادةً على أساس اسم لجزء بعينه من البرنامج، وتُعرَّف هذه الرابطة مرةً واحدةً ولا تتغير بعدها، ويسهّل علينا هذا، الوقوع في الخلط بين اسم الدالة والدالة نفسها، غير أنّ الاثنين مختلفان عن بعضهما، إذ تستطيع قيمة الدالة فعل كل ما يمكن للقيم الأخرى فعله، كما تستطيع استخدامها في تعبيرات عشوائية، وتخزينها في رابطة جديدة، وتمريرها كوسيط لدالة، وهكذا. وذلك إضافةً إلى إمكانية استدعاء تلك القيمة بلا شك. وبالمثل، لا تزال الرابطة التي تحمل الدالة مجرد رابطة منتظمة regular bindung، كما يمكن تعيين قيمة جديدة لها إذا لم تكن ثابتة constant، كما في المثال الآتي: let launchMissiles = function() { missileSystem.launch("now"); }; if (safeMode) { launchMissiles = function() {/* لا تفعل شيئًا */}; } وسنناقش في المقال الخامس بعض الأمور الشيقة التي يمكن فعلها بتمرير قيم الدالة إلى دوال أخرى. مفهوم التصريح توجد طريقة أقصر لإنشاء رابطة للدالة، حيث تُستخدم كلمة function المفتاحية في بداية التعليمة، أي كما يلي: function square(x) { return x * x; } ويسمى هذا بتصريح الدالة function declaration، فتعرِّف التعليمة الرابطة "square" وتوجهها إلى الدالة المعطاة، وذلك أسهل قليلًا في الكتابة، ولا يتطلب فاصلة منقوطة بعد الدالة، لكن قد يكون هذا الأسلوب من التصريح عن الدوال خدّاعًا: console.log("يقول لنا المستقبل", future()); function future() { return "لن تكون هناك سيارات تطير"; } وعلى الرغم من أن الدالة معرَّفة أسفل الشيفرة التي تستخدمها، إلا أنها صالحة وتعمل بكفاءة، وذلك لأن تصريح الدوال ليس جزءًا من مخطط السير العادي من الأعلى إلى الأسفل، بل يتحرك إلى قمة نطاقه، ويكون متاحًا للاستخدام من قِبَل جميع الشيفرات الموجودة في ذلك النطاق، ويفيدنا هذا أمر أحيانًا لأنه يوفر حرية ترتيب الشيفرة ترتيبًا منطقيًا ومفيدًا، دون القلق بشأن الحاجة إلى تعريف كل الدوال قبل استخدامها. الدوال السهمية Arrow Functions لدينا مفهوم ثالث للتصريح عن الدوال، وقد يبدو مختلفًا عن البقية، حيث يستخدِم سهمًا مكتوبًا في صورة إشارة التساوي ومحرف "أكبر من"، أي على الصورة (‎=>‎)، لهذا انتبه من الخلط بينها وبين محرف "أكبر من أو يساوي"، الذي يُكتب على الصورة (‎>=‎)، ويوضح المثال التالي هذا المفهوم: const power = (base, exponent) => { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; }; يأتي السهم بعد قائمة المعامِلات ويُتبع بمتن الدالة، ويكون على صورة: "هذا الدخل (المعامِلات) يُنتِج هذا الخرج (المتن)"، وحين يكون لدينا اسم معامِل واحد، فيمكنك إهمال الأقواس المحيطة بقائمة المعامِلات، وإن كان المتن تعبيرًا واحدًا بدلًا من كتلة بين قوسين، فستعيد الدالة ذلك التعبير، وعليه ينفذ التعريفين التاليين لـ square، الشيء نفسه: const square1 = (x) => { return x * x; }; const square2 = x => x * x; وعندما تكون الدالة السهمية بدون معامِلات على الإطلاق، فستكون قائمة معامِلاتها مجرد قوسين فارغين، أي كما في المثال التالي: const horn = () => { console.log("Toot"); }; ليس ثمة سبب لوجود الدوال السهمية وتعبيرات function معًا في اللغة، إذ يملكان الوظيفة نفسها بصرف النظر عن التفاصيل الصغيرة، وسنتحدث عن ذلك في المقال السادس، كما لم تُضَف الدوال السهمية إلا في عام 2015، وذلك من أجل السماح بكتابة تعبيرات دوال صغيرة بأسلوب قليل الصياغة، حيث سنستخدمها كثيرًا في المقال الخامس. مكدس الاستدعاء The call stack قد تبدو طريقة تدفُق التحكم خلال الدوال متداخلة قليلا، انظر المثال التالي للتوضيح، حيث ينفذ بعض الاستدعاءات من الدوال المعطاة: function greet(who) { console.log("Hello " + who); } greet("Harry"); console.log("Bye"); وعند تشغيل البرنامج السابق فإن مخطط سيره يكون كالتالي: عند استدعاء greet، يقفز التحكم إلى بداية تلك الدالة (السطر الثاني في الشيفرة)، وتستدَعي بدورها console.log التي ينتقل التحكم إليها لتُنفّذ مهمتها، ثم تعود إلى المكان الذي استدعاها، وهو السطر الرابع. ثم يستدعي السطر الذي يليه، أي console.log مرةً أخرى، ويصل البرنامج إلى نهايته بعد إعادة ذلك. وإذا أردنا تمثيل مخطط تدفق التحكم لفظيًا، فسيكون كالتالي: خارج الدالة في greet في console.log في greet خارج الدالة في console.log خارج الدالة ونظرًا لوجوب قفز الدالة إلى المكان الذي استدعاها، فلابد للحاسوب من تذكُّر السياق الذي حدث منه الاستدعاء، ففي إحدى الحالات أعلاه، كان على console.log العودة إلى دالة greet عند انتهاء تنفيذها، بينما تعود إلى نهاية البرنامج في الحالة الأخرى. يسمى المكان الذي يخزن فيه الحاسوب هذا السياق، بمكدس الاستدعاء call stack، ويُخزَّن السياق الحالي في قمة ذلك المكدس في كل مرة تُستدعى دالة، كما تزيل السياق الأعلى من المكدس، وتستخدمه لمتابعة التنفيذ عندما تعود الدالة.، حيث يحتاج هذا المكدس إلى مساحة في ذاكرة الحاسوب، وبما أنّ تلك المساحة محدودة، فقد يعطيك الحاسوب رسالة فشل، مثل: عدم وجود ذاكرة كافية في المكدس "out of stack space"، أو تكرارات تفوق الحد المسموح به "too much recursion". حيث لدينا المثال الآتي: function chicken() { return egg(); } function egg() { return chicken(); } console.log(chicken() + " came first."); // → ?? إذ توضح الشيفرة السابقة هذا الأمر بسؤال الحاسوب أسئلة صعبة، تجعله يتنقّل بين الدالتين ذهابًا وإيابًا إلى ما لا نهاية، وفي حالة المكدس اللانهائي هذه، فستنفذ ذاكرة الحاسوب المتاحة، أو ستطيح بالمكدس blow the stack. الوسائط الاختيارية Optional arguments انظر الشيفرة التالية: function square(x) { return x * x; } console.log(square(4, true, "hedgehog")); // → 16 تسمح لغة جافاسكربت بتنفيذ الشيفرة السابقة دون أدنى مشكلة، ورغم أننا عرَّفنا فيها square بمعامِل واحد فقط، ثم استدعيناها بثلاثة معامِلات، فقد تجاهلت الوسائط الزائدة، وحسبت مربع الوسيط الأول فقط. وتستنتج من هذا أن جافاسكربت لديها سعة -إن صح التعبير- في شأن الوسائط التي تمررها إلى الدالة، فإن مررت وسائط أكثر من اللازم، فستُتجاهل الزيادة، أما إن مرّرت وسائط أقل من المطلوب، فتُسنَد المعامِلات المفقودة إلى القيمة undefined. وسيّئة ذلك أنك قد تُمرِّر عدد خاطئ من الوسائط، ولن تعرف بذلك، ولن يخبرك أحد ولا حتى جافاسكربت نفسها، أما حسنته فيمكن استخدام هذا السلوك للسماح لدالة أن تُستدعى مع عدد مختلف من الوسائط. انظر المثال التالي حيث تحاول دالة minus محاكاة معامِل - من خلال وسيط واحد أو وسيطين: function minus(a, b) { if (b === undefined) return -a; else return a - b; } console.log(minus(10)); // → -10 console.log(minus(10, 5)); // → 5 وإذا كتبنا عامل = بعد معامِل ما، ثم أتبعنا ذلك بتعبير، فستحل قيمة التعبير محل الوسيط إذا لم يكن معطى مسبقًا، إذ تجعل دالة الأس power مثلًا، وسيطها الثاني اختياريًا، فإن لم تعطها أنت ذلك الوسيط أو تمرر قيمة undefined، فسيتغير تلقائيًا إلى 2، وستتصرف الدالة مثل دالة التربيع square بالضبط، كما يأتي: function power(base, exponent = 2) { let result = 1; for (let count = 0; count < exponent; count++) { result *= base; } return result; } console.log(power(4)); // → 16 console.log(power(2, 6)); // → 64 سننظر في المقال التالي إلى طريقة يحصل بها متن الدالة على جميع الوسائط الممررة، ويفيدنا هذا في السماح للدالة بقبول أي عدد من الوسائط، كما في console.log، إذ تُخرج كل القيم المعطاة إليها، أي: console.log("C", "O", 2); // → C O 2 التغليف Closure إذا قلنا أننا نستطيع معاملة الدوال مثل قيم، وأنه يعاد إنشاء الرابطات المحلية في كل مرة تُستدعى فيها الدالة، فإننا نتساءل هنا عما يحدث لتلك الرابطات حين يصير الاستدعاء الذي أنشأها غير نشط؟ توضح الشيفرة التالية مثالًا على هذا، فهي تعرِّف دالة wrapValue، والتي تنشئ رابطةً محليةً، ثم تعيد دالةً تصل إلى تلك الرابطة وتعيدها. انظر: function wrapValue(n) { let local = n; return () => local; } let wrap1 = wrapValue(1); let wrap2 = wrapValue(2); console.log(wrap1()); // → 1 console.log(wrap2()); // → 2 يُعَدّ هذا الأسلوب جائزًا ومسموحًا به في جافاسكربت، ولا يزال بإمكانك الوصول إلى كلا النسختين، حيث يوضح ذلك المثال حقيقة أنّ الرابطات المحلية تُنشَأ من جديد في كل استدعاء، وأنّ الاستدعاءات المختلفة لا تدمر رابطات بعضها البعض. وتسمّى تلك الخاصية بالمغلِّف closure، أي خاصية القدرة على الإشارة إلى نسخة بعينها من رابطة محلية في نطاق محيط enclosing scope، وتسمى الدالة التي تشير إلى رابطات من نطاقات محلية حولها، بالمغلف closure. يحررك هذا السلوك من القلق بشأن دورة حياة تلك الرابطات، ويتيح لك استخدام قيم الدوال بطرق جديدة، فيمكِّننا تغيير بسيط، من قلب المثال السابق إلى طريقة لإنشاء دوال تضاعِف بقيمة عشوائية، أي كما يلي: function multiplier(factor) { return number => number * factor; } let twice = multiplier(2); console.log(twice(5)); // → 10 وبما أنّ المعامِل نفسه يُعَدّ رابطةً محليةً، فلم نعد بحاجة إلى الرابطة الصريحة local من دالة wrapValue السابقة. ويحتاج التفكير في برامج مثل هذا إلى بعض التمرس، والنموذج الذهني المعين على هذا هو التفكير في قيم الدالة على أنها تحتوي شيفرة المتن وبيئتها التي أُنشئَت فيها، وحين تُستدعى الدالة، يرى متن الدالة البيئة التي أنشئت فيها وليس البيئة التي استدعيَت فيها. وفي المثال السابق، تُستدعى الدالة multiplier، وتُنشئ بيئة يكون فيها المعامل factor مقيدًا بـ 2، وتتذكر قيمة الدالة التي تعيدها، وتكون مخزنة في twice، هذه البيئة، لذا حين تُستدعى فستضاعف وسيطها بمقدار 2. التعاود Recursion تستطيع الدالة استدعاء نفسها طالما أنها لا تكثر من ذلك إلى الحد الذي يطفح المكدس، وتسمى هذه الدالة المستدعية نفسها باسم العودية recursive، حيث يسمح التعاود لبعض الدوال بأن تُكتب في صور مختلفة كما في المثال التالي، إذ نرى استخدامًا مختلفًا لدالة الأس power: function power(base, exponent) { if (exponent == 0) { return 1; } else { return base * power(base, exponent - 1); } } console.log(power(2, 3)); // → 8 وهذا قريب من الطريقة التي يُعرَّف بها الأس عند الرياضيين، ويصف الفكرة أفضل من الصورة التكرارية looping، إذ تستدعي الدالة نفسها عدة مرات مع أسس مختلفة، لتحقيق عمليات الضرب المتكررة. ولكن ثمة مشكلة في هذا النموذج، إذ هو أبطأ بثلاث مرات من الصورة التكرارية في تطبيقات جافاسكربت، فالمرور على حلقة تكرارية أيسر، وأقل تكلفةً من استدعاء دالة عدة مرات. وهذه المسألة، أي مسألة السرعة مقابل الأناقة، لَمعضلة فريدة بين ما يناسب الإنسان وما يناسب الآلة، فلا شك أننا نستطيع زيادة سرعة البرنامج إذا زدنا حجمه وتعقيده، وإنما يقع على المبرمج تقدير كل موقف ليوازن بين هذا وذاك. وإذا عدنا إلى حالة دالة الأس السابقة power، فأسلوب التكرار looping وهو المنظور غير الأنيق هنا، هو أبسط وأيسر في القراءة، وليس من المنطق استبدال النسخة التعاودية recursive به وإحلالها محله، لكن اعلم أنّ اختيار الأسهل، والأرخص، والأقل تكلفةً في المال والموارد الأخرى، ليس القاعدة في البرمجة، ولا يجب أن يكون كذلك، فقد يُعرض لنا موقف نتخلى فيه عن هذه الكفاءة من السهولة والسرعة في سبيل جعل البرنامج بسيطًا وواضحًا، وقد يكون فرط التفكير في الكفاءة مشتتًا لك عن المطلوب من البرنامج في الأصل، فهذا عامل آخر يعطل تصميمه، وبحسب المرء تعقيد البرنامج ومطلوب العميل منه، فلا داعي لإضافة عناصر جديدة تزيد القلق إلى حد العجز عن التنفيذ وإتمام العمل. لهذا أنصحك بمباشرة أول كتابتك للبرنامج بكتابة شيفرة صحيحة عاملة وسهلة الفهم، وهذا رأيي في ما يجب عليك وضعه كهدف نصب عينيك، وإن أردت تسريع البرنامج فتستطيع ذلك لاحقًا بقياس أدائه ثم تحسين سرعته إن دعت الحاجة، وإن كان القلق بشأن بطء البرنامج غالبًا ليس في محله بما أن أغلب الشيفرات لا تُنفَّذ بالقدر الذي يجعلها تأخذ وقتًا ملحوظًا. فقد تجد أحيانًا مشكلات يكون حلها أسهل باستخدام التعاود عوضًا عن التكرار، وهي المشاكل التي تتطلب استكشاف عدة فروع أو معالجتها، إذ قد تحتوي تلك الفروع بدورها على فروع أخرى، وهكذا تجد أنّ التكرار قد يكون أقل كفاءةً من التعاود أحيانًا! يمكنك النظر إلى الأحجية التالية كمثال على هذا، فإذا بدأنا من العدد 1 وأضفنا 5 أو ضربنا في 3 باستمرار ، فسينتج لدينا مجموعة لا نهائية من الأعداد. كيف تكتب دالةً نعطيها عددًا فتحاول إيجاد تسلسل عمليات الجمع والضرب التي تنتج هذا العدد؟ إرشاد: يمكن التوصل إلى العدد 13 بضرب 1 في 3، ثم إضافة 5 مرتين، في حين أننا لن نستطيع الوصول إلى العدد 15 مطلقًا. انظر الحل الآن بأسلوب التعاود: function findSolution(target) { function find(current, history) { if (current == target) { return history; } else if (current > target) { return null; } else { return find(current + 5, `(${history} + 5)`) || find(current * 3, `(${history} * 3)`); } } return find(1, "1"); } console.log(findSolution(24)); // → (((1 * 3) + 5) * 3) لاحظ أنّ هذا البرنامج لا يزعج نفسه بالبحث عن أقصر تسلسل من العمليات، بل أي تسلسل يحقق المراد وحسب، ولأن هذا البرنامج مثال رائع على أسلوب التفكير التعاودي، فسأعيد شرحه مفصلًا إن لم تستوعب منطقه بمجرد النظر. تنفذ دالة find الداخلية التعاود الحقيقي، فتأخذ وسيطين: العدد الحالي، وسلسلة نصية string لتسجل كيف وصلنا إلى هذا العدد، فإن وجدت حلًا، فستعيد سلسلةً نصيةً توضح كيفية الوصول إلى الهدف؛ أما إن لم تجد حلا بالبدء من هذا العدد، فستعيد null. ولتحقيق ذلك، تنفِّذ الدالة أحد ثلاثة إجراءات: يُعاد العدد الحالي إن كان هو العدد الهدف، حيث يُعَد السجل الحالي طريقة للوصول إليه. تُعاد null إن كان العدد الحالي أكبر من الهدف، فليس من المنطق أن نبحث في هذا الفرع، حيث ستجعل عملية الإضافة أو الضرب، العدد أكبر مما هو عليه. تُعاد النتيجة إن كنا لا نزال أقل من العدد الهدف، فتحاول الدالة كلا الطريقتين اللتين تبدءان من العدد الحالي باستدعاء نفسها مرتين، واحدة للإضافة وأخرى للضرب، وتُعاد نتيجة الاستدعاء الأول إن كان أي شيء غير null، وإلا فيُعاد الاستدعاء الثاني بغض النظر عن إخراجها لسلسلة نصية أم null. ولفهم كيفية إخراج هذه الدالة للأثر الذي نريده، دعنا ننظر في الاستدعاءات التي تُجرى على دالة find، عند البحث عن حل للعدد 13: find(1, "1") find(6, "(1 + 5)") find(11, "((1 + 5) + 5)") find(16, "(((1 + 5) + 5) + 5)") too big find(33, "(((1 + 5) + 5) * 3)") too big find(18, "((1 + 5) * 3)") too big find(3, "(1 * 3)") find(8, "((1 * 3) + 5)") find(13, "(((1 * 3) + 5) + 5)") found! لاحظ أنّ الإزاحة في المثال السابق توضح عمق مكدس الاستدعاء. حيث تستدعي find في أول استدعاء لها باستدعاء نفسها للبحث عن حل يبدأ بـ (1+5)، وسيتعاود هذا الاستدعاء للبحث في كل حل ينتج عددًا أقل أو يساوي العدد الهدف. وتعيد null إلى الاستدعاء الأول بما أنها لن تجد ما يطابق الهدف، وهنا يتدخل عامل || ليتسبب في الاستدعاء الذي يبحث في (1*3)، ويكون هذا البحث هو أول استدعاء تعاودي داخل استدعاء تعاودي آخَر يصيب العدد الهدف. ويعيد آخر استدعاء فرعي سلسلة نصية، وتُمرر هذه السلسلة من قبل عامليْ || في الاستدعاء البيني intermediate call، مما يعيد لنا الحل في النهاية. الدوال النامية Growing Functions لدينا في البرمجة طريقتين لإدخال الدوال في البرامج، أولاهما أن تجد نفسك تكرر كتابة شيفرة بعينها عدة مرات، وهو أمر لا شك أنك لا تريد فعله، فيزيد وجود شيفرات كثيرة من احتمال ورود أخطاء أكثر في البرنامج، ومن الإرهاق المصاحب في البحث عنها، ووقتًا أطول في قراءة الشيفرة منك ومن غيرك ممن يحاول فهم برنامجك لتعديله أو للبناء عليه، لذا عليك أخذ تلك الشيفرة المتكررة وتسميها باسم يليق بها ويعجبك، ثم تضعها في دالة. أما الطريقة الثانية فهي حين تحتاج إلى بعض الوظائف التي لم تكتبها بعد، ويبدو أنها تستحق دالة خاصة بها، فتبدأ بتسمية هذه الدالة، ثم تشرع في كتابة متنها، وقد تبدأ في كتابة التعليمات البرمجية التي تستخدم الدالة قبل تعريف الدالةَ نفسها. واعلم أنّ مقياس وضوح المفهوم الذي تريد وضعه في هذه الدالة، هو مدى سهولة العثور على اسم مناسب للدالة! فكلما كان هدف الدالة واضحًا ومحددًا، سهل عليك تسميتها. ولنقل أنك تريد كتابة برنامج لطباعة عددين: عدد الأبقار، وعدد الدجاج في مزرعة، مع إتباع العدد بكلمة بقرة، وكلمة دجاجة بعده، ووضع أصفار قبل كلا العددين بحيث يكون طولهما دائمًا ثلاثة خانات، فهذا يتطلب دالةً من وسيطين، وهما: عدد الأبقار، وعدد الدجاج. 007 Cows 011 Chickens وهذا يتطلب دالة من وسيطين، هما: عدد الأبقار، وعدد الدجاج. function printFarmInventory(cows, chickens) { let cowString = String(cows); while (cowString.length < 3) { cowString = "0" + cowString; } console.log(`${cowString} Cows`); let chickenString = String(chickens); while (chickenString.length < 3) { chickenString = "0" + chickenString; } console.log(`${chickenString} Chickens`); } printFarmInventory(7, 11); إذا كتبنا length. بعد تعبير نصي، فسنحصل على طول هذا التعبير، أو هذه السلسلة النصية، وعليه ستضيف حلقات while التكرارية أصفارًا قبل سلاسل الأعداد النصية، لتكون ثلاثة محارف على الأقل. وهكذا، فقد تمت مهمتنا! ولكن لنفرض أنّ صاحبة المزرعة قد اتصلت بنا قبيل إرسال البرنامج إليها، وأخبرتنا بإضافة اسطبل إلى مزرعتها، حيث استجلبت خيولًا، وطلبت إمكانية طباعة البرنامج لبيانات الخيول أيضًا. هنا تكون الإجابة أننا نستطيع، لكن خطر لنا خاطر بينما نحن نوشك على نسخ هذه الأسطر الأربعة، ونلصقها مرةً أخرى، إذ لا بد من وجود طريقة أفضل، أي كما يأتي: function printZeroPaddedWithLabel(number, label) { let numberString = String(number); while (numberString.length < 3) { numberString = "0" + numberString; } console.log(`${numberString} ${label}`); } function printFarmInventory(cows, chickens, horses) { printZeroPaddedWithLabel(cows, "Cows"); printZeroPaddedWithLabel(chickens, "Chickens"); printZeroPaddedWithLabel(horses, "Horses"); } printFarmInventory(7, 11, 3); وهنا نجحت الشيفرة، غير أنّ اسم printZeroPaddedWithLabel محرج نوعًا ما، إذ يجمع في وظيفة واحدة، بين كل من: الطباعة، وإضافة الأصفار، وإضافة العنوان label، لذا بدلًا من إلغاء الجزء المكرر من البرنامج. دعنا نختر مفهومًا واحدًا فقط: function zeroPad(number, width) { let string = String(number); while (string.length < width) { string = "0" + string; } return string; } function printFarmInventory(cows, chickens, horses) { console.log(`${zeroPad(cows, 3)} Cows`); console.log(`${zeroPad(chickens, 3)} Chickens`); console.log(`${zeroPad(horses, 3)} Horses`); } printFarmInventory(7, 16, 3); حيث تسهل الدالة ذات الاسم الجميل والواضح مثل zeroPad، على الشخص الذي يقرأ الشيفرة معرفة ما تفعله، وهي مفيدة في مواقف أكثر من هذا البرنامج خاصة، إذ تستطيع استخدامها لطباعة جداول منسقة من الأعداد. لكن إلى أي حد يجب أن تكون الدالة التي تكتبها ذكية، بل إلى أي حد يجب أن تكون متعددة الاستخدامات؟ اعلم أنك تستطيع عمليًا كتابة أي شيء بدءًا من دالة بسيطة للغاية، حيث تحشو عددًا ليكون بطول ثلاثة محارف، إلى نظام تنسيق الأعداد المعمم والمعقد، والذي يتعامل مع الأعداد الكسرية، والأعداد السالبة، ومحاذاة الفواصل العشرية، والحشو بمحارف مختلفة، وغير ذلك. والقاعدة هنا، هي ألا تجعل الدالة تزيد في وظيفتها عن الحاجة، إلا إذا تأكدت يقينًا من حاجتك إلى تلك الوظيفة الزائدة، فقد يكون من المغري كتابة "أُطر عمل" frameworks عامة لكل جزء من الوظائف التي تصادفها، لكنا نهيب بك ألا تستجيب لهذه الرغبة، إذ لن تنجز أيّ عمل حقيقي لأيّ عميل ولا لنفسك حتى، وإنما ستكتب شيفرات لن تستخدمها أبدًا. الدوال والآثار الجانبية يمكن تقسيم الدوال إلى تلك التي تُستدعَى لآثارها الجانبية side effects، وتلك التي تُستدعَى لقيمتها المعادة -رغم أنه قد يكون للدالة آثار جانبية، وقيم معادة في الوقت نفسه-، فالدالة الأولى هي دالة مساعدة في مثال المزرعة السابق، حيث تُستدعَى printZeroPaddedWithLabel لأثرها الجانبي، فتطبع سطرًا؛ أما النسخة الثانية zeroPad، فتُستدعى لقيمتها المعادة. ولا شك أنّ الحالة الثانية مفيدة أكثر من الأولى، فتكون الدوال التي تنشئ قيمًا، أسهل في إدخالها وتشكيلها في صور جديدة عن تلك التي تنتج آثارًا جانبية مباشرة. ولدينا من ناحية أخرى، دالةً تسمى بالدالة النقية pure function، وهي نوع خاص من الدوال المنتجة للقيم، حيث لا تحتوي على آثار جانبية، كما لا تعتمد على الآثار الجانبية من شيفرة أخرى، فمثلًا، لا تقرأ هذه الدوال الرابطات العامة global bindings التي قد تتغير قيمتها. ولهذا النوع من الدوال خاصية فريدة، إذ تنتج القيمة نفسها إن استُدعيَت بالوسائط نفسها، ولا تفعل أي شيء آخر، وإضافةً إلى ما سبق، ولا يتغير معنى الشيفرة إن أزلنا استدعاء الدالة ووضعنا مكانه القيمة التي ستعيدها. وإن حدث وشككت في عمل دالة نقية، فيمكنك اختبارها ببساطة عن طريق استدعائها، واعلم أنها إذا عملت في هذا السياق، فستعمل في أي سياق آخر، إذ تحتاج الدوال غير النقية إلى دعامات أخرى لاختبارها. لكن مع هذا، فلا داعي للاستياء عند كتابة دوال غير نقية، أو تنفيذ عمليات تطهير لحذفها من شيفراتك، فقد تكون الآثار الجانبية مفيدة، وهذا يحدث في الغالب من حالات البرمجة. فمثلًا، لا توجد طريقة لكتابة نسخة نقية من console.log، ونحن نحتاج هذه الدالة أيما احتياج، كما سترى أثناء تمرسك في جافاسكربت لاحقًا، كذلك تسهل الآثار الجانبية من التعبير عن بعض العمليات بطريقة فعالة، لذا قد تكون الحاجة للسرعة سببًا لتجنب هذا النقاء في الدوال. خاتمة اطلعنا في هذا المقال على كيفية كتابة الدوال البرمجية التي تحتاجها عند تنفيذ مهمة، أو وظيفة متكررة في برامجك، وذلك باستخدام كلمة function المفتاحية التي تستطيع إنشاء قيمة دالة إذا استُخدمت على أساس تعبير؛ أما إذا استُخدمت على أساس تعليمة، فتكون للإعلان عن رابطة binding، وإعطائها دالة تكون قيمةً لها؛ كما نستطيع إنشاء الدوال أيضًا باستخدام الدوال السهمية. يُعَدّ أحد الجوانب الرئيسية في فهم الدوال هو فهم النطاقات، حيث تنشئ كل كتلة نطاقًا جديدًا، وتكون المعامِلات والرابطات المصرَّح عنها في نطاق معين محلية وغير مرئية من الخارج. كما تتصرف الرابطات المصرَّح عنها بـ var تصرفًا مختلفًا، حيث ينتهي بهم الأمر في أقرب نطاق دالي أو في النطاق العام. واعلم أنّ فصل المهام التي ينفذها برنامجك إلى دوال مختلفة يفيدك في انتفاء الحاجة إلى التكرار الزائد عن الحد، وسترى أنّ الدوال مفيدة في تنظيم البرنامج، إذ تجمع تجميع الشيفرة في أجزاء تنفذ أشياءً محددة. ترجمة -بتصرف- للفصل الثالث من كتاب Elequent Javascript لصاحبه Marijn Haverbeke.

تحدثنا في المقال الرابع عن الكائنات في جافاسكربت، ولدينا في ثقافة البرمجة شيء يسمى بالبرمجة كائنية التوجه، وهي مجموعة تقنيات تستخدم الكائنات والمفاهيم المرتبطة بها مثل مبدأ مركزي لتنظيم البرامج. ورغم عدم وجود إجماع على التعريف الدقيق للبرمجة كائنية التوجه هذه، إلا أنها قد غيرت شكل لغات برمجة كثيرة من حيث تصميمها، بما فيها جافاسكربت، وسنتعرض في هذا المقال للطرق التي يمكن تطبيق أفكار هذا المفهوم في جافاسكربت. التغليف Encapsulation تتلخص فكرة البرمجة كائنية التوجه في تقسيم البرامج إلى أجزاء صغيرة وجعل كل جزء مسؤولًا عن إدارة حالته الخاصة، وهكذا يمكن حفظ المعلومات الخاصة بالأسلوب الذي يعمل به جزء ما من البرنامج داخل ذلك الجزء فقط محليًا، بحيث إذا عمل شخص ما على جزء آخر من البرنامج، فليس عليه معرفة أو إدراك حتى هذه البيانات والمعلومات؛ وإذا تغيرت تلك التفاصيل المحلية، فلن نحتاج سوى إلى تعديل جزء الشيفرة المتعلق بها فقط. ويُطلق على فصل الواجهة عن الاستخدام نفسه أو التطبيق بـالتغليف، وهو فكرة عظيمة. تتفاعل الأجزاء المختلفة من البرامج مع بعضها البعض من خلال واجهات interfaces، وهي مجموعات محدودة من الدوال أو الرابطات bindings التي توفر أداءً مفيدًا في المستويات العليا التجريدية التي تخفي استخدامها الدقيق والمباشر. كما نُمذِجت مثل تلك الأجزاء باستخدام كائنات، وواجهاتها مكونة من مجموعات محددة من التوابع والخصائص، حيث يوجد نوعان من هذه الخصائص، إما عامة عندما تكون جزءًا من الواجهة، أو خاصة يجب ألا يقربها أي شيء خارج الشيفرة. توفر الكثير من اللغات طريقةً للتمييز بين الخصائص العامة والخاصة، وذلك لمنع الشيفرات الخارجية من الوصول إلى الخصائص الخاصة؛ أما جافاسكربت فلا تفعل ما سبق، إذ تتبع أسلوبها البسيط في ذلك حاليًا، ويوجد ثمة أعمال لإضافة ذلك إليها. رغم عدم دعم اللغة لهذه الخاصية في التفرقة، إلا أنّ مبرمجي جافاسكربت يفعلون ذلك من حيث المبدأ، فالواجهة المتاحة موصوفة ومشروحة في التوثيق أو التعليقات، ومن الشائع كذلك وضع شرطة سفلية (_) في بداية أسماء الخصائص للإشارة إلى أنها "خاصة". التوابع Methods التوابع ليست إلا خصائص حاملة لقيم الدوال، انظر المثال التالي لتابع بسيط: let rabbit = {}; rabbit.speak = function(line) { console.log(`The rabbit says '${line}'`); }; rabbit.speak("I'm alive."); // → The rabbit says 'I'm alive.' يُتوقع من التابع فعل شيء بالكائن الذي استدعي له، فحين تُستدعى دالة على أساس تابع -يُبحث عنها على أساس خاصية، ثم تُستدعى مباشرةً كما في حالة object.method()‎-، ستشير الرابطة التي استدعت this في متنها مباشرةً إلى الكائن الذي استُدعي عليه. function speak(line) { console.log(`The ${this.type} rabbit says '${line}'`); } let whiteRabbit = {type: "white", speak}; let hungryRabbit = {type: "hungry", speak}; whiteRabbit.speak("Oh my ears and whiskers, " + "how late it's getting!"); // → The white rabbit says 'Oh my ears and whiskers, how // late it's getting!' hungryRabbit.speak("I could use a carrot right now."); // → The hungry rabbit says 'I could use a carrot right now.' فكر في this على أساس معامِل إضافي يُمرَّر في صورة مختلف، فإذا أردت تمريره صراحةً، فستستخدِم تابع call الخاص بالدالة والذي يأخذ قيمة this على أساس وسيطها الأول، وتعامِل الوسائط التالية على أساس معامِلات عادية. speak.call(hungryRabbit, "Burp!"); // → The hungry rabbit says 'Burp!' وبما أنّ كل دالة لها رابطة this الخاصة بها، والتي تعتمد قيمتها على الطريقة التي المًستدعاة بها، فلا تستطيع الإشارة إلى this بنطاق مغلِّف في دالة عادية معرَّفة بكلمة function المفتاحية؛ أما الدوال السهمية فتختلف في عدم ارتباط this الخاص بها، لكنها تستطيع رؤية رابطة this للنطاق الذي حولها، وعليه ستستطيع تنفيذ شيء مثل ما في الشيفرة التالية، حيث تشير إلى this مرجعيًا من داخل دالة محلية: function normalize() { console.log(this.coords.map(n => n / this.length)); } normalize.call({coords: [0, 2, 3], length: 5}); // → [0, 0.4, 0.6] فلو كتبنا الوسيط إلى map باستخدام كلمة function المفتاحية، فلن تعمل الشيفرة. الوراثة عبر سلسلة prototype انظر المثال التالي: let empty = {}; console.log(empty.toString); // → function toString(){…} console.log(empty.toString()); // → [object Object] أرأيت كيف سحبنا خاصيةً من كائن فارغ؟! حيث لم نزد على الطريقة التي تعمل بها كائنات جافاسكربت في حفظ البيانات الخاصة، لأن أغلب الكائنات ترث من سلسلة prototype بكل ما تحويه من دوال وخاصيات وكائنات أخرى إضافةً إلى مجموعة خصائصها، وتلك ما هي إلا كائنات أخرى مستخدَمة على أساس مصدر احتياطي fallback للخصائص، فإذا طُلِب من كائن خاصية لا يملكها، فسيُبحث في سلسلة prototype عن تلك الخاصية، ثم في سلاسل prototype الخاصة بكل واحدة فيها على حدى، وهكذا. طيب، ما سلسلة prototype لذاك الكائن الفارغ؟ إنه object.prototype الذي يسبق الكائنات كلها، فإذا قلنا أنّ علاقات سلاسل prototype في جافاسكربت تكوِّن هيكلًا شجريًا، فسيكون جذر تلك الشجرة هو Object.prototype، إذ يوفِّر بعضَ التوابع التي تظهر في جميع الكائنات الأخرى مثل toString الذي يحول الكائن إلى تمثيل نصي string representation. لا تملك العديد من الكائنات Object.prototype مثل نموذجها الأولي (يطلق على سلسلة prototype نموذج أولي مجازًا بوصفه أول نموذج يمثل خاصيات ودوال يرثه الكائن عند إنشائه)، بل يكون لها كائنٌ آخر يوفر مجموعةً مختلفةً من الخصائص الافتراضية. console.log(Object.getPrototypeOf({}) == Object.prototype); // → true console.log(Object.getPrototypeOf(Object.prototype)); // → null كما تتوقع من المثال السابق، سيُعيد Object.getPrototypeOf سلسلة prototype للكائن. تنحدر الدوال من Function.prototype أما المصفوفات فتنحدر من Array.prototype، كما في المثال التالي: console.log(Object.getPrototypeOf(Math.max) == Function.prototype); // → true console.log(Object.getPrototypeOf([]) == Array.prototype); // → true سيكون لكائن النموذج الأولي المشابه لهذا، نموذج أولي خاص به وهو Object.prototype غالبًا، وذلك لاستمراره بتوفير توابع مثل toString؛ وتستطيع استخدام Object.create لإنشاء كائن مع نموذج أولي بعينه، كما في المثال التالي: let protoRabbit = { speak(line) { console.log(`The ${this.type} rabbit says '${line}'`); } }; let killerRabbit = Object.create(protoRabbit); killerRabbit.type = "killer"; killerRabbit.speak("SKREEEE!"); // → The killer rabbit says 'SKREEEE!' تُعَدّ خاصية مثل speak(line)‎ في تعبير الكائن طريقةً مختصرةً لتعريف تابع ما، إذ تنشِئ خاصيةً اسمها speak، وتعطيها دالةً على أساس قيمة لها؛ كما يتصرف الأرنب "proto" في المثال السابق على أساس حاوية للخصائص التي تشترك فيها جميع الأرانب؛ أما في حالة مثل الأرنب القاتل killer rabbit، فيحتوي على خصائص لا تنطبق إلا عليه -نوعه في هذه الحالة-، كما يأخذ خصائصًا مشتركةً من نموذجه الأولي. الأصناف Classes يحاكي نظام النماذج الأولية في جافاسكربت (أي سلسلة prototype كما أشرنا في الأعلى) مفهوم الأصناف Classes في البرمجة كائنية التوجه، حيث تحدِّد هذه الأصناف الشكل الذي سيكون عليه نوع ما من كائن، وذلك بتحديد توابعه وخصائصه، كما يُدعى مثل ذلك الكائن بنسخة instance من الصنف. تُعَدّ النماذج الأولية مفيدةً هنا في تحديد الخصائص المشتركة بين جميع نُسَخ الصنف التي لها القيمة نفسها مثل التوابع؛ أما الخصائص المختلفة بين كل نسخة -كما في حالة خاصية type لأرنبنا في المثال السابق-، فيجب تخزينها في الكائن نفسه مباشرةً. لذا عليك إنشاء كائنًا مشتقًا من النموذج الأولي المناسب من أجل إنشاء نسخة من صنف ما، لكن في الوقت نفسه يجب التأكد من امتلاكه الخصائص الواجب وجودها في نُسَخ ذلك الصنف، وهذا ما يمثل وظيفة دالة الباني constructor، انظر ما يلي: function makeRabbit(type) { let rabbit = Object.create(protoRabbit); rabbit.type = type; return rabbit; } توفر جافاسكربت طريقةً لتسهيل تعريف هذا النوع من الدوال، فإذا وضعتَ كلمة new المفتاحية أمام استدعاء الدالة مباشرةً، فستُعامَل الدالة على أساس باني، وهذا يعني أنه سيُنشَأ الكائن الذي يحمل النموذج الأولي المناسب تلقائيًا، بحيث يكون مقيدًا بـ this في الدالة، ثم يُعاد في نهاية الدالة، ويمكن العثور على كائن النموذج الأولي المستخدَم عند بناء الكائنات من خلال أخذ خاصية protoype لدالة الباني. function Rabbit(type) { this.type = type; } Rabbit.prototype.speak = function(line) { console.log(`The ${this.type} rabbit says '${line}'`); }; let weirdRabbit = new Rabbit("weird"); تحصل البواني، بل كل الدوال، على خاصية اسمها prototype تحمل بدورها كائنًا فارغًا مشتقًا من Object.prototype، وتستطيع استبدال كائن جديد به إن شئت أو إضافة خصائص إلى الكائن الجديد كما في المثال. تتكوّن أسماء البواني من الحروف الكبيرة لتمييزها عما سواها، ومن المهم إدراك الفرق بين الطريقة التي يرتبط بها النموذج الأولي بالباني من خلال خاصية prototype، والطريقة التي يكون للكائنات فيها نماذج أولية -والتي يمكن إيجادها باستخدام Object.getPrototypeOf. Function.Prototype هو النموذج الأولي الفعلي للباني بما أنّ البواني ما هي إلا دوال في الأصل، وتحمل خاصية prototype الخاصة به النموذج الأولي المستخدَم للنسخ التي أنشِئت من خلاله. console.log(Object.getPrototypeOf(Rabbit) == Function.prototype); // → true console.log(Object.getPrototypeOf(weirdRabbit) == Rabbit.prototype); // → true صياغة الصنف Class Notation ذكرنا أن أصناف جافاسكربت ما هي إلا دوال بانية مع خاصية النموذج الأولي، وقد كان ذلك حتى عام 2015؛ أما الآن فقد تحسنت الصيغة التي صارت عليها كثيرًا، انظر إلى ما يلي: class Rabbit { constructor(type) { this.type = type; } speak(line) { console.log(`The ${this.type} rabbit says '${line}'`); } } let killerRabbit = new Rabbit("killer"); let blackRabbit = new Rabbit("black"); تبدأ كلمة class المفتاحية تصريح صنفٍ يسمح لنا بتعريف باني ومجموعة توابع في مكان واحد، كما يمكن كتابة أيّ عدد من التوابع بين قوسي التصريح، لكن يُعامَل التابع الحامل لاسم constructor معاملةً خاصةً، إذ يوفِّر وظيفة الباني الفعلية التي ستكون مقيدة بالاسم Rabbit، في حين تُحزَّم التوابع الأخرى في النموذج الأولي لذلك الباني، ومن ثم يكون تصريح الصنف الذي ذكرناه قبل قليل مكافئًا لتعريف الباني من القسم السابق، كونه يبدو أفضل للقارئ. ولا تسمح تصريحات الأصناف حاليًا إلا بإضافة التوابع إلى النموذج الأولي، وهي الخصائص التي تحمل دوالًا، رغم أن ذلك قد يكون مرهقًا إذا أردت حفظ قيمة غير دالّية non-function هناك، وقد يتحسن ذلك في الإصدار القادم من اللغة، لكن حتى ذلك الحين تستطيع إنشاء مثل تلك الخصائص بتغيير النموذج الأولي مباشرةً بعد تعريف الصنف. يمكن استخدام class في التعليمات والتعابير على حد سواء، وشأنها في ذلك شأن function، حيث لا تعرِّف رابطةً عند استخدامها على أساس تعبير، وإنما تنتج الباني كقيمة فقط. وتستطيع إهمال اسم الصنف في تعبير الصنف، كما في المثال التالي: let object = new class { getWord() { return "hello"; } }; console.log(object.getWord()); // → hello إعادة تعريف الخصائص المشتقة تُضاف الخاصية إلى الكائن نفسه عند إضافتها إليه سواءً كان موجودًا في النموذج الأولي أم غير موجود، فإن كان ثمة خاصية موجودة بالاسم نفسه في النموذج الأولي، فلن تؤثِّر هذه الخاصية في الكائن بما أنها مخفية الآن خلف الخاصية التي يملكها الكائن. Rabbit.prototype.teeth = "small"; console.log(killerRabbit.teeth); // → small killerRabbit.teeth = "long, sharp, and bloody"; console.log(killerRabbit.teeth); // → long, sharp, and bloody console.log(blackRabbit.teeth); // → small console.log(Rabbit.prototype.teeth); // → small يبيّن المخطط التالي الموقف بعد تشغيل الشيفرة السابقة، إذ يقبع النموذجين الأوليَين لـ Rabbit، وObject خلف killerRabbit على أساس حاجز خلفي له، بينما يُبحث عن الخصائص التي ليست موجودة في الكائن. وتبدو فائدة إعادة تعريف الخصائص overriding properties الموجودة في النموذج الأولي في التعبير عن الخصائص الاستثنائية في نُسَخ الأصناف العامة للكائنات، كما في مثال أسنان الأرنب rabbit teeth السابق، مع السماح للكائنات غير الاستثنائية بأخذ قيمة قياسية من نموذجها الأولي. كما يمكن استخدام إعادة التعريف لإعطاء تابع toString للنماذج الأولية للدالة والمصفوفة القياسيتين، بحيث يختلف عن النموذج الأساسي للكائن. console.log(Array.prototype.toString == Object.prototype.toString); // → false console.log([1, 2].toString()); // → 1,2 يعطي استدعاء toString على مصفوفة نتيجةً محاكيةً لاستدعاء join(",")‎. عليها، إذ تضع فواصل إنجليزية بين القيم الموجودة في المصفوفة؛ أما الاستدعاء المباشر لـ Object.prototype.toString مع مصفوفة، فينتج سلسلةً نصيةً مختلفةً، حيث تضع كلمة object واسم النوع بين أقواس مربعة، وذلك لعدم معرفة تلك الدالة بشأن المصفوفات، كما في المثال التالي: console.log(Object.prototype.toString.call([1, 2])); // → [object Array] الخرائط Maps استخدمنا كلمة map في المقال السابق في عملية تحويل هيكل البيانات بتطبيق دالة على عناصره، رغم بعد معنى الكلمة نفسها، التحويل، الدال عن الفعل الذي تنفذه، وهنا أيضًا وفي البرمجة عمومًا، فتُستخدَم هذه الكلمة كذلك لغرض مختلف لكنه قريب مما رأينا، وكلمة map على أساس اسم هي أحد أنواع هياكل البيانات الذي يربط القيم (المفاتيح) بقيم أخرى، فإذا أردت ربط الأسماء بأعمار مقابلة لها، فتستطيع استخدام كائنات لذلك، كما في المثال التالي: let ages = { Ziad: 39, Hasan: 22, Sumaia: 62 }; console.log(`Sumaia is ${ages["Sumaia"]}`); // → Sumaia is 62 console.log("Is Jack's age known?", "Jack" in ages); // → Is Jack's age known? false console.log("Is toString's age known?", "toString" in ages); // → Is toString's age known? true أسماء خصائص الكائن هنا هي أسماء الناس المذكورة في المثال، وقيم الخصائص هي أعمارهم، لكننا بالتأكيد لم نذكر أيّ شخص اسمه toString في تلك الرابطة، لكن لأن الكائنات العادية مشتقة من Object.prototype فيبدو الأمر وكأن الخاصية موجودة هناك، لهذا فمن الخطر معاملة الكائنات العادية مثل معاملة خرائط -النوع Map- هنا. لدينا عدة طرق مختلفة لتجنب هذه المشكلة، فمن الممكن مثلًا إنشاء كائنات بدون نموذج أولي، حتى إذا مرّرت null إلى Object.create، فلن يكون الكائن الناتج مشتقًا من Object.prototype، وعليه يمكن استخدامه بأمان على أساس خارطة. console.log("toString" in Object.create(null)); // → false يجب أن تكون أسماء خصائص الكائنات سلاسل نصية، فإن أردت ربطًا لا يمكن تحويل مفاتيحه بسهولة إلى سلاسل نصية -مثل الكائنات- فلا تستخدم كائنًا على أساس خارطة، ولحسن الحظ فتملك جافاسكربت صنفًا اسمه Map مكتوب لهذا الغرض خاصة، حيث يخزِّن حالة الربط ويسمح بأي نوع من المفاتيح. let ages = new Map(); ages.set("Ziad", 39); ages.set("Hasan", 22); ages.set("Sumaia", 62); console.log(`Sumaia is ${ages.get("Sumaia")}`); // → Sumaia is 62 console.log("Is Jack's age known?", ages.has("Jack")); // → Is Jack's age known? false console.log(ages.has("toString")); // → false تُعَدّ التوابع set، وget، وhas جزءًا من واجهة كائن Map، فليس من السهل كتابة هيكل بيانات لتحديث مجموعة كبيرة من القيم والبحث فيها، ولكن لا تقلق، فقد كفانا شخص آخر مؤنة ذلك، حيث نستطيع استخدام ما كتبه من خلال تلك الواجهة البسيطة. إذا أردت معاملة كائن عادي لديك على أساس خارطة (النوع Map) لسبب ما، فمن المهم معرفة أن Object.keys يعيد المفاتيح الخاصة بالكائن فقط، وليس تلك الموجودة في النموذج الأولي، كما تستطيع استخدام التابع hasOwnProperty على أساس بديل لعامِل in، حيث يتجاهل النموذج الأولي للكائن، كما في المثال التالي: console.log({x: 1}.hasOwnProperty("x")); // → true console.log({x: 1}.hasOwnProperty("toString")); // → false تعددية الأشكال Polymorphism إذا استدعيتَ دالة String -التي تحوِّل القيمة إلى سلسلة نصية- على كائن ما، فستستدعي التابع toString على ذلك الكائن لمحاولة إنشاء سلسلة نصية مفيدة منه. كما ذكرنا سابقًا، تعرِّف بعض النماذج الأولية القياسية (سلاسل prototype) إصدارًا من toString خاصًا بها، وذلك لتستطيع إنشاء سلسلة نصية تحتوي بيانات مفيدة أكثر من "[object Object]"، كما تستطيع فعل ذلك بنفسك إن شئت. Rabbit.prototype.toString = function() { return `a ${this.type} rabbit`; }; console.log(String(blackRabbit)); // → a black rabbit وهذه صورة بسيطة من مفهوم بالغ القوة والأثر، فإن كُتب جزء من شيفرة ما ليعمل مع كائنات بها واجهة معينة -تابع toString في هذه الحالة-، فيمكن إلحاق أي نوع من الكائنات الداعمة لتلك الواجهة بالشيفرة، حيث ستعمل دون مشاكل؛ وتسمى تلك التقنية بتعددية الأشكال، وتعمل الشيفرة المتعددة الأشكال مع قيم ذات أشكال مختلفة طالما أنها تدعم الواجهة التي تتوقعها. كما ذكرنا في المقال الرابع، تستطيع حلقة for/of التكرار على عدة أنواع من هياكل البيانات، وتلك حالة أخرى من تعددية الأشكال، حيث تتوقع مثل تلك الحلقات التكرارية من هيكل البيانات أن يكشف واجهة معينة، وهو ما تفعله المصفوفات والسلاسل النصية؛ كما نستطيع إضافة تلك الواجهة إلى كائناتنا الخاصة، لكننا نحتاج إلى معرفة ما هي الرموز symbols قبل فعل ذلك. الرموز Symbols تستطيع عدة واجهات استخدام اسم الخاصية نفسها لأشياء عدة، فمثلًا، نستطيع تعريف واجهة بحيث يحوِّل فيها التابع toString الكائن إلى قطعة من خيوط الغزل، لكن من غير الممكن لكائن أن يتوافق مع تلك الواجهة ومع الاستخدام القياسي لـ toString. هذه المشكلة سيئة لكنها لا تشغل بال من يكتب بجافاسكربت لأنها غير شائعة، ورغم هذا فقد وفر مصممو جافاسكربت لنا حلًا لهذه المشكلة، إذ أن تلك من وظيفتهم على أي حال. حين زعمنا أن أسماء الخصائص هي سلاسل نصية لم نكن محقين 100%، فرغم أنها حقًا سلاسل نصية إلا قد تكون رموزًا أيضًا، وهي -أي الرموز- قيم أنشِئت بواسطة دالة Symbol، كما تُعَدّ الرموز المنشَئة حديثًا فريدةً، على عكس السلاسل النصية، بحيث لا تستطيع إنشاء الرمز نفسه مرتين. let sym = Symbol("name"); console.log(sym == Symbol("name")); // → false Rabbit.prototype[sym] = 55; console.log(blackRabbit[sym]); // → 55 تُضمَّن السلسلة النصية الممررة إلى Symbol تلقائيًا حين تحوّلها إلى سلسلة نصية، كما تسهِّل التعرف على الرمز عند عرضه في الطرفية console مثلًا؛ ولأن الرموز فريدة ويمكن استخدامها على أساس أسماء للخصائص، فهي مناسبة لتعريف الواجهات التي يمكن وجودها مع الخصائص الأخرى مهما كانت أسماؤها. const toStringSymbol = Symbol("toString"); Array.prototype[toStringSymbol] = function() { return `${this.length} cm of blue yarn`; }; console.log([1, 2].toString()); // → 1,2 console.log([1, 2][toStringSymbol]()); // → 2 cm of blue yarn ومن الممكن إضافة خصائص رمز ما في الأصناف وتعبيرات الكائنات باستخدام أقواس مربعة حول اسم الخاصية، وبسبب ذلك سيُقيَّم اسم الخاصية مثل صيغة الوصول إلى الخاصية التي تستخدِم قوسين مربعين، حيث سيسمح لنا هذا بالإشارة إلى الرابطة التي تحمل الرمز. let stringObject = { [toStringSymbol]() { return "a jute rope"; } }; console.log(stringObject[toStringSymbol]()); // → a jute rope واجهة المكرر يُتوقع من الكائن المعطى لحلقة for/of قابليته للتكرار، ويعني ذلك أنّ به تابعًا مسمى مع الرمز Symbol.iterator، وهو قيمة رمز معرَّفة من قِبَل اللغة، ومخزَّنة على أساس خاصية لدالة Symbol، كما يجب على ذلك التابع إعادة كائن يوفر واجهةً ثانية تكون هي المكرِّر iterator الذي يقوم بعملية التكرار، ولديه تابع next الذي يعيد النتيجة التالية التي يجب أن تكون بدورها كائنًا مع خاصية value التي توفر القيمة التالية إن كانت موجودة، وخاصية done التي تعيد true إن لم تكن ثمة نتائج أخرى، وتعيد false إن كان ثَمَّ نتائج بعد. لاحظ أن أسماء الخصائص: next، وvalue، وdone، هي سلاسل نصية عادية وليست رموزًا؛ أما الرمز الوحيد هنا فهو Symbol.iterator، والذي سيضاف غالبًا إلى كائنات كثيرة، كما نستطيع استخدام تلك الواجهة بأنفسنا كما يلي: let okIterator = "OK"[Symbol.iterator](); console.log(okIterator.next()); // → {value: "O", done: false} console.log(okIterator.next()); // → {value: "K", done: false} console.log(okIterator.next()); // → {value: undefined, done: true} دعنا نطبق هنا هيكل بيانات قابلًا للتكرار، حيث سنبني صنفَ matrix يتصرف على أساس مصفوفة ثنائية الأبعاد. class Matrix { constructor(width, height, element = (x, y) => undefined) { this.width = width; this.height = height; this.content = []; for (let y = 0; y < height; y++) { for (let x = 0; x < width; x++) { this.content[y * width + x] = element(x, y); } } } get(x, y) { return this.content[y * this.width + x]; } set(x, y, value) { this.content[y * this.width + x] = value; } } يخزِّن الصنف محتوياته في مصفوفة واحدة من عنصرين فقط، هما: العرض، والطول width*height، وتُخزَّن العناصر صفًا صفًا، فيُخزن العنصر الثالث في الصف الخامس مثلًا -باستخدام الفهرسة الصفرية التي تبدأ من الصفر- في الموضع ‎4 * width + 2‎. تأخذ دالة الباني العرض، والطول، ودالة element اختيارية ستُستخدم لكتابة القيم الابتدائية؛ أما لجلب العناصر وتحديثها في المصفوفة الثنائية، فلدينا التابعان get، وset. حين نكرر على مصفوفة ما، فنحن بحاجة إلى معرفة موضع العناصر إضافة إلى العناصر نفسها، لذا سنجعل المكرِّر ينتج كائنات لها خصائص x، وy، وvalue. class MatrixIterator { constructor(matrix) { this.x = 0; this.y = 0; this.matrix = matrix; } next() { if (this.y == this.matrix.height) return {done: true}; let value = {x: this.x, y: this.y, value: this.matrix.get(this.x, this.y)}; this.x++; if (this.x == this.matrix.width) { this.x = 0; this.y++; } return {value, done: false}; } } يتتبع الصنف سير التكرار على المصفوفة الثنائية في الخصائص x، وy، ويبدأ التابع next بالتحقق من الوصول لأسفل المصفوفة الثنائية، فإن لم يصل إليه، فسينشِئ الكائن الذي يحمل القيمة الحالية أولًا، ثم يحدِّث موضعه، وبعد ذلك ينقله إلى السطر التالي إن تطلب الأمر. دعنا نهيئ صنف Matrix ليكون قابلًا للتكرار، وانتبه إلى استخدامنا المعالجة اللاحقة للنموذج الأولي بين الحين والآخر في هذه السلسلة لإضافة توابع إلى الأصناف، وذلك لتبقى الأجزاء المفردة من الشيفرة صغيرةً ومستقِلة؛ أما في البرامج العادية التي لا تحتاج فيها إلى تقسيم الشيفرة إلى أجزاء صغيرة، فستصرِّح عن هذه التوابع مباشرةً في الصنف. Matrix.prototype[Symbol.iterator] = function() { return new MatrixIterator(this); }; نستطيع الآن تطبيق التكرار على مصفوفة ما باستخدام for/of. let matrix = new Matrix(2, 2, (x, y) => `value ${x},${y}`); for (let {x, y, value} of matrix) { console.log(x, y, value); } // → 0 0 value 0,0 // → 1 0 value 1,0 // → 0 1 value 0,1 // → 1 1 value 1,1 التوابع الجالبة والضابطة والساكنة تتكون الواجهات من التوابع غالبًا، وقد تتضمن خصائص بها قيم غير دالية، فمثلًا، تملك كائنات Map خاصية size، والتي تخبرك كم عدد المفاتيح المخزَّنة فيها. ليس من الضروري لمثل هذا الكائن أن يحسب ويخزن خاصية مشابهة لتلك مباشرةً في النسخة instance التي لديه، بل حتى الخصائص التي يمكن الوصول إليها مباشرةً قد تخفي استدعاءً إلى تابع، حيث تسمى مثل تلك التوابع بالتوابع الجالبة getters، وتُعرَّف بكتابة get أمام اسم التابع في تعبير الكائن أو تصريح الصنف. let varyingSize = { get size() { return Math.floor(Math.random() * 100); } }; console.log(varyingSize.size); // → 73 console.log(varyingSize.size); // → 49 يُستدعى التابع المرتبط بخاصية size للكائن كلما قرأ أحد من منها، وتستطيع تنفيذ شيء مشابه حين يكتب أحدهم في خاصية ما باستخدام تابع ضابط setter. class Temperature { constructor(celsius) { this.celsius = celsius; } get fahrenheit() { return this.celsius * 1.8 + 32; } set fahrenheit(value) { this.celsius = (value - 32) / 1.8; } static fromFahrenheit(value) { return new Temperature((value - 32) / 1.8); } } let temp = new Temperature(22); console.log(temp.fahrenheit); // → 71.6 temp.fahrenheit = 86; console.log(temp.celsius); // → 30 يسمح لك صنف Temperature في المثال أعلاه بقراءة درجة الحرارة وكتابتها سواءً بمقياس السليزيوس أو الفهرنهايت، لكنها تخزِّن داخلها درجات السليزيوس فقط، وتحوِّل من وإلى سليزيوس في التابع الجالب والضابط لـ fahrenheit تلقائيًا. قد تحتاج أحيانًا إلى إلحاق بعض الخصائص لدالة الباني الخاصة بك مباشرةً بدلًا من النموذج الأولي، ولا تملك مثل تلك التوابع وصولًا إلى نسخة صنف، لكن يمكن استخدامها لتوفير طرق بديلة وإضافية لإنشاء النسخ. تُخزَّن التوابع المكتوبة قبل اسمها static على الباني، وذلك داخل التصريح عن الصنف، وعليه فيسمح لك صنف Temperature بكتابة Temperature.fromFahrenheit(100)‎ لإنشاء درجة حرارة باستخدام مقياس فهرنهايت. الوراثة Inheritance تتميز بعض المصفوفات بأنها تماثلية symmetric، بحيث إذا عكست إحداها حول قطرها الذي يبدأ من أعلى اليسار، فستبقى كما هي ولا تتغير، أي ستبقى القيمة المخزنة في الموضع (x،y) كما هي في الموضع (y،x). تخيل أننا نحتاج إلى هيكل بيانات مثل Matrix، لكن يجب ضمان تماثلية المصفوفة وبقائها كذلك، وهنا نستطيع كتابة هذا من الصفر، لكننا سنكرر شيفرةً مشابهةً كثيرًا لما كتبناه سابقًا. يسمح نظام النموذج الأولي في جافاسكربت بإنشاء صنف جديد محاكي لصنف قديم لكن مع تعريفات جديدة لبعض خصائصه، ويكون النموذج الأولي للصنف الجديد مشتقًا من القديم لكن مع إضافة تعريف جديد إلى التابع set مثلًا، ويسمى ذلك بالاكتساب أو الوراثة inheritance، إذ يرث الصنف الجديد خصائصه وسلوكه من الصنف القديم. class SymmetricMatrix extends Matrix { constructor(size, element = (x, y) => undefined) { super(size, size, (x, y) => { if (x < y) return element(y, x); else return element(x, y); }); } set(x, y, value) { super.set(x, y, value); if (x != y) { super.set(y, x, value); } } } let matrix = new SymmetricMatrix(5, (x, y) => `${x},${y}`); console.log(matrix.get(2, 3)); // → 3,2 يشير استخدام كلمة extends إلى وجوب عدم اعتماد هذا الصنف على النموذج الأولي الافتراضي Object مباشرةً، وإنما على صنف آخر يسمى بالصنف الأب superclass؛ أما الصنف المشتق فيكون اسمه الصنف الفرعي، أو الابن subclass. يستدعي الباني لتهيئة نسخة من SymmetricMatrix باني صنف الأب من خلال كلمة super المفتاحية، وهذا ضروري لأنّ الكائن الجديد سيحتاج إلى خصائص النسخة التي تملكها المصفوفات، إذا تصرَّف مثل Matrix. كما يغلِّف الباني دالة element لتبديل إحداثيات القيم أسفل خط القطر، وذلك لضمان تماثل المصفوفة. يُستخدَم super مرةً أخرى من التابع set، وذلك لاستدعاء تابع معين من مجموعة توابع الصنف الأب؛ كما سنعيد تعريف set لكن لن نستخدم السلوك الأصلي، حيث لن ينجح استدعاؤه بسبب إشارة this.set إلى set الجديد، كذلك يوفر super الواقع داخل توابع الصنف، طريقةً لاستدعاء التوابع كما عُرِّفت في الصنف الأب. وتسمح لنا الوراثة ببناء أنواع بيانات مختلفة من أنواع موجودة مسبقًا بقليل من الجهد، وهذه -أي الوراثة- جزء أساسي في ثقافة البرمجة كائنية التوجه جنبًا إلى جنب مع التغليف وتعددية الأشكال، لكن لأن هذين الآخرَين يُعتد بهما كثيرًا في البرمجة على أساس أساليب مهمة ومفيدة، فإنّ الوراثة قد صارت محل نظر، ففي حين يُستخدَم كل من التغليف وتعددية الأشكال في فصل أجزاء الشيفرات عن بعضها مما يقلل من تعقيد البرنامج عمومًا، فالوراثة على العكس من ذلك، إذ تربط الأصناف معًا منشِئًة مزيدًا من التعقيد، لأن عليك في الغالب معرفة كيفية عمل ذلك الصنف حين تحتاج إلى الوراثة منه، بخلاف إن لم تفعل شيئًا سوى استخدامه. وإننا نستخدمه بين الحين والآخر في برامجنا، لكن لا يحملنك ذلك على التفكير فيه أول شيء، فليس من الحكمة جعل بناء هرميات من الأصناف (شجرة عائلة من الأصناف) خيارك الأول في حل المشاكل. عامل instanceof توفر جافاسكربت عاملًا ثنائيًا يسمى instanceof، حيث نستخدمه إذا أردنا معرفة إن كان الكائن مشتقًا من صنف بعينه. console.log( new SymmetricMatrix(2) instanceof SymmetricMatrix); // → true console.log(new SymmetricMatrix(2) instanceof Matrix); // → true console.log(new Matrix(2, 2) instanceof SymmetricMatrix); // → false console.log([1] instanceof Array); // → true سينظر العامل في الأنواع المكتسبة، وسيجد أن symmetricMatrix نسخةٌ من Matrix، كما يمكن استخدام العامل مع البواني القياسية مثل Array، فكل كائن تقريبًا ما هو إلا نسخة من Object. خاتمة لقد رأينا أنّ نطاق تأثيرالكائنات يتعدى حمل خصائصها، إذ لها نماذج أولية -والتي بدورها كائنات أيضًا-، وتتصرف كما لو كان لديها خصائص ليست لديها على الحقيقة طالما أن النموذج الأولي به تلك الخصائص، كما تمكّنا من معرفة الكائنات البسيطة لها Object.prototype على أساس نموذج أولي لها. يمكن استخدام البواني -وهي دوال تبدأ أسماؤها بحرف إنجليزي كبير- مع عامل new لإنشاء كائنات جديدة، وسيكون النموذج الأولي للكائن هو الكائن الموجود في خاصية prototype للباني، ونستطيع الاستفادة من ذلك بوضع جميع الخصائص التي تتشاركها القيم المعطاة -من النوع نفسه- في نماذجها الأولية. كذلك عرفنا صيغة class التي توفر طريقةً واضحةً لتعريف الباني ونموذجه الأولي. تستطيع تعريف الجالبات والضابطات لاستدعاء التوابع سرًا في كل مرة يصل فيها إلى خاصية كائن ما، وقد عرفنا أن التوابع الساكنة ما هي إلا توابع مخزَّنة في باني الصنف بدلًا من نموذجه الأولي، ثم شرحنا كيف أن عامل instanceof يستطيع إخبارك إن أعطيته كائنًا وبانيًا، وما إذا كان الكائن نسخةً من الباني أم لا. واعلم أنك تستطيع باستخدام الكائنات تحديد واجهة لها، وتخبر جميع أجزاء الشيفرة بأن عليهم التحدث إلى كائنك من خلال تلك الواجهة فقط، كما تُغلَّف بقية التفاصيل التي يتكون منها الكائن وتختفي خلف الواجهة. ويمكن لأكثر من نوع استخدام تلك الواجهة، فتعرف الشيفرة التي كُتبت لتستخدِم واجهةً ما كيف تعمل مع أي عدد من الكائنات المختلفة التي توفر الواجهة تلقائيًا ، وهذا ما يسمى بتعددية الأشكال. حين تستخدم عدة أصناف لا تختلف فيما بينها إلا في بعض التفاصيل، فيمكن كتابة أصناف جديدة منها على أساس أصناف فرعية، ترث جزءًا من سلوكها. تدريبات النوع المتجهي اكتب الصنف Vec الذي يمثل متجهًا في فضاء ثنائي الأبعاد، حيث يأخذ المعامِلين x، وy -وهما أرقام-، ويحفظهما في خصائص بالاسم نفسه. أعطِ النموذج الأولي للصنف Vec تابعَين، هما: plus، وminus، اللذان يأخذان متجهًا آخر على أساس معامِل، ويُعيدان متجهًا جديدًا له مجموع قيم x، وy للمتجهين (this، والمعامِل)؛ أو الفرق بينهما. أضف الخاصية الجالبة length إلى النموذج الأولي الذي يحسب طول المتجه، وهو المسافة بين النقطة (x,y) والإحداثيات الصفرية (0,0). تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. // ضع شيفرتك هنا. console.log(new Vec(1, 2).plus(new Vec(2, 3))); // → Vec{x: 3, y: 5} console.log(new Vec(1, 2).minus(new Vec(2, 3))); // → Vec{x: -1, y: -1} console.log(new Vec(3, 4).length); // → 5 إرشادات للحل إذا لم تكن تعرف كيف تبدو تصريحات class، فانظر إلى مثال صنف Rabbit. يمكن إضافة خاصية جالبة إلى الباني من خلال وضع كلمة get قبل اسم التابع، ولحساب المسافة من (0,0) إلى (x,y)، فيمكن استخدام نظرية فيثاغورث التي تقول: أن مربع المسافة التي نريدها يساوي مجموع مربعي x و y، وعلى ذلك يكون ‎√(x2 + y2)‎ هو العدد الذي نريده، ويُحسَب الجذر التربيعي في جافاسكربت باستخدام Math.sqrt. المجموعات توفر بيئة جافاسكربت القياسية هيكل بيانات اسمه Set، إذ يحمل مجموعةً من القيم مثل نسخة من Map، لكن على عكس Map فهو لا يربط قيمًا أخرى بها، بل يتتبع القيم ليعرف أيها تكون جزءًا من المجموعة. ولا يمكن للقيمة الواحدة أن تكون جزءًا من مجموعة ما أكثر من مرة واحدة، ولا يحدث أي تأثير حين تضاف مرةً أخرى. اكتب صنفًا اسمه Group -بما أنّ Set مأخوذ من قبل-، واجعل له التوابع الآتية: add، وdelete، وhas، ليكون مثل Set، بحيثما ينشئ بانيه مجموعةً فارغةً، ويضيف add قيمةً إلى المجموعة فقط إن لم تكن عضوًا بالفعل في المجموعة، كما يحذف delete وسيطه من المجموعة إن كان عضوًا فيها، ويعيد has قيمةً بوليانيةً توضح هل وسيطه عضو في المجموعة أم لا. استخدم عامِل ===، أو شيئًا يحاكيه مثل indexof، لمعرفة ما إذا كانت قيمتان متطابقين، وأعط الصنف التابع الساكن from الذي يأخذ كائنًا قابلًا للتكرار على أساس وسيط، كما ينشئ مجموعةً تحتوي على جميع القيم المنتَجة من خلال التكرار عليها. تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. class Group { // ضع شيفرتك هنا. } let group = Group.from([10, 20]); console.log(group.has(10)); // → true console.log(group.has(30)); // → false group.add(10); group.delete(10); console.log(group.has(10)); // → false إرشادات للحل تكون الطريقة الأسهل لحل هذا التدريب بتخزين مصفوفة من أعضاء المجموعة في خاصية لإحدى النُسَخ، ويمكن استخدام التابع includes، أو indexOf للتحقق من وجود قيمة ما في المصفوفة. ويمكن لباني الصنف الخاص بك إسناد تجميعة الأعضاء إلى مصفوفة فارغة، وعند استدعاء add فيجب التحقق هل القيمة المعطاة موجودة في المصفوفة أم يضيفها باستخدام push مثلًا. قد يكون حذف عنصر من مصفوفة في delete مبهمًا قليلًا، لكن تستطيع استخدام filter لإنشاء مصفوفة جديدة بدون القيمة، ولا تنس كتابة النسخة الجديدة من المصفوفة لتحل محل الخاصية التي تحمل الأعضاء. يمكن للتابع from استخدام حلقة for/of التكرارية للحصول على القيم من الكائن القابل للتكرار، ويستدعي add لوضعها في مجموعة منشأة حديثًا. المجموعات القابلة للتكرار أنشئ الصنف Group من التدريب السابق، واستعن بالقسم الخاص بواجهة المكرر من هذا المقال إن احتجت إلى رؤية الصيغة الدقيقة للواجهة. إذا استخدمت مصفوفةً لتمثيل أعضاء المجموعة، فلا تُعِد المكرِّر المنشَأ باستدعاء التابع Symbol.iterator على المصفوفة، فهذا وإن كان سيعمل بدون مشاكل، إلا أنه سينافي الهدف من التدريب. لا بأس إن تصرَّف المكرر الخاص بك تصرفًا غير مألوف عند تعديل المجموعة أثناء التكرار. تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. // ضع شيفرتك هنا، والشيفرة التي من .المثال السابق for (let value of Group.from(["a", "b", "c"])) { console.log(value); } // → a // → b // → c إرشادات للحل ربما من الأفضل تعريف صنف GroupIterator جديد، كما يجب أن يكون لنُسَخ المكرر خاصية تتبع الموضع الحالي في المجموعة، بحيث تتحقق في كل مرة يُستدعى فيها next مما إذا كانت قد انتهت أم لا، فإن لم تنته فستتحرك متجاوزةً القيمة الحالية وتعيدها. يحصل الصنف Group على تابع يسمى من قِبل Symbol.iterator`، ويعيد عند استدعائه نسخةً جديدةً من صنف المكرر لتلك المجموعة. استعارة تابع ذكرنا أعلاه هنا أن hasOwnProperty لكائن يمكن استخدامه على أساس بديل قوي لعامِل in إذا أردت تجاهل خصائص النموذج الأولي، لكن ماذا لو كانت خارطتك map تحتاج إلى كلمة hasOwnProperty؟ لن تستطيع حينها استدعاء هذا التابع بما أن خاصية الكائن تخفي قيمة التابع. هل تستطيع التفكير في طريقة لاستدعاء hasOwnProperty على كائن له خاصية بهذا الاسم؟ تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. let map = {one: true, two: true, hasOwnProperty: true}; // أصلح هذا الاستدعاء console.log(map.hasOwnProperty("one")); // → true إرشادات للحل تذكّر أن التوابع الموجودة في الكائنات المجردة تأتي من Object.prototype، كما تستطيع استدعاء دالة مع رابطة this خاصة من خلال استخدام التابع call. ترجمة -بتصرف- للفصل السادس من كتاب Elequent Javascript لصاحبه Marijn Haverbeke. اقرأ أيضًا المقال السابق: الدوال في جافاسكريبت. هياكل البيانات: الكائنات والمصفوفات في جافاسكريبت.

يختلف هذا المقال قليلًا عن باقي الفصول، إذ سأدَع الحديث عن النظريات قليلًا لننشئ نحن وأنت برنامجًا سويًا، فالنظرية وإن كانت مهمة جدًا لتعلم كيفية البرمجة، إلا أنّ قراءة البرامج الحقيقية وفهم شيفراتها لا تقل أهمية، ومشروعنا في هذا المقال هو بناء روبوت ينفِذ مهمة في عالم افتراضي، وستكون تلك المهمة توصيل الطرود واستلامها. قرية المرج Meadowfield سيعمل الروبوت الخاص بنا في قرية صغيرة تُدعى قرية المرج، حيث يوجد فيها أحد عشر مكانًا بينها أربعة عشر طريقًا، ويمكن وصف القرية بالمصفوفة التالية: const roads = [ "Salma's House-Omar's House", "Salma's House-Cabin", "Salma's House-Post Office", "Omar's House-Town Hall", "Sara's House-Mostafa's House", "Sara's House-Town Hall", "Mostafa's House-Sama's House", "Sama's House-Farm", "Sama's House-Shop", "Marketplace-Farm", "Marketplace-Post Office", "Marketplace-Shop", "Marketplace-Town Hall", "Shop-Town Hall" ]; وتكوِّن شبكة الطرق في القرية مخططًا graph، وهو عبارة عن تجميعة من نقاط لتمثل الأماكن في القرية، مع خطوط تصل بينها بحيث تمثل الطرق، وسيكون هذا هو العالم الذي سيتحرك الروبوت فيه. لكن ليس من السهل التعامل مع مصفوفة السلاسل النصية السابقة، إذ لا نريد إلا الوجهات التي يمكننا الذهاب إليها من أي نقطة معطاة لنا، وعلى ذلك فسنحوِّل قائمة الطرق إلى هيكل بيانات يخبرنا بالمناطق التي نستطيع الذهاب إليها من كل نقطة أو مكان، انظركما يلي: function buildGraph(edges) { let graph = Object.create(null); function addEdge(from, to) { if (graph[from] == null) { graph[from] = [to]; } else { graph[from].push(to); } } for (let [from, to] of edges.map(r => r.split("-"))) { addEdge(from, to); addEdge(to, from); } return graph; } const roadGraph = buildGraph(roads); تُنشئ دالة buildGraph كائن خارطة map object عند إعطائها مصفوفة من الحدود edges، حيث تخزن فيها لكل عقدةٍ مصفوفةً من العقد المتصلة بها. كما تستخدِم تابع method للذهاب من سلسلة الطريق النصية التي تحمل الصيغة "Start-End" إلى مصفوفات من عنصرين تحتوي على البداية والنهاية على أساس سلسلتَين منفصلتين. المهمة سيتحرك الروبوت داخل القرية، إذ لديه طرود في أماكن مختلفة فيها، حيث يحمل كل طرد عنوانًا يجب نقله إليه؛ وسيلتقط الروبوت الطرودَ حين وصوله إليها، ثم يتركها عند وصوله إلى الوجهة المرسَل إليها، ويجب أن يقرر في كل نقطة وجهته التالية، ولا تنتهي مهمته إلا عند توصيل جميع الطرود. لكن أولًا يجب تعريف عالم افتراضي يصف هذه العملية، وذلك لنتمكّن من محاكاته، ويكون هذا النموذج قادر على إخبارنا بموقع الروبوت والطرود معًا، كما يجب تحديث هذا النموذج عندما يقرر الروبوت الذهاب إلى مكان جديد. إن كنت تفكر بأسلوب البرمجة كائنية التوجه، سيكون دافعك الأول هو البدء بتعريف كائنات للعناصر المختلفة في هذا العالم الذي أنشأناه، فصنف للروبوت، وآخر للطرد، وصنف ثالث للأماكن ربما، ثم تحمِل هذه الأصناف بعد ذلك خصائصًا تصف حالتها، كما في حالة كومة الطرود عند موقع ما، والتي يمكننا تغييرها عند إجراء تحديث لهذا العالم. لكن هذا خطأ في أغلب الحالات على الأقل، فكون شيء ما يحاكي الكائن لا يعني وجوب معاملته على أساس كائن في برنامجك؛ كما أنّ كتابة الأصناف في برنامجك دون داعي حقيقي لها، ستُنشئ تجميعةً من الكائنات المرتبطة ببعضها بعضًا لكل منها حالة داخلية متغيرة، وتكون مثل تلك البرامج صعبة الفهم وسهلة التعطل. لدينا أسلوبًا أفضل من ذلك، وهو ضغط حالة القرية إلى أقل فئة ممكنة من القيم التي تعرِّفها، فيكون لدينا الموقع الحالي للروبوت، وتجميعة الطرود غير المسلَّمة، والتي يحمل كل منها موقعه الحالي وعنوان التسليم، وحسبنا هذا! بينما نحن في ذلك، فعلينا التأكد أنه حين يتحرك الروبوت من موقعه، فعلينا حساب حالة جديدة وفق الموقف الذي يكون بعد التحرك، وذلك دون تغيير الحالة الأولى، انظر كما يلي: class VillageState { constructor(place, parcels) { this.place = place; this.parcels = parcels; } move(destination) { if (!roadGraph[this.place].includes(destination)) { return this; } else { let parcels = this.parcels.map(p => { if (p.place != this.place) return p; return {place: destination, address: p.address}; }).filter(p => p.place != p.address); return new VillageState(destination, parcels); } } } يتحقق التابع move أولًا إن كان ثمة طريق من الموقع الحالي إلى موقع الوِجهة، وإن لم يكن، فسيعيد الحالة القديمة بما أنّ هذه الخطوة غير صالحة، ثم يُنشئ حالةً جديدةً يكون فيها موقع الوِجهة هو الموقع الجديد للروبوت. لكن سيحمل هذا الروبوت معه طرودًا أخرى غير هذا الطرد، ويأخذها معه إلى موقع تسليم الطرد المسمى، ثم يتابع حملها معه بعد تسليم الطرد، ليذهب بكل منها إلى موقع تسليمه الذي يخصه، ولكي نحصل على بيانات تلك الطرود عند أي نقطة زمنية نريدها، فسنحتاج إلى إنشاء فئة set جديدة نضع فيها تلك الطرود التي يحملها إلى الموقع الجديد، ثم يترك الطرود الواجب تسليمها في موقع التسليم، أي نحذفها من فئة الطرود غير المسلَّمة. ويتكفل بعملية الانتقال استدعاء map، بينما نستدعي filter ليتولى عملية التسليم. لا تتغير كائنات الطرود عند نقلها، وإنما يعاد إنشاؤها، ويعطينا التابع move حالة جديدة للقرية مع ترك الحالة القديمة كما هي دون تغيير، انظر كما يلي: let first = new VillageState( "Post Office", [{place: "Post Office", address: "Salma's House"}] ); let next = first.move("Salma's House"); console.log(next.place); // → Salma's House console.log(next.parcels); // → [] console.log(first.place); // → Post Office تُسلَّم الطرود عند مواضع تسليمها مع حركة الروبوت بين تلك المواقع، ويُرى أثر ذلك في الحالة التالية، لكن ستظل الحالة الابتدائية تصف الموقف الذي يكون فيه الروبوت عند مكتب البريد ومعه الطرد الغير مسلَّم بعد. البيانات الثابتة Persistent Data تُسمى هياكل البيانات التي لا تتغير بالهياكل الثابتة persistent، أو غير القابلة للتغير immutable، وتحاكي السلاسل النصية والأرقام في بقائها كما هي، بدلًا من احتواء أشياء مختلفة في كل مرة. بما أن كل شيء في جافاسكربت قابل للتغير تقريبًا، فسيتطلب العمل مع كائنات أو بيانات ثابتة جهدًا، وعملًا إضافيًا، ونوعًا من التقييد، حيث لدينا دالة Object.freeze من أجل هذا، إذ تؤثر على الكائن وتجمده، وذلك لتجعله يتجاهل الكتابة على خصائصه، فتستطيع استخدام ذلك لضمان ثبات كائناتك إن أردت، لكن تذكر أن هذا التجميد يعني أن الحاسوب سيبذل مزيدًا من الجهد. نفضل إخبار العامة بترك الكائن الفلاني وشأنه وعدم العبث به، آملين تذكّرهم ذلك، بدلًا من إخبارهم بتجاهل تحديثات بعينها. let object = Object.freeze({value: 5}); object.value = 10; console.log(object.value); // → 5 لكن هنا يبرز سؤال إن كنت منتبهًا، فإن كانت اللغة نفسها تحثنا على جعل كل شيء متغيرًا وتتوقع منا ذلك، فلماذا نخرج عن هذا المسلك لنجعل بعض الكائنات ثابتةً لا تقبل التغيير؟ الإجابة بسيطة وهي أن هذا سيساعدنا في فهم برامجنا أكثر، إذ يتعلق الأمر بإدارة التعقيد لبرامجنا، فإن كانت الكائنات التي في نظامنا ثابتةً ومستقرةً، فيمكننا إجراء عمليات عليها إجراءً معزولًا -حيث سيعطينا التحرك إلى منزل سلمى مثلًا من أي حالة بدء معطاة الحالة الجديدة نفسها في كل مرة-،؛ أما إن كانت الكائنات تتغير مع الوقت، فسيضيف هذا بعدًا جديدًا من التعقيد إلى العمليات والتفكير المنطقي لحل المشكلة. وربما تقول أن مسألة توصيل الطرود، والروبوت، وهذه القرية الصغيرة، سهل أمرها ويمكن إدارتها، وربما أنت محق، لكن المعيار الذي يحدد نوع النظم الممكن بناؤها هو فهمنا نحن لتلك الأنظمة ومدى ما يمكننا فهمه مطلقًا، فأيّ شيء يسرّع فهم شيفرتك، فسيمهد لك الطريق لبناء نظم أكثر تطورًا. لكن رغم سهولة فهم النظم المبنية على هياكل بيانات ثابتة، فقد يكون من الصعب تصميم نظام مثل هذا، وخاصةً إن لم تكن لغة البرمجة التي تستخدمها مصمَّمةً لذلك، كما سنبحث عن فرص استخدام هياكل البيانات الثابتة في هذه السلسلة مع استخدامنا للهياكل المتغيرة كذلك. المحاكاة ينظر روبوت التوصيل إلى العالم، ويقرر الاتجاه الذي يريد السير فيه، وعليه فيمكننا القول أنّ الروبوت هو دالة تأخذ كائن villageState، وتعيد اسم مكان قريب. لأننا نريد الربوتات أن تكون قادرة على تذكر أشياء بعينها كي تنفِّذ الخطط الموضوعة لها من قِبلنا، فسنمرر إليها ذاكرتها، ونسمح لها بإعادة ذاكرة جديدة، ومن ثم يعيد الروبوت كائنًا يحتوي الاتجاه الذي يريد السير فيه، وقيمة ذاكرة تُعطى إليه في المرة التالية التي يُستدعى فيها. function runRobot(state, robot, memory) { for (let turn = 0;; turn++) { if (state.parcels.length == 0) { console.log(`Done in ${turn} turns`); break; } let action = robot(state, memory); state = state.move(action.direction); memory = action.memory; console.log(`Moved to ${action.direction}`); } } لننظر ما الذي يجب على الروبوت فعله كي "يحل" حالة ما: يجب عليه التقاط جميع الطرود أولًا من خلال الذهاب إلى كل موقع فيه طرد، ثم يسلِّم تلك الطرود بالذهاب إلى كل عنوان من العناوين المرسل إليها هذه الطرود، حيث لا يذهب إلى موقع التسليم إلا بعد التقاط الطرد الخاص به. تُرى ما هي أغبى خطة يمكن أن تنجح هنا؟ إنها العشوائية لا شك، حيث يتخِذ الروبوت اتجاهًا عشوائيًا عند كل منعطف، مما يعني أنه سيمر لا محالة على جميع الطرود بعد عدد من المحاولات، وسيصل كذلك إلى موقع تسليمها في مرحلة ما. انظر: function randomPick(array) { let choice = Math.floor(Math.random() * array.length); return array[choice]; } function randomRobot(state) { return {direction: randomPick(roadGraph[state.place])}; } تعيد Math.random()‎ عددًا بين الصفر والواحد، ويكون دومًا أقل من الواحد، كما يعطينا ضرب عدد مثل هذا في طول أي مصفوفة ثم تطبيق Math.floor عليه موقعًا عشوائيًا للمصفوفة. وبما أنّ هذا الروبوت لا يحتاج إلى تذكر أي شيء، فسيَتجاهل الوسيط الثاني له ويهمل خاصية memory في كائنه المعاد؛ وتذكّر أنّه يمكن استدعاء دوال جافاسكربت بوسائط إضافية دون آثار جانبية مقلقة. نحتاج الآن إلى طريقة لإنشاء حالة جديدة بها بعض الطرود، وذلك من أجل إطلاق هذا الروبوت للعمل، والتابع الساكن -المكتوب هنا بإضافة خاصيةٍ مباشرةً للمنشئ- مكان مناسب لوضع هذه الوظيفة. VillageState.random = function(parcelCount = 5) { let parcels = []; for (let i = 0; i < parcelCount; i++) { let address = randomPick(Object.keys(roadGraph)); let place; do { place = randomPick(Object.keys(roadGraph)); } while (place == address); parcels.push({place, address}); } return new VillageState("Post Office", parcels); }; لا نريد أي طرود مرسلة من المكان نفسه الذي ترسَل إليه، ولهذا تختار حلقة do التكرارية أماكنًا جديدةً في كل مرة تحصل على مكان مطابق للعنوان. دعنا نبدأ عالمًا افتراضيًا، كما يلي: runRobot(VillageState.random(), randomRobot); // → Moved to Marketplace // → Moved to Town Hall // → … // → Done in 63 turns كما نرى من المثال، إذ غيّر الروبوت اتجاهه ثلاثًا وستين مرة، وذلك الرقم الكبير بسبب عدم التخطيط الجيد للخطوة التالية، كما سننظر في هذا قريبًا. يمكنك استخدام دالة runRobotAnimation المتاحة في البيئة البرمجية لهذا المقال، حيث ستنفِّذ المحاكاة، وستعرض لك الروبوت وهو يتحرك في خارطة القرية، بدلًا من إخراج نص فقط. runRobotAnimation(VillageState.random(), randomRobot); سندع طريقة تنفيذ runRobotAnimation مبهمةً في الوقت الحالي، حيث ستستطيع معرفة كيفية عملها بعد قراءة المقال الرابع عشر من هذه السلسلة والذي نناقش فيه تكامل جافاسكربت في المتصفحات. طريق شاحنة البريد لا شك أنّ فكرة الروبوت هذه لتوصيل البريد فكرة بدائية، وأجدر بنا تطوير هذا البرنامج قليلًا، فلم لا ننظر إلى توصيل البريد في العالم الحقيقي لنستوحي منه أفكارًا لعالمنا الصغير؟ أحد هذه الحلول هو البحث عن طريق يمر على جميع الأماكن في القرية، وحينها يأخذ الروبوت هذه الطريق مرتين. انظر مثلًا على هذا الطريق بدءًا من مكتب البريد: const mailRoute = [ "Salma's House", "Cabin", "Salma's House", "Omar's House", "Town Hall", "Sara's House", "Mostafa's House", "Sama's House", "Shop", "Sama's House", "Farm", "Marketplace", "Post Office" ]; نحتاج إلى الاستفادة من ذاكرة الروبوت إذا أردنا استخدام الروبوت المتتبع للطريق route-following، حيث يحذف الروبوت العنصر الأول عند كل منعطف ويحتفظ ببقية الطريق: function routeRobot(state, memory) { if (memory.length == 0) { memory = mailRoute; } return {direction: memory[0], memory: memory.slice(1)}; } سيكون هذا الروبوت بهذا الأسلوب الجديد أسرع من الأسلوب الأول، إذ سيكون أقصى عدد من الاتجاهات التي يسلكها أو المنعطفات التي يأخذها هو 26 -وهو ضعف عدد الأماكن في طريق القرية-، وإن كان في العادة أقل من هذا العدد، فليست جميع الأماكن بها طرود بريد في كل مرة. اكتشاف الطريق Pathfinding لنبحث في طريقة أكثر تطورًا من المرور على جميع الأماكن في القرية في كل مرة، فلا شك في أن الروبوت سيكون أكثر كفاءة إذا عدّل سلوكه ليناسب العمل الحقيقي المراد تنفيذه؛ لذا يجب امتلاكه القدرة على التحرك نحو طرد معين أو موقع تسليم بعينه، وعليه نحتاج دالة لإيجاد الطريق المناسبة. تُعَدّ مشكلة إيجاد الطريق باستخدام مخطط هي مشكلة البحث، حيث نستطيع تحديد ما إذا كان الحل المعطى -أي الطريق- مناسبًا أم لا، لكن لا نستطيع حساب الحل بالطريقة نفسها عند حساب حاصل جمع 2+2 مثلًا، وإنما يجب إنشاء حلولًا محتملةً لإيجاد واحد صالح. تتضح هنا المشكلة أكثر، إذ لا نهايةً لعدد الاحتمالات الممكنة للطرق من خلال مخطط، لكن يمكن تضييق عدد الاحتمالات إذا أردنا الطرق المؤدية من نقطة أ إلى نقطة ب مثلًا، فعندئذ لن يهمنا سوى الطرق التي تبدأ من النقطة أ، كما لا نريد الطرق التي تمر المكان نفسه مرتين، إذ لا تُعَدّ هي الطرق الأكثر كفاءة في أي مكان، ويقلل هذا عدد الطرق التي يجب اعتمادها من قِبَل دالة البحث أكثر وأكثر. نريد في الواقع أقصر طريق فقط، وعليه يجب النظر في الطرق الأقصر أولًا قبل النظر في الطرق الأطول، وأحد الأساليب لفعل ذلك هو بدء طرق من نقطة تحرك الروبوت لتُستكشف جميع الأماكن التي يمكن الوصول إليها ولم يُذهب إليها بعد، حتى تصل إحدى تلك الطرق إلى المكان المراد تسليم الطرد إليه، وهكذا نستكشف الطرق التي يحتمل أن تكون مفيدة لنا، ونتخذ أقصرها أو واحدًا من أقصر تلك الطرق. كما في الدالة التالية: function findRoute(graph, from, to) { let work = [{at: from, route: []}]; for (let i = 0; i < work.length; i++) { let {at, route} = work[i]; for (let place of graph[at]) { if (place == to) return route.concat(place); if (!work.some(w => w.at == place)) { work.push({at: place, route: route.concat(place)}); } } } } يجب أن يتم الاستكشاف بترتيب صحيح، فالأماكن التي يصل إليها أولًا يجب استكشافها أولًا، لكن انتبه إلى أن مكان س مثلًا لا يُستكشف فور الوصول إليه، إذ سيعني هذا أنه علينا استكشاف أماكن يمكن الوصول إليها من س وهكذا، رغم احتمال وجود مسارات أقصر لم تُستكشف بعد. وعلى هذا فإن الدالة تحتفظ بقائمة عمل work list، وهي مصفوفة من الأماكن التي يجب استكشافها فيما بعد مع الطرق التي توصلنا إليها، حيث تبدأ بموقع ابتدائي للبدء منه وطريق فارغة، ثم يبدأ البحث بعدها بأخذ العنصر التالي في القائمة واستكشافه، مما يعني النظر في جميع الطرق الخارجة من هذا المكان، فإن كان أحدها هو الهدف المراد، فيُعاد طريق تامة finished road، وإلا فسيضاف عنصر جديد إلى القائمة إن لم يُنظر في هذا المكان من قبل. كذلك، إن كنا قد نظرنا فيه من قبل، فقد وجدنا إما طريق أطول إلى هذا المكان أو واحدة بنفس طول الطريق الموجودة -وبما أننا نبحث عن الطرق الأقصر أولًا- ولا نحتاج إلى استكشافها عندئذ. تستطيع تخيل هذا بصريًا على أساس شبكة من الطرق المعروفة، حيث تخرج من موقع ابتدائي، وتنمو بانتظام في جميع الجوانب، لكن لا تتشابك مع بعضها أو تنعكس على نفسها؛ وبمجرد وصول خيط من تلك الشبكة إلى الموقع الهدف، فيُتتبَّع ذلك الخيط إلى نقطة البداية ليعطينا الطريق التي نريدها. لا تعالج شيفرتنا الموقف الذي لا تكون فيه عناصر عمل على قائمة العمل، وذلك لعِلمنا باتصال المخطط الخاص بنا، أي يمكن الوصول إلى كل موقع من جميع المواقع الأخرى، وسنكون قادرين دائمًا على إيجاد طريق ممتدة بين نقطتين، فلا يفشل البحث الذي نجريه. function goalOrientedRobot({place, parcels}, route) { if (route.length == 0) { let parcel = parcels[0]; if (parcel.place != place) { route = findRoute(roadGraph, place, parcel.place); } else { route = findRoute(roadGraph, place, parcel.address); } } return {direction: route[0], memory: route.slice(1)}; } يستخدِم هذا الروبوت قيمة ذاكرته على أساس قائمة من الاتجاهات ليتحرك وفقًا لها، تمامًا مثل الروبوت المتتبع للطريق الذي ذكرناه آنفًا، وعليه معرفة الخطوة التالية إذا وجد القائمة فارغة؛ كما ينظر في أول طرد غير مسلَّم في الفئة التي معه، فإن لم يكن قد التقطه، فسيرسم طريقًا إليه، وإن كان قد التقطه، فسينشئ طريقًا إلى موقع التسليم، انظر كما يلي: runRobotAnimation(VillageState.random(), goalOrientedRobot, []); ينهي هذا الروبوت مهمة تسليم خمسة طرود في نحو ستة عشر منعطفًا، وهذا أفضل بقليل من routeRobot، لكن لا زال هناك فرصة للتحسين أكثر من ذلك. تدريبات معايرة الروبوت من الصعب موازنة الروبوتات بجعلها تحل بعض السيناريوهات البسيطة، فلعل أحدها حصل على مهام سهلة دون الآخر. اكتب دالة compareRobots التي تأخذ روبوتين مع ذاكرتهما الابتدائية، وتولد مائة مهمة، ثم اجعل كل واحد من الروبوتين يحل هذه المهام كلها واحدة واحدة، ويجب أن يكون الخرج عند انتهائهما هو العدد المتوسط للخطوات التي قطعها كل واحد لكل مهمة. تأكد من إعطاء المهمة نفسها لكلا الروبوتين في تلك المهام المئة لضمان العدل والدقة في النتيجة، بدلًا من توليد مهام مختلفة لكل روبوت. تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. function compareRobots(robot1, memory1, robot2, memory2) { // شيفرتك هنا } compareRobots(routeRobot, [], goalOrientedRobot, []); إرشادات للحل سيكون عليك كتابة صورة من دالة runRobot، بحيث تعيد عدد الخطوات التي قطعها الروبوت لإتمام المهمة، بدلًا من تسجيل الأحداث في الطرفية. عندئذ تستطيع دالة القياس توليد حالات جديدة في حلقة تكرارية، وعدّ خطوات كل روبوت؛ وحين تولد قياسات كافية، فيمكنها استخدام console.log لإخراج المتوسط لكل روبوت، والذي سيكون ناتج قسمة العدد الكلي للخطوات المقطوعة على عدد القياسات. كفاءة الروبوت هل تستطيع كتابة روبوت ينهي مهمة التوصيل أسرع من goalOrientedRobot؟ ما الأشياء التي تبدو غبيةً بوضوح؟ وكيف يمكن تطويرها؟ إن حللت التدريبات السابقة، فربما تود استخدام دالة compareRobots التي أنشأتَها قبل قليل للتحقق إن كنت قد حسّنت الروبوت أم لا. تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. // شيفرتك هنا runRobotAnimation(VillageState.random(), yourRobot, memory); إرشادات للحل إن القيد الرئيسي لـ goalOrientedRobot هو تعاملها مع طرد واحد في كل مرة، وستمضي ذهابًا وإيابًا في القرية، وذلك لأن الطرد الذي تريده موجود على الناحية الأخرى من الخارطة، حتى لو كان في طريقها طرود أخرى أقرب. أحد الحلول الممكنة هنا هو حساب طرق جميع الطرود ثم أخذ أقصرها، ويمكن الحصول على نتائج أفضل إذا كان لدينا عدة طرق قصيرة، فسنختار حينها الطرق التي فيها التقاط طرد بدلًا من التي فيها تسليم طرد. المجموعة الثابتة ستجد أغلب هياكل البيانات الموجودة في بيئة جافاسكربت القياسية لا تناسب الاستخدام الثابت، حيث تملك المصفوفات التابعَين slice وconcat اللذَين يسمحان لنا بإنشاء مصفوفات جديدة دون تدمير القديمة، لكن Set مثلًا ليس فيه توابع لإنشاء فئة جديدة فيها عنصر مضاف إلى الفئة الأولى أو محذوف منها. اكتب صنف جديد باسم PGroup يشبه الصنف Group من المقال السادس، حيث يخزن مجموعة من القيم، وتكون له التوابع add، وdelete، وhas، كما في الصنف Group تمامًا. يعيد التابع add فيه نسخةً جديدةً من PGroup مع إضافة العضو المعطى given member وترك القديم دون المساس به، وبالمثل، فيجب على التابع delete إنشاء نسخةً جديدةً ليس فيها العضو المعطى. يجب أن يعمل هذا الصنف مع أي نوع من القيم وليس السلاسل النصية فقط، ولا تُشترط كفاءته عند استخدامه مع كميات كبيرة من القيم؛ كذلك ليس شرطًا أن يكون الباني constructor جزءًا من واجهة الصنف رغم أنك تريد استخدام ذلك داخليًا، وإنما هناك نسخة فارغة PGroup.empty يمكن استخدامها على أساس قيمة ابتدائية. لماذا تظن أننا نحتاج إلى قيمة PGroup.empty واحدة فقط بدلًا من دالة تنشئ خارطةً جديدةً وفارغةً في كل مرة؟ تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen. class PGroup { // شيفرتك هنا } let a = PGroup.empty.add("a"); let ab = a.add("b"); let b = ab.delete("a"); console.log(b.has("b")); // → true console.log(a.has("b")); // → false console.log(b.has("a")); // → false إرشادات للحل ستكون أفضل طريقة لتمثيل مجموعة من القيم الأعضاء مصفوفةً لسهولة نسخها. تستطيع إنشاء مجموعةً جديدةً حين تضاف قيمة ما إليها، وذلك بنسخ المصفوفة الأصلية التي فيها القيمة المضافة -باستخدام concat مثلًا-، وتستطيع ترشيحها من المصفوفة حين تُحذف تلك القيمة. يستطيع باني الصنف أخذ مثل هذه المصفوفة على أساس وسيط، ويخزنها على أنها الخاصية الوحيدة للنسخة، ولا تُحدَّث هذه المصفوفة بعدها. يحب إضافة الخاصية empty إلى باني غير تابع بعد تعريف الصنف، مثل وسيط عادي. تحتاج إلى نسخة empty واحدة فقط بسبب تطابق المجموعات الفارغة وعدم تغير نُسَخ الصنف، كما تستطيع إنشاء مجموعات مختلفة عديدة من هذه المجموعة الفارغة دون التأثير عليها. ترجمة -بتصرف- للفصل السابع من كتاب Elequent Javascript لصاحبه Marijn Haverbeke.