الجداء النقطي وارتباطه بطول الأشعة وتعامدها في التصاميم 3D

سنوضّح في هذا المقال حقيقتين مهمتين، أولهما أن الجداء النقطي لمصفوفة عمودية مع نفسها يعطي مربع طول الشعاع الذي تمثله، وثانيهما أن الجداء النقطي لمصفوفتين عموديتين تمثلان شعاعين متعامدين يساوي الصفر.

سنوضح في هذا المقال المواضيع التالية:

الجداء النقطي وطول الشعاع.
شعاع الوحدة Unit Vector.
شعاع الوحدة الناظم Unit Normal.
الجداء النقطي للأشعة المتعامدة ومصفوفاتها العمودية.
كيفية بناء شعاع متعامد مع شعاع معين.
تعريف ميل Slope الخط ثنائي الأبعاد.
العلاقة بين ميول الخطوط المتعامدة ثنائية الأبعاد.

صيغة الجداء النقطي المتعلقة بطول الشعاع

لنفترض أن لدينا ‎v = ( 3, 4 )^T‎، فأوجد ناتج الجداء النقطي v · v وطول الشعاع v:

‎v · v = ( 3, 4 )^T · ( 3, 4 )^T = 3₂ + 4₂ = 9 + 16 = 25 = 5_2‎

طول v ‫= 5 لأنه جزء من المثلث قائم الزاوية 3/4/5.

رأينا في المقال السابق أن الجداء النقطي لشعاع مع نفسه هو:

‎(x, y, z)^‎T · (x, y, z)^T = x² + y² + z²

وتوجد طريقة أخرى لكتابة ذلك وهي:

v · v = | v |^2‎

ناتج الجداء النقطي لمصفوفة عمودية مع نفسها هو عدد حقيقي (مقدار سلمي) Scalar، وهو مربع طول الشعاع الذي تمثله.

ملاحظة: إذا استخدمتَ الإحداثيات المتجانسة Homogeneous Coordinates، فستحتاج هذه العملية الحسابية إلى التعديل بعض الشيء، وتذكّر أن الطول هو خاصية للشعاع الهندسي، وليس خاصية للمصفوفة العمودية التي يمكن استخدامها لتمثيل الشعاع.

لنوجد الآن طول الشعاع الذي تمثله المصفوفة العمودية ‎( 2, 1, -1)^T‎:

ناتج الجداء النقطي هو 4+1+1 = 6، وبالتالي فإن الطول هو ‎√6.

خاصيات الجداء النقطي المتعلقة بطول الشعاع

إليك بعض الخاصيات الجداء النقطي المتعلقة بطول الشعاع:

إذا غيّرتَ حجم شعاع أو ضربته مع عدد حقيقي k، فإنك تضرب طوله بهذه القيمة k:

‎(kv)·(kv) = k² v ² وبالتالي | k v | = k| v |

طول الشعاع الصفري هو صفر:

‎| 0 | = 0

ناتج الجداء النقطي للشعاع الصفري مع أي شعاع آخر هو صفر:

0‎ · v = 0

لا يغيّر عكس اتجاه الشعاع من طوله:

| -v | = | v |

أوجد طول الشعاع ‎(30, 40)^T‎:

‎(30, 40)^T = 10(3, 4)^T‎، وبالتالي يكون الطول 10*5 = 50.

أو يمكنك حسابه بطريقة أصعب كما يلي:

‎|(30,40)|² = 900 + 1600 = 2500

والطول = ‎√2500 ‫= 50

أشعة الوحدة Unit Vectors

تذكّر أن شعاع الوحدة هو شعاع بطول 1، وتسمَّى عملية إنشاء شعاع وحدة له اتجاه الشعاع المُعطَى نفسه بالتوحيد Normalizing التي تُعطَى بالصيغة التالية (كما ناقشنا في مقال سابق):

v_u = v / | v |

تُطبَّق هذه الصيغة على الأشعة والمصفوفات العمودية التي تمثلها، إذ يمكن حساب الطول | v | باستخدام الجداء النقطي للمصفوفات العمودية.

ملاحظة: لاحظ أننا استخدمنا مصطلح "Normal" ، ولكن يجب الانتباه إلى أن لها معانٍ متعددة، إذ يعني مصطلح التوحيد Normalizing إنشاءُ شعاع الوحدة في اتجاه الشعاع الأصلي نفسه، بينما يُطلَق على الشعاع العمودي على سطح معين أحيانًا اسم "الشعاع الناظم Normal Vector"، ولكنه ليس شعاع الوحدة بالضرورة، لذا احرص على ألّا تقول أبدًا "الشعاع الناظم" عندما تقصد "شعاع الوحدة".

إبقاء طول الشعاع صريحًا عند حساب شعاع الوحدة

جرّب إجراء عملية التوحيد للشعاع الذي تمثله المصفوفة العمودية ‎( 1.2, -4.2, 3.5 )^T‎:

ناتج الجداء النقطي هو:

‎( 1.2, -4.2, 3.5 )^T · ( 1.2, -4.2, 3.5 )^T = 1.2² + (-4.2)² + 3.5² = 31.33

ونمثّل شعاع الوحدة كما يلي:

‎( 1.2, -4.2, 3.5 )^T / √31.33. = (0.2144, -0.7504, 0.6253)^T

يجب عليك ترك الإجابة بالصيغة الأولى السابقة دون إجراء عملية القسمة عند الحل بالورقة والقلم، إذ ستوفر لك الحسابات اللاحقة التي ستجريها في كثير من الأحيان فرصة لإلغاء الطول، إذا تركته صريحًا كما في الصيغة الأولى.

تمثيل أشعة الوحدة للاتجاه

أجب عن الاسئلة التالية (قد ترغب في التفكير في الأشعة ثنائية الأبعاد أثناء إجابتك، بالرغم من أن الإجابات ستكون صحيحة بالنسبة للأشعة ثلاثية الأبعاد أيضًا):

كم عدد الأشعة التي يمكن أن تكون في اتجاه معين؟ متعددة بصورة لا نهائية.
كم عدد أشعة الوحدة التي يمكن أن توجد في اتجاه معين؟ شعاع واحد فقط.

يمكن أن يكون هناك عدد لا نهائي من الأشعة في اتجاه معين لأن عناصر الشعاع هي أعداد حقيقية، لذلك يوجد عدد لا نهائي من الأشعة التي تحاذي المحور x في الفضاء ثنائي الأبعاد مثلًا، وتبدو المصفوفات العمودية لهذه الأشعة بالصورة ‎(s, 0)^T‎.

يؤشّر شعاع الوحدة لشعاع معين إلى اتجاه هذا الشعاع نفسه، ولا يوجد سوى شعاع وحدة واحد فقط في اتجاه معين، وتوجد قيمة واحدة فقط للتعبير ‎v / | v |‎، ويوجد شعاع وحدة واحد فقط في اتجاه x الموجب، وتمثله المصفوفة العمودية ‎( +1, 0)^T‎.

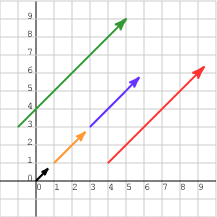
ينطبق الشيء نفسه على المناحي Orientations والأبعاد الأخرى. يظهِر الشكل التالي أشعة لها أطوال مختلفة والمنحى نفسه، ولكن يكون أحدها فقط هو شعاع الوحدة.

تذكّر الصيغة التالية لحساب زاوية الشعاع:

الزاوية = arc tan( y/x )‎

ولكن ليست هذه الصيغة مفيدة جدًا في الفضاء ثلاثي الأبعاد، إذ لا يكفي تحديد الزاوية بين الشعاع وأحد المحاور فقط عندما يكون هناك ثلاثة محاور.

يُستخدَم شعاع الوحدة لشعاع معين في أغلب الأحيان للتعبير عن اتجاه هذا الشعاع، حيث يوجد شعاع وحدة واحد فقط، لذا فإن تعبيره عن الاتجاه فريد من نوعه، وينطبق الشيء نفسه على جميع الأبعاد.

ليكن لدينا الشعاع ‎v = ( -3, 2, 4)^T‎ مثلًا، حيث يمكننا معرفة اتجاهه من خلال حساب شعاع الوحدة كما يلي:

v| v |² = 9 + 4 + 16 = 29
‎v_u = v / √29

الجداء النقطي للأشعة التي بينهما زاوية قائمة

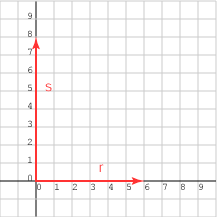
إذا كان لدينا شعاعان موجَّهان بحيث يكون بينهما زاوية مقدارها 90 درجة مثل أن يكون أحدهما يحاذي المحور x والآخر يحاذي المحور y كما في الشكل التالي، فستكون نتيجة جدائهما النقطي هي 0:

إذًا لنوجد الجداء النقطي للشعاعين ‎r = (6, 0)^T‎ و ‎s = (0, 😎^T‎ كما يلي:

‎(6, 0)^T · (0, 😎^T = 6*0 + 0*8 = 0

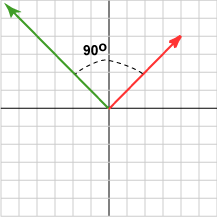
لنفترض أننا دوّرنا الشعاعين السابقين بزاوية 45 درجة كما في الشكل السابق ليصبحا كما يلي (لا تقلق بشأن كيفية تدوير الأشعة، إذ سنوضّحه في مقال لاحق):

r' = ( 6cos(45), 6sin(45) )^T

s' = ( -8sin(45), 8cos(45) )^T

ستبقى الزاوية بينهما بعد تدويرها تساوي 90 درجة، وبالتالي سيكون الجداء النقطي لهما 0 أيضًا.

أوجد الجداء النقطي للشعاعين:

r' = ( 2cos(45), 2sin(45) )^T

s' = ( -3sin(45), 3cos(45) )^T

نطبّق الجداء النقطي كما يلي:

r' · s' = 2cos(45) * (-3)sin(45) + 2sin(45) * 3cos(45) = -2cos(45) * (3)sin(45) + 2sin(45) * 3cos(45) = -6cos(45) * sin(45) + 6cos(45) * sin(45) = 0‎

الجداء النقطي للأشعة المتعامدة

يبدو من المعقول أن يكون حاصل الجداء النقطي لشعاعين هو نفسه بعد تدويرهما بالمقدار نفسه، وبالتالي نستنتج أن الجداء النقطي لشعاعين متعامدين هو صفر، أي أن الجداء النقطي للمصفوفتين العموديتين اللتين تمثلهما هو الصفر.

يهمنا فقط المنحى النسبي، حيث إذا كان الشعاعان متعامدين، فسيكون حاصل الجداء النقطي لهما صفرًا، بغض النظر إن تقاطعا أم لا، إذ ليس من الضروري أن يتقاطع شعاعان ليكونا متعامدين، فمن غير المنطقي التحدث عن تقاطع شعاعين بما أن الأشعة ليس لها موقع محدد، وهذه هي النتيجة نفسها التي رأيناها مع الأشعة الهندسية.

يمكننا القول أن الشعاعين التاليين متعامدان لأن حاصل الجداء النقطي لهما يساوي الصفر:

q = ( -5, 3 )^T‎

r = ( 3, 5 )^T

عدم اعتماد الجداء النقطي للأشعة المتعامدة على الطول

يمكننا تشكيل مصفوفة عمودية ثنائية الأبعاد متعامدة مع مصفوفة أخرى من خلال تبديل العناصر وتغيير إشارة أحدها، ولكن تعمل هذه الطريقة فقط في الفضاء ثنائي الأبعاد، حيث يمكنك العثور على عدد لا حصر له من الأشعة المتعامدة مع شعاع محدَّد مثل الأشعة التالية المتعامدة مع الشعاع ‎( -5, 3)^T‎:

( 3, 5 )^T
( -3, -5)^T
( 1.5, 2.5)^T +( 6, 10)^T
…. وغيرها

إذا كان الشعاع u متعامدًا مع الشعاع v، فإن الجداء النقطي ‎u · v = 0، وبالتالي ‎(k u) · v = k(u · v)= 0 لأي عدد حقيقي k، إذًا هناك عدد لا نهائي من الأشعة (k u‎) المتعامدة مع الشعاع v.

قد نرغب في العثور على شعاع الوحدة الناظم Unit Normal لشعاع معين الذي هو شعاع:

متعامد (ناظم) مع الشعاع المعطى.
يبلغ طوله 1.

ملاحظة: تذكر ألّا تخلط بين مفهومي التوحيد Normalizing (إنشاء شعاع وحدة في اتجاه الشعاع نفسه)، وحساب شعاع الوحدة الناظم (جعل شعاع الوحدة في اتجاه متعامد مع الشعاع).

لنحسب الآن شعاع الوحدة الناظم للشعاع ‎(-5, 3)^T‎:

‎(3, 5)/( √34)‎‎، أو يمكنك اختيار الخيار الآخر: ‎(-3, -5)/( √34)‎.

عدد لا نهائي من الأشعة الناظمة

الأشعة في الفضاء ثلاثي الأبعاد لها أيضًا أشعة وحدة ناظمة، ولكن لا يُعَد شعاع الوحدة الناظم لشعاع معين فريدًا، فمثلًا تكون جميع القضبان متعامدةً مع المحور في عجلة العربة كما في الشكل السابق، أي أنّ جميع الخطوط في مستوي هذه القضبان متعامدة مع المحور، وبالتالي هناك عدد لا نهائي منها.

لنوجد عددًا من الأشعة الناظمة للشعاع الذي تمثله المصفوفة العمودية ‎(1, 2, 2)^T‎ كما يلي:

( 0, 0, 0 )
( -2, 1, 0 )
( 0, -1, 1 )
( -4, 1, 1 )
( 0, 1, -1 )
… وغيرها الكثير بعدد لا نهائي

جميع الأشعة السابقة هي أشعة ناظمة للشعاع المعطى، لأن حاصل الجداء النقطي لكل منها مع هذا الشعاع يساوي الصفر، ولكنها ليست أشعة وحدة، وإن أردتَ إيجاد أشعة الوحدة الناظمة، فسيكون هناك عدد لا نهائي منها أيضًا.

الشعاع الصفري متعامد مع جميع الأشعة

لاحظ الشعاع الناظم الأول الذي هو الشعاع الصفري في المثال السابق، فحاصل الجداء النقطي للشعاع الصفري مع الشعاع المُعطَى هو الصفر، لذلك يجب أن يكون الشعاع الصفري متعامدًا مع هذا الشعاع. تستخدم كتب الرياضيات في أغلب الأحيان حقيقة أن الشعاع الصفري متعامد مع جميع الأشعة (من النوع نفسه)، ولكن لن نحتاج إلى هذه الحقيقة حاليًا، بل يمكن أن نحتاجها في المقالات اللاحقة. طول الشعاع الصفري هو صفر، لذا فهو ليس شعاع وحدة ناظم.

قد تتذكر من مادة الهندسة التحليلية الصيغة التالية لميل خطٍ في فضاء ثنائي الأبعاد وغير موازٍ للمحور Y:

m‎‎ = (التغير في قيمة y) / (التغير في قيمة x)

هذه هي الصيغة نفسها المُستخدَمة في ظل الزاوية مع المحور x، وترتبط هذه الصيغة بالسبب الذي يجعل الجداء النقطي للأشعة المتعامدة ثنائية الأبعاد يساوي صفرًا.

ميول الخطوط المتعامدة

لنحاول الإجابة على الأسئلة التالية:

ما هو الميل m₁‎ للشعاع ‎( 2, 5 )^T‎؟ m₁ = 5/2
ما هو الميل m₂‎ للشعاع ‎( -5, 2 )^T‎؟ m₂ = -2/5
ما هو ناتج الجداء النقطي لهما؟

‎(2)(-5) + (5)(2) = 0

ما هو ناتج ضرب m₁‎ و m₂‎؟

5/2‎ * -2/5 = -1

قد تتذكر الحقيقة التالية من دروس الرياضيات السابقة:

إذا كان المستقيمان متعامدين فإن حاصل ضرب ميليهما يساوي ‎-1.

إليك ما يحدث عندما ننشئ شعاعًا ناظمًا لشعاع ثنائي الأبعاد من خلال تبديل العناصر وتغيير إشارة أحدها:

إذا كان ‎v = ( x, y )^T‎.
فإن الشعاع المعامد له هو ‎v' = ( -y, x )^T‎.
لأن الجداء النقطي ‎( x, y)^T · ( -y, x )^T‎ هو ‎-xy + yx = 0.
ميل الشعاع ‎( x, y )^T‎ هو y/x.
ميل ‎( -y, x )^T‎ هو ‎-x/y.
حاصل ضرب الميلين هو: y/x * -x/y = -(xy)/(xy) = -1.

إذًا هل يُعَد الشعاعان ‎( -1.5, 6)^T‎ و ‎(2, 2)^T‎ متعامدين؟ لا، لأن ناتج الجداء النقطي لهما هو ‎-3 + 12 = 9. ناتج الجداء النقطي ليس صفرًا، لذا فإن الشعاعين ليسا متعامدين، وقد توصّلنا إلى هذه النتيجة بغض النظر عن الأطوال، إذ يمكن اكتشاف تعامد الأشعة بغض النظر عن طولها.

وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على علاقة الجداء النقطي للأشعة مع طولها وتعامدها، وسنناقش في المقال التالي الجداء النقطي غير الصفري لشعاعين.

ترجمة -وبتصرُّف- للفصل Length and the Dot Product من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.