يمكن ضرب المصفوفة بمصفوفة عمودية إذا كانت أبعادهما تسمح بذلك، حيث يُعَد ذلك عمليةً أساسيةً في الرسوميات الحاسوبية وفي العديد من المجالات الأخرى؛ إذ تُجرَى هذه العملية ملايين المرات في الثانية عند تشغيل برنامج الرسوميات ثلاثية الأبعاد.
سنوضح في هذا المقال المواضيع التالية:
- أبعاد معامَلات ونتيجة ضرب المصفوفات بمصفوفة عمودية.
- أبعاد معامَلات ونتيجة ضرب مصفوفة سطرية بالمصفوفات.
- ضرب المصفوفات بمصفوفة عمودية.
- ضرب مصفوفة سطرية بالمصفوفات.
- استخدام الجداء النقطي لضرب المصفوفات.
- الوصول إلى نتيجة ضرب المصفوفات من خلال تطبيق عمليات متعددة من الجداء النقطي.
- قلب Flipping المصفوفة العمودية عند ضرب المصفوفات بمصفوفة عمودية.
- قلب أعمدة المصفوفة عند ضرب مصفوفة سطرية بها.
- التعريفات الرياضية لعمليات ضرب المصفوفات وخطوات تنفيذها.
- الخاصية غير التبديلية لضرب المصفوفات.
رأينا مسبقًا عمليات شبيهة بالضرب، والتي هي:
- ضرب عدد حقيقي (مقدار سلمي) Scalar بعدد حقيقي، والذي يعطي عددًا حقيقيًا.
- ضرب مصفوفة عمودية بعدد حقيقي، والذي يعطي مصفوفة عمودية.
- الجداء النقطي Dot Product للمصفوفات العمودية، والذي يعطي عددًا حقيقيًا.
ضرب المصفوفات بالمصفوفة العمودية
ناتج ضرب مصفوفةٍ ما بمصفوفة عمودية هو مصفوفة عمودية كما في المثال التالي:
سنشرح لاحقًا تفاصيل كيفية تطبيق هذه العملية، ولكن لاحظ الآن أبعاد معامَلات العملية ونتيجتها؛ إذ يمكن تشكيل عملية ضرب مصفوفة بمصفوفة عمودية إذا كان عدد أعمدة المصفوفة مساويًا لعدد أسطر المصفوفة العمودية كما يلي:
Matrix(R x N) x Col. Matrix(N x 1) = Resulting Col. Matrix(R x 1)
يمكن توضيح ذلك في المثال التالي:
Matrix(2 x 2) x Col. Matrix(2 x 1) = Resulting Col. Matrix(2 x 1)
نعرض الأبعاد بالشكل: "Row x Column" (بحيث يكون Row هو عدد الصفوف وColumn هو عدد الأعمدة)، إذ تكون المصفوفة التي أبعادها R x 1 مصفوفةً عمودية، لأنها تحتوي على عمود واحد.
لاحظ أيضًا كيف تكون أبعاد نتيجة ضرب مصفوفة بمصفوفة عمودية في المثال التالي:
Matrix(5 x 5) x Col. Matrix(5 x 1) = Resulting Col. Matrix(5 x 1)
لنحدّد الآن ما إذا كان من الممكن ضرب مصفوفةٍ بمصفوفة عمودية وما هي أبعاد نتيجة عملية الضرب في الأمثلة الموجودة في الجدول التالي:
| أبعاد المصفوفة | أبعاد المصفوفة العمودية | أبعاد النتيجة |
|---|---|---|
| الأبعاد 3 x 3 | الأبعاد 3 x 1 | الأبعاد 3 x 1 |
| الأبعاد 3 x 2 | الأبعاد 2 x 1 | الأبعاد 3 x 1 |
| الأبعاد 2 x 3 | الأبعاد 2 x 1 | غير ممكنة |
| الأبعاد 4 x 3 | الأبعاد 3 x 1 | الأبعاد 4 x 1 |
| الأبعاد 3 x 5 | الأبعاد 5 x 1 | الأبعاد 3 x 1 |
لاحظ أنه من غير الممكن تشكيل عملية الضرب التي تبدو كما يلي:
Matrix(2 x 1) x Col. Matrix(2 x 2) = Resulting Col. Matrix(غير ممكنة)
وضع المصفوفة العمودية على الجهة اليمنى فقط من عملية الضرب
إذا ضربنا مصفوفةً مستطيلةً بمصفوفة عمودية، فستكون المصفوفة العمودية دائمًا على يمين المصفوفة المستطيلة؛ إذ لا يمكن ضربهما إّلا إذا كان "البعد الداخلي Inner Dimension" (البعد M مثلًا) لكل مصفوفة متساويًا:
Matrix(N x M) x Col. Matrix(M x 1) = Resulting Col. Matrix(N x 1)
حيث يمكن تشكيل عملية الضرب التي تبدو كما يلي:
Matrix(1 x 2) x Col. Matrix(2 x 1) = عدد حقيقي(1 x 1)
استخدام الجداء النقطي لضرب المصفوفات
يبدو استخدام الجداء النقطي لضرب المصفوفات ممكنًا من خلال النظر إلى الأبعاد المصفوفات، ولكنه ليس دليلًا على إمكانية ذلك. إليك المثال التالي:
قد يبدو غريبًا بعض الشيء عَدُّ العدد الحقيقي (المقدار السلمي Scalar) كائنًا أبعاده "1 × 1"، ولكن تبقي هذه الطريقة الأمور متناسقةً فيما بينها. لاحظ أن هذا المثال يشبه الجداء النقطي (وهو كذلك فعلًا)، وبالتالي ستتشكّل عملية الضرب كما يلي:
إذًا لنوجد الآن ناتج عملية الضرب التالية كما يلي:
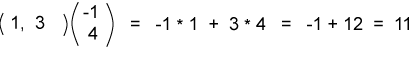
قلب المصفوفة العمودية
من المفيد التفكير في "قلب" المصفوفة العمودية عند تشكيل الجداء النقطي ليحاذي كل صف من المصفوفة، ثم ضرب وجمع العناصر المتقابلة كما في المثال التالي:
وفي المثال التالي أيضًا:
لنشكّل الآن عملية الضرب التالية:
تدريب عملي
اُحسب الجداء النقطي في الجدول التالي. ستجد ناتج الجداء في عمود النتيجة:
| المعامل الأول | المعامل الثاني | النتيجة |
|---|---|---|
المصفوفة 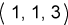
|
المصفوفة العمودية |
الناتج -2 |
المصفوفة 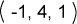
|
المصفوفة العمودية 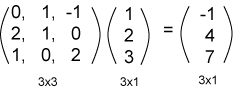
|
الناتج -2 |
المصفوفة 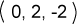
|
المصفوفة العمودية |
الناتج 2 |
سنستخدم عمليات الجداء النقطي السابقة لإيجاد نتيجة ضرب المصفوفة بالمصفوفة العمودية كما يلي:
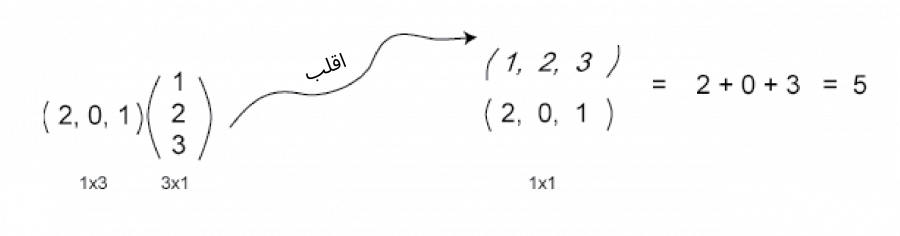
إذًا يمكننا الحصول على ناتج عملية ضرب مصفوفةٍ بمصفوفة عمودية من خلال تطبيق الجداء النقطي للمصفوفة العمودية مع كل صف من المصفوفة الأخرى، ولكن يجب أن تسمح أبعاد كل معامَل بذلك؛ إذ يساعد ذلك على قلب المصفوفة العمودية، بحيث يمكن محاذاة عناصرها مع عناصر المصفوفة كما يلي:
اقلب المصفوفة العمودية واحسب النتيجة ما يلي:
إليك أيضًا بعض عمليات الضرب الأخرى التي قد ترغب في التدرب عليها، ولكن تذكّر أن تقلب المصفوفة العمودية وتضعها فوق المصفوفة، ثم طبّق الجداء النقطي للمصفوفة العمودية التي قلبناها مع صف واحد من المصفوفة في كل مرة:
| العملية | النتيجة |
|---|---|
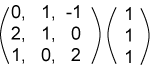
|
الناتج |
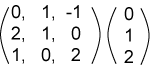
|
الناتج 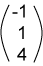
|
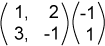
|
الناتج 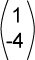
|
استخدام عمليات متعددة من الجداء نقطي لإجراء عملية ضرب المصفوفة السطرية بالمصفوفات
جرّب الآن إجراء العملية التالية:
لاحظ أن أبعاد المصفوفات متوافقة، لذا يمكن إجراء العملية كما يلي:
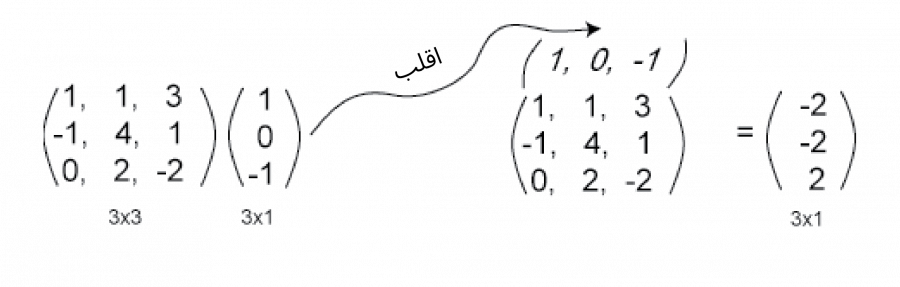
يمكنك أن ترى من المثال السابقة أنه يمكن إجراء عملية ضرب مصفوفةٍ سطرية بمصفوفةٍ ما من خلال تطبيق عدة عمليات جداء نقطية، ولكن يجب قلب أعمدة المصفوفة في هذه الحالة كما يلي:
وضع المصفوفة السطرية على الجهة اليسرى من عملية الضرب
لا يمكن إجراء النوع التالي من عمليات الضرب، لأن الأبعاد غير صحيحة:
Matrix (3 x 4) x Row Matrix (1 x 3)
إذًا يجب أن تكون المصفوفة السطرية على الجهة اليسرى عند ضرب مصفوفة سطرية بمصفوفة مستطيلة، حيث تكون أبعاد المعامَلات والنتيجة كما يلي:
Row Matrix (1 x M) x Matrix (M x C) = Result Row Matrix (M x C)
ملاحظة: المصفوفة التي أبعادها 1xC هي مصفوفة سطرية مكوَّنة من عددٍ "C" من الأعمدة.
نوضّح في الأمثلة الموجودة في الجدول التالي ما إذا كانت عملية الضرب ممكنة وما هي أبعاد نتيجة العملية:
| المعامل الأول | المعامل الثاني | النتيجة |
|---|---|---|
| 3 x 3 | 3 x 1 | 3 x 1 |
| 1 x 2 | 2 x 2 | 1 x 2 |
| 1 x 2 | 2 x 3 | 1 x 3 |
| 4 x 4 | 3 x 1 | غير ممكنة |
| 1 x 5 | 5 x 3 | 1 x 3 |
لنحاول الآن إجراء عملية الضرب التالية:
وينتج ما يلي:
التعريفات الدقيقة لعمليات الضرب
قد تشعر بعدم الارتياح عند تعريف العمليات الرياضية بهذه الطريقة غير الرسمية، لذا إليك بعض التعريفات الأدق:
- ضرب مصفوفة بمصفوفة عمودية Matrix times Column Matrix: ليكن لدينا المصفوفة A التي أبعادها M x C، والمصفوفة العمودية x التي أبعادها C x 1، ويكون ناتج الجداء Ax مصفوفة عمودية أبعادها M x 1؛ إذ يتشكّل عنصرها i من ناتج الجداء النقطي للصف i من المصفوفة A مع المصفوفة العمودية x.
- ضرب مصفوفة سطرية بمصفوفة: ليكن لدينا المصفوفة السطرية x التي أبعادها 1 x R والمصفوفة **A التي أبعادها R x M، ويكون ناتج الجداء *xA* مصفوفة سطرية أبعادها 1 x M، حيث يتشكّل عنصرها الأول من ناتج الجداء النقطي للمصفوفة السطرية x مع العمود i من المصفوفة A.
لنحاول الآن إجراء عملية الضرب التالية:
وسينتج لدينا ما يلي:
خطوات إجراء عملية ضرب المصفوفات
يتضمن الضرب دائمًا عمليات جداء نقطية للصفوف الموجودة على اليسار والأعمدة الموجودة على اليمين وفقًا للتعريفات السابقة، لذا يجب اتباع الخطوات التالية لإجراء أيٍّ من هذه الحسابات:
-
دراسة أبعاد معاملات عملية الضرب حيث:
- يجب أن تكون الأبعاد الداخلية متساوية: 1xN و NxC.
- نتجاهل الأبعاد الداخلية للعثور على أبعاد النتيجة: 1xC.
- نكتب مصفوفة فارغة بالأبعاد الصحيحة لتمثّل المصفوفة الناتجة.
-
ملء جميع عناصر المصفوفة الناتجة كما يلي:
- نقلب كل عمود موجود على اليمين إلى صف على اليسار.
- ينتج كل عنصر من عناصر المصفوفة الناتجة عن عملية جداء نقطي.
تدريب عملي
لا تُعَد Ax و xA متساويتين؛ فإذا كان تطبيق عملية الضرب Ax ممكنة، فستكون أبعاد xA غير متوافقة عند ذلك، ويمكن في بعض الأحيان تشكيل كلٍّ من هاتين العمليتين، ولكن النتائج ستكون مختلفة، وبالتالي يمكن القول أن ضرب المصفوفات ليست عمليةً تبديلية.
إذًا لنختبر مهاراتك في الأمثلة التالية:
| العملية | النتيجة |
|---|---|
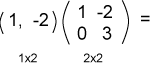
|
الناتج 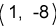
|
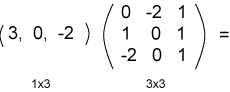
|
الناتج 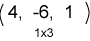
|
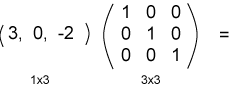
|
الناتج 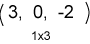
|
وصلنا إلى نهاية هذا المقال الذي تعرّفنا من خلاله على ضرب مصفوفة بمصفوفة عمودية وضرب مصفوفة سطرية بمصفوفةٍ ما، وسنتعرّف في المقال التالي على كيفية ضرب مصفوفة مستطيلة بمصفوفة أخرى.
ترجمة -وبتصرُّف- للفصل Matrix-Column Matrix Multiplicaton من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.


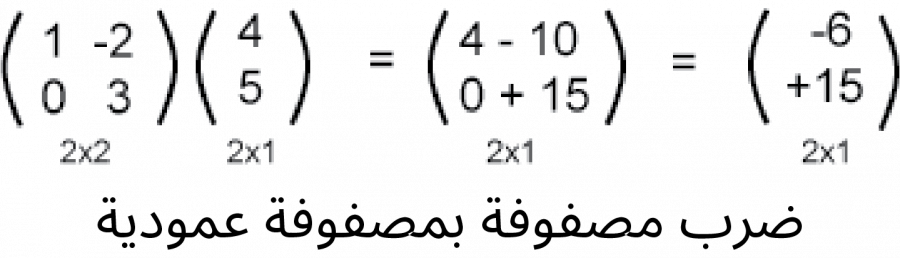
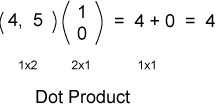
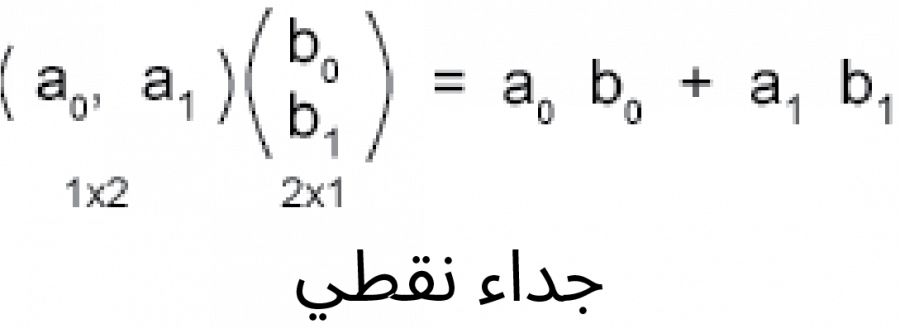
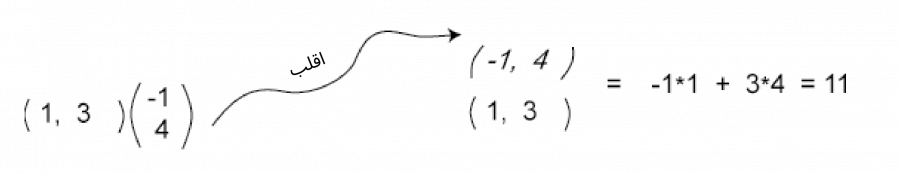
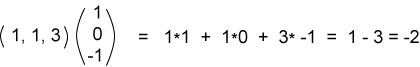
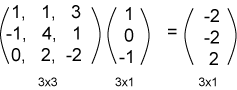
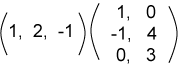
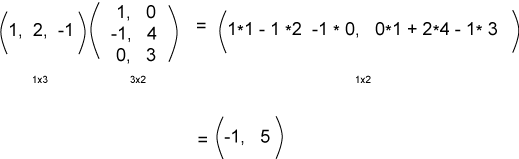
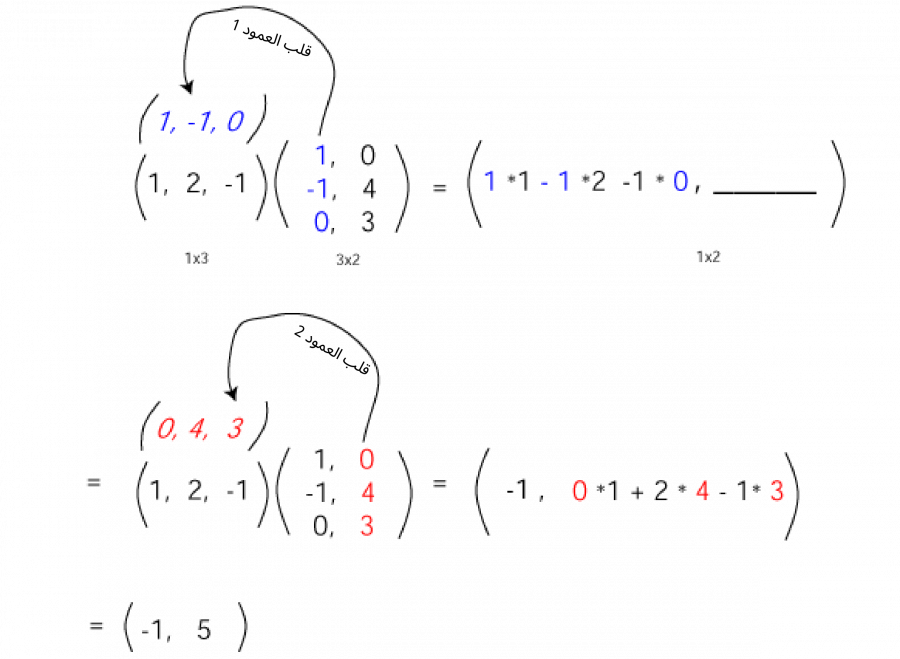
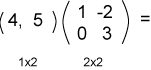
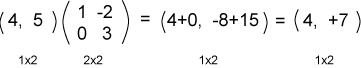
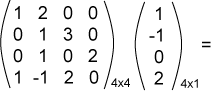
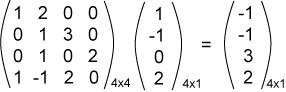











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.