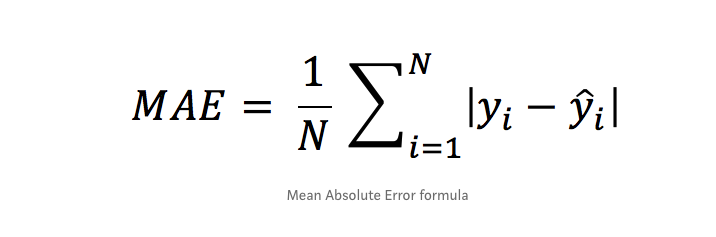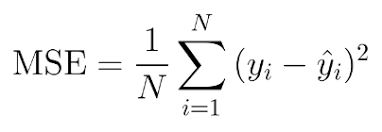Ali Haidar Ahmad

يمكنك ذلك بالطريقة التالية باستخدام مكتبة Json: import json with open('data.json') as file: data = json.load(file) type(data) # Output: dict data.keys() # Output: dict_keys(['key1', 'key2', 'key3', 'key4', 'keyn']) أو باستخدام مكتبة pandas وهنا سيقرأها ك DataFrame: import pandas as pd df = pd.read_json(‘data.json’) print(df)

هو أحد الطرق لتقسيم البيانات بدلا من استخدام train_test_split ويستخدم في حالة كانت البيانات قليلة. import numpy as np from sklearn.model_selection import KFold قمنا باستدعاء المكتبة numpy لتشكيل داتا مزيفه واستدعاء الوظيفه KFold من الوحدة model_selection في مكتبة sklearn #تكوين داتا مزيفة مكونة من أرقام عشوائية: X = np.random.random((1,15)).reshape((5, 3)) y = np.random.random((5,1)) في السطرين السابقين تم تشكيل X ,y كداتا مزيفه (أرقام عشوائيه )حيث X أبعادها 5 أسطر مع ثلاث أعمده وتحوي أرقام عشوائيه أما y عمود واحد بخمس أسطر وتحوي أرقام عشوائية #تقسيم الداتا المزيفه إلى أجزاء : لكن بداية سنعرض الصيغة العامة للتابع: sklearn.model_selection.KFold(n_splits=5, shuffle=False, random_state=None) الوظيفة KFold تأخذ البارمترات التالية: البارمتر الأول n_splits عدد صحيح لتحديد عدد الأجزاء folds وهي افتراضية في sklearn من 3 إلى 5. البارمتر الثاني shuffle متحول بولياني يأخذ True لكي يتم خلط الداتا قبل عملية التقسيم أي جعلها عشوائية ويأخذ False عندما لا نريد خلط الداتا. randomstate: للتحكم بعملية الخلط. وقد تحدثت عنه في هذا الرابط: الأن في مثالنا تم تقسيم الداتا إلى 5 أجزاء مع خلط الداتا قبل عملية التقسيم. وللوصول إلى كل جزء وما يحوية لديك الأسطر التالية حيث يتم استخدام اثنين من الاندكسات في الحلقة للمرور على التدريب والاختبار وتحوي kf.split(X) هذه الاندكسات لكل محاولة من المحاولات يقصد بالمحاولات اي عملية التقسيم المختلفة التي ذكرناها سابقاً بعد ذلك في كل مرور على الحلقة يتم طباعة الاندكس الخاص بالتدريب والاختبار وبعد ذلك تم تخزين بيانات التدريب والاختبار وبعدها طباعة الابعاد لكل منها في كل محاولة. # المثال: #استدعاء المكتبات import numpy as np from sklearn.model_selection import KFold #تكوين داتا مزيفة مكونة من أرقام عشوائية X = np.random.random((1,15)).reshape((5, 3)) y = np.random.random((5,1)) #تقسيم الداتا المزيفه إلى أجزاء kf = KFold(n_splits=2, random_state=44, shuffle =True) #KFold Data for train_index, test_index in kf.split(X): print('Train Data is : \n', train_index) print('Test Data is : \n', test_index) print('-------------------------------') X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print('X_train Shape is ' , X_train.shape) print('X_test Shape is ' , X_test.shape) print('y_train Shape is ' ,y_train.shape) print('y_test Shape is ' , y_test.shape) print('========================================')

هو معيار لقياس كفاءة نماذج التصنيف Classification. يعتمد على حساب عدد مرات اللاتطابق بين القيم الحقيقية والقيم المتوقعة. يمكن تطبيقه باستخدام مكتبة Sklearn كالتالي: sklearn.metrics.zero_one_loss(y_true, y_pred, normalize=True) الوسيط الأول والثاني يمثلان القيم الحقيقية والمتوقعة على التوالي. الوسيط الأخير في حال ضبطه على True سيعيد عدد مرات اللاتطابق كقيمة عشرية. في حال ضبطه على False يعيد عدد مرات اللاتطابق. المثال يوضح: from sklearn.metrics import zero_one_loss y_pred = [1, 0, 2, 1] y_true = [1, 0, 3, 1] z1=zero_one_loss(y_true, y_pred,normalize=True) print(z1) # 0.25 z2=zero_one_loss(y_true, y_pred, normalize=False) # print(z2) # 1 # Machine Learning is everywhere # Written by Ali Ahmed

يحاول الانحدار الخطي LinearRegression نمذجة العلاقة بين متغيرين X وY من خلال ملاءمة معادلة خطية (خط مستقيم) للبيانات التي يتم التدريب عليها وهو من الشكل Y=WX+b. ويستخدم في مهام التنبؤ Regression (مثل توقع أسعار المنازل مثلاُ أو توقع عدد الإصابات بمرض معين). ندعو X بال features و b بال bias (وهي تكافئ الإزاحة) بينما w تمثل أوزان النموذج (وهي تكافئ ميل المستقيم). نميز نوعين للتوقع الخطي: Univariate Linear Regression : أي التوقع الخطي الذي يعتمد فيه الخرج Y على One feature أي تكون X عبارة عن متغير واحد. Multiple linear regression : أي التوقع الخطي الذي يعتمد فيه الخرج Y على أكتر من feature أي تكون X عبارة عن x1,x2,...,xn. يمكن تطبيق التوقع الخطي عن طريق مكتبة Sklearn. يتم استخدامها عبر الموديول .linear_model.LinearRegression sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None) الوسطاء: fit_intercept: لجعل المستقيم يتقاطع مع أفضل نقطة على المحور العيني y. copy_X: وسيط بولياني، في حال ضبطه على True سوف يأخذ نسخة من البيانات ، وبالتالي لاتتأثر البيانات الأصلية بالتعديل، ويفيدنا في حالة قمنا بعمل Normalize للبيانات. normalize: وسيط بولياني، في حال ضبطه على True سوف يقوم بتوحيد البيانات (تقييسها) اعتماداً على المقياس L2norm. وقد سبق وتحدثت عن هذا الموضوع في هذا الرابط: n_jobs: لتحديد عدد العمليات التي ستتم بالتوازي (Threads) أي لزيادة سرعة التنفيذ، افتراضياُ تكون قيمته None أي بدون تسريع، وبالتالي لزيادة التسريع نضع عدد صحيح وكلما زاد العدد كلما زاد التسريع (التسريع يتناسب مع قدرات جهازك)، وفي حال كان لديك GPU وأردت التدريب عليها فقم بضبطه على -1. أهم ال attributes: _coef: الأوزان التي حصلنا عليها بعد انتهاء التدريب وهي مصفوفة بأبعاد (,عدد الfeatures). أهم التوابع: fit(data, truevalue): للقيام بعملية التدريب. predict(data): دالة التوقع ونمرر لها البيانات وتعطيك التوقع لها. score(data, truevalue): لمعرفة مدي كفاءة النموذج ونمرر لها بيانات الاختبار والقيم الحقيقية لها فيقوم بعمل predict للداتا الممررة ثم يقارنها بالقيم الحقيقية ويرد الناتج حسي معيار R Squaerd . إليك التطبيق العملي: الداتاسيت هي مواصفات منازلX مع أسعارها Y في مدينة بوسطن. from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression # تحميل الداتاسيت BostonData = load_boston() x = BostonData.data y = BostonData.target # تقسيم الداتا إلى عينة تدريب وعينة اختبار X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=33, shuffle =True) #تعريف LinearRegressionModel LR = LinearRegression(fit_intercept=True,copy_X=True,n_jobs=-1) LR.fit(X_train, y_train) print('Train Score is : ' ,LR.score(X_train, y_train)) # R Squaerd on trainset print('Test Score is : ' , LR.score(X_test, y_test)) # R Squaerd on testset print('Coef is : \n' , LR.coef_) # Coefficent # حساب القيم المتوقعة y_pred = LR.predict(X_test) print(y_pred[0:10]) # عرض القيم الحقيقية print(y_test[0:10]) # Machine Learning is everywhere

هي دوال تتألف من سطر واحد تستخدم الكلمة المفتاحية lambda على عكس التوابع الأخرى في بايثون التي تستخدم def ككلمة مفتاحية وهي تقوم بإرجاع قيمة عند استدعاءها لها الشكل التالي: lambda [arg1 [,arg2,.....argn]]:expression الكلمة المفتاحية lambda أسماء متحولات الدخل ويوجد فاصلة بين كل متحول وأخر [arg1 [,arg2,.....argn]] ب expression تتم العمليات على المتحولات مثال بسيط لجمع عددين باستخدام Anonymous Function: T=lambda x,y:x+y على عكس التوابع الأخرى التي تستدعى بالاسم فإن Anonymous Function يتم إسنادها لمتغير ومن ثم يكون المتغير هو الاسم لهذا التابع أي يكون الاستدعاء كالتالي: T(2,3) #output:5

يمكن استخدام الوظيفة shuffle من المكتبة random كالأتي: from random import shuffle x = [1,2,3,4,5,6,7,8,9] # تعريف القائمة shuffle(x) # خلط القائمة print(x) #output :[3, 5, 7, 9, 1, 4, 8, 2, 6]

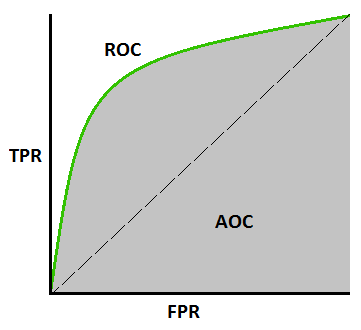
ROC&AUC Score ROC (Receiver Operating Characteristics)curve AUC (Area Under The Curve) ROC&AUC Score: هو معيار لقياس كفاءة نماذج التصنيف. للفهم جيداً يجب أن يكون لديك معرفة حول Recall(Sensitivity) و Precision(Specificity) وقد أشرت لهما سابقاً في هذا الرابط: https://academy.hsoub.com/questions/15466-حساب-ال-precision-و- recall-باستخدام-مكتبة-scikit-learn/ في الصورة المرفقة رسم بياني يعبر عن ROC&AUC ، بحيث : أولاً: <<TPR (True Positive Rate) or Recall or Sensitivity>> يمثل المحور العمودي، ويساوي إلى TP/(TP+FN) ويعبر عن ال Recall أي ال Sensitivity. ثانياً: <<FPR(False Positive Rate)>> ويساوي إلى FP/(FP+TN) أي أنه متمم ال Specificity أي : FPR=1-Specificity. ثالثاً: ROC: يمثل المنحنى الاحتمالي الذي يعبر عن العلاقة بين المحورين. رابعاً: AUC هو المساحة تحت المنحنى ويعبر عن درجة قدرة النموذج على الفصل بين الفئات Classes. ستلاحظ في الأكواد التالية أن زيادة المساحة تحت المنحني تشير إلى أداء أقوى للنموذج. مناقشة القيم أو قراءة القيم: كلما كانت درجة AUC أكبر كلما كان النموذج أفضل علماً أن أعلى قيمة لها 1 وأقل قيمة 0. في حال كانت قيمة AUC=1 فهذا يعني أن النموذج قادر على الفصل بين الClasses بنسبة 100%. الكود رقم 1 يعبر عن هذه الحالة. AUC=0.5 فهذا يعني أن النموذج غير قادر على الفصل بين ال Classes اطلاقاً وهي حالة سيئة، وفيه يكون النموذج غير قادر على إعطاء قرار، أي مثلا في مهمة تصنيف صور القطط والكلاب تشير قيمة 0.5 لل AUC إلى أن النموذج سيقف حائراً أمام أي صورة أي كأن يقول أن هذه الصورة هي 50% كلب و 50% قط. الكود رقم 2 يعبر عن هذه الحالة. AUC=0 فهذا يعني أن النموذج يتنبأ بشكل عكسي بالقيم أي يتموقع أن الأصناف الإيجابية سلبية والعكس بالعكس أي يقول عن القط كلب والكلب قط وبكل ثقة. الكود رقم 3 يعبر عن هذه الحالة. الشكل العام للتابع الذي يقوم بحساب ROC في Sklearn: sklearn.metrics.roc_curve(y_true, y_score) الوسيطين الأول والثاني يعبران عن القيم الحقيقية والمتوقعة على التوالي. يرد التابع 3 قيم fpr و tpr والعتبة وسنستخدم هذه القيم لحساب درجة AUC. الشكل العام للتابع الذي يقوم بحساب AUC في Sklearn: sklearn.metrics.auc(fpr, tpr) قم بتجريب الأكواد التالية لتحصل على الخرج وترى الفروقات: # الكود 1 ############################# Case 1 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([1 , 1 , 0 , 1, 1]) y_pred = np.array([0.99 ,0.02 ,0.01, 0.99,0.999]) #لاحظ نسبة التطابق fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) # طباعة قيم الخرج # لرسم المنحنى plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) # حساب قيمة AUC print('AUC Value : ', AUC) # طباعة القيمة #الكود 2 ############################# Case 2 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([0 ,1 ,0 ,1,0]) y_pred = np.array([0.5 ,0.5 ,0.5, 0.5, 0.5]) # لاحظ أننا غيرنا القيم fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) print('AUC Value : ', AUC) # الكود 3 ############################# Case 3 ######################################## # استيراد المكتبات اللازمة from sklearn.metrics import roc_curve from sklearn.metrics import auc import matplotlib.pyplot as plt import numpy as np # بفرض لدي القيم الحقيقية والمتوقعة التالية y = np.array([0 ,1 ,0 ,0,0]) y_pred = np.array([0.9 ,0.1 ,0.9, 0.9, 0.9]) fpr, tpr, threshold = roc_curve(y,y_pred) print('TPR'+str(tpr)+'\n'+'FPR'+str(fpr)+'\n'+'threshold'+str(threshold)) plt.plot(fpr, tpr) plt.title('ROC curve') plt.xlabel('False Positive Rate (1 - Specificity)') plt.ylabel('True Positive Rate (Sensitivity)') plt.grid(True) AUC = auc(fpr, tpr) print('AUC Value : ', AUC)

ملاحظة إضافية: Precision تسمى أيضاً Specificity Recall تسمى أيضاً Sensitivity والعلاقة بينهما عكسية أي أن زيادة أحدهما تعني نقصان الآخر. وهدفنا يكون الحصول على أعلى قيم لهما دوماً، لذلك يجب الموازنة (Trade off) بين قيمهما.

المشكلة أنك لم تقم بوضع شرط توقف على الاستدعاء العودي وبالتالي تدخل في تكرار لانهائي من الاستدعائات حتى تمتلئ الذاكرة فيظهر لك الخطأ. مثال: هنا عرفنا تابع يقوم بحساب العاملي لعدد ما اعتماداً على العودية. def factorial(x): if x == 1: # عملياً هنا سوف يتوقف الاستدعاء العودي return 1 else: return (x * factorial(x-1)) # هنا يتم الاستدعاء العودي print("The factorial of", 8, "is", factorial(8)) مثال: # تابع تمرر له عدد ويقوم بتصفيره def RecursiveFunction (y): y=y-1 return RecursiveFunction(y); # وبالتالي لم نضع شرط توقف RecursiveFunction (10) # هنا سيستمر الاستدعاء إلى مالانهاية وبالتالي تمتلئ الذاكرة ويتوقف البرنامج ############################ التصحيح بأن نضع شرط توقف ################ def RecursiveFunction (y): if y==0: return "Done" y=y-1 return RecursiveFunction(y); # وبالتالي لم نضع شرط توقف RecursiveFunction (10) # هنا سيستمر الاستدعاء إلى مالانهاية وبالتالي تمتلئ الذاكرة ويتوقف البرنامج أي يجب دوماً وضع شرط يتم من خلاله إيقاف الاستدعاء العودي.

هما معياران لقياس كفاءة نماذج التصنيف Classifications. أولاً: Precision هو نسبة (المتوقع) الإيجابي الصحيح على نسبة (((المتوقع))) الإيجابي الكلي ويعبر عنه بالعلاقة التالية: Precision = TP/(TP+FP) لاحظ أن البسط يعبر عن كل العينات التي قال عنها نموذجنا أنها P وهي بالغعل P. لاحظ أن المقام (TP+FP) يشير إلى كل العينات التي اعتبرها نموذجنا P سواءاً أكان التوقع صحيح أم لا. ويمكن أن نعبر عنه بالصيغة؟ كم هي عدد العينات التي توقع النموذج أنها + وكانت بالفعل + من بين كل التوقعات التي توقع أنها +. لتطبيقه باستخددام scikit-learn نستخدم الصيغة التالية: sklearn.metrics.precision_score(y_true, y_pred) مثال: from sklearn.metrics import precision_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج precision=precision_score(y_true, y_pred) # لطباعة الناتج كنسبة مئوية print(str(precision*100)+'%',sep='') ثانياً: Recall هي كل (التوقعات) الإيجابية الصحيحة مقسومة على العدد الكلي للحالات الإيجابية. Recall = TP/(TP+FN) البسط لم يتغير. المقام تم استبدال FP ب FN ليصبح (TP+FN) ويشير إلى عدد العينات الإيجابية كلها التي اكتشفها النموذج والتي لم يكتشفها أصلاً. sklearn.metrics.recall_score(y_true, y_pred) مثال: from sklearn.metrics import recall_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج recall=recall_score(y_true, y_pred) # لطباعة الناتج كنسبة مئوية print(str(recall*100)+'%',sep='') # 75.0% # للتنويه: الرابط التالي يحوي شرح لمفاهيم TPو TN والبقية:

يعتبر من أهم معايير قياس دقة نماذج التصنيف Classification. وهو نسبة ماتوقعناه بشكل صحيح إلى مجموع التوقعات الكلية ويستخدم بكثرة، ويمكن التعبير عنه بالصيغة التالية: Accuracy = (TP+TN)/(TP+FP+FN+TN) الصيغة العامة للتابع الذي يقوم بحساب الدقة في مكتبة scikit-learn: sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True) حيث أن أول وثاني وسيط يمثلان القيم الحقيقية والمتوقعة على التوالي. الوسيط normalize في حال تم ضبطه على true يعيد قيمة عشرية تمثل الدقة (الحالة الافتراضية)، وفي حال ضبطه على False سيقوم بحساب TP+TN أي عدد التوقعات الصحيحة للنموذج. مثال: from sklearn.metrics import accuracy_score y_pred = [0, 1, 0, 1,0,1] # بفرض أن القيم المتوقعة كانت y_true = [0, 1, 0, 1,1,1] # بفرض أن القيم الحقيقية كانت # يكون الناتج print(accuracy_score(y_true, y_pred, normalize=True)) # 0.8333333333333334 # لطباعة الناتج كنسبة مئوية print(accuracy_score(y_true, y_pred)*100,'%',sep='') # 83.33333333333334% # تنويه: تجد شرح المفاهيم TP,TN,FP,FN في الرابط التالي بالتفصيل.

يتم ذلك باستخدام التابع التالي: sklearn.model_selection.train_test_split(data,label, test_size=None, train_size=None, random_state=None, shuffle=True) يقوم التابع train_test_split بتقسيم البيانات إلى عينات تدريب وعينات اختبار. data: تمثل مجموعة البيانات. label: تمثل الفئات (classes). test_size: لتحديد النسبة المئوية التي سيتم اقتطاعها من البيانات لاستخدامها كعينة اختبار. لو وضعنا 0.2، سيتم تخصيص 20% من البيانات للاستخدام كعينة اختبار. train_size: لتحديد النسبة المئوية التي سيتم اقتطاعها من البيانات لاستخدامها كعينة تدريب. random_state: هذا الوسيط غامض لدى الكثيرين. إنه يتحكم بطريقة الخلط المطبقة على البيانات أي لتحديد نظام العشوائية ويأخذ قيمة من النمط integer ويمكنك وضع أي قيمة تريدها، هذا الرقم يفهمه المترجم بطريقة معينة على أنه نمط معين للتقسيم. لنفهم فائدة هذا الوسيط سأعطيك المثال التالي: لنفرض أننا نعمل في فريق على مهمة تعلم آلة معينة. في حال لم نستخدم random_state سوف يتم تقسيم البيانات على جهاز كل عضو من الفريق بطريقة مختلفة، أما إذا اخترنا جميعاً قيمة ثابتة ولتكن 44 فهذا يعني أن البيانات ستقسم بنفس الطريقة على جهاز كل عضو، ولو أعدنا التقسيم 1000 مرة سيكون نفسه. وطريقة قسم البيانات مهمة فمثلاً إذا كانت عناصر مجموعة الاختبار a تختلف عن عناصر مجموعة الاختبار b، هذا سيؤدي إلى اختلاف ال score بين المجموعتين. shuffle: لعمل خلط للبيانات قبل تقسيمها (أي بعثرة أو إعادة ترتيب العينات بشكل عشوائي). في حال وضعنا False لن تتم البعثرة (يفضل وضعها True دوماً). الكود التالي يوضح العملية: # سنقوم بتحميل الداتاسيت الخاصة بأسعار المنازل في مدينة يوسطن ونقوم بتقسيمها import numpy as np from sklearn.model_selection import train_test_split from sklearn.datasets import load_boston # تحميل الداتاسيت BostonData = load_boston() data = BostonData.data label = BostonData.target # عرض حجم الداتا print('The shape of data:',data.shape,'\n') # The shape of data: (506, 13) أي لدينا 506 عينات # تقسيم الداتا X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.2, random_state=44, shuffle =True) # لاحظ أننا حددنا 20 بالمئة كعينة اختبار وبالتالي سيتم اعتبار الباقي عينة تدريب تلقائياً # عرض حجم البيانات بعد التقسيم print('The shape of X_train:',X_train.shape) # The shape of X_train: (354, 13) print('The shape of X_test:',X_test.shape) # The shape of X_test: (152, 13) print('The shape of y_train:',y_train.shape) # The shape of y_train: (354,) print('The shape of y_test:',y_test.shape) # The shape of y_test: (152,)

error matrix أو confusion_matrix: هي مصفوفة تستخدم لتقييم أداء نماذج التصنيف، أي نستخدمها عندما تكون المهمة هي مهمة تصنيف Classification. هذه المصفوفة تقوم بحساب TP و FP و FN و TN وترد مصفوفة تعبر عنهم بأبعاد (n_classes, n_classes). سأعطي مثال لشرحهم: تجري إحدى الكليات فحصاً لمرض كورونا باستخدام التعلم الآلي على جميع طلابها. الناتج إما مصاب بكورونا + أو سليم -. وبالتالي سيكون هناك 4 حالات من أجل طالب x. إذا كانت تبدأ بـ True، فإن التنبؤ كان صحيحاً سواء كان مصاباً بمرض كورونا أم لا. إذا كانت تبدأ بـ False، فإن التنبؤ كان غير صحيح. P تدل على الفئة الإيجابية و N السلبية، وهما خرج برنامجنا. True positive (TP): النموذج يتوقع أن الطالب x حالته + والطالب x هو فعلاً مصاب (وهذا جيد). أي توقع أن الشخص مصاب وهو مصاب فعلاً. True negative (TN): النموذج يتوقع أن الطالب x حالته - والطالب سليم (وهذا جيد). أي شخص سليم و تنبأ أنه سليم بشكل صحيح. False positive (FP): النموذج يتوقع أن الطالب x حالته + والطالب غير مصاب (وهذا سيئ). أي شخص سليم وتوقع أنه مصاب. False negative (FN): النموذج يتوقع أن الطالب x حالته - والطالب مصاب (وهذا الأسوأ). أي شخص مصاب وتوقع أنه سليم. لتطبيقها باستخدام مكتبة Sklearn نستدعي التابع confusion_matrix من الموديول metrics والمثال التالي يبين كل شيء: sklearn.metrics.confusion_matrix(y_true, y_pred, normalize=None) أول وسيطين يمثلان القيم الحقيقية والقيم المتوقعة، على التوالي. أما الوسيط الأخير فهو اختياري ويستعمل لعمل normalize للقيم وهو يأخذ 3 قيم: all: بالتالي يقسم كل قيم المصفوفة على مجموع كل التوقعات (جرب بنفسك). true: يقسم كل القيم في عمود j على مجموع القيم فيه. pred: يقسم كل القيم في سطر i على مجموع القيم فيه. لاستخراج قيم tp و tn و fp و fn من المصفوفة نستخدم التابع ()ravel مع ملاحظة أنه لايمكنك استخدام هذا التابع إلى في حالة أن التصنيف ثنائي. from sklearn.metrics import confusion_matrix y_true = ["cat", "dog", "cat", "cat", "dog", "dog","cat","cat"] y_pred = ["dog", "dog", "cat", "cat", "dog", "cat","cat","cat"] # حساب المصفوفة cm=confusion_matrix(y_true, y_pred,normalize=None') # عرض نتيجة المصفوفة print(cm) # لاستخراج القيم tp,fp,fn,tn=cm.ravel() #يمكنك التعبير عن هذه القيم بالرسم import matplotlib.pyplot as plt import seaborn as sea sea.heatmap(cm, center = True) plt.show()

اعتقد أنك تريد معرفة كيفية استدعاء الدوال الموجودة في الصف الابن والدوال الموجودة في الصف الاب من خلال الصف الابن؟ أليس كذلك؟ يمكنك القيام بذلك بشكل مباشر كالتالي: # تعريف الصف الأب class Person: def __init__(self,name,age): self.name=name self.age=age def get_age(self): # تابع يرد عمر الشخص return self.age # تعريف الصف الابن الذي يمثل طالب class Student(Person): def __init__(self,ID,name,age): self.ID=ID Person.__init__(self,name, age) def get_ID_and_name(self): return (str(self.ID)+" "+self.name) # تابع يرد رقم واسم الطالب # استدعاء الدوال الموجودة في الصف الابن stu = Student(55,'Ali',24) print(stu.get_ID_and_name()) # استدعاء الدوال الموجودة في الصف الاب من الصف الابن print(stu.get_age()) # ملاحظة : # نقوم باستدعاء باني الصف الاب داخل باني الصف الابن لكي نرث الخصائص الموجودة ضمن الدالة __init__ وبدون ذلك لن نكون قادرين على الوصول لل name و ال age أي لن تتم وراثتهما.

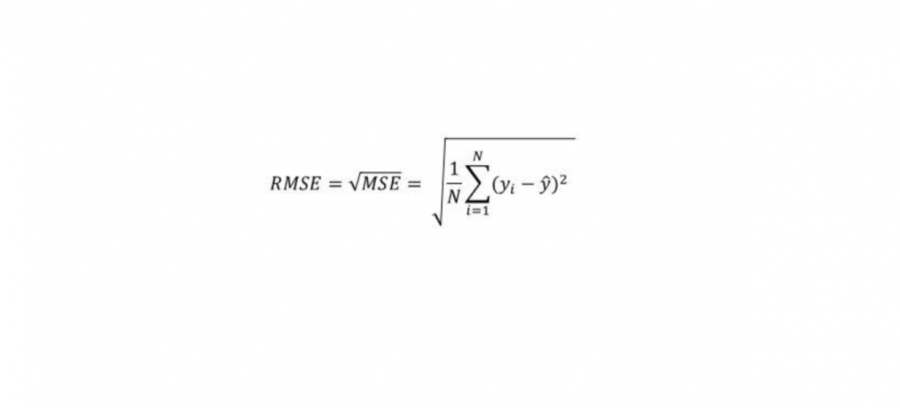
بشكل عام هناك 4 مقاييس أساسية لقياس كفاءة المودل عندما تكون المهمة من نوع Regrission (توقع): أول ورابع معيار هم الأكثر استخداماً. أولاً: Mean Absolute Error وهي متوسط الفروق بالقيمة المطلقة بين القيم الحقيقية والقيم المتوقعة في مجموعة البيانات، والصورة المرفقة في الأسفل توضح الشكل العام للمعادلة الرياضية المعبرة عنها. ثانياً: Mean Squared Error وهي متوسط مربع الفروق بين القيم الحقيقية والمتوقعة، في الأسفل تم توضيح الشكل الرياضي للمعادلة. ثالثاُ: Root Mean Squared Error وهو جذر ال Mean Squared Error، في الأسفل تم توضيح الشكل الرياضي للمعادلة. رابعاً: R Squared معايير القياس المذكورة أعلاه سيكون لها قيم مختلفة لنماذج مختلفة، أي ليس لها مجال ثابت لكي نخمن على أساسه هل النموذج جيد أم لا، فمثلاً في مشكلة توقع أسعار المنازل قد يكون مجال القيم لهما بين 100 و 400 دولار وفي مسألة توقع درجة الحرارة قد يكون المجال بين ال 1 و 4 (أي القيم الناتجة ليست سهلة القراءة)، أما في هذا المقياس فسوف يكون مجال القيم محصور بين ال 0 وال 1، بحيث 1 تعني أن النموذج خالي من الأخطاء و 0 تعني أن النموذج فاشل تماماً. في الصورة المرفقة في الأسفل تم توضيح الشكل الرياضي للمعادلة. مثال: # انتبه أن التابع mean_squared_error يقبل وسيط بولياني يسمى squared في حال ضبطه على True سيتم حساب MSE أما في حال ضبطه على False سوف يحسي MSE ثم يأخذ الجذر أي يصبح RMSE. ####################################### Example ############################################### # استيراد الدوال from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error from sklearn.metrics import r2_score y_true = [80.3, 100, -7.7] # نفرض أن القيم الحقيقية كانت y_pred = [85, 99, -0.5] # والقيم المتوقعة ####################################### MAE ################################################## print("MAE is: "+str(mean_absolute_error(y_true, y_pred))) # output: MAE is: 4.300000000000001 ####################################### MSE ################################################## print("MSE is:"+str(mean_squared_error(y_true, y_pred,squared=True))) # MSE is:24.976666666666677 ####################################### RMSE ################################################## print("RMSE is:"+str(mean_squared_error(y_true, y_pred,squared=False))) # RMSE is:4.997666121968001 ####################################### R Squaerd ################################################## print("R Squaerd is:"+str(r2_score(y_true, y_pred)))#R Squaerd is:0.9886074871600465 مثال واقعي على مهمة توقع أسعار المنازل في مدينة بوسطن، حيث أن البيانات تمثل مواصفات المنازل وأسعارها في تلك المدينة : ####################################### مثال عملي ################################################## from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error from sklearn.metrics import r2_score from sklearn.linear_model import LinearRegression # تحميل الداتاسيت BostonData = load_boston() x = BostonData.data y = BostonData.target # تقسيم الداتا إلى عينة تدريب وعينة اختبار X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=44, shuffle =True) #تعريف LinearRegressionModel LR = LinearRegression() LR.fit(X_train, y_train) # حساب القيم المتوقعة y_pred = LR.predict(X_test) # Mean Absolute Error MAE = mean_absolute_error(y_test, y_pred) print('Mean Absolute Error Value is : ', MAE) #Mean Absolute Error Value is : 3.4318693222761523 # Mean Squared Error MSE = mean_squared_error(y_test, y_pred,squared=True) print('Mean Squared Error Value is : ', MSE) #Mean Squared Error Value is : 21.439149523649792 # Root Mean Squared Error RMSE = mean_squared_error(y_test, y_pred,squared=False) print('Root Mean Squared Error Value is : ', RMSE) #Root Mean Squared Error Value is : 4.6302429227471205 # R Squaerd print("R Squaerd is: "+str(r2_score(y_test, y_pred))) # R Squaerd is: 0.7532417995961468 فرانسوا كوليت ينصح باعتماد MAE.

اعتقد أنك تقصد كيفية إنشاء قائمة من الكائنات. # تعريف صف class hsoub: def __init__(self, name, ID): self.name = name self.ID = ID list = [] # إنشاء قائمة # إضافة كائنات إلى الصف list.append( hsoub('Ali', 9) ) list.append( hsoub('Ahmad', 6) ) list.append( hsoub('Mohameed', 8) ) # طباعة for object in list: print( object.name, object.ID ) هل تريد شيئاً إضافياً؟

dic1={'team1':5, 'lose1':39} dic2={'team2':3, 'lose2':40} def combine(f1, f2): dic = f1.copy() #dic ننشئ نسخة من القاموس الأول ونسميها dic.update(f2) # نضيف لهذا القاموس مفاتيح وقيم القاموس الثاني return dic combine(dic1, dic2) ''' في حال كانت إحدى المفاتيح في القاموس الأول موجودة في الثاني فسيتم استبدالها بمفاتيح الثاني ''' ويمكن أن تجرب: dic = dict(list(dic1.items()) + list(dic2.items())) حيث items هي تابع يرد المفاتيح والقيم في أول قاموس وتضعهم على شكل list من ال tuble ثم تدمجهما مع الثانية وتحولهما في النهاية إلى قاموس في النسخ الحديثة من بايثون يمكنك أن تفعل هذا ببساطة : dic = {**dic1, **dic2}

# + لدمج قائمتين نستخدم المعامل # مثلاً list1=[5,5,8] list2=[5,99,8] list=list1+list2

f=[ {'team':'barca', 'lose':39}, {'team':'real', 'lose':40}, {'team':'ATM', 'lose':10}] from operator import itemgetter f = sorted(f, key=itemgetter('lose'),reverse=True) # سيكون الترتيب من الأصغر للأكبر False إذا وضعت print(f)

def count(text): tokens = [] # لتخزين الكلمات في النص بدون تكرار text = text.split() # لتقسيم النص إلى كلمات for word in text: # نمر على كل كلمة بالنص if word not in tokens: # إذا لم تكن الكلمة موجودة مسبقاً نضيفها tokens.append(word) for word in range(0, len(tokens)): #count نمر على كل كلمة فريدة بالنص ونحسب تكرارها باستخدام التابع print(tokens[word], ': ', text.count(tokens[word])) s ='Ali Messi Ali Messi Real Messi FCB FCB' count(s) # استدعاءالتابع

جرب: #!/usr/bin/env -S python3 -u

import re # regex استيراد المكتبة txt = input() # إدخال النص result = re.findall("\d*\.*\d* [E|e]uros", txt) # عرض النتائج if result: for word in result: print(word) else: print("No Euros!") يجب أن تكون الآن قادر على كتابة باقي الأكواد وحدك!

import re # regex استيراد المكتبة txt = input() # إدخال النص result = re.findall("056\d{7}", txt) # أي أول 3 محارف يجب أن يكونوا056 وبعدها 7 أرقام # عرض النتائج if result: for word in result: print(word) else: print("No ID!") الرمز d\ يدل على وجود رقم الرمز {7} يدل على أن المحرف الموجود قبلها يجب أن يتكرر 7 مرات وفي حالتنا (d\ أي يجب أن يتواجد 7 أرقام) الدالة (pattern,string)findall تبحث في النص الذي نمرره له مكان الباراميتر string لترى ما إذا كان يتطابق أو فيه جزء يتطابق مع التعبير النمطي الذي نمرره لها مكان الباراميتر pattern. في حال تم إيجاد جزء أو أكثر في النص يتطابق مع التعبير النمطي, ترجع list كل عنصر فيه يمثل الجزء الذي يتطابق مع التعبير النمطي. في حال لم يتم إيجاد أي تطابق, ترجع list فارغ. # تعدييييييل: الرمز ^ يختبر فقط بداية النص أي سيختبر مطابقة ال pattern مع أول كلمة في ال string لذلك لايصلح لاستخدامه في هذه المهمة وبشكل مشابه أيضاً المحرف $.

import re # regex استيراد المكتبة txt = input() # إدخال النص # $إيجاد كل مايبدأ بالرمز # وبعده رقم واحد على الأقل result = re.findall("\$\d+", txt) # عرض النتائج if result: for word in result: print(word) else: print("No dollars!")

model.save('our_model.hdf5') # 'my_model.hdf5' هنا قمنا بحفظ النموذج في ملف # المسار المطلوب تخزينه فيه save أي نمرر للدالة from keras.models import load_model # لتحميل المودل بعد أن قمنا بتخزينه model = load_model('our_model.hdf5') طبعاً يمكنك حفظ نموذجك بصيغ أخرى مثل h5 أو Json.. لكن شخصياً أنصح ب hdf5.