البحث في الموقع

تستخدم منحنيات بيزيه Bezier curves في رسوميات الحاسوب لإنشاء الأشكال والرسوم المتحركة المعتمدة على أوراق التنسيق المتتالية CSS وغيرها. هذه المنحنيات بسيطة وتستحق الدراسة، وبعدها ستكون مرتاحًا عند التعامل مع الرسوميات الشعاعية vector graphics والرسوم المتحركة المتقدمة. نقاط التحكم يحدد منحني بيزيه بواسطة مجموعة من النقاط الحاكمة، وقد يكون عددها 2 أو 3 أو 4 أو أكثر، لاحظ مثلًا منحنيًا من نقطتين: والمنحني التالي محدد بثلاث نقاط: وهذا بأربع نقاط: لو تمعنت في هذه المنحنيات، فيمكنك أن تلاحظ التالي: لا تنتمي النقاط بالضرورة إلى المنحني وهذا أمر طبيعي، وستفهم ذلك عندما سنشرح طريقة بنائه لاحقًا. درجة المنحني curve order تساوي عدد النقاط ناقصًا واحدًا، فالمنحني المؤلف من نقطتين هو خط مستقيم من الدرجة الأولى، والمنحني المؤلف من ثلاث نقاط هو منحن تربيعي، أي قطع مكافئ، وهكذا. ينحصر المنحني ضمن المضلع المحدّب convex hull الذي تشكله النقاط الحاكمة: سنتمكن من أَمثَلة اختبارات التداخل في رسوميات الحاسوب اعتمادًا على الخاصية الأخيرة، فلن تتداخل المنحنيات إن لم تتداخل المضلعات المحدبة، وبالتالي ستعطي دراسة تداخل المضلعات المحدبة جوابًا سريعًا لتداخل المنحنيات، بالإضافة إلى أنّ دراسة تداخل المضلعات أسهل لأنّ أشكالها مثل المثلث والمربع، تُعَد مفهومة موازنةً بالمنحنيات. تكمن الفائدة الرئيسية لاستخدام منحني بيزيه في تغيير شكل المنحني بمجرد تحريك النقاط الحاكمة. لاحظ المنحني الذي تولده الشيفرة التالية، واستخدم الفأرة لتحريك النقاط الحاكمة وراقب تغير المنحني: ستتمكن بعد التمرن قليلًا من رسم المنحني المطلوب بمجرد تحريك النقاط الحاكمة، ويمكنك عمليًا الحصول على أي شكل تريده بوصل عدة منحنيات، إليك بعض الأمثلة: خوارزمية دي كاستلجو De Casteljau يمكننا استخدام صيغة رياضية لرسم منحنيات بيزيه، وهذا ما سنشرحه لاحقًا، لأنّ خوارزمية دي كاستلجو De Casteljau’s algorithm التي نسبت لمخترعها، تتطابق مع التعريف الرياضي، وتساعدنا على تمييز طريقة إنشاء المنحنيات بصريًا. سنرى أولًا مثالًا لمنحن من ثلاث نقاط حاكمة، لاحظ أنه يمكنك تحريك النقاط 1 و 2 و 3 بالفأرة، ثم انقر زر التشغيل الأخضر. خوازمية دي كاستلجو لبناء منحني بيزيه من ثلاث نقاط ارسم النقاط الثلاث، والتي تمثلها النقاط 1 و2 و3 في المثال السابق. صل بين النقاط السابقة باتجاه واحد 3 → 2 → 1، وهي الخطوط البنية في المثال السابق. يأخذ المعامل t قيمه بين "0" و"1"، وقد استخدمنا في مثالنا النموذجي السابق خطوةً مقدارها "0.05"، أي تتحرك حلقة التنفيذ وفق الآتي: 0 ثم 0.05 ثم 0.1 ثم 0.15 وهكذا. لكل قيمة من قيم t: نأخذ على كل خط بني بين نقطتين متتاليتين نقطةً تبعد عن بدايته مسافةً تتناسب مع t، وطالما أن هناك خطان، فسنحصل على نقطتين، وستكون كلتا النقطتين في بداية الخط عندما يكون t=0 مثلًا، كما ستبعد النقطة الأولى عن بداية الخط مسافةً تعادل 25% من طوله عندما تكون t=0.25، وهكذا. نصل بين النقطتين المتشكلتين، والخط الواصل في المثال التالي باللون الأزرق. table { width: 100%; } thead { vertical-align: middle; text-align: center; } td, th { border: 1px solid #dddddd; text-align: right; padding: 8px; text-align: inherit; } tr:nth-child(even) { background-color: #dddddd; } p iframe.code-result__iframe { border: 1px solid #e7e5e3 !important; } t=0.25 t=0.5 خذ على الخط الأزرق السابق نقطةً تبعد عن طرفه مقدارًا يتناسب مع t، ستكون النقطة في نهاية الربع الأخير من الخط من أجل t=0.25، وستكون في منتصف الخط من أجل t=0.5، وهي النقطة الحمراء في الشكل السابق. عندما تتحول t بين 0 و1 ستضيف كل قيمة لهذا المعامل نقطةً من نقاط المنحني، وتمثل هذه المجموعة من النقاط منحني بيزيه. نتبع الأسلوب ذاته بالنسبة لمنحنى مكون من أربع نقاط حاكمة. الخوارزمية المتبعة لأربع نقاط هي: صل بين النقاط الحاكمة 1 إلى 2، و2 إلى 3، و3 إلى 4، وستحصل على ثلاثة خطوط بنية. لكل قيمة للمعامل t بين 0 و1: نأخذ نقاطًا على الخطوط الثلاثة تتناسب مع t كما فعلنا سابقًا، وبوصل هذه النقاط الثلاثة المتشكلة سنحصل على خطين جديدين، باللون الأخضر مثلًا. نأخذ على الخطين الأخضرين نقاطًا متناسبةً مع t، وعندها سنصل بين النقطتين المتشكلتين فنحصل على خط واحد، وليكن باللون الأزرق. نأخذ على الخط الأزرق نقطةً تبعد عن أحد طرفي الخط مسافةً متناسبةً مع t، فنحصل على نقطة حمراء واحدة تمثل أحد نقاط منحني بيزيه. تمثل النقاط الحمراء كلها المنحني الكامل. إن الخوارزمية السابقية تعاودية، أي قادرة على إعادة نفسها، لذلك يمكن تعميمها إلى N نقطة حاكمة: نصل بين النقاط فنحصل على N-1 خطًا. لكل قيمة للمعامل t بين 0 و1 نأخذ على كل خط نقطةً تبعد عن طرف الخط مسافةً متناسبةً مع t، ونصل بين هذه النقاط فنحصل على N-2 خطًا. نكرر الخطوة 2 حتى نحصل على نقطة واحدة تمثل إحدى نقاط منحني بيزيه. تشكل جميع النقاط الناتجة في الخطوة 3 منحني بيزيه. شغّل الرسوميات التالية ولاحظ شكل المنحني: منحن يبدو مثل الخط البياني للدالة y=1/t. نقاط حاكمة بشكل Zig-zag تبدو جيدةً أيضًا: يمكن رسم حلقة: يمكن رسم منحني بيزيه غير أملس أيضًا: تابع الأمثلة الحية السابقة لترى كيف يُبنى المنحني، إذا وجدت شيئًا مبهمًا في وصف الخوارزمية. يمكن استخدام العدد الذي نريده من النقاط الحاكمة لرسم منحني بيزيه من أي درجة، ما دامت الخوارزمية تعاوديةً، لكن يفضل عمليًا استخدام عدد قليل من النقاط -عادةً 2 أو 3 نقاط-، ثم نربط بين عدة منحنيات بسيطة إذا أردنا شكلًا أكثر تعقيدًا. الصيغ الرياضية يمكن توصيف منحني بيزيه باستخدام صيغة رياضية، وكما رأينا فلا حاجة لمعرفة هذه الصيغة. يرسم المستخدمون المنحني بمجرد تحريك النقاط بالفأرة، لكن إذا أردت استخدام الرياضيات فلك هذا. لنفترض أنّ إحداثيي نقطة حاكمة هو Pi. ستكون النقطة الأولى (P1 = (x1, y1، والثانية (P2 = (x2, y2، وهكذا حتى آخر نقطة (Pi = (xi, yi، ويمكن أن نصف منحني بيزيه بمعادلة متغيرها t يأخذ قيمه بين 0 و1. صيغة منحن يمر بنقطتين هي: صيغة منحن يمر من 3 نقاط هي: صيغة منحن يمر من 4 نقاط هي: إنّ المعادلات السابقة هي معادلات شعاعية، أي يمكننا وضع الإحداثيين x وy بدلًا من P، فمن أجل المنحني المار من ثلاث نقاط مثلًا ستصبح الصيغة بدلالة x وy هي: ينبغي تعويض القيم x1, y1, x2, y2, x3, y3 في المعادلات وكتابة الصيغة بدلالة المتغير t، فلو فرضنا أنّ إحداثيات النقاط الحاكمة الثلاثة هي: (0,0) و(0.5, 1) و(1, 0)،فستصبح قيمة إحداثيي النقطة المقابلة من منحني بيزيه: سنحصل على إحداثيي نقطة جديدة (x,y) من نقاط منحني بيزيه كلما تغيرت قيمة t بين 0 و1. خلاصة تُحدَّد منحنيات بيزيه بثلاث نقاط حاكمة، ويمكن رسمها بأسلوبين كما رأينا: باستخدام عملية رسومية: أي خوارزمية دي كاستلجو. باستخدام صيغة رياضية. من الصفات الجيدة لمنحنيات بيزيه: إمكانية رسم منحنيات ملساء عبر تحريك النقاط الحاكمة باستخدام الفأرة. إمكانية رسم أشكال أكثر تعقيدًا بوصل عدة منحنيات بيزيه معًا. استخدامات منحنيات بيزيه: في رسوميات الحاسوب والنمذجة ومحررات الرسوميات الشعاعية، كما توصف بها أنواع خطوط الكتابة. في تطوير تطبيقات الويب، من خلال الرسم ضمن لوحات وفي الملفات بتنسيق SVG، وقد كتبت الأمثلة النموذجية السابقة بتنسيق SVG، وهي عمليًا مستند SVG مفرد أُعطي نقاطًا مختلفةً مثل معاملات، ويمكن فتح هذه النماذج في نوافذ منفصلة والاطلاع على الشيفرة المصدرية: demo.svg. في الرسوميات المتحركة لوصف مسارها وسرعتها. ترجمة -وبتصرف- للفصل Bezier curve من سلسلة The Modern JavaScript Tutorial. اقرأ أيضًا المقال السابق: كائنا localStorage وsessionStorage لتخزين بيانات الويب في جافاسكربت أساسيات منحنى بيزيه Bezier Curve في سكريبوس تأثيرات الانتقال والحركة في CSS

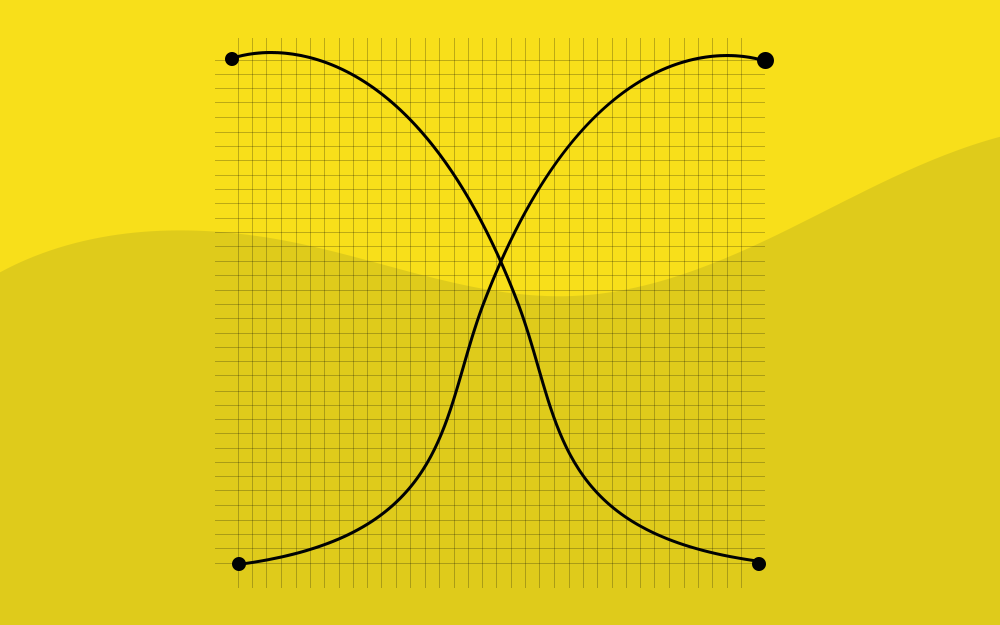
ربما استخدمت سابقًا أداة منحنى بيزيه Bezier Curve في برنامج سكريبوس Scribus لإنشاء بعض المنحنيات الجميلة، ولكن يُرجَّح أنك كنت مرتبكًا تمامًا ولم تتمكن من إنشاء أي شيء بخلاف بعض المنحنيات العشوائية. يُظهِر الشكل التالي محاولةً أولى في إنشاء دائرة باستخدام أداة منحنى بيزيه دون فهمها أولًا. إذا كانت محاولاتك لاستخدام هذه الأداة مشابهةً للشكل السابق، فهذا المقال يناسبك. الإعداد افتح برنامج سكريبوس وأنشئ مستندًا جديدًا (سيفي القياس A4 أو رسالة Letter بالاتجاه الرأسي بالغرض). يجب أولًا أن تُظهِر الشبكة وتفعّل خاصية اتباع الشبكة Grid Snapping -وهذا مهم لأنه سيسمح لك بإنشاء الأشكال بسهولة أكبر-، باتباع الآتي: اختر قائمة ملف File ثم إعداد المستند Document Setup. حدد قسم "الأدلة Guides" من القائمة. حدّد الخيار شبكة الصفحة Page Grid لإظهارها من تبويب الوضوح. اضبط تباعد الشبكة الرئيسية Major Grid Spacing على القيمة 100 نقطة. اضبط تباعد الشبكة الثانوية Minor Grid Spacing على القيمة 20 نقطة. اضغط على موافق. اختر قائمة صفحة Page ثم اتبع الشبكة Snap to Grid. إذا كان الخيار "اتبع الشبكة" محدَّدًا مسبقًا، فلا تحدده مرةً أخرى. يجب أن يبدو مستندك كالشكل التالي: إنشاء المنحنى الأول من الأشياء المهمة التي يجب معرفتها حول استخدام منحنيات بيزيه، أنه لا يمكنك إنشاء جميع الأشكال الممكنة دفعةً واحدة، إذ تتبع أداة منحنى بيزيه قواعدًا معينةً عند الرسم بها، لذلك يجب عدم تجربة إنشاء أشكال خيالية أو معقدة للغاية. سنتبع في هذا المقال بعض الاصطلاحات التي تسهّل توضيح ما عليك تطبيقه باستخدام الرسوم البيانية كما في الشكل التالي: تشير إشارة X الحمراء إلى النقطة التي تحتاج فيها إلى النقر بزر الفأرة الأيسر ثم تحريره (نقرة عادية فقط). يشير السهم الأزرق إلى أنه يجب عليك الضغط بزر الفأرة الأيسر على نهاية السهم عند النقطة، والاستمرار في الضغط على زر الفأرة، ثم سحب المؤشر حتى تصل إلى النهاية عند رأس السهم حيث يجب تحرير زر الفأرة بعد ذلك. يشير المربع الأصفر إلى أنه يجب النقر بزر الفأرة الأيمن لإنهاء رسم المنحنى، ولا يهم مكان مؤشر الفأرة عند النقر بزرها الأيمن. تمثل الأرقام الموجودة بجانب الأشكال الترتيب الذي يجب أن تطبّق به هذه الإجراءات. يمكنك إنشاء المنحنى الأول باستخدام الخطوات التالية الموضّحة في الشكل السابق: الإجراء الأول هو النقر على الزاوية اليسرى السفلية من المربع. ثم اسحب من أعلى اليمين إلى أعلى اليسار. ثم انقر بزر الفأرة الأيمن للانتهاء. يمكنك الآن تجربة الخطوات السابقة كما يلي: اختر قائمة إدراج Insert ثم منحنى بيزيه، أو يمكنك تحديد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضّحة في الشكل السابق. يجب أن يكون لديك الآن قوس بسيط أو ربع دائرة مثل الشكل التالي: الشيء الذي طبّقته حتى الآن هو إخبار سكريبوس بمكان بدء رسم المنحنى (النقطة 1)، وبالمكان الذي سيمر المنحنى من خلاله (النقطة 2)، وتشير النقطة 3 إلى الطريقة التي تريد رسم المنحنى بها. يستخدم سكريبوس أثناء رسم المنحنيات أشياءً تسمى نقاط التحكم Control Points تخبره بكيفية تشكيل المنحنى، فنقطة التحكم الوحيدة في هذا المثال هي الموضع 3 (نهاية السحب). إنشاء منحنى كامل سترسم الآن منحنيًا كاملًا وستبدأ الأمور في أن تصبح أوضح قليلًا، وهنا اتبع الآتي: اختر قائمة إدراج ثم منحنى بيزيه، أو يمكنك تحديد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضحة في الشكل التالي: يجب أن تنشأ لديك نصف دائرة مثل الشكل التالي: ربما لاحظت تحرّك "النهاية الحرة" للمنحنى مع مؤشر الفأرة مثل الخط المنقّط في الشكل الآتي، لأن سكريبوس يحاول باستمرار حساب المكان الذي يجب رسم الجزء الأخير من المنحنى فيه، كما أن المنحنى يتبع دائمًا بعض الاتجاهات المختارة مسبقًا بغض النظر عن المكان الذي حرّكتَ مؤشر الفأرة فيه، وسبب ذلك هو نقاط التحكم. انقر نقرًا مزدوجًا على نصف الدائرة الذي أنشأته للتو لتفتح نافذة محرر العقد Node Editor. يوضَح الشكل الآتي كيفية إنشاء منحنى نصف الدائرة، حيث يمكنك أن ترى في أسفل اليسار المكان الذي نقرت عليه لبدء المنحنى (مكان تواجد النقطة الزرقاء) والذي يُسمى عقدة Node، فالعقدة هي ببساطة نقطة يرسم سكريبوس منحنى من خلالها. يمكنك أيضًا أن ترى في الجزء العلوي مكان السحب من موضع إلى آخر، حيث أنشأت بداية السحب العقدة الثانية، كما أنشأت نهاية السحب نقطةً وردية اللون (النقطة A)، والتي تُسمَّى نقطة تحكم. تخبر نقاط التحكم سكريبوس بكيفية رسم المنحنى من خلال النقاط (العقد) الأخرى التي اخترتها. يمكنك رؤية العقدة الأخيرة في أسفل اليمين، ولكن هناك أيضًا نقطة تحكم وردية أخرى لم تنشئها (النقطة B)، وإنما أنشأها سكريبوس، وهي النقطة المضاعفة والمقابلة لنقطة التحكم الأولى. لقد أخبرتَ سكريبوس بمكان إنشاء نقطة التحكم الأولى عندما سحبت من النقطة 2 إلى النقطة 3، ولكنك أيضًا منحته -من خلال اتجاه السحب- اتجاهًا يعكس فيه نقطة التحكم الأولى عبر العقدة الثانية لإنشاء نقطة التحكم الثانية، وقد حدث هذا الانعكاس بزاوية قائمة على "الخط" الذي رسمته بالسحب من النقطة 2 إلى النقطة 3. لاحظ الخط المنقّط الأرجواني في الشكل التالي: يستغرق هذا المفهوم بعض الوقت للتعود عليه وأفضل طريقة لفهمه هي التدرب على رسم بعض المنحنيات مع السحب من النقطة 2 إلى النقطة 3 بزوايا مختلفة. حاول إنشاء مزيد من المنحنيات مع تغيير زاوية السحب، ثم افتح محرّر العقد لمعرفة مكان إنشاء نقاط التحكم، حيث يمكنك بعد ذلك تجربة بعض المنحنيات الأكثر تعقيدًا. أغلق نافذة محرّر العقد بالضغط على إنهاء التحرير أو على موافق عند الانتهاء. إنشاء دائرة كاملة اختر قائمة إدراج ثم منحنى بيزيه، أو حدد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضّحة في الشكل التالي: يجب أن تحصل الآن على دائرة مشابهة للشكل التالي: لاحظ تغيير اتجاه المنحنى الثاني من خلال السحب في اتجاه مختلف في المرة الثانية، إذ يمكنك الذهاب في أي اتجاه تريده بمجرد الانتهاء من منحنى كامل. إنشاء موجة سنرسم هذه المرة خطًا متموجًا، وذلك باتباع الخطوات الآتية: اختر قائمة إدراج ثم منحنى بيزيه، أو حدّد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضَّحة في الشكل التالي: يجب أن تحصل الآن على شكل يشبه الشكل التالي: لاحظ كيف يمكنك تغيير اتجاه المنحنى. إنشاء شكل الشبح اختر قائمة إدراج ثم منحنى بيزيه، أو حدّد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضّحة في الشكل الآتي، أينما حذفنا الأرقام من أسفل الرسم البياني لمنع حدوث فوضى، ولكن يجب أن تكون قادرًا على تحديد الطريق الذي يجب أن تسلكه. يمكنك بعد ذلك إعطاء الشبح لون تعبئة، ورسم بعض العيون باستخدام الدوائر، وستحصل على شكل شبيه بالشكل الآتي (بؤبؤ العين عبارة عن نسخٍ أصغر من بياض العين). لا تقلق إن لم تتمكن من رسم الشبح بالكامل، فهذا ليس مهمًا حاليًا، لأن المهم هو معرفة كيفية رسم المنحنيات. يمكنك استخدام هذه التقنيات البسيطة جدًا التي تعلمتّها لصنع الأشكال بسهولة. إنشاء أشكال مفيدة يمكنك باستخدام منحنى بيزيه رسم دوائر، ولكن سكريبوس لديه أداة لرسم الدوائر فعليًا بحيث يمكنك رسم شبح بها، ولكن قد تتساءل عن فائدة رسم مثل هذه الأشكال عمليًا، فالأشكال التي رسمتها حتى الآن لا تُعَد مفيدةً جدًا، لكنها تُظهِر لك كيفية عملية الرسم. إذًا لنرسم الآن بعض الأشياء المفيدة. إنشاء مستطيلات ذات زوايا منحنية تُعَد المستطيلات ذات الزوايا المنحنية مفيدةً للغاية، ويمكنك إنشاؤها عن طريق رسم شكل مستطيل عادي واستخدام خاصية التدوير في سكريبوس (من تبويب شكل Shape في نافذة الخصائص Properties)، ولكن يمكنك أيضًا رسم منحنياتك الخاصة باستخدام منحنيات بيزيه. اختر قائمة إدراج Insert ثم منحنى بيزيه، أو حدد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضّحة في الشكل التالي: يجب أن تحصل الآن على شكل يشبه الشكل التالي: لننشئ الآن أشكالًا أكثر تعقيدًا. إنشاء أشكال ذات زوايا منحنية يمكنك رسم أي شكل له زوايا منحنية تقريبًا باستخدام منحنيات بيزيه، وذلك باتباع الآتي: اختر قائمة إدراج ثم منحنى بيزيه، أو حدد أداة منحنى بيزيه من شريط الأدوات. اتبع الإجراءات الموضَّحة في الشكل الآتي، وابدأ من النقطة S (البداية)، ثم تحرّك باتجاه عقارب الساعة إلى النقطة E (النهاية) كما يلي: ثم يجب أن تحصل على الشكل التالي: تمرين حاول إنشاء الأشكال الموضَّحة في الشكل الآتي للمتعة فقط، إذ يمكنك إنشاء أي شكل تريده باستخدام منحنى بيزيه واحد والتقنيات الموضحة سابقًا. ترجمة -وبتصرّف- للمقال Bezier Curve Basics - Part 1 - Simple Geometric Shapes. اقرأ أيضًا خط الشبكة الأساسي Baseline Grid في برنامج سكريبوس كيف تعزل صورة وتنشئ مسار قطع Clipping Path لتدفق النص في سكريبوس كيفية إنشاء رمز RSS Feed في برنامج سكريبوس Scribus كيفية إنشاء التأثير Distressing Mask في برنامج سكريبوس لإنتاج تأثيرات تعبئة جذابة كيفية إنشاء الظلال في برنامج سكريبوس Scribus